湘教版数学九年级上册 复习课件:3.4《三角形全等的判定》(共19张PPT)
文档属性
| 名称 | 湘教版数学九年级上册 复习课件:3.4《三角形全等的判定》(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 346.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 00:00:00 | ||
图片预览



文档简介
课件19张PPT。湘教版数学八年级上册
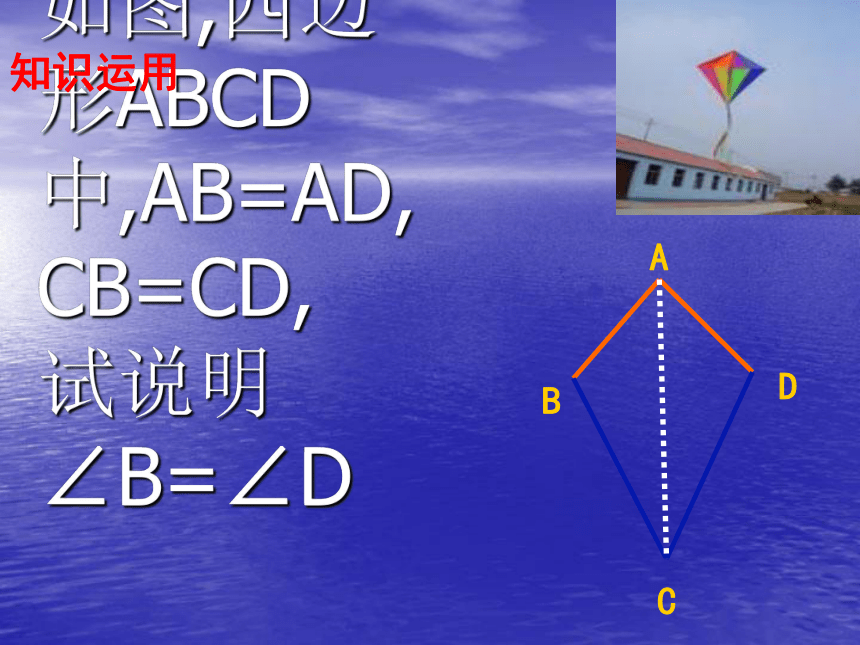
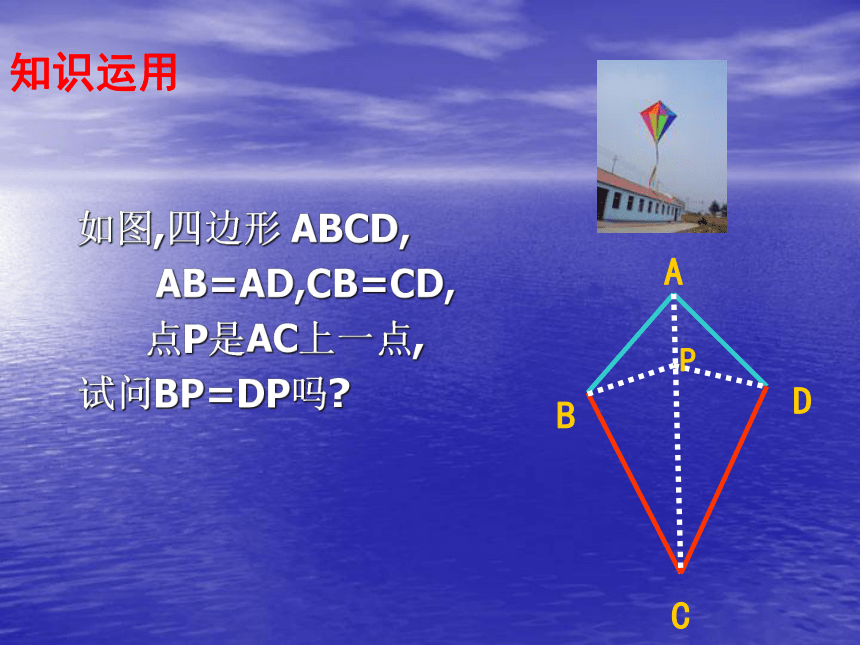
三角形全等判定的复习课回顾到现在为止,你能够用几种方法说明两个三角形全等?答:有五种:SAS、ASA、AAS、SSS、HL如图,四边形ABCD中,AB=AD,CB=CD, 试说明 ∠B=∠D知识运用如图,四边形 ABCD,
AB=AD,CB=CD,
点P是AC上一点,
试问BP=DP吗?P知识运用ACEBFD如图,AC=AD,CE=DF, ∠C =∠D , BE=BF
试说明
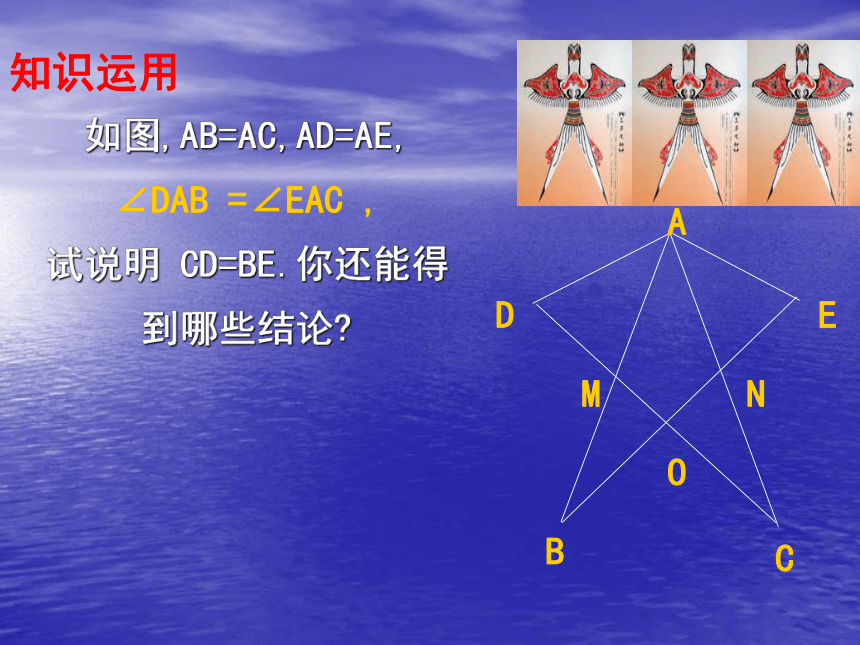
AB平分∠EBF知识运用ABCDEMN如图,AB=AC,AD=AE, ∠DAB =∠EAC ,
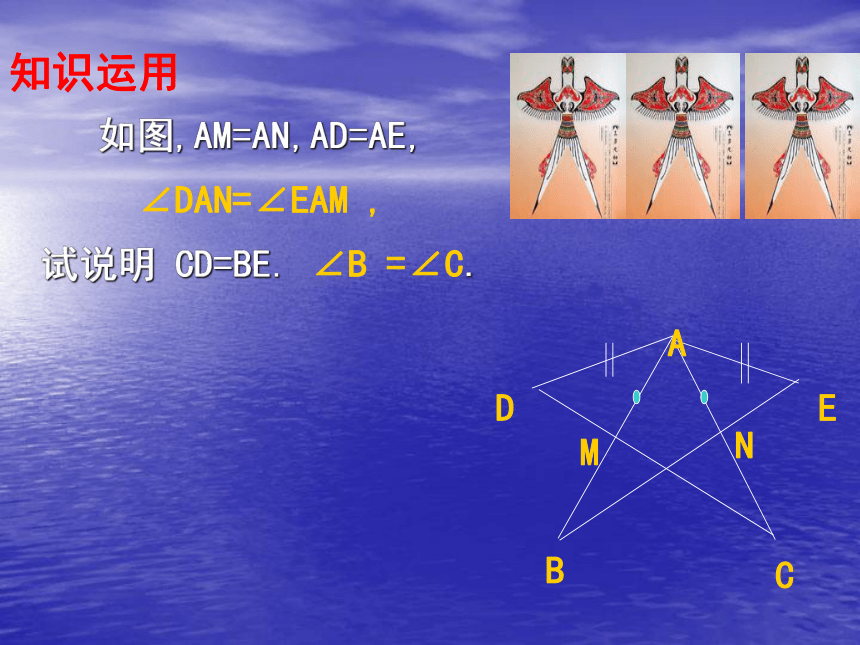
试说明 CD=BE.你还能得到哪些结论?O知识运用如图,AM=AN,AD=AE, ∠DAN=∠EAM ,
试说明 CD=BE. ∠B =∠C.知识运用如图,AB⊥AE,AC ⊥AD,
AD=AE,CD=BE
试说明 ∠B =∠C.
你还能得到哪些结论?知识运用如图,AB=AC,AD是BC边上的中线, 试说明AD平分∠BAC,知识运用1.如图,AB=AC, AD平分∠BAC 试说明AD是BC边上的中线
2.如图,AB=AC, AD平分∠BAC 试说明AD垂直平分BC.
3.如图, AD垂直平分BC
试说明AB=AC, AD平分∠BAC.
4.如图,AB=AC, AD⊥BC 试说明AD平分∠BAC.
D一题多变5.如图,AB=AC, 你会说明∠B=∠C吗?
作AD⊥BC ,垂足是D.或作∠BAC平分线,或作BC边上的中线.6.如图, ∠B=∠C 你会说明AB=AC, 吗?
拓展与提高1.如图,AB=AC, AD是BC边上的中线 P是AD 的一点,试说明PB=PC
2.如图,AB=AC, AD平分∠BAC.
BE=CF,试说明DE=DF
拓展与提高ABC3.如图,AB=AC, AD平分∠BAC,P是AD 的任意一点,试说明PB=PC总能成立吗?
DP拓展与提高O4.如图,AB=AC, BD=CD
试说明AD垂直平分BC.拓展与提高 如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。解:BD=CD
因为∠ADB=∠ADC=90°
AB=AC
AD=AD所以Rt△ABD≌Rt△ACD(HL)
所以BD=CD活动和探索例:已知:A B⊥AC,CD ⊥AC,AD=CB, 问△ABC 与△CDA全等吗?为什么?∵AD=CB(已知)
AC=CA(公共边)∴Rt△ABD≌Rt△ACD(HL) ∵ A B⊥AC,CD ⊥AC∴∠1=∠2=90°答:△ABC ≌ △CDA活动和探索 如图,∠ACB=∠BDA=90°。要说明△ACB≌△BDA,需要再补充几个条件,
应补充什么条件?把它们分别写出来,
有几种不同的方法就写几种。 活动和探索小结:这节课你有什么收获呢?与你的同伴进行交流你觉得在平时的学习中注意归纳与总结对学好几何有帮助吗?再 见
三角形全等判定的复习课回顾到现在为止,你能够用几种方法说明两个三角形全等?答:有五种:SAS、ASA、AAS、SSS、HL如图,四边形ABCD中,AB=AD,CB=CD, 试说明 ∠B=∠D知识运用如图,四边形 ABCD,
AB=AD,CB=CD,
点P是AC上一点,
试问BP=DP吗?P知识运用ACEBFD如图,AC=AD,CE=DF, ∠C =∠D , BE=BF
试说明
AB平分∠EBF知识运用ABCDEMN如图,AB=AC,AD=AE, ∠DAB =∠EAC ,
试说明 CD=BE.你还能得到哪些结论?O知识运用如图,AM=AN,AD=AE, ∠DAN=∠EAM ,
试说明 CD=BE. ∠B =∠C.知识运用如图,AB⊥AE,AC ⊥AD,
AD=AE,CD=BE
试说明 ∠B =∠C.
你还能得到哪些结论?知识运用如图,AB=AC,AD是BC边上的中线, 试说明AD平分∠BAC,知识运用1.如图,AB=AC, AD平分∠BAC 试说明AD是BC边上的中线
2.如图,AB=AC, AD平分∠BAC 试说明AD垂直平分BC.
3.如图, AD垂直平分BC
试说明AB=AC, AD平分∠BAC.
4.如图,AB=AC, AD⊥BC 试说明AD平分∠BAC.
D一题多变5.如图,AB=AC, 你会说明∠B=∠C吗?
作AD⊥BC ,垂足是D.或作∠BAC平分线,或作BC边上的中线.6.如图, ∠B=∠C 你会说明AB=AC, 吗?
拓展与提高1.如图,AB=AC, AD是BC边上的中线 P是AD 的一点,试说明PB=PC
2.如图,AB=AC, AD平分∠BAC.
BE=CF,试说明DE=DF
拓展与提高ABC3.如图,AB=AC, AD平分∠BAC,P是AD 的任意一点,试说明PB=PC总能成立吗?
DP拓展与提高O4.如图,AB=AC, BD=CD
试说明AD垂直平分BC.拓展与提高 如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。解:BD=CD
因为∠ADB=∠ADC=90°
AB=AC
AD=AD所以Rt△ABD≌Rt△ACD(HL)
所以BD=CD活动和探索例:已知:A B⊥AC,CD ⊥AC,AD=CB, 问△ABC 与△CDA全等吗?为什么?∵AD=CB(已知)
AC=CA(公共边)∴Rt△ABD≌Rt△ACD(HL) ∵ A B⊥AC,CD ⊥AC∴∠1=∠2=90°答:△ABC ≌ △CDA活动和探索 如图,∠ACB=∠BDA=90°。要说明△ACB≌△BDA,需要再补充几个条件,
应补充什么条件?把它们分别写出来,
有几种不同的方法就写几种。 活动和探索小结:这节课你有什么收获呢?与你的同伴进行交流你觉得在平时的学习中注意归纳与总结对学好几何有帮助吗?再 见
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
