12.2.2单项式与多项式相乘课件(共24张PPT)
文档属性
| 名称 | 12.2.2单项式与多项式相乘课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 277.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 11:23:05 | ||
图片预览








文档简介
(共24张PPT)
12.2.2 单项式与
多项式相乘
八年级上
华师版
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.掌握单项式与多项式相乘的运算法则.
2.能够灵活地进行单项式与多项式相乘的运算.
学习目标
重点
难点
小鹿的妈妈买了一块宽为m米的长方形地毯,这块地毯有三种颜色,你能用几种方法来表示这块地毯的面积?
m
b
m
a
m
c
ma+mb+mc
m(a+b+c)
第1种方法:
第2种方法:
新课引入
一 单项式与多项式相乘的法则
为了扩大绿地面积,要把街心花园的一块长pm,宽bm的长方形绿地,向两边分别加宽am和cm,你能用几种方法表示扩大后的绿地面积?不同的表示方法之间有什么关系?如何从数学的角度认识不同的表示方法之间的关系?
a
b
c
p
新知学习
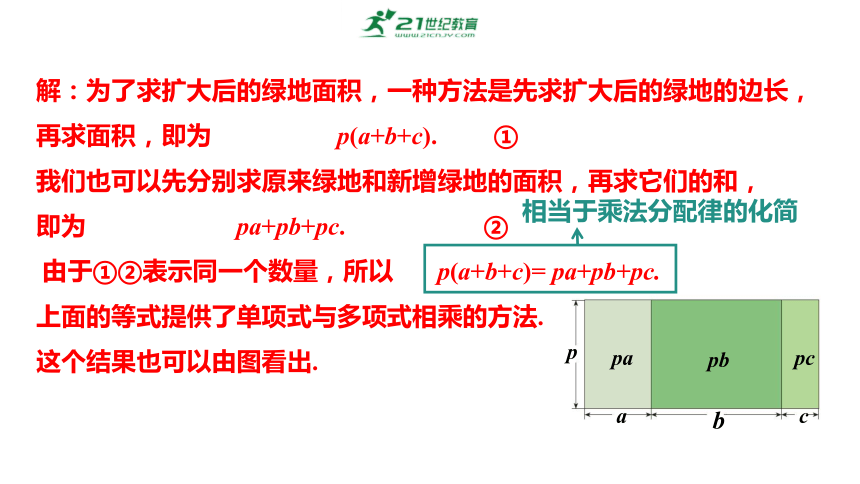
解:为了求扩大后的绿地面积,一种方法是先求扩大后的绿地的边长,再求面积,即为 p(a+b+c). ①
我们也可以先分别求原来绿地和新增绿地的面积,再求它们的和,
即为 pa+pb+pc. ②
由于①②表示同一个数量,所以 p(a+b+c)= pa+pb+pc.
上面的等式提供了单项式与多项式相乘的方法.
这个结果也可以由图看出.
a
b
c
p
pa
pb
pc
相当于乘法分配律的化简
pa+pb+pc
p(a+b+c)
p (a + b+ c)
pb
+
pc
pa
+
根据乘法的分配律
归纳
单项式乘多项式的乘法法则
单项式与多项式相乘,将单项式分别乘以多项式的每一项,再将所得的积相加.
m
b
m
a
m
c
ma+mb+mc
m(a+b+c)
第1种方法:
第2种方法:
试一试
计算:2a2·(3a2-5b).
根据乘法分配律,乘以它的每一项.
解:原式=2a2·3a2 +2a2·(-5b)
=6a4 - 10a2b.
例1 计算:(-2a2)·(3ab2 - 5ab3).
解:(-2a2)·(3ab2 - 5ab3)
=(-2a2)·3ab2 + (-2a2)·(-5ab3)
=-6a3b2 + 10a3b3.
单项式与多项式相乘
单项式与单项式相乘
乘法分配律
转化
例2 先化简,再求值:x2(3 - x) + x(x2 - 2x) + 1,其中 x = -3.
方法:直接将已知数值代入式子求值运算量大,一般是先化简,再将数值代入化简后的式子求值.
解:原式 = 3x2 - x3 + x3 - 2x2 + 1 = x2+1.
当x = -3 时,
原式 = (-3)2 + 1 = 9 + 1 = 10.
你答对了吗?
温馨提示
1.注意活用乘法分配律,将积的问题转化为和的问题,不要漏项;
2.注意确定积的每一项的符号时,既要看单项式的符号,又要看多项式每一项的符号;
3.注意单项式与多项式相乘,其积仍是多项式且积的项数与多项式的项数相同.
例3.计算:
(1)(-4x)·(2x2+3x-1);
解:(1)原式=(-4x)·(2x2)+(-4x)·3x+(-4x)·(-1)
=-8x3-12x2+4x;
(2)原式=
(2)
(3)-2x2·(xy+y2)-5x(x2y-xy2).
解:原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2)
= -2x3 y+(-2x2y2)+(-5x3y)+5x2y2
= -7x3 y+3x2y2.
1.先化简,再求值:-a(a2 - 2ab - b2) - b(ab + 2a2 - 4b2),其中 a = 2,b= .
解:-a(a2 - 2ab - b2) - b(ab + 2a2 - 4b2)
= -a3 + 2a2b + ab2 - ab2 - 2a2b + 4b3
= -a3 + 4b3.
当 a = 2,b = 时,
原式 = -23+4× = -8 =
针对训练
二 单项式与多项式相乘的法则的应用
A
B
C
3a+2b
2a-b
4a
例4 如图,一块长方形基地用来种植A、B、C 3种不同的蔬菜,求这块地的面积.
解:由题意得,
4a[(3a + 2b) + (2a - b)]
= 4a(5a + b)
= 4a·5a + 4a·b
= 20a2 + 4ab.
答:这块地的面积为20a2 + 4ab.
针对训练
1.要使x(x + a) + 3x - 2b = x2 + 5x + 4成立,则a、b的值分别为( )
A. a = -2,b = -2
B. a = 2,b = 2
C. a = 2,b = -2
D. a = -2,b = 2
C
化简后各项应该对应相等
2.今天数学课上,老师讲了单项式乘多项式,放学回到家,小明拿出课堂笔记复习,发现一道题:-3xy(4y-2x-1) = -12xy2+6x2y+□,□的地方被钢笔水弄污了,你认为□内应填写 ( )
A. 3x
B. -3xy
C. -1
D. 1
A
A
3. 如果一个三角形的底边长为 2x2y + xy - y2,高为 6xy,则这个三角形的面积是 ( )
A. 6x3y2 + 3x2y2 - 3xy3
B. 6x3y2 + 3xy - 3xy3
C. 6x3y2 + 3x2y2 - y2
D. 6x3y + 3x2y2
随堂练习
1.已知2y = x2 - 3,求2x(x - 3y) - 2y(2 - 3x) - 4 的值.
解:∵ 2x(x - 3y) - 2y(2 - 3x) - 4
=2x2-6xy + 6xy - 4y - 4
=2x2 - 4y - 4
∵2y = x2 - 3,
∴x2 - 2y = 3,
∴原式=2(2x2 - 4y) - 4 = 2× 3 - 4 = 2
2.已知(-2x)2·(3x2 - mx - 6) - 3x3 + x2中不含 x 的三次项,试确定 m 的值.
解:原式 = 4x2·(3x2 - mx - 6) - 3x3 + x2
=12x4-4mx3-24x2 - 3x3 + x2
=12x4 - (4m + 3)x3 - 23x2.
∵原式不含x3项,所以4m + 3 = 0.
∴m =
3. (1)若 a2 + a - 1 = 0,求 a3 + 2a2 + 2022 的值;
解:由 a2 + a - 1 = 0,得a2 + a = 1.
a3 + 2a2 + 2020 = a(a2 + a) + a2 + 2022 = a2 + a + 2022 = 2023.
(2) 如果 x + x2 + x3 + x4 = 0,求x + x2 + x3 + … + x2023 + x2024 的值.
解:x + x2 + x3 + … + x2019 + x2020
= (x + x2 + x3 + x4) + (x5 + x6 + x7 + x8) + … + (x2021 + x2022 + x2023 + x2024)
= (x + x2 + x3 + x4) + x4(x + x2 + x3 + x4) + x8(x+x2+x3+x4)+…+x2020(x+x2+x3+x4)
= 0.
(2) 如果 x + x2 + x3 + x4 = 0,求x + x2 + x3 + … + x2023 + x2024 的值.
解:x + x2 + x3 + … + x2019 + x2020
= (x + x2 + x3 + x4) + (x5 + x6 + x7 + x8) + … + (x2021 + x2022 + x2023 + x2024)
= (x + x2 + x3 + x4) + x4(x + x2 + x3 + x4) + x8(x+x2+x3+x4)+…+x2020(x+x2+x3+x4)
= 0.
注意
法则
单项式与
多项式相乘
(1)计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时,同号相乘得正,异号相乘得负
(2)不要出现漏乘现象
(3)运算要有顺序:先乘方,再乘除,最后加减
(4)对于混合运算,注意最后应合并同类项
单项式与多项式相乘,将单项式分别乘以多项式的每一项,再将所得的积相加.
课堂小结
12.2.2 单项式与
多项式相乘
八年级上
华师版
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.掌握单项式与多项式相乘的运算法则.
2.能够灵活地进行单项式与多项式相乘的运算.
学习目标
重点
难点
小鹿的妈妈买了一块宽为m米的长方形地毯,这块地毯有三种颜色,你能用几种方法来表示这块地毯的面积?
m
b
m
a
m
c
ma+mb+mc
m(a+b+c)
第1种方法:
第2种方法:
新课引入
一 单项式与多项式相乘的法则
为了扩大绿地面积,要把街心花园的一块长pm,宽bm的长方形绿地,向两边分别加宽am和cm,你能用几种方法表示扩大后的绿地面积?不同的表示方法之间有什么关系?如何从数学的角度认识不同的表示方法之间的关系?
a
b
c
p
新知学习
解:为了求扩大后的绿地面积,一种方法是先求扩大后的绿地的边长,再求面积,即为 p(a+b+c). ①
我们也可以先分别求原来绿地和新增绿地的面积,再求它们的和,
即为 pa+pb+pc. ②
由于①②表示同一个数量,所以 p(a+b+c)= pa+pb+pc.
上面的等式提供了单项式与多项式相乘的方法.
这个结果也可以由图看出.
a
b
c
p
pa
pb
pc
相当于乘法分配律的化简
pa+pb+pc
p(a+b+c)
p (a + b+ c)
pb
+
pc
pa
+
根据乘法的分配律
归纳
单项式乘多项式的乘法法则
单项式与多项式相乘,将单项式分别乘以多项式的每一项,再将所得的积相加.
m
b
m
a
m
c
ma+mb+mc
m(a+b+c)
第1种方法:
第2种方法:
试一试
计算:2a2·(3a2-5b).
根据乘法分配律,乘以它的每一项.
解:原式=2a2·3a2 +2a2·(-5b)
=6a4 - 10a2b.
例1 计算:(-2a2)·(3ab2 - 5ab3).
解:(-2a2)·(3ab2 - 5ab3)
=(-2a2)·3ab2 + (-2a2)·(-5ab3)
=-6a3b2 + 10a3b3.
单项式与多项式相乘
单项式与单项式相乘
乘法分配律
转化
例2 先化简,再求值:x2(3 - x) + x(x2 - 2x) + 1,其中 x = -3.
方法:直接将已知数值代入式子求值运算量大,一般是先化简,再将数值代入化简后的式子求值.
解:原式 = 3x2 - x3 + x3 - 2x2 + 1 = x2+1.
当x = -3 时,
原式 = (-3)2 + 1 = 9 + 1 = 10.
你答对了吗?
温馨提示
1.注意活用乘法分配律,将积的问题转化为和的问题,不要漏项;
2.注意确定积的每一项的符号时,既要看单项式的符号,又要看多项式每一项的符号;
3.注意单项式与多项式相乘,其积仍是多项式且积的项数与多项式的项数相同.
例3.计算:
(1)(-4x)·(2x2+3x-1);
解:(1)原式=(-4x)·(2x2)+(-4x)·3x+(-4x)·(-1)
=-8x3-12x2+4x;
(2)原式=
(2)
(3)-2x2·(xy+y2)-5x(x2y-xy2).
解:原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2)
= -2x3 y+(-2x2y2)+(-5x3y)+5x2y2
= -7x3 y+3x2y2.
1.先化简,再求值:-a(a2 - 2ab - b2) - b(ab + 2a2 - 4b2),其中 a = 2,b= .
解:-a(a2 - 2ab - b2) - b(ab + 2a2 - 4b2)
= -a3 + 2a2b + ab2 - ab2 - 2a2b + 4b3
= -a3 + 4b3.
当 a = 2,b = 时,
原式 = -23+4× = -8 =
针对训练
二 单项式与多项式相乘的法则的应用
A
B
C
3a+2b
2a-b
4a
例4 如图,一块长方形基地用来种植A、B、C 3种不同的蔬菜,求这块地的面积.
解:由题意得,
4a[(3a + 2b) + (2a - b)]
= 4a(5a + b)
= 4a·5a + 4a·b
= 20a2 + 4ab.
答:这块地的面积为20a2 + 4ab.
针对训练
1.要使x(x + a) + 3x - 2b = x2 + 5x + 4成立,则a、b的值分别为( )
A. a = -2,b = -2
B. a = 2,b = 2
C. a = 2,b = -2
D. a = -2,b = 2
C
化简后各项应该对应相等
2.今天数学课上,老师讲了单项式乘多项式,放学回到家,小明拿出课堂笔记复习,发现一道题:-3xy(4y-2x-1) = -12xy2+6x2y+□,□的地方被钢笔水弄污了,你认为□内应填写 ( )
A. 3x
B. -3xy
C. -1
D. 1
A
A
3. 如果一个三角形的底边长为 2x2y + xy - y2,高为 6xy,则这个三角形的面积是 ( )
A. 6x3y2 + 3x2y2 - 3xy3
B. 6x3y2 + 3xy - 3xy3
C. 6x3y2 + 3x2y2 - y2
D. 6x3y + 3x2y2
随堂练习
1.已知2y = x2 - 3,求2x(x - 3y) - 2y(2 - 3x) - 4 的值.
解:∵ 2x(x - 3y) - 2y(2 - 3x) - 4
=2x2-6xy + 6xy - 4y - 4
=2x2 - 4y - 4
∵2y = x2 - 3,
∴x2 - 2y = 3,
∴原式=2(2x2 - 4y) - 4 = 2× 3 - 4 = 2
2.已知(-2x)2·(3x2 - mx - 6) - 3x3 + x2中不含 x 的三次项,试确定 m 的值.
解:原式 = 4x2·(3x2 - mx - 6) - 3x3 + x2
=12x4-4mx3-24x2 - 3x3 + x2
=12x4 - (4m + 3)x3 - 23x2.
∵原式不含x3项,所以4m + 3 = 0.
∴m =
3. (1)若 a2 + a - 1 = 0,求 a3 + 2a2 + 2022 的值;
解:由 a2 + a - 1 = 0,得a2 + a = 1.
a3 + 2a2 + 2020 = a(a2 + a) + a2 + 2022 = a2 + a + 2022 = 2023.
(2) 如果 x + x2 + x3 + x4 = 0,求x + x2 + x3 + … + x2023 + x2024 的值.
解:x + x2 + x3 + … + x2019 + x2020
= (x + x2 + x3 + x4) + (x5 + x6 + x7 + x8) + … + (x2021 + x2022 + x2023 + x2024)
= (x + x2 + x3 + x4) + x4(x + x2 + x3 + x4) + x8(x+x2+x3+x4)+…+x2020(x+x2+x3+x4)
= 0.
(2) 如果 x + x2 + x3 + x4 = 0,求x + x2 + x3 + … + x2023 + x2024 的值.
解:x + x2 + x3 + … + x2019 + x2020
= (x + x2 + x3 + x4) + (x5 + x6 + x7 + x8) + … + (x2021 + x2022 + x2023 + x2024)
= (x + x2 + x3 + x4) + x4(x + x2 + x3 + x4) + x8(x+x2+x3+x4)+…+x2020(x+x2+x3+x4)
= 0.
注意
法则
单项式与
多项式相乘
(1)计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时,同号相乘得正,异号相乘得负
(2)不要出现漏乘现象
(3)运算要有顺序:先乘方,再乘除,最后加减
(4)对于混合运算,注意最后应合并同类项
单项式与多项式相乘,将单项式分别乘以多项式的每一项,再将所得的积相加.
课堂小结
