2024-2025学年河南省南阳市南召县九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年河南省南阳市南召县九年级(上)开学数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 122.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 00:00:00 | ||
图片预览

文档简介
2024-2025学年河南省南阳市南召县九年级(上)开学数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若分式有意义,则满足的条件是( )
A. B. C. D.
2.宋朝杨万里有诗曰:“只道花无十日红,此花无日不春风一尖已剥胭脂笔,四破犹包翡翠茸”月季被誉为“花中皇后”,月季也是南阳市的市花,具有非常高的观赏价值某品种的月季花粉直径约为米,则数据用科学记数法表示为( )
A. B. C. D.
3.如图,枫叶遮盖了一点,则点的坐标可能是( )
A. B.
C. D.
4.某中学规定:学生的学期体育综合成绩满分为分,其中,期中考试成绩占,期末考试成绩占,小海同学这个学期的期中、期末成绩百分制分别是分、分,则小海这个学期的体育综合成绩是( )
A. 分 B. 分 C. 分 D. 分
5.小明是这样画平行四边形的:如图,将三角尺的一边贴着直尺推移到的位置,这时四边形就是平行四边形小明这样做的依据是( )
A. 有两组对边分别平行的四边形是平行四边形
B. 有两组对边分别相等的四边形是平行四边形
C. 有一组对边平行且相等的四边形是平行四边形
D. 对角线互相平分的四边形是平行四边形
6.已知点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B. C. D.
7.如图,菱形的对角线,交于点,,,将绕点顺时针方向旋转得到,连接若点的对应点恰好落在线段上,则的面积是( )
A.
B.
C.
D.
8.已知关于的分式方程的解是非负数,则的取值范圈是( )
A. B. C. 或 D. 或
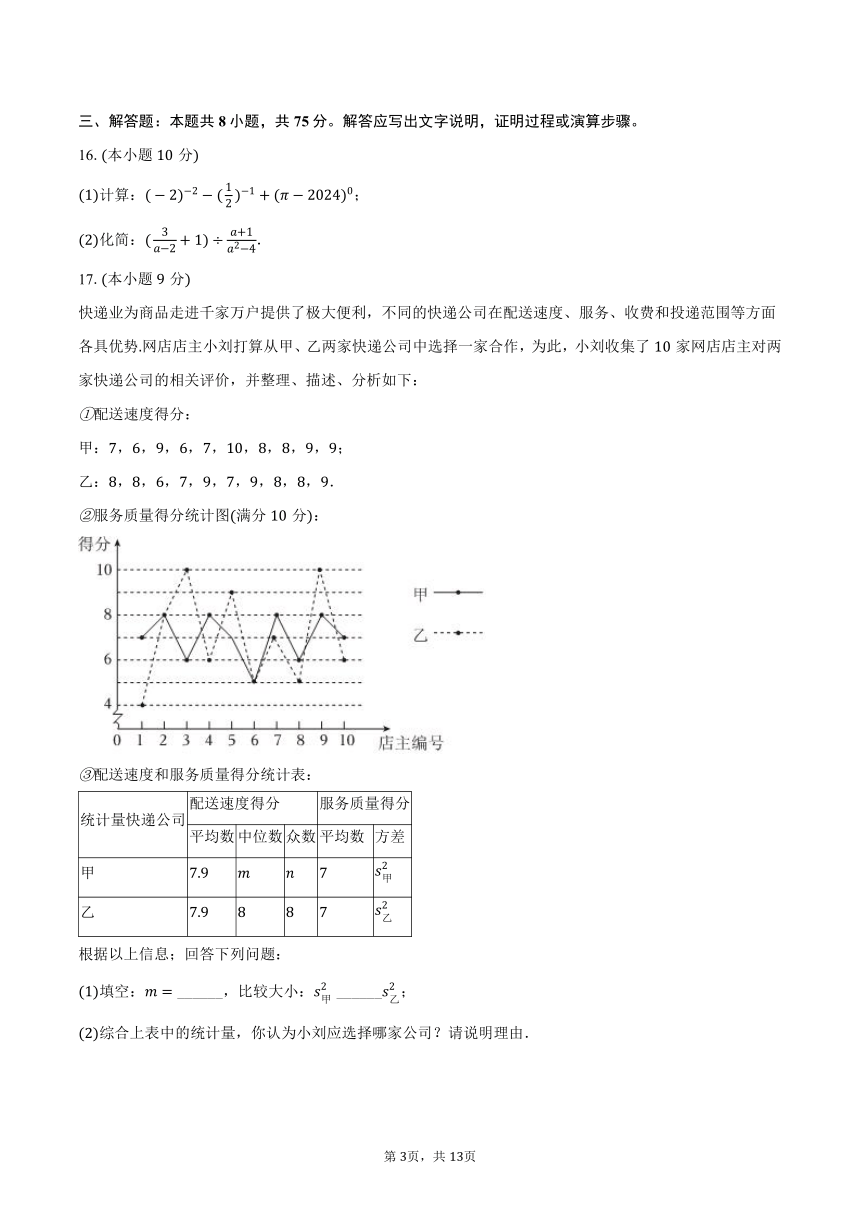
9.如图,射线、分别表示买牛肉和买猪肉所需费用单位:元与购买数量单位:千克的关系,已知买牛肉每千克所需的费用比买猪肉每千克所需的费用的倍少元,设买猪肉每千克所需的费用为元,则可列方程为( )
A. B. C. D.
10.如图,是正方形对角线上一点,,,,分别为垂足若,,则的长为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.写出一个分式,并保证无论字母取何值分式均有意义______.
12.名学生的鞋号由小到大是:,,,,,,,,,这组数据的平均数、中位数和众数中,指标______是鞋厂最感兴趣的填“平均数”或“中位数”或“众数”.
13.直线向下平移个单位所得到的直线不经过的象限是______.
14.如图,在平行四边形中,的平分线交于点,的平分线交于点,若,,则的长为______.
15.如图,反比例函数的图象经过 对角线的交点,已知点、、在坐标轴上,, 的面积为,则 ______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:;
化简:.
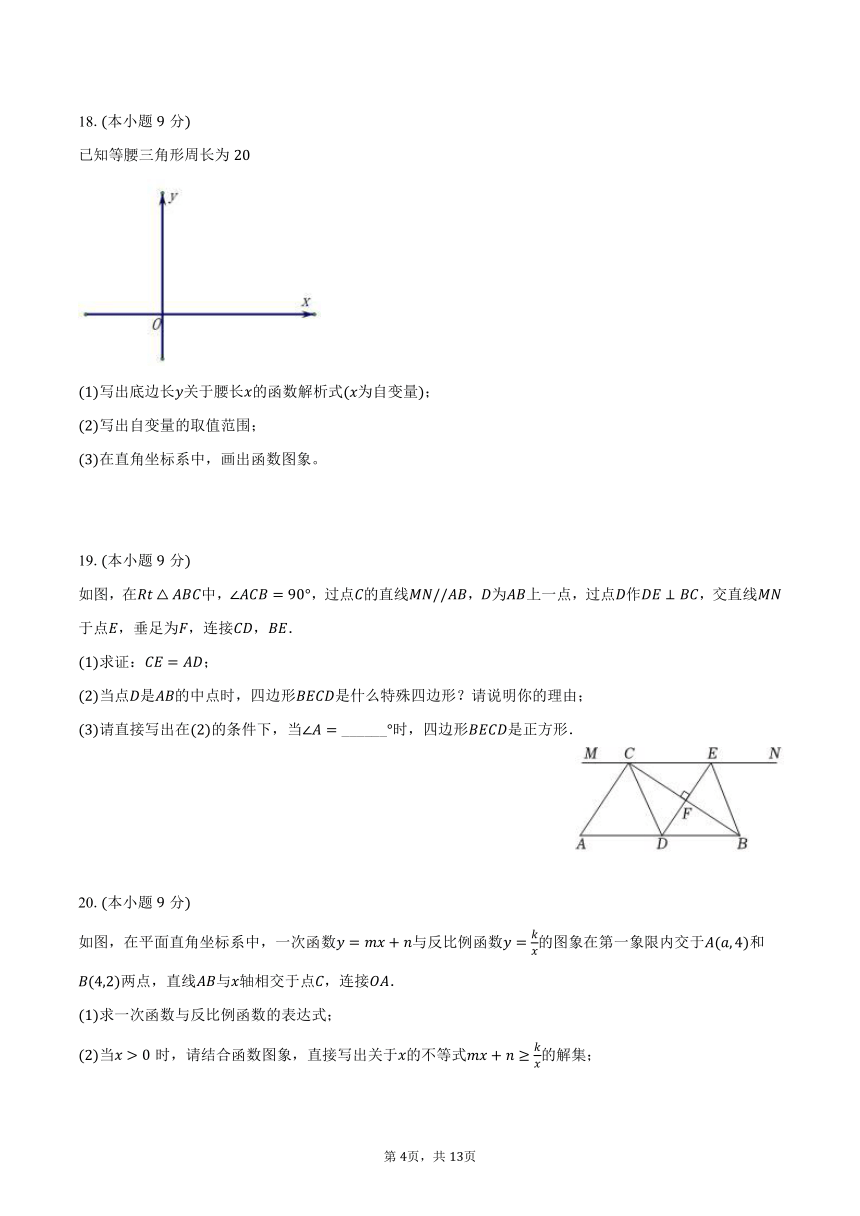
17.本小题分
快递业为商品走进千家万户提供了极大便利,不同的快递公司在配送速度、服务、收费和投递范围等方面各具优势网店店主小刘打算从甲、乙两家快递公司中选择一家合作,为此,小刘收集了家网店店主对两家快递公司的相关评价,并整理、描述、分析如下:
配送速度得分:
甲:,,,,,,,,,;
乙:,,,,,,,,,.
服务质量得分统计图满分分:
配送速度和服务质量得分统计表:
统计量快递公司 配送速度得分 服务质量得分
平均数 中位数 众数 平均数 方差
甲
乙
根据以上信息;回答下列问题:
填空: ______,比较大小: ______;
综合上表中的统计量,你认为小刘应选择哪家公司?请说明理由.
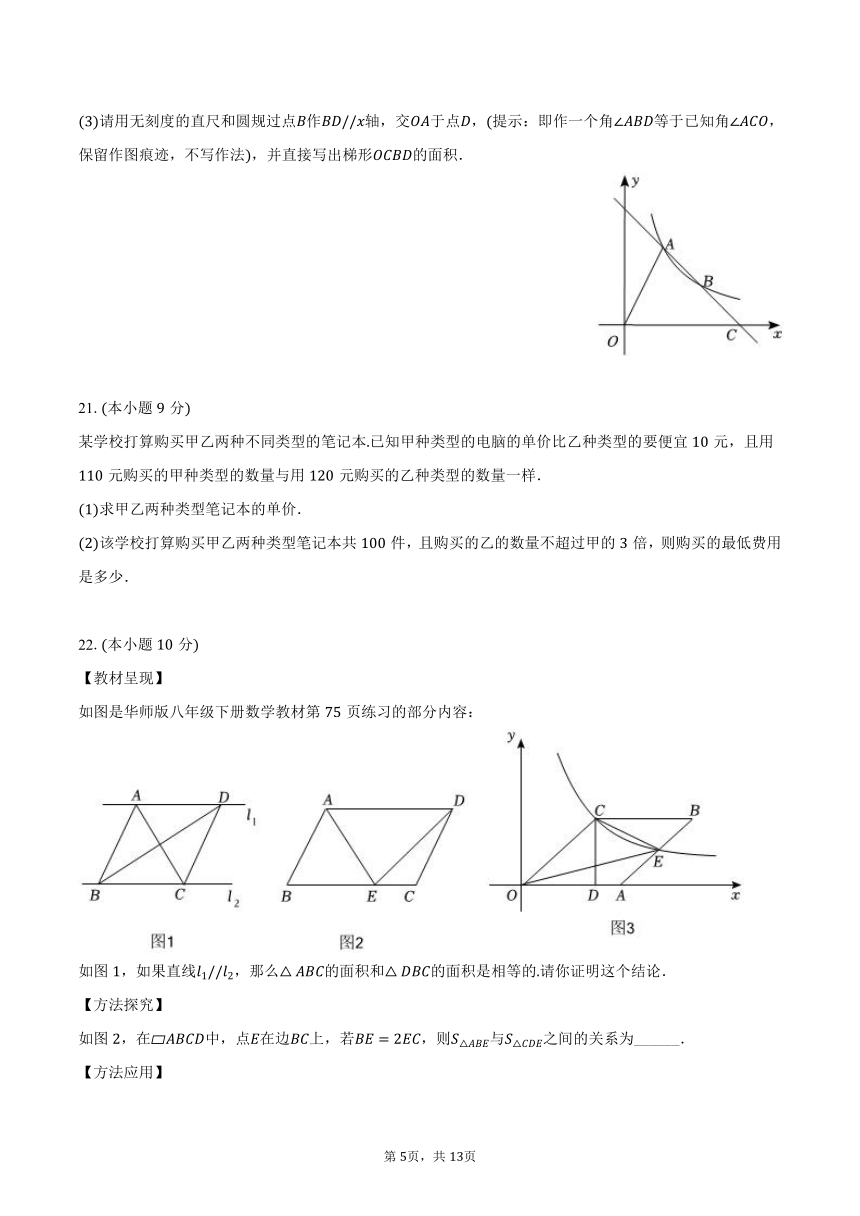
18.本小题分
已知等腰三角形周长为
写出底边长关于腰长的函数解析式为自变量;
写出自变量的取值范围;
在直角坐标系中,画出函数图象。
19.本小题分
如图,在中,,过点的直线,为上一点,过点作,交直线于点,垂足为,连接,.
求证:;
当点是的中点时,四边形是什么特殊四边形?请说明你的理由;
请直接写出在的条件下,当 ______时,四边形是正方形.
20.本小题分
如图,在平面直角坐标系中,一次函数与反比例函数的图象在第一象限内交于和两点,直线与轴相交于点,连接.
求一次函数与反比例函数的表达式;
当时,请结合函数图象,直接写出关于的不等式的解集;
请用无刻度的直尺和圆规过点作轴,交于点,提示:即作一个角等于已知角,保留作图痕迹,不写作法,并直接写出梯形的面积.
21.本小题分
某学校打算购买甲乙两种不同类型的笔记本已知甲种类型的电脑的单价比乙种类型的要便宜元,且用元购买的甲种类型的数量与用元购买的乙种类型的数量一样.
求甲乙两种类型笔记本的单价.
该学校打算购买甲乙两种类型笔记本共件,且购买的乙的数量不超过甲的倍,则购买的最低费用是多少.
22.本小题分
【教材呈现】
如图是华师版八年级下册数学教材第页练习的部分内容:
如图,如果直线,那么的面积和的面积是相等的请你证明这个结论.
【方法探究】
如图,在 中,点在边上,若,则与之间的关系为______.
【方法应用】
如图,已知四边形是菱形,轴,垂足为,函数的图象经过点,且与交于点若,求的面积.
23.本小题分
特例感知如图,在正方形中,点,分别为,的中点,、交于点.
证明:.
初步探究如图,在正方形中,点为边上一点,分别交、于、,垂足为求证:.
基本应用如图,将边长为的正方形折叠,使得点落在边的中点处,折痕为,点、分别在边、边上,求出折痕的长.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.答案不唯一
12.众数
13.二
14.
15.
16.解:原式
;
原式
.
17.,.
小刘应选择甲公司,理由如下:
配送速度方面,甲乙两公司的平均分相同,中位数相同,但甲的众数高于乙公司,这说明甲在配送速度方面可能比乙公司表现的更好,
服务质量方面,二者的平均相同,但甲的方差明显小于乙,说甲的服务质量更稳定,因此应该选择甲公司.
18.解:写出底边长关于腰长的函数解析式是 ;
由两腰的和小于周长,两边之和大于第三边得
解得,
自变量的取值范围是;
如图:
.
19.证明:,
,
,
,
,
,即,
四边形是平行四边形,
;
解:四边形是菱形,
理由是:为中点,
,
,
,
,
四边形是平行四边形,
,为中点,
,
四边形是菱形;
.
20.解:反比例函数图象点,
,
反比例函数的表达式为:,
把代入得:,
,
一次函数的图象过点,点,
,
解得:,
一次函数的表达式为 ;
观察函数图象可得, 的解集为: ;
用作一个角等于已知角的方法作出,如下图:
由一次函数的表达式知,点,
由点的坐标得,直线的表达式为:,
当时,,
则,
即点,则,
则梯形的面积.
21.解:设甲类型的笔记本单价为元,则乙类型的笔记本单价为元,
由题意得,,
解得,
经检验是原方程的解,且符合题意,
乙类型的笔记本单价为元,
答:甲类型的笔记本单价为元,乙类型的笔记本单价为元;
设甲类型笔记本购买了件,费用为元,则乙类型的笔记本购买了件,
购买的乙的数量不超过甲的倍,
,且,
解得,
根据题意得,
,
随的增大而减小,
时,最小值为元,
答:最低费用为元.
22.
【解析】【教材呈现】
证明:过点作于点,过点作于点,如图所示,
,
,
四边形为平行四边形,
,
,,
;
【方法探究】解:由教材呈现可知:
,
与两底,上的高相等,
:::,
;
故答案为:;
【方法应用】
解:连接,
,轴,
点的横坐标为,
当时,,则,
由勾股定理得:,
由菱形的性质,可知,
,
与同底等高,
.
23.证明:四边形是正方形,
,,
又点,分别为,的中点,
,
,
在与中,
,
≌,
,
,
,
,
即;
证明:过点作交于点,交于点.
,,
四边形是平行四边形,
,
,,
,
,
,
,,
≌,
;
解:连接,由折叠可知,
由可知,
点是的中点,
,
在中,由勾股定理得:,
的长为.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若分式有意义,则满足的条件是( )
A. B. C. D.
2.宋朝杨万里有诗曰:“只道花无十日红,此花无日不春风一尖已剥胭脂笔,四破犹包翡翠茸”月季被誉为“花中皇后”,月季也是南阳市的市花,具有非常高的观赏价值某品种的月季花粉直径约为米,则数据用科学记数法表示为( )
A. B. C. D.
3.如图,枫叶遮盖了一点,则点的坐标可能是( )
A. B.
C. D.
4.某中学规定:学生的学期体育综合成绩满分为分,其中,期中考试成绩占,期末考试成绩占,小海同学这个学期的期中、期末成绩百分制分别是分、分,则小海这个学期的体育综合成绩是( )
A. 分 B. 分 C. 分 D. 分
5.小明是这样画平行四边形的:如图,将三角尺的一边贴着直尺推移到的位置,这时四边形就是平行四边形小明这样做的依据是( )
A. 有两组对边分别平行的四边形是平行四边形
B. 有两组对边分别相等的四边形是平行四边形
C. 有一组对边平行且相等的四边形是平行四边形
D. 对角线互相平分的四边形是平行四边形
6.已知点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B. C. D.
7.如图,菱形的对角线,交于点,,,将绕点顺时针方向旋转得到,连接若点的对应点恰好落在线段上,则的面积是( )
A.
B.
C.
D.
8.已知关于的分式方程的解是非负数,则的取值范圈是( )
A. B. C. 或 D. 或
9.如图,射线、分别表示买牛肉和买猪肉所需费用单位:元与购买数量单位:千克的关系,已知买牛肉每千克所需的费用比买猪肉每千克所需的费用的倍少元,设买猪肉每千克所需的费用为元,则可列方程为( )
A. B. C. D.
10.如图,是正方形对角线上一点,,,,分别为垂足若,,则的长为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.写出一个分式,并保证无论字母取何值分式均有意义______.
12.名学生的鞋号由小到大是:,,,,,,,,,这组数据的平均数、中位数和众数中,指标______是鞋厂最感兴趣的填“平均数”或“中位数”或“众数”.
13.直线向下平移个单位所得到的直线不经过的象限是______.
14.如图,在平行四边形中,的平分线交于点,的平分线交于点,若,,则的长为______.
15.如图,反比例函数的图象经过 对角线的交点,已知点、、在坐标轴上,, 的面积为,则 ______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:;
化简:.
17.本小题分
快递业为商品走进千家万户提供了极大便利,不同的快递公司在配送速度、服务、收费和投递范围等方面各具优势网店店主小刘打算从甲、乙两家快递公司中选择一家合作,为此,小刘收集了家网店店主对两家快递公司的相关评价,并整理、描述、分析如下:
配送速度得分:
甲:,,,,,,,,,;
乙:,,,,,,,,,.
服务质量得分统计图满分分:
配送速度和服务质量得分统计表:
统计量快递公司 配送速度得分 服务质量得分
平均数 中位数 众数 平均数 方差
甲
乙
根据以上信息;回答下列问题:
填空: ______,比较大小: ______;
综合上表中的统计量,你认为小刘应选择哪家公司?请说明理由.
18.本小题分
已知等腰三角形周长为
写出底边长关于腰长的函数解析式为自变量;
写出自变量的取值范围;
在直角坐标系中,画出函数图象。
19.本小题分
如图,在中,,过点的直线,为上一点,过点作,交直线于点,垂足为,连接,.
求证:;
当点是的中点时,四边形是什么特殊四边形?请说明你的理由;
请直接写出在的条件下,当 ______时,四边形是正方形.
20.本小题分
如图,在平面直角坐标系中,一次函数与反比例函数的图象在第一象限内交于和两点,直线与轴相交于点,连接.
求一次函数与反比例函数的表达式;
当时,请结合函数图象,直接写出关于的不等式的解集;
请用无刻度的直尺和圆规过点作轴,交于点,提示:即作一个角等于已知角,保留作图痕迹,不写作法,并直接写出梯形的面积.
21.本小题分
某学校打算购买甲乙两种不同类型的笔记本已知甲种类型的电脑的单价比乙种类型的要便宜元,且用元购买的甲种类型的数量与用元购买的乙种类型的数量一样.
求甲乙两种类型笔记本的单价.
该学校打算购买甲乙两种类型笔记本共件,且购买的乙的数量不超过甲的倍,则购买的最低费用是多少.
22.本小题分
【教材呈现】
如图是华师版八年级下册数学教材第页练习的部分内容:
如图,如果直线,那么的面积和的面积是相等的请你证明这个结论.
【方法探究】
如图,在 中,点在边上,若,则与之间的关系为______.
【方法应用】
如图,已知四边形是菱形,轴,垂足为,函数的图象经过点,且与交于点若,求的面积.
23.本小题分
特例感知如图,在正方形中,点,分别为,的中点,、交于点.
证明:.
初步探究如图,在正方形中,点为边上一点,分别交、于、,垂足为求证:.
基本应用如图,将边长为的正方形折叠,使得点落在边的中点处,折痕为,点、分别在边、边上,求出折痕的长.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.答案不唯一
12.众数
13.二
14.
15.
16.解:原式
;
原式
.
17.,.
小刘应选择甲公司,理由如下:
配送速度方面,甲乙两公司的平均分相同,中位数相同,但甲的众数高于乙公司,这说明甲在配送速度方面可能比乙公司表现的更好,
服务质量方面,二者的平均相同,但甲的方差明显小于乙,说甲的服务质量更稳定,因此应该选择甲公司.
18.解:写出底边长关于腰长的函数解析式是 ;
由两腰的和小于周长,两边之和大于第三边得
解得,
自变量的取值范围是;
如图:
.
19.证明:,
,
,
,
,
,即,
四边形是平行四边形,
;
解:四边形是菱形,
理由是:为中点,
,
,
,
,
四边形是平行四边形,
,为中点,
,
四边形是菱形;
.
20.解:反比例函数图象点,
,
反比例函数的表达式为:,
把代入得:,
,
一次函数的图象过点,点,
,
解得:,
一次函数的表达式为 ;
观察函数图象可得, 的解集为: ;
用作一个角等于已知角的方法作出,如下图:
由一次函数的表达式知,点,
由点的坐标得,直线的表达式为:,
当时,,
则,
即点,则,
则梯形的面积.
21.解:设甲类型的笔记本单价为元,则乙类型的笔记本单价为元,
由题意得,,
解得,
经检验是原方程的解,且符合题意,
乙类型的笔记本单价为元,
答:甲类型的笔记本单价为元,乙类型的笔记本单价为元;
设甲类型笔记本购买了件,费用为元,则乙类型的笔记本购买了件,
购买的乙的数量不超过甲的倍,
,且,
解得,
根据题意得,
,
随的增大而减小,
时,最小值为元,
答:最低费用为元.
22.
【解析】【教材呈现】
证明:过点作于点,过点作于点,如图所示,
,
,
四边形为平行四边形,
,
,,
;
【方法探究】解:由教材呈现可知:
,
与两底,上的高相等,
:::,
;
故答案为:;
【方法应用】
解:连接,
,轴,
点的横坐标为,
当时,,则,
由勾股定理得:,
由菱形的性质,可知,
,
与同底等高,
.
23.证明:四边形是正方形,
,,
又点,分别为,的中点,
,
,
在与中,
,
≌,
,
,
,
,
即;
证明:过点作交于点,交于点.
,,
四边形是平行四边形,
,
,,
,
,
,
,,
≌,
;
解:连接,由折叠可知,
由可知,
点是的中点,
,
在中,由勾股定理得:,
的长为.
第1页,共1页
同课章节目录
