第三单元:小数除法(单元复习课件)-人教版五年级数学上册(共38张PPT)
文档属性
| 名称 | 第三单元:小数除法(单元复习课件)-人教版五年级数学上册(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 00:00:00 | ||
图片预览











文档简介
(共38张PPT)
人教版五年级数学上册
第三单元:小数除法单元复习专题
掌握小数除法的计算方法,并能正确地进行计算;能根据算式的特点合理选择计算方法,体会转化的数学思想。
掌握用“四舍五入”法取商的近似数,能根据实际情况合理运用“进一法”和“去尾法”取商的近似数。
认识循环小数、有限小数和无限小数;能借助计算器探索规律,并应用规律解决问题,提高学生自主探究问题的能力。
掌握小数除法的计算方法;能正确地进行小数除法的笔算和简便计算;能正确应用“四舍五入”法取商的近似数。
掌握确定小数除法中商的小数点位置的方法;会把除数是小数的除法转化成除数是整数的除法,并能正确地进行计算。
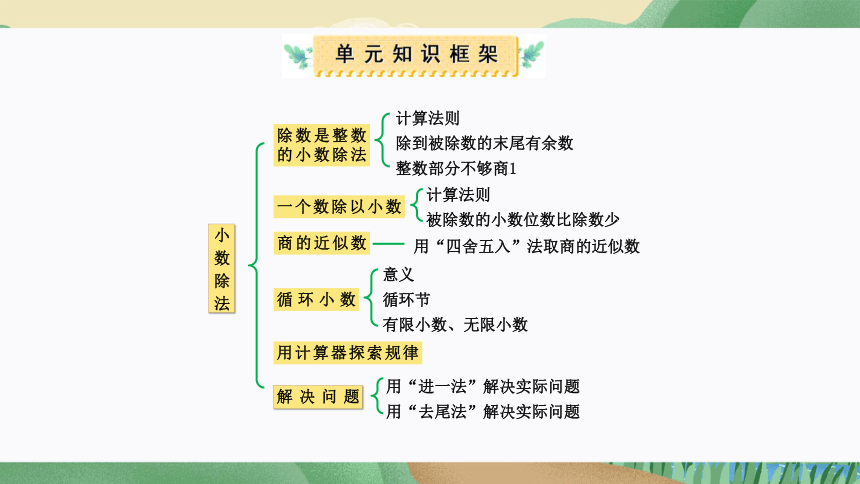
小数除法
除数是整数的小数除法
计算法则
除到被除数的末尾有余数
整数部分不够商1
一个数除以小数
计算法则
被除数的小数位数比除数少
商的近似数
用“四舍五入”法取商的近似数
循环小数
意义
循环节
有限小数、无限小数
解决问题
用“进一法”解决实际问题
用“去尾法”解决实际问题
用计算器探索规律
知识点01:除数是整数的小数除法
1、除数是整数的小数除法计算法则:
(1)小数除以整数,按照整数除法的方法去除;
(2)商的小数点要和被除数的小数点对齐;
(3)除得的商的哪一位不够商1,就在那一位上写0,再继续除;
(4)如果除到被除数的末尾仍有余数,就在余数的后面添0再除。
【例1】列竖式计算。
(1)25.8÷3= (2)2.03÷7=
25.8
3
.
8
24
6
8
18
0
1
8.6
0.29
2.03
7
.
0
14
9
3
63
0
6
2
商的哪一位不够商1,就在那一位上写0。
【例1】列竖式计算。
(3)30.5÷5= (4)6.57÷9=
30.5
5
.
6
30
1
5
5
0
6.1
0.73
6.57
9
.
0
63
3
7
27
0
2
7
【例2】31.2是( ) 的6倍。
A、5.2 B、6.7 C、187.2
求31.2是多少的6倍,根据已知一个数的几倍是多少,求这个数,用除法计算。
31.2÷6=5.2
A
【例3】“妈妈买了4千克水果,共用去了26.8元,每千克水果多少元?”图中竖式中箭头所指“28”表示( )。
A、28元 B、28千克
C、2.8元 D、2.8千克
箭头所指的“28”中的“8”对应的是十分位,代表28个0.1元。28×0.1=2.8,所以竖式中箭头所指“28”表示2.8元。
C
【例4】一艘货轮从港口出发,3小时航行160.8千米,平均每小时航行多少千米?
【解析】根据速度=路程÷时间,代入数值计算即可。
【解答】
160.8÷3=53.6(千米)
答:平均每小时航行53.6千米。
【例5】李阿姨去超市买了2盒巧克力和3袋面包。一共花了63.8元,一袋面包8.8元。一盒巧克力多少元?
【解析】先根据总价=单价×数量,用一袋面包的价钱乘以袋数,算出3袋面包的价钱;然后用总价钱减去面包的价钱得到巧克力的总价钱;再根据单价=总价÷数量,用巧克力的总价钱除以盒数,得到一盒巧克力的价钱。
【例5】李阿姨去超市买了2盒巧克力和3袋面包。一共花了63.8元,一袋面包8.8元。一盒巧克力多少元?
【解答】
(63.8-8.8×3)÷2
=(63.8-26.4)÷2
=37.4÷2
=18.7(元)
答:一盒巧克力18.7元。
知识点02:一个数除以小数
1、一个数除以小数计算法则:
(1)先明确除数有几位小数,再移动除数的小数点,使它变成整数;
(2)除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数的末尾用“0”补足);
(3)然后按照除数是整数的小数除法进行计算。
2、小数除法的验算方法:计算小数除法也可以用乘法来验算。
【例6】列竖式计算:
(1)83.2÷2.6= (2)0.936÷0.18=
83.2
2.6
3
2
5
2
52
0
78
32
0.936
0.18
5
.
2
3
6
36
90
0
.
5.2
【例6】列竖式计算:
(3)51.7÷2.5= (4)38.7÷3.6=
20.68
51.7
2.5
2
.
0
1
6
7
50
0
150
20
0
8
200
0
位数不够的,在被除数的末尾用“0”补足。
10.75
38.7
3.6
1
.
0
2
7
7
36
0
252
18
0
5
180
0
【例7】一台普通洗衣机一次的用水量是2.73立方米,一台节水洗衣机一次的用水量是1.3立方米。一台普通洗衣机一次的用水量是一台节水洗衣机的几倍?
【解析】根据求一个数是另一个数的几倍,用除法。用普通洗衣机的用水量除以节水洗衣机的用水量即可。
【解答】
2.73÷1.3=2.1
答:一台普通洗衣机一次的用水量是一台节水洗衣机的2.1倍。
【例8】一个服装厂做一套衣服原来需要2.6米的布料,后来改进裁剪方法,每套只需2.2米的布料。原来准备做220套衣服的布料,现在可以做多少套?
【解析】先用做一套衣服原来需要的布料长度乘衣服套数,算出原来准备的布料总量,再除以现在每套衣服所需的布料量,就可得到现在能做的套数。
【例8】一个服装厂做一套衣服原来需要2.6米的布料,后来改进裁剪方法,每套只需2.2米的布料。原来准备做220套衣服的布料,现在可以做多少套?
【解答】
2.6×220÷2.2
=572÷2.2
=260(套)
答:现在可以做260套。
【例9】5台同样的起重机同时工作3.2小时,可以吊运货物20.8吨,照这样计算,一台起重机每小时可以吊运货物多少吨?
【解析】已知5台同样的起重机同时工作3.2小时可以吊运货物16吨,先用吊运货物的吨数除以时间,算出5台起重机1小时吊运货物的吨数;再用5台起重机1小时吊运货物的吨数除以起重机台数,求出1台起重机每小时吊运货物的吨数。
【例9】5台同样的起重机同时工作3.2小时,可以吊运货物20.8吨,照这样计算,一台起重机每小时可以吊运货物多少吨?
【解答】
20.8÷3.2÷5
=6.5÷5
=1.3(吨)
答:一台起重机每小时可以吊运货物1吨。
知识点03:商的近似数
1、求商的近似数时,要除到比要保留的小数位数多一位,然后按照“四舍五入”法取商的近似数。
2、注意
用“四舍”法取商的近似数,商小于准确数;
用“五入”法取商的近似数,商大于准确数
【例10】17.07÷3的商保留一位小数是( )。
除数是整数的小数除法,按照整数除法进行计算,商的小数点要与被除数的小数点对齐,被除数的数用完时,在被除数的末尾添0”继续除。
要求得数保留几位小数,要除到它的下一位,再用四舍五入的方法取商的近似数。
17.07÷3=5.69≈5.7
5.7
【例11】下面算式中,计算结果不可能是10.86的是( )。
A、1.□□×6 B、3.□□×3 C、6.□□×2
根据积÷一个因数=另外一个因数,用10.28除以每个选项中已知的因数,和另外一个因数进比较即可。
A中,10.28÷6=1.81,符合题意;
B中,10.86÷3=3.62,符合题意;
C中,10.86÷2=5.43,不符合题意;
C
【例12】甲、乙、丙三人加工同样多的零件。甲3小时完成11个,乙2小时完成9个,丙4小时完成13个,平均每小时( )做得最多。
用加工零件个数除以时间,分别求出几人每小时加工的零件个数,比较即可。
11÷3≈3.7 (个)
9÷2=4.5 (个)
13÷4≈3.3 (个)
3.3<3.7<4.5
所以每小时乙做得最多。
乙
【例13】妈妈去市场买了一大袋土豆,共重4千克。已知19个土豆约重2.5千克,估一估,这袋土豆约有( )。
A、40个以上 B、不到20个 C、30个左右
土豆个数÷相应千克数=每千克土豆的个数,每千克土豆的个数×总质量=土豆总个数,据此列式。
19÷2.5×4
=7.6×4
=30.4
≈30(个)
C
知识点04:循环小数
1、循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
2、循环节:一个循环小数的小数部分,依次不断重复出现的数字,就是这个循环小数的循环节。
3、有限小数:小数部分的位数有限的小数;
无限小数:小数部分的位数无限的小数。
4、循环小数一定是无限小数。
【例14】下列除法算式中,结果是循环小数的是( )。
A、5÷2.1 B、3.8÷6 C、9÷1.6
循环小数是指一个数的小数部分从某一位起,一个或几个数字依次重复出现的无限小数。
A选项,5÷2.1=2.38095……不是循环小数;
B选项,3.8÷6=0.63333……是循环小数;
C选项,9÷1.6=5.625是有限小数。
A
【例15】下面循环小数中,最大的是( )。
A、 B、 C、
先看整数部分,整数部分大的那个数就大;整数部分相同,十分位上的数大的那个数就大;十分位上的数相同,百分位上的数大的那个数就大……以此类推。
A选项,=0.2399999……
B选项,=0.268268268……
C选项,=0.2575757……
所以> >
B
【例16】已知9÷3.3的结果是一个循环小数,这个循环小数的小数点右边第29位的数字是( )。
9÷3.3=,商的循环节是72,每2个数字一循环;29÷2=14……1,余数是1表示是一个循环里的第一个数,即7。所以这个循环小数的小数点右边第29位的数字是7。
7
知识点05:解决问题
1、进一法:在取近似数时,不管省略部分首位上的数字是儿,都要向前一位进一。
2、去尾法:在取近似数时,不管省略部分首位上的数字是儿,都要全部舍去。
3、要根据实际情况选择用“进一法”还是“去尾法”。
用去尾法得到的近似数比准确数小。
用进一法得到的近似数比准确数大。
【例17】有一批重30吨的货物,如果用一辆限载3.2吨的货车运送,运完这批货物至少需要运( )次。
用货物的总重量除以货车的限载重量,求出运送的次数。根据实际情况,对计算结果采用“进一法”,需要再加一次运输。
30÷3.2=9.375≈10
答:张叔叔运完这批货物至少需要运10次。
10
【例18】一个箱子最多能装物品8千克,要装完86千克物品,至少需要多少个这样的箱子?
【解析】先用总物品重量除以每个箱子能装的重量,计算所需箱子的数量。结果要采用“进一法”取整,那么余下的物品也需要一个箱子。
【解答】
86÷8=10.75(个)
答:至少需要11个这样的箱子。
【例19】李叔叔用3.85米铁丝做衣架,每个衣架用0.7米铁丝。最多能做多少个?
【解析】已知铁丝的总长度和做一个衣架所需铁丝的长度,要求最多能做多少个衣架,就是求总长度里有多少个单个衣架所需的长度,用除法计算。计算结果如果有小数,因为衣架个数必须是整数,所以采用去尾法保留整数。
【解答】
3.85÷0.7=5.5(个)
答:最多能做5个。
【例20】一块长方形的铁皮长4.85米,宽2.9米,如果做一个铁箱需要用铁皮3.2平方米,这块铁皮最多可以做几个铁箱?
【解析】先根据长方形面积=长×宽计算铁皮的总面积,再用总面积除以做一个铁箱所需的铁板面积,得到的商就是能做的铁箱数量,因为铁箱个数只能为整数,所以采用去尾法保留整数。
【解答】4.8×2.9=13.92(平方米)
13.92÷3.2=4.35≈4(个)
答:这块铁皮最多可以做4个铁箱。
1、一个数的3倍是4.5,这个数是( )。
A、13.5 B、5.5 C、1.5
2、15.69÷2.5的商保留倒百分位是( )。
A、6.27 B、6.28 C、6.29
C
B
3、9.6666666是一个( ) 。
A、有限小数 B、无限小数 C、循环小数
4、在一道没有余数的除法算式里,被除数、除数和商的和是20.6,被除数是除数的5倍。除数是( )。
A
2.6
5、两人去书店买笔,明明买了8支钢笔,亮亮买了同样的5支钢笔,一共花了123.5元,那么平均每支钢笔多少元?
123.5÷(8+5)
=123.5÷13
=9.5(元)
答:平均每支钢笔9.5元。
每一份努力,都将在学习中得到最好的回报。加油!
人教版五年级数学上册
第三单元:小数除法单元复习专题
掌握小数除法的计算方法,并能正确地进行计算;能根据算式的特点合理选择计算方法,体会转化的数学思想。
掌握用“四舍五入”法取商的近似数,能根据实际情况合理运用“进一法”和“去尾法”取商的近似数。
认识循环小数、有限小数和无限小数;能借助计算器探索规律,并应用规律解决问题,提高学生自主探究问题的能力。
掌握小数除法的计算方法;能正确地进行小数除法的笔算和简便计算;能正确应用“四舍五入”法取商的近似数。
掌握确定小数除法中商的小数点位置的方法;会把除数是小数的除法转化成除数是整数的除法,并能正确地进行计算。
小数除法
除数是整数的小数除法
计算法则
除到被除数的末尾有余数
整数部分不够商1
一个数除以小数
计算法则
被除数的小数位数比除数少
商的近似数
用“四舍五入”法取商的近似数
循环小数
意义
循环节
有限小数、无限小数
解决问题
用“进一法”解决实际问题
用“去尾法”解决实际问题
用计算器探索规律
知识点01:除数是整数的小数除法
1、除数是整数的小数除法计算法则:
(1)小数除以整数,按照整数除法的方法去除;
(2)商的小数点要和被除数的小数点对齐;
(3)除得的商的哪一位不够商1,就在那一位上写0,再继续除;
(4)如果除到被除数的末尾仍有余数,就在余数的后面添0再除。
【例1】列竖式计算。
(1)25.8÷3= (2)2.03÷7=
25.8
3
.
8
24
6
8
18
0
1
8.6
0.29
2.03
7
.
0
14
9
3
63
0
6
2
商的哪一位不够商1,就在那一位上写0。
【例1】列竖式计算。
(3)30.5÷5= (4)6.57÷9=
30.5
5
.
6
30
1
5
5
0
6.1
0.73
6.57
9
.
0
63
3
7
27
0
2
7
【例2】31.2是( ) 的6倍。
A、5.2 B、6.7 C、187.2
求31.2是多少的6倍,根据已知一个数的几倍是多少,求这个数,用除法计算。
31.2÷6=5.2
A
【例3】“妈妈买了4千克水果,共用去了26.8元,每千克水果多少元?”图中竖式中箭头所指“28”表示( )。
A、28元 B、28千克
C、2.8元 D、2.8千克
箭头所指的“28”中的“8”对应的是十分位,代表28个0.1元。28×0.1=2.8,所以竖式中箭头所指“28”表示2.8元。
C
【例4】一艘货轮从港口出发,3小时航行160.8千米,平均每小时航行多少千米?
【解析】根据速度=路程÷时间,代入数值计算即可。
【解答】
160.8÷3=53.6(千米)
答:平均每小时航行53.6千米。
【例5】李阿姨去超市买了2盒巧克力和3袋面包。一共花了63.8元,一袋面包8.8元。一盒巧克力多少元?
【解析】先根据总价=单价×数量,用一袋面包的价钱乘以袋数,算出3袋面包的价钱;然后用总价钱减去面包的价钱得到巧克力的总价钱;再根据单价=总价÷数量,用巧克力的总价钱除以盒数,得到一盒巧克力的价钱。
【例5】李阿姨去超市买了2盒巧克力和3袋面包。一共花了63.8元,一袋面包8.8元。一盒巧克力多少元?
【解答】
(63.8-8.8×3)÷2
=(63.8-26.4)÷2
=37.4÷2
=18.7(元)
答:一盒巧克力18.7元。
知识点02:一个数除以小数
1、一个数除以小数计算法则:
(1)先明确除数有几位小数,再移动除数的小数点,使它变成整数;
(2)除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数的末尾用“0”补足);
(3)然后按照除数是整数的小数除法进行计算。
2、小数除法的验算方法:计算小数除法也可以用乘法来验算。
【例6】列竖式计算:
(1)83.2÷2.6= (2)0.936÷0.18=
83.2
2.6
3
2
5
2
52
0
78
32
0.936
0.18
5
.
2
3
6
36
90
0
.
5.2
【例6】列竖式计算:
(3)51.7÷2.5= (4)38.7÷3.6=
20.68
51.7
2.5
2
.
0
1
6
7
50
0
150
20
0
8
200
0
位数不够的,在被除数的末尾用“0”补足。
10.75
38.7
3.6
1
.
0
2
7
7
36
0
252
18
0
5
180
0
【例7】一台普通洗衣机一次的用水量是2.73立方米,一台节水洗衣机一次的用水量是1.3立方米。一台普通洗衣机一次的用水量是一台节水洗衣机的几倍?
【解析】根据求一个数是另一个数的几倍,用除法。用普通洗衣机的用水量除以节水洗衣机的用水量即可。
【解答】
2.73÷1.3=2.1
答:一台普通洗衣机一次的用水量是一台节水洗衣机的2.1倍。
【例8】一个服装厂做一套衣服原来需要2.6米的布料,后来改进裁剪方法,每套只需2.2米的布料。原来准备做220套衣服的布料,现在可以做多少套?
【解析】先用做一套衣服原来需要的布料长度乘衣服套数,算出原来准备的布料总量,再除以现在每套衣服所需的布料量,就可得到现在能做的套数。
【例8】一个服装厂做一套衣服原来需要2.6米的布料,后来改进裁剪方法,每套只需2.2米的布料。原来准备做220套衣服的布料,现在可以做多少套?
【解答】
2.6×220÷2.2
=572÷2.2
=260(套)
答:现在可以做260套。
【例9】5台同样的起重机同时工作3.2小时,可以吊运货物20.8吨,照这样计算,一台起重机每小时可以吊运货物多少吨?
【解析】已知5台同样的起重机同时工作3.2小时可以吊运货物16吨,先用吊运货物的吨数除以时间,算出5台起重机1小时吊运货物的吨数;再用5台起重机1小时吊运货物的吨数除以起重机台数,求出1台起重机每小时吊运货物的吨数。
【例9】5台同样的起重机同时工作3.2小时,可以吊运货物20.8吨,照这样计算,一台起重机每小时可以吊运货物多少吨?
【解答】
20.8÷3.2÷5
=6.5÷5
=1.3(吨)
答:一台起重机每小时可以吊运货物1吨。
知识点03:商的近似数
1、求商的近似数时,要除到比要保留的小数位数多一位,然后按照“四舍五入”法取商的近似数。
2、注意
用“四舍”法取商的近似数,商小于准确数;
用“五入”法取商的近似数,商大于准确数
【例10】17.07÷3的商保留一位小数是( )。
除数是整数的小数除法,按照整数除法进行计算,商的小数点要与被除数的小数点对齐,被除数的数用完时,在被除数的末尾添0”继续除。
要求得数保留几位小数,要除到它的下一位,再用四舍五入的方法取商的近似数。
17.07÷3=5.69≈5.7
5.7
【例11】下面算式中,计算结果不可能是10.86的是( )。
A、1.□□×6 B、3.□□×3 C、6.□□×2
根据积÷一个因数=另外一个因数,用10.28除以每个选项中已知的因数,和另外一个因数进比较即可。
A中,10.28÷6=1.81,符合题意;
B中,10.86÷3=3.62,符合题意;
C中,10.86÷2=5.43,不符合题意;
C
【例12】甲、乙、丙三人加工同样多的零件。甲3小时完成11个,乙2小时完成9个,丙4小时完成13个,平均每小时( )做得最多。
用加工零件个数除以时间,分别求出几人每小时加工的零件个数,比较即可。
11÷3≈3.7 (个)
9÷2=4.5 (个)
13÷4≈3.3 (个)
3.3<3.7<4.5
所以每小时乙做得最多。
乙
【例13】妈妈去市场买了一大袋土豆,共重4千克。已知19个土豆约重2.5千克,估一估,这袋土豆约有( )。
A、40个以上 B、不到20个 C、30个左右
土豆个数÷相应千克数=每千克土豆的个数,每千克土豆的个数×总质量=土豆总个数,据此列式。
19÷2.5×4
=7.6×4
=30.4
≈30(个)
C
知识点04:循环小数
1、循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
2、循环节:一个循环小数的小数部分,依次不断重复出现的数字,就是这个循环小数的循环节。
3、有限小数:小数部分的位数有限的小数;
无限小数:小数部分的位数无限的小数。
4、循环小数一定是无限小数。
【例14】下列除法算式中,结果是循环小数的是( )。
A、5÷2.1 B、3.8÷6 C、9÷1.6
循环小数是指一个数的小数部分从某一位起,一个或几个数字依次重复出现的无限小数。
A选项,5÷2.1=2.38095……不是循环小数;
B选项,3.8÷6=0.63333……是循环小数;
C选项,9÷1.6=5.625是有限小数。
A
【例15】下面循环小数中,最大的是( )。
A、 B、 C、
先看整数部分,整数部分大的那个数就大;整数部分相同,十分位上的数大的那个数就大;十分位上的数相同,百分位上的数大的那个数就大……以此类推。
A选项,=0.2399999……
B选项,=0.268268268……
C选项,=0.2575757……
所以> >
B
【例16】已知9÷3.3的结果是一个循环小数,这个循环小数的小数点右边第29位的数字是( )。
9÷3.3=,商的循环节是72,每2个数字一循环;29÷2=14……1,余数是1表示是一个循环里的第一个数,即7。所以这个循环小数的小数点右边第29位的数字是7。
7
知识点05:解决问题
1、进一法:在取近似数时,不管省略部分首位上的数字是儿,都要向前一位进一。
2、去尾法:在取近似数时,不管省略部分首位上的数字是儿,都要全部舍去。
3、要根据实际情况选择用“进一法”还是“去尾法”。
用去尾法得到的近似数比准确数小。
用进一法得到的近似数比准确数大。
【例17】有一批重30吨的货物,如果用一辆限载3.2吨的货车运送,运完这批货物至少需要运( )次。
用货物的总重量除以货车的限载重量,求出运送的次数。根据实际情况,对计算结果采用“进一法”,需要再加一次运输。
30÷3.2=9.375≈10
答:张叔叔运完这批货物至少需要运10次。
10
【例18】一个箱子最多能装物品8千克,要装完86千克物品,至少需要多少个这样的箱子?
【解析】先用总物品重量除以每个箱子能装的重量,计算所需箱子的数量。结果要采用“进一法”取整,那么余下的物品也需要一个箱子。
【解答】
86÷8=10.75(个)
答:至少需要11个这样的箱子。
【例19】李叔叔用3.85米铁丝做衣架,每个衣架用0.7米铁丝。最多能做多少个?
【解析】已知铁丝的总长度和做一个衣架所需铁丝的长度,要求最多能做多少个衣架,就是求总长度里有多少个单个衣架所需的长度,用除法计算。计算结果如果有小数,因为衣架个数必须是整数,所以采用去尾法保留整数。
【解答】
3.85÷0.7=5.5(个)
答:最多能做5个。
【例20】一块长方形的铁皮长4.85米,宽2.9米,如果做一个铁箱需要用铁皮3.2平方米,这块铁皮最多可以做几个铁箱?
【解析】先根据长方形面积=长×宽计算铁皮的总面积,再用总面积除以做一个铁箱所需的铁板面积,得到的商就是能做的铁箱数量,因为铁箱个数只能为整数,所以采用去尾法保留整数。
【解答】4.8×2.9=13.92(平方米)
13.92÷3.2=4.35≈4(个)
答:这块铁皮最多可以做4个铁箱。
1、一个数的3倍是4.5,这个数是( )。
A、13.5 B、5.5 C、1.5
2、15.69÷2.5的商保留倒百分位是( )。
A、6.27 B、6.28 C、6.29
C
B
3、9.6666666是一个( ) 。
A、有限小数 B、无限小数 C、循环小数
4、在一道没有余数的除法算式里,被除数、除数和商的和是20.6,被除数是除数的5倍。除数是( )。
A
2.6
5、两人去书店买笔,明明买了8支钢笔,亮亮买了同样的5支钢笔,一共花了123.5元,那么平均每支钢笔多少元?
123.5÷(8+5)
=123.5÷13
=9.5(元)
答:平均每支钢笔9.5元。
每一份努力,都将在学习中得到最好的回报。加油!
