人教版2024-2025学年八年级数学上册举一反三专题11.3三角形的内角和定理【十大题型】(学生版+解析)
文档属性
| 名称 | 人教版2024-2025学年八年级数学上册举一反三专题11.3三角形的内角和定理【十大题型】(学生版+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 11:43:48 | ||
图片预览




文档简介
专题11.3 三角形的内角和定理【十大题型】
【人教版】
【题型1 证明三角形内角和】 1
【题型2 由三角形内角和直接求角度】 3
【题型3 由三角形内角和判断三角形形状】 4
【题型4 三角形内角和与平行线的综合运用】 4
【题型5 三角形内角和与翻折的综合运用】 5
【题型6 三角形内角和与角平分线的综合运用】 7
【题型7 三角形内角和与三角板的综合运用】 8
【题型8 由三角形内角和定理探究角度之间的关系】 9
【题型9 由直角三角形的性质求角度】 11
【题型10 锐角互余的三角形是直角三角形】 12
知识点1:三角形的内角和定理
(1)三角形内角和定理:三角形三个内角的和等于.
(2)因为三角形三个内角的和等于,所以任何一个三角形中至少有两个锐角,最多有一个钝角或直角.
【提示】(1)三角形内角和定理适用于任意三角形.
(2)任何一个三角形中,至少有两个锐角,最多有一个钝角或直角.
【题型1 证明三角形内角和】
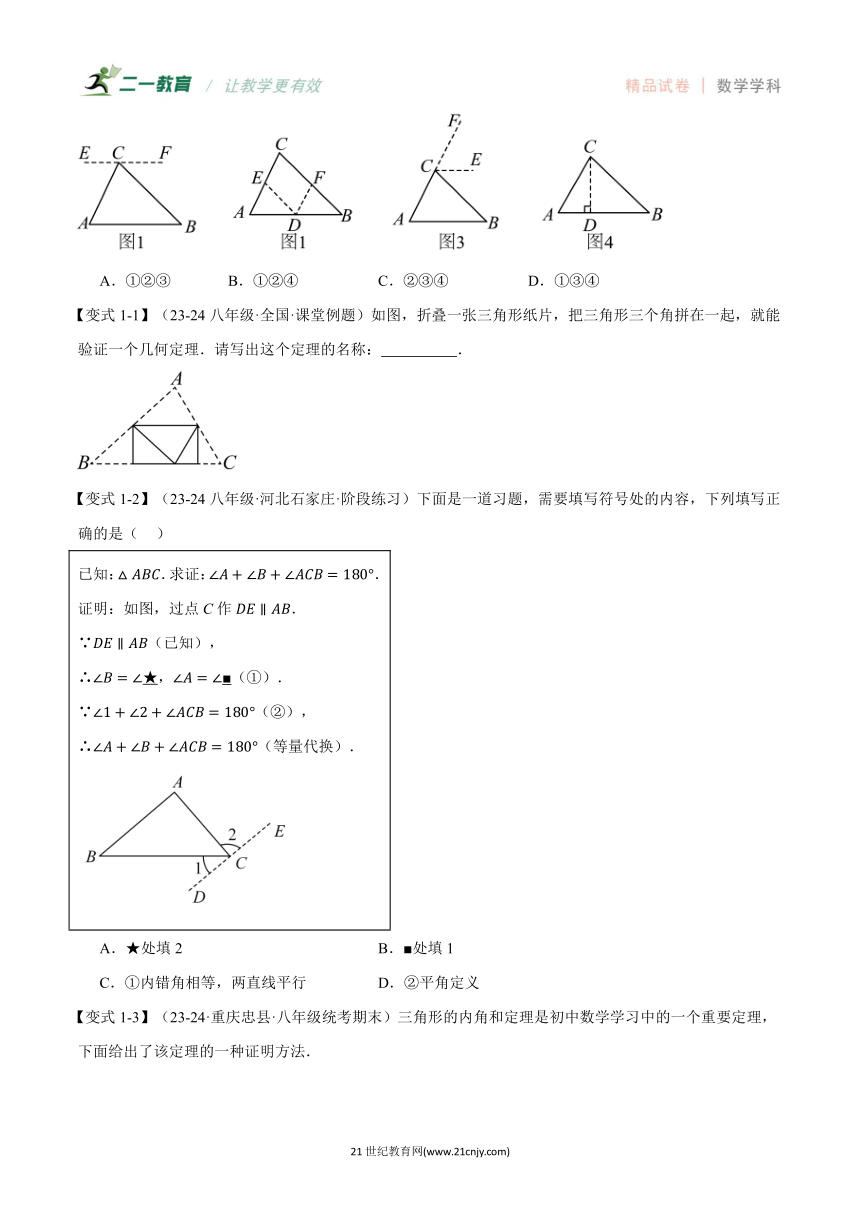
【例1】(23-24八年级·河北邢台·阶段练习)在探究证明“三角形的内角和是”时,综合实践小组的同学作了如下四种辅助线,其中能证明“三角形的内角和是”的有( )
①如图1,过点C作;
②如图2,过上一点D分别作,;
③如图3,延长到点F,过点C作;
④如图4,过点C作于点D.
A.①②③ B.①②④ C.②③④ D.①③④
【变式1-1】(23-24八年级·全国·课堂例题)如图,折叠一张三角形纸片,把三角形三个角拼在一起,就能验证一个几何定理.请写出这个定理的名称: .
【变式1-2】(23-24八年级·河北石家庄·阶段练习)下面是一道习题,需要填写符号处的内容,下列填写正确的是( )
已知:.求证:. 证明:如图,过点C作. ∵(已知), ∴★,■(①). ∵(②), ∴(等量代换).
A.★处填2 B.■处填1
C.①内错角相等,两直线平行 D.②平角定义
【变式1-3】(23-24·重庆忠县·八年级统考期末)三角形的内角和定理是初中数学学习中的一个重要定理,下面给出了该定理的一种证明方法.
已知:如图, . 求证:. 证明:作的延长线,在外部,以为一边,作. 所以,(内错角相等,两直线平行). 所以,( ). 因为,,,组成一个平角, 所以,(平角的定义), 所以,( ).
(1)请将上面的“已知”和推理“依据”补充完整;
(2)该定理有多种证明方法,请再写出一种证明方法.
【题型2 由三角形内角和直接求角度】
【例2】(23-24八年级·江苏宿迁·期末)如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.若为倍角三角形,,则 .
【变式2-1】(23-24八年级·新疆巴音郭楞·期末)如图1是某款婴儿手推车,如图2是其侧面的示意图,若,,,则的度数为 .
【变式2-2】(23-24八年级·福建宁德·期末)将沿方向平移得到.若,,则的度数是( )
A. B. C. D.
【变式2-3】(23-24八年级·江苏宿迁·期末)已知:如图,在四边形中,点在上,与互余,且,试猜想与的位置关系,并说明理由.
【题型3 由三角形内角和判断三角形形状】
【例3】(23-24八年级·河北廊坊·期中)如图,当时,该三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
【变式3-1】(23-24八年级·广西梧州·期中)中,若,则的形状是( )
A.锐角三角形 B.直角三角形 C.钝角二角形 D.无法确定
【变式3-2】(23-24八年级·安徽淮北·阶段练习)如果一个三角形的两个内角都小于30°,那么这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
【变式3-3】(23-24八年级·重庆秀山·期中)中,,请判断三角形的形状并证明.
【题型4 三角形内角和与平行线的综合运用】
【例4】(23-24八年级·河南平顶山·期末)如图,△CEF中,∠E=70°,∠F=50°,且AB∥CF ,AD∥CE,连接BC,CD,则∠A的度数是( )
A.40° B.45° C.50° D.60°
【变式4-1】(23-24八年级·四川成都·期末)如图,ABCD,AC与BD相交于点O,若∠A=25°,∠D=45°,则∠AOB的大小为( )
A.90° B.110° C.120° D.135°
【变式4-2】(23-24八年级·陕西渭南·期中)如图,在三角形中,点D,H,E分别是边,,上的点,连接,,F为上一点,连接,若,,.则的度数为 .
【变式4-3】(23-24八年级·湖北孝感·期中)如图,直线,点A,B分别是,上的动点,点G在上,,和的角平分线交于点D,若,则m的值为 .
【题型5 三角形内角和与翻折的综合运用】
【例5】(23-24八年级·江苏扬州·期末)如图,、是边、上的点,沿翻折后得到,沿翻折后得到,且点在边上,沿翻折后得到,且点在边上,若,则( )
A. B. C. D.
【变式5-1】(23-24八年级·江苏连云港·期中)如图,将直角三角形纸片沿(D是斜边上一点)折叠,使点B落在点处,若,则的度数是 °.(用含的代数式表示)
【变式5-2】(23-24八年级·广西南宁·期中)如图,在折纸活动中,小李制作了一张的纸片,点,分别在边,上,将沿着折叠压平,与重合,若,则 .
【变式5-3】(23-24八年级·福建漳州·期中)如图,在中,,,D是线段上一个动点,连接,把沿折叠,点C落在同一平面内的点E处,当平行于的边时,的度数为 .
【题型6 三角形内角和与角平分线的综合运用】
【例6】(23-24八年级·江苏淮安·期末)如图,中,,,平分,于D,,则的度数 .
【变式6-1】(23-24八年级·江苏徐州·期中)如图,、是的角平分线,与交于点,, (用含的代数式表示).
【变式6-2】(23-24八年级·辽宁营口·期中)如图,中,是边上的高,分别是、的平分线, ,,则( ).
A. B. C. D.
【变式6-3】(23-24八年级·江苏苏州·期中)新定义:在中,若存在一个内角是另外一个内角度数的n倍(n为大于1的正整数),则称为n倍角三角形.例如,,可知,所以为2倍角三角形.
(1)在中,,则为 倍角三角形.
(2)如图1,直线与直线相交于O,;已知、的角平分线交于点C,在中,在中,如果有一个角是另一个角的2倍,请求出的度数.
(3)如图2,直线⊥直线于点O,点A、点B分别在射线上,已知、的角平分线分别与的角平分线所在的直线交于点、.若为3倍角三角形,试求的度数.
【题型7 三角形内角和与三角板的综合运用】
【例7】(23-24八年级·江西南昌·期末)将一副三角板的直角顶点重合按如图放置,,,小明得到下列结论:
①如果,则;
②;
③如果,则;
④如果,则.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【变式7-1】(23-24八年级·安徽六安·期末)生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,将一副学生用三角板按如图所示的方式放置.若,则的度数是 .
【变式7-2】(23-24八年级·河北唐山·期末)如图,将一副三角板的直角顶点重合,且使,则的度数是( )
A. B. C. D.
【变式7-3】(23-24八年级·湖北随州·期末)将一副学生用的三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)如图叠放,则下列4个结论中正确的个数有( )
①∠AOC+∠BOD=90°;②∠AOC=∠BOD;③∠AOC-∠CEA=15°;④如果OB平分∠DOC,则OC平分∠AOB
A.0 B.1 C.2 D.3
【题型8 由三角形内角和定理探究角度之间的关系】
【例8】(23-24八年级·全国·单元测试)如图1,已知线段相交于点,连接,则我们把形如这样的图形称为“8字型”.
(1)求证:;
(2)如图2,若和的平分线、相交于点,且与分别相交于点.
①以线段为边的“8字型”有__________个,以点为交点的“8字型”有__________个;
②若,求的度数;
③若角平分线中角的关系改为,试探究与之间存在的数量关系,并证明理由.
【变式8-1】(23-24八年级·江苏南京·期末)如图,中,,点、分别在边、上,,则下面关于与的关系中一定正确的是( )
A. B.
C. D.
【变式8-2】(23-24八年级·江西南昌·期中)已知如图,在中,,分别是的高和角平分线,若,
(1)求的度数.
(2)求与,的关系,并说明理由.
【变式8-3】(23-24八年级·江苏连云港·期末)如图1,过直线外一点作,连接,,的平分线与交于点,点是线段上一动点(不与重合),连接.
(1)若,则_____________°,________________°;
(2)若,求证:;
(3)如图2,的平分线与交于点,连接,若,,试求之间的等量关系.
知识点2:直角三角形的性质与判定
(1)直角三角形的两个锐角互余.
(2)有两个角互余的三角形是直角三角形.
【提示】直角三角形的性质和判定的应用思路:
(1)见直角三角形,可得两锐角互余.
(2)见两角互余,可得直角三角形.
【题型9 由直角三角形的性质求角度】
【例9】(23-24八年级·河南郑州·期中)在直角三角形中,比的3倍还多,则的大小为 .
【变式9-1】(23-24八年级·河南南阳·期末)一副三角板按如图所示放置,点在上,点在上,若,则 .
【变式9-2】(23-24八年级·湖南株洲·期中)如图,在中,,,于D,于E,与交于H,则 .
【变式9-3】(23-24八年级·四川成都·期末)如图,有一副三角板ABC与DEF,其中∠C=∠F=90°,∠A=60°,∠D=45°,在一平面内将这副三角板进行拼摆,使得点B、E重合,且点B、C、F三点在同一直线上,则∠ABD的度数是 °.
【题型10 锐角互余的三角形是直角三角形】
【例10】(23-24八年级·全国·课堂例题)如图,在中,是边上的高,E是边上一点,交于点M,且.求证:是直角三角形.
【变式10-1】(23-24八年级·江苏南京·期中)证明:有两个角互余的三角形是直角三角形.
已知:如图, ,
求证: .
证明:
【变式10-2】(23-24八年级·河南周口·阶段练习)在下列条件中:①,②,③,④中,能确定是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
【变式10-3】(23-24八年级·全国·课后作业)如图,平分,平分,和交于点E.写出图中所有的直角三角形(不要求证明).
21世纪教育网(www.21cnjy.com)
专题11.3 三角形的内角和定理【十大题型】
【人教版】
【题型1 证明三角形内角和】 1
【题型2 由三角形内角和直接求角度】 6
【题型3 由三角形内角和判断三角形形状】 8
【题型4 三角形内角和与平行线的综合运用】 10
【题型5 三角形内角和与翻折的综合运用】 13
【题型6 三角形内角和与角平分线的综合运用】 18
【题型7 三角形内角和与三角板的综合运用】 22
【题型8 由三角形内角和定理探究角度之间的关系】 26
【题型9 由直角三角形的性质求角度】 33
【题型10 锐角互余的三角形是直角三角形】 37
知识点1:三角形的内角和定理
(1)三角形内角和定理:三角形三个内角的和等于.
(2)因为三角形三个内角的和等于,所以任何一个三角形中至少有两个锐角,最多有一个钝角或直角.
【提示】(1)三角形内角和定理适用于任意三角形.
(2)任何一个三角形中,至少有两个锐角,最多有一个钝角或直角.
【题型1 证明三角形内角和】
【例1】(23-24八年级·河北邢台·阶段练习)在探究证明“三角形的内角和是”时,综合实践小组的同学作了如下四种辅助线,其中能证明“三角形的内角和是”的有( )
①如图1,过点C作;
②如图2,过上一点D分别作,;
③如图3,延长到点F,过点C作;
④如图4,过点C作于点D.
A.①②③ B.①②④ C.②③④ D.①③④
【答案】A
【分析】本题主要考查三角形内角和的定理的证明,平行线的性质,熟练掌握转化的思想以及平角的定义是解决本题的关键.运用转化的思想作出相应的平行线,把三角形的内角进行转化,再根据平角的定义逐一判断即可得答案.
【详解】①∵,
∴,
∵,
∴,故①符合题意,
②∵,,
∴,,
∴,
∵,
∴,故②符合题意,
③∵,
∴,
∵,
∴,故③符合题意,
④ ,
,
不能证明“三角形的内角和等于”故④不符合题意,
故选:A.
【变式1-1】(23-24八年级·全国·课堂例题)如图,折叠一张三角形纸片,把三角形三个角拼在一起,就能验证一个几何定理.请写出这个定理的名称: .
【答案】三角形内角和定理
【分析】根据折叠前后的两个角相等,把三角形的三个角转化为一个平角,可以得到三角形内角和定理.
【详解】解:根据折叠的性质,,
∵,
∴,
∴定理为:三角形内角和定理.
故答案为:三角形内角和定理.
【点睛】本题主要考查了三角形的内角和定理的证明,熟练掌握翻折变换的性质是解题的关键.
【变式1-2】(23-24八年级·河北石家庄·阶段练习)下面是一道习题,需要填写符号处的内容,下列填写正确的是( )
已知:.求证:. 证明:如图,过点C作. ∵(已知), ∴★,■(①). ∵(②), ∴(等量代换).
A.★处填2 B.■处填1
C.①内错角相等,两直线平行 D.②平角定义
【答案】D
【分析】根据题意结合平行线的性质进行证明判断即可.
【详解】证明:如图,过点C作.
∵(已知),
∴1,2(两直线平行,内错角相等).
∵(平角定义),
∴(等量代换).
故选D
【点睛】本题主要考查了三角形内角和定理的证明,平行线的性质,正确理解题意是解题的关键.
【变式1-3】(23-24·重庆忠县·八年级统考期末)三角形的内角和定理是初中数学学习中的一个重要定理,下面给出了该定理的一种证明方法.
已知:如图, . 求证:. 证明:作的延长线,在外部,以为一边,作. 所以,(内错角相等,两直线平行). 所以,( ). 因为,,,组成一个平角, 所以,(平角的定义), 所以,( ).
(1)请将上面的“已知”和推理“依据”补充完整;
(2)该定理有多种证明方法,请再写出一种证明方法.
【答案】(1)、、是的三个内角;两直线平行,同位角相等;等量代换
(2)见解析
【分析】本题考查了三角形内角和定理,平行线的判定与性质:
(1)在外部,以为一边,作.根据平行线的判定与性质及平角定义求解即可;
(2)过点A作,根据平行线的性质°,由此证明即可.
【详解】(1)解:已知:如图,、、是的三个内角.
求证:.
证明:如图,作的延长线,在外部,以为一边,作.
所以,(内错角相等,两直线平行).
所以,(两直线平行,同位角相等).
因为,组成一个平角,
所以,(平角的定义),
所以,(等量代换).
(2)证明:如图,过点A作,
∵,
∴(两直线平行,内错角相等).
(两直线平行,同旁内角互补).
即.
∴.
【题型2 由三角形内角和直接求角度】
【例2】(23-24八年级·江苏宿迁·期末)如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.若为倍角三角形,,则 .
【答案】或或或
【分析】该题主要考查了三角形内角和定理,解题的关键是分类讨论.
根据“倍角三角形”定义分为当时,当时,当时,当时,结合三角形内角和定理求解即可;
【详解】解:当时,;
当时,,;
当时,,解得:;
当时,,解得:;
故答案为:或或或.
【变式2-1】(23-24八年级·新疆巴音郭楞·期末)如图1是某款婴儿手推车,如图2是其侧面的示意图,若,,,则的度数为 .
【答案】/85度
【分析】本题考查平行线的性质和三角形内角和定理,根据平行线的性质可得,利用三角形内角和定理得出的度数,即可求解.
【详解】解:如图,
∵,
∴,
∵
∴,
∴
∴,
故答案为:.
【变式2-2】(23-24八年级·福建宁德·期末)将沿方向平移得到.若,,则的度数是( )
A. B. C. D.
【答案】B
【分析】本题考查了平移的性质,掌握平移的性质是解题的关键.根据图形平移,图形的大小不变,对应角、对应边相等即可求解.
【详解】解:根据题意,由平移的性质得:,
∴,
故选:B .
【变式2-3】(23-24八年级·江苏宿迁·期末)已知:如图,在四边形中,点在上,与互余,且,试猜想与的位置关系,并说明理由.
【答案】,理由见解析
【分析】本题考查了垂线的定义,余角的定义,三角形内角和定理,根据,推出,进而得到,由,得到,从而得到,推出.
【详解】解:,理由见如下:
,
,
,
,
,
,
.
【题型3 由三角形内角和判断三角形形状】
【例3】(23-24八年级·河北廊坊·期中)如图,当时,该三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
【答案】B
【分析】本题考查了三角形内角和定理,三角形的分类.利用三角形内角和定理得到,结合已知计算即可求解.
【详解】解:如图,且,
∴,
∴,
∴,
∴该三角形的形状是直角三角形,
故选:B.
【变式3-1】(23-24八年级·广西梧州·期中)中,若,则的形状是( )
A.锐角三角形 B.直角三角形 C.钝角二角形 D.无法确定
【答案】B
【分析】本题主要考查三角形内角和定理,根据在中,,可求出的度数,即可得出结论,熟知三角形内角和是是解答本题的关键.
【详解】解:∵在中,,
∴,
∵,
∴,
∴,
∴是直角三角形.
故选:B.
【变式3-2】(23-24八年级·安徽淮北·阶段练习)如果一个三角形的两个内角都小于30°,那么这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
【答案】C
【分析】根据三角形的内角和定理即可得到结论.
【详解】解:∵三角形的两个内角都小于30°,
∴这两个内角的和小于60°,
∵三个内角的和为180°,
∴另一个角大于120°,
∴这个三角形是钝角三角形,
故选:C.
【点睛】本题考查了三角形的内角和定理,熟练掌握三角形的内角和定理是解题的关键.
【变式3-3】(23-24八年级·重庆秀山·期中)中,,请判断三角形的形状并证明.
【答案】是直角三角形,证明见解析
【分析】本题主要考查了三角形内角和定理,设,根据三角形内角和为180度建立方程,解方程求出x的值,进而求出,由此可得结论.
【详解】解;是直角三角形,证明如下;
∵,
∴可设,
∵,
∴,
解得,
∴,
∴是直角三角形.
【题型4 三角形内角和与平行线的综合运用】
【例4】(23-24八年级·河南平顶山·期末)如图,△CEF中,∠E=70°,∠F=50°,且AB∥CF ,AD∥CE,连接BC,CD,则∠A的度数是( )
A.40° B.45° C.50° D.60°
【答案】D
【分析】连接AC并延长交EF于点M.由平行线的性质得,,再由等量代换得,先求出即可求出.
【详解】连接AC并延长交EF于点M.
∵,
∴,
∵,
∴,
∴,
∵,
∴,
故选D.
【点睛】本题主要考查了平行线的性质以及三角形的内角和定理,属于基础题型.
【变式4-1】(23-24八年级·四川成都·期末)如图,ABCD,AC与BD相交于点O,若∠A=25°,∠D=45°,则∠AOB的大小为( )
A.90° B.110° C.120° D.135°
【答案】B
【分析】首先根据两直线平行,内错角相等得出∠B=∠D=45°,然后由△AOB的内角和为180°,求出∠AOB的大小.
【详解】解:∵ABCD,
∴∠B=∠D=45°.
∵∠A+∠AOB+∠B=180°,
∴∠AOB=180°﹣25°﹣45°=110°.
故选:B.
【点睛】本题考查了平行线的性质及三角形的内角和定理,根据平行线的性质得出∠B=∠D=45°是解题的关键,属于基础题型,比较简单.
【变式4-2】(23-24八年级·陕西渭南·期中)如图,在三角形中,点D,H,E分别是边,,上的点,连接,,F为上一点,连接,若,,.则的度数为 .
【答案】
【分析】由,,得到,根据平行线的判定,得到,根据平行线的性质,得到,根据三角形内角和定理,求出的度数,即可求解,
本题考查了,平行线的性质与判定,三角形内角和定理,解题的关键是:熟练掌握相关性质定理.
【详解】解:∵,,
∴,
∴,
∴,
∵,
∴,
故答案为:.
【变式4-3】(23-24八年级·湖北孝感·期中)如图,直线,点A,B分别是,上的动点,点G在上,,和的角平分线交于点D,若,则m的值为 .
【答案】76
【分析】先由平行线的性质得到,再根据三角形内角和定理和角平分线的定义求出m的值.
【详解】解:过点C作,
,
,,
,
,
,
,
由题意可得为的角平分线,为的角平分线,
,,
,,
,
,
,
.
故答案为:76.
【点睛】本题考查了平行线的性质和三角形内角和定理,熟练掌握平行线的性质和三角形内角和定理是解题的关键.
【题型5 三角形内角和与翻折的综合运用】
【例5】(23-24八年级·江苏扬州·期末)如图,、是边、上的点,沿翻折后得到,沿翻折后得到,且点在边上,沿翻折后得到,且点在边上,若,则( )
A. B. C. D.
【答案】D
【分析】本题考查了折叠的性质,三角形的内角和定理.根据折叠的性质以及三角形内角和定理得出,,将已知数据代入,即可求解.
【详解】解:如图所示,
依题意,,
∴
,
即,
,,
∵,
∴,
∴,
∴,
∴,
故选:D.
【变式5-1】(23-24八年级·江苏连云港·期中)如图,将直角三角形纸片沿(D是斜边上一点)折叠,使点B落在点处,若,则的度数是 °.(用含的代数式表示)
【答案】
【分析】本题考查了三角形折叠中的角度问题,根据角度间关系可得,再根据折叠性质得到,最后推出,即可得出答案,理清角度间的数量关系是解题关键.
【详解】解:,
,
将直角三角形纸片沿(D是斜边上一点)折叠,使点B落在点处,
,
,
,
,
.
故答案为:.
【变式5-2】(23-24八年级·广西南宁·期中)如图,在折纸活动中,小李制作了一张的纸片,点,分别在边,上,将沿着折叠压平,与重合,若,则 .
【答案】/65度
【分析】本题考查折叠的性质,三角形内角和定理.由折叠可得,,进而可得,结合,可得,即可求解.
【详解】解:将沿着折叠压平,与重合,
,,
,
,
,
,
,
,
故答案为:.
【变式5-3】(23-24八年级·福建漳州·期中)如图,在中,,,D是线段上一个动点,连接,把沿折叠,点C落在同一平面内的点E处,当平行于的边时,的度数为 .
【答案】或
【分析】本题考查了平行线的性质,折叠问题,三角形的内角和等知识点,分两种情况,和,分别画出图形,再利用平行线的性质求解即可,正确分类并画出图形是解题的关键.
【详解】由折叠的性质得:,
设,
∵,
∴,
由题意,分以下两种情况:
如图,当时,
∵,
∴,
∵,
∴,
解得,
即;
如图,当时,
∴,
∵,
∴,
解得,
即,
综上,的大小为或.
故答案为:或.
【题型6 三角形内角和与角平分线的综合运用】
【例6】(23-24八年级·江苏淮安·期末)如图,中,,,平分,于D,,则的度数 .
【答案】
【分析】本题考查了三角形的内角和以及角平分线的定义,熟练掌握三角形的内角和以及角平分线的定义是解题的关键.首先根据三角形的内角和定理求得的度数,根据角平分线的定义求得的度数,则可以求解,然后在中,利用内角和定理即可求得的度数.
【详解】,,
,
平分,
,
,
,
,
,
,
,
.
故答案为:.
【变式6-1】(23-24八年级·江苏徐州·期中)如图,、是的角平分线,与交于点,, (用含的代数式表示).
【答案】
【分析】此题考查了与角平分线有关的三角形内角和定理,先求出,再利用角平分线求出,再利用三角形内角和定理即可求出答案.
【详解】解:∵,
∴,
∵、是的角平分线,
∴,
∴,
∵,
∴,
故答案为:
【变式6-2】(23-24八年级·辽宁营口·期中)如图,中,是边上的高,分别是、的平分线, ,,则( ).
A. B. C. D.
【答案】A
【分析】此题考查了三角形内角和定理及角平分线的性质,依据是边上的高,,即可得到,依据 ,平分,即可得到,再依据是的平分线,得到,可得,熟练掌握三角形内角和定理以及角平分线定义的运用是解题的关键.
【详解】解:∵是边上的高,
∴,
∵,
∴,
∵,平分,
∴,
∴,
∵是的平分线,
∴,
∴
故选:.
【变式6-3】(23-24八年级·江苏苏州·期中)新定义:在中,若存在一个内角是另外一个内角度数的n倍(n为大于1的正整数),则称为n倍角三角形.例如,,可知,所以为2倍角三角形.
(1)在中,,则为 倍角三角形.
(2)如图1,直线与直线相交于O,;已知、的角平分线交于点C,在中,在中,如果有一个角是另一个角的2倍,请求出的度数.
(3)如图2,直线⊥直线于点O,点A、点B分别在射线上,已知、的角平分线分别与的角平分线所在的直线交于点、.若为3倍角三角形,试求的度数.
【答案】(1)3
(2)或或或
(3)或
【分析】本题考查三角形的内角和定理,余角的意义等知识,读懂新定义倍角三角形的意义和分类讨论是解决问题的基础和关键.
(1)由,可知,再根据倍角三角形的定义可得结论.
(2)先求出,,然后分四种情形分别求解即可.
(3)先证明,,然后分四种情形分别求解即可.
【详解】(1),,
,
,
为3倍角三角形,
故答案为:3;
(2)解:∵,
∴.
又∵平分,平分,
∴,
∴.
①当时,
∵,
∴;
②当时,
∵,
∴;
③当时,
∵,
∴;
④当时,
∵,
∴,
∴.
综上,在中当一个角是另一个角的2倍时,等于或或或;
(3)平分,平分,
,,
,
;
又平分,
①,
②;
得:.
若为3倍角三角形:
若,
,
,
;
若,
,
(不符合题意,舍去);
若,
,
;
若,
,,
(不符合题意,舍去);
综上所述,等于或时,为3倍角三角形.
【题型7 三角形内角和与三角板的综合运用】
【例7】(23-24八年级·江西南昌·期末)将一副三角板的直角顶点重合按如图放置,,,小明得到下列结论:
①如果,则;
②;
③如果,则;
④如果,则.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】根据平行线的性质和判定和三角形内角和定理逐个判断即可.
【详解】解:∵∠2=30°,∠CAB=90°,
∴∠1=60°,
∵∠E=60°,
∴∠1=∠E,
∴,故①正确;
∵∠CAB=∠DAE=90°,
∴∠BAE+∠CAD=90°﹣∠1+90°+∠1=180°,故②正确;
∵,∠B=45°,
∴∠3=∠B=45°,
∵∠2+∠3=∠DAE=90°,
∴∠2=45°,故③错误;
∵∠CAD=150°,∠BAE+∠CAD=180°,
∴∠BAE=30°,
∵∠E=60°,
∴∠BOE=∠BAE+∠E=90°,
∴∠4+∠B=90°,
∵∠B=45°,
∴∠4=45°,
∵∠C=45°,
∴∠4=∠C,故④正确;
所以其中正确的结论有①②④共3个,
故选:C.
【点睛】本题考查了三角形的内角和定理和平行线的性质和判定,能灵活运用定理进行推理是解此题的关键.
【变式7-1】(23-24八年级·安徽六安·期末)生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,将一副学生用三角板按如图所示的方式放置.若,则的度数是 .
【答案】
【分析】首先根据三角形内角和为180°,求得∠C的度数,又由AE∥BC,即可求得∠CAE的值,根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得∠AFD的度数.
【详解】解:,
,
,
故答案为
【点睛】本题考查三角形内角和定理,熟练掌握计算法则是解题关键.
【变式7-2】(23-24八年级·河北唐山·期末)如图,将一副三角板的直角顶点重合,且使,则的度数是( )
A. B. C. D.
【答案】A
【分析】根据平行线的性质,有同位角相等,即 ,进而求出 ,根据三角形内角和定理即可求出.
【详解】如图:
故答案选A
【点睛】本题考查平行线的性质、两角互补与三角形内角和定理,找到为关键.
【变式7-3】(23-24八年级·湖北随州·期末)将一副学生用的三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)如图叠放,则下列4个结论中正确的个数有( )
①∠AOC+∠BOD=90°;②∠AOC=∠BOD;③∠AOC-∠CEA=15°;④如果OB平分∠DOC,则OC平分∠AOB
A.0 B.1 C.2 D.3
【答案】D
【分析】根据同角的余角相等可得∠AOC=∠BOD;根据三角形的内角和即可得出∠AOC-∠CEA=15°;根据角平分线的定义可判定OC平分∠AOB.
【详解】解:∵∠DOC=∠AOB=90°,
∴∠DOC-∠BOC=∠AOB-∠COB,
即∠BOD=∠AOC,故②正确;
如图,AB与OC交于点P,
∵∠CPE=∠APO,∠C=45°,∠A=30°,∠CEA+∠CPE+∠C=∠AOC+∠APO+∠A=180°,
∴∠AOC-∠CEA=15°.故③正确;
如果OB平分∠DOC,则∠DOB=∠BOC=45°,
则∠AOC=∠BOC=45°,
故OC平分∠AOB,故④正确;
由②知:∠AOC=∠BOD,故当∠AOC=∠BOD=45°时,∠AOC+∠BOD=90°成立,否则不成立,
故①不正确;
综上,②③④正确,共3个,
故选:D.
【点睛】本题考查了余角以及三角形内角和定理,角平分线的定义,熟知余角的性质以及三角形内角和是180°是解答此题的关键.
【题型8 由三角形内角和定理探究角度之间的关系】
【例8】(23-24八年级·全国·单元测试)如图1,已知线段相交于点,连接,则我们把形如这样的图形称为“8字型”.
(1)求证:;
(2)如图2,若和的平分线、相交于点,且与分别相交于点.
①以线段为边的“8字型”有__________个,以点为交点的“8字型”有__________个;
②若,求的度数;
③若角平分线中角的关系改为,试探究与之间存在的数量关系,并证明理由.
【答案】(1)见解析
(2)①3;4;②③
【分析】(1)根据三角形内角和定理得出,,又因为和是对顶角,进而得出结论;
(2)①根据题目给的8字型定义,在图2中查图形的数量即可得出答案;
②根据角平分线的定义得到,再根据三角形内角和定理得出和,两式相加,最后得出,然后把代入计算即可得到答案;
③根据,得到,,再根据三角形内角和定理得出和,两式分别相减得到和,即可得到答案
【详解】(1)证明:∵,,,
∴;
(2)解:①以线段为边的“8字型”有:以和共点M组成的图形;以和共点O组成的图形;以和共点O组成的图形;共有3个;
以点为交点的“8字型”有:以和共点O组成的图形;以和共点O组成的图形;以和共点O组成的图形;以和共点O组成的图形;共有4个;
故答案为:3;4;
②以点为交点的“8字型”中,有,
以点为交点的“8字型”中,有,
,
∵、分别平分和,
,
,
,
;
③
,,
,,
以点为交点的“8字型”中,有,
以点为交点的“8字型”中,有,
,
,
;
【点睛】本题考查了三角形内角和定理:三角形内角和是180度,也考查了角平分线的定义,灵活运用所学知识是关键.
【变式8-1】(23-24八年级·江苏南京·期末)如图,中,,点、分别在边、上,,则下面关于与的关系中一定正确的是( )
A. B.
C. D.
【答案】B
【分析】先求出,再根据三角形内角和定理可得,,从而可得,即可求解.
【详解】解:,
,
,,
,,
,
故选:B.
【点睛】本题考查三角形内角和定理,解题的关键是正确利用和的内角关系.
【变式8-2】(23-24八年级·江西南昌·期中)已知如图,在中,,分别是的高和角平分线,若,
(1)求的度数.
(2)求与,的关系,并说明理由.
【答案】(1)
(2)
【分析】(1)先利用三角形的内角和求得,再利用角平分线的定义和直角三角形的两锐角互余求得,,进而求解即可;
(2)利用三角形的内角和定理、角平分线的定义和直角三角形的两锐角互余求得,,进而求解即可.
【详解】(1)解:∵在中,,,
∴,
∵,分别是的高和角平分线,
∴,,
∴;
(2)解:∵,分别是的高和角平分线,
∴,,
∴
.
【点睛】本题考查三角形的内角和定理、三角形的角平分线和高的定义,熟练掌握三角形的内角和定理和角平分线的定义是解答的关键.
【变式8-3】(23-24八年级·江苏连云港·期末)如图1,过直线外一点作,连接,,的平分线与交于点,点是线段上一动点(不与重合),连接.
(1)若,则_____________°,________________°;
(2)若,求证:;
(3)如图2,的平分线与交于点,连接,若,,试求之间的等量关系.
【答案】(1)25,40;
(2)见解析
(3)或
【分析】(1)根据平行线的性质和角平分线的定义即可求出,根据三角形的内角和定理即可求出;
(2)由平分得到,从而,再根据等角的余角相等即可得证;
(3)分两种情况讨论求解:①点在线段的左侧,②点在线段的右侧.
【详解】(1)解:∵,
∴,
∵平分,
∴,
∵,
∴;
故答案为:25,40
(2)证明:∵平分,
∴,
∵,
∴,
∵
∴
∵
∴;
(3)解:①当点在线段的左侧时,如图,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵平分,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴;
②当点在线段的右侧时,如图,
∵,
∴,
∵,
∴,
∵,
∴,
∴.
∵平分,
∴,
∵,
∴,
∵
∴,
∵,
∴
∵,
∴
∴;
综上,之间的等量关系为:或
【点睛】本题考查平行线的性质,角平分线的定义,角的和差,三角形的内角和定理,综合运用相关知识,掌握分类讨论思想是解题的关键.
知识点2:直角三角形的性质与判定
(1)直角三角形的两个锐角互余.
(2)有两个角互余的三角形是直角三角形.
【提示】直角三角形的性质和判定的应用思路:
(1)见直角三角形,可得两锐角互余.
(2)见两角互余,可得直角三角形.
【题型9 由直角三角形的性质求角度】
【例9】(23-24八年级·河南郑州·期中)在直角三角形中,比的3倍还多,则的大小为 .
【答案】或
【分析】本题主要考查了直角三角形两锐角互余,解题的关键是注意进行分类讨论,分两种情况:当为直角时,当为直角时,分别求出结果即可.
【详解】解:当为直角时,,
当为直角时,,
∵比的3倍还多,
∴,
∴,
∴,
∴,
故答案为:或.
【变式9-1】(23-24八年级·河南南阳·期末)一副三角板按如图所示放置,点在上,点在上,若,则 .
【答案】/110度
【分析】本题考查了直角三角形两锐角互余,对顶角的性质,余角性质,邻补角的性质,由直角三角形两锐角互余可得,,进而由余角性质可得,即可得到,再利用邻补角的性质即可求解,正确识图是解题的关键.
【详解】解:如图,∵,
∴,,
∵,
∴,
∵,
∴,
∴,
故答案为:.
【变式9-2】(23-24八年级·湖南株洲·期中)如图,在中,,,于D,于E,与交于H,则 .
【答案】
【分析】本题考查直角三角形两个锐角互余,三角形的高的性质等知识,延长交于点M,可得在中,三边所在的高交于一点,即,由此即可解答.
【详解】解:延长交于点M,如图,
在中,三边所在的高交于一点,
∴,
∵,
∴,
故答案为:.
【变式9-3】(23-24八年级·四川成都·期末)如图,有一副三角板ABC与DEF,其中∠C=∠F=90°,∠A=60°,∠D=45°,在一平面内将这副三角板进行拼摆,使得点B、E重合,且点B、C、F三点在同一直线上,则∠ABD的度数是 °.
【答案】15°或105°或75°或165
【分析】根据题意画出四种情况,先根据直角三角形的两锐角互余求出∠ABC和∠DEF的度数,再分别求出∠ABD即可.
【详解】解:有四种情况:
第一种情况:如图1,
∵∠C=∠F=90°,∠A=60°,∠D=45°,
∴∠ABC=90°-∠A=30°,∠DBF=90°-∠D=45°,
∴∠ABD=∠DBF-∠ABC=45°-30°=15°;
第二种情况:如图2,
∵∠ABC=30°,∠DEF=45°,
∴∠ABD=1800°-∠ABC-∠DEF=180°-30°-45°=105°;
第三种情况:如图3,
∵∠ABC=30°,∠DEF=45°,
∴∠ABD=∠ABC+∠DEF=30°+45°=75°;
第四种情况:如图4,
∵∠DEF=45°,
∴∠DBC=180°-∠DEF=135°,
∵∠ABC=30°,
∴∠ABD=∠ABC+∠DBC=30°+135°=165°;
∠ABD的度数是15°或105°或75°或165°,
故答案为:15°或105°或75°或165.
【点睛】本题考查了直角三角形的性质和三角形内角和定理,能正确画出符合的所有图形是解此题的关键.
【题型10 锐角互余的三角形是直角三角形】
【例10】(23-24八年级·全国·课堂例题)如图,在中,是边上的高,E是边上一点,交于点M,且.求证:是直角三角形.
【答案】见解析
【分析】本题考查了直角三角形的性质与判定;由是边上的高,得;再由,即可得结论成立.
【详解】解:∵是边上的高,
∴,
∴.
∵,
∴,
∴是直角三角形.
【变式10-1】(23-24八年级·江苏南京·期中)证明:有两个角互余的三角形是直角三角形.
已知:如图, ,
求证: .
证明:
【答案】见解析
【分析】本题考查了直角三角形的性质,三角形内角和定理,熟练运用三角形内角和定理是本题的关键.利用三角形的内角和定理求解即可.
【详解】已知:在中,,
求证:是直角三角形,
证明:在中,(三角形三个内角的和等于).
(等式性质).
(已知),
(等量代换),
是直角三角形.
【变式10-2】(23-24八年级·河南周口·阶段练习)在下列条件中:①,②,③,④中,能确定是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】本题考查了三角形内角和定理,以及三角形的形状判定,根据直角三角形的判定方法对各个选项进行分析,从而得到答案.
【详解】解:①因为,则,所以是直角三角形;
②因为,设,则,,,所以是直角三角形;
③因为,所以,则,所以是直角三角形;
④因为,所以,又,,解得,是直角三角形;
能确定是直角三角形的有①②③④共4个,
故选:D.
【变式10-3】(23-24八年级·全国·课后作业)如图,平分,平分,和交于点E.写出图中所有的直角三角形(不要求证明).
【答案】,,
【分析】根据平行线的性质和角平分线的定义,结合三角形的内角和定理证得即可得出结论.
【详解】解:∵,
∴,
∵平分,平分,
∴,,
∴,
∴是直角三角形,
∴,
∵和交于点E,
∴,
∴,,均为直角三角形.
【点睛】本题考查直角三角形的判定,涉及平行线的性质、角平分线的定义、邻补角、锐角互余的三角形是直角三角形等知识,熟练掌握锐角互余的三角形是直角三角形是解答的关键.
21世纪教育网(www.21cnjy.com)
【人教版】
【题型1 证明三角形内角和】 1
【题型2 由三角形内角和直接求角度】 3
【题型3 由三角形内角和判断三角形形状】 4
【题型4 三角形内角和与平行线的综合运用】 4
【题型5 三角形内角和与翻折的综合运用】 5
【题型6 三角形内角和与角平分线的综合运用】 7
【题型7 三角形内角和与三角板的综合运用】 8
【题型8 由三角形内角和定理探究角度之间的关系】 9
【题型9 由直角三角形的性质求角度】 11
【题型10 锐角互余的三角形是直角三角形】 12
知识点1:三角形的内角和定理
(1)三角形内角和定理:三角形三个内角的和等于.
(2)因为三角形三个内角的和等于,所以任何一个三角形中至少有两个锐角,最多有一个钝角或直角.
【提示】(1)三角形内角和定理适用于任意三角形.
(2)任何一个三角形中,至少有两个锐角,最多有一个钝角或直角.
【题型1 证明三角形内角和】
【例1】(23-24八年级·河北邢台·阶段练习)在探究证明“三角形的内角和是”时,综合实践小组的同学作了如下四种辅助线,其中能证明“三角形的内角和是”的有( )
①如图1,过点C作;
②如图2,过上一点D分别作,;
③如图3,延长到点F,过点C作;
④如图4,过点C作于点D.
A.①②③ B.①②④ C.②③④ D.①③④
【变式1-1】(23-24八年级·全国·课堂例题)如图,折叠一张三角形纸片,把三角形三个角拼在一起,就能验证一个几何定理.请写出这个定理的名称: .
【变式1-2】(23-24八年级·河北石家庄·阶段练习)下面是一道习题,需要填写符号处的内容,下列填写正确的是( )
已知:.求证:. 证明:如图,过点C作. ∵(已知), ∴★,■(①). ∵(②), ∴(等量代换).
A.★处填2 B.■处填1
C.①内错角相等,两直线平行 D.②平角定义
【变式1-3】(23-24·重庆忠县·八年级统考期末)三角形的内角和定理是初中数学学习中的一个重要定理,下面给出了该定理的一种证明方法.
已知:如图, . 求证:. 证明:作的延长线,在外部,以为一边,作. 所以,(内错角相等,两直线平行). 所以,( ). 因为,,,组成一个平角, 所以,(平角的定义), 所以,( ).
(1)请将上面的“已知”和推理“依据”补充完整;
(2)该定理有多种证明方法,请再写出一种证明方法.
【题型2 由三角形内角和直接求角度】
【例2】(23-24八年级·江苏宿迁·期末)如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.若为倍角三角形,,则 .
【变式2-1】(23-24八年级·新疆巴音郭楞·期末)如图1是某款婴儿手推车,如图2是其侧面的示意图,若,,,则的度数为 .
【变式2-2】(23-24八年级·福建宁德·期末)将沿方向平移得到.若,,则的度数是( )
A. B. C. D.
【变式2-3】(23-24八年级·江苏宿迁·期末)已知:如图,在四边形中,点在上,与互余,且,试猜想与的位置关系,并说明理由.
【题型3 由三角形内角和判断三角形形状】
【例3】(23-24八年级·河北廊坊·期中)如图,当时,该三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
【变式3-1】(23-24八年级·广西梧州·期中)中,若,则的形状是( )
A.锐角三角形 B.直角三角形 C.钝角二角形 D.无法确定
【变式3-2】(23-24八年级·安徽淮北·阶段练习)如果一个三角形的两个内角都小于30°,那么这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
【变式3-3】(23-24八年级·重庆秀山·期中)中,,请判断三角形的形状并证明.
【题型4 三角形内角和与平行线的综合运用】
【例4】(23-24八年级·河南平顶山·期末)如图,△CEF中,∠E=70°,∠F=50°,且AB∥CF ,AD∥CE,连接BC,CD,则∠A的度数是( )
A.40° B.45° C.50° D.60°
【变式4-1】(23-24八年级·四川成都·期末)如图,ABCD,AC与BD相交于点O,若∠A=25°,∠D=45°,则∠AOB的大小为( )
A.90° B.110° C.120° D.135°
【变式4-2】(23-24八年级·陕西渭南·期中)如图,在三角形中,点D,H,E分别是边,,上的点,连接,,F为上一点,连接,若,,.则的度数为 .
【变式4-3】(23-24八年级·湖北孝感·期中)如图,直线,点A,B分别是,上的动点,点G在上,,和的角平分线交于点D,若,则m的值为 .
【题型5 三角形内角和与翻折的综合运用】
【例5】(23-24八年级·江苏扬州·期末)如图,、是边、上的点,沿翻折后得到,沿翻折后得到,且点在边上,沿翻折后得到,且点在边上,若,则( )
A. B. C. D.
【变式5-1】(23-24八年级·江苏连云港·期中)如图,将直角三角形纸片沿(D是斜边上一点)折叠,使点B落在点处,若,则的度数是 °.(用含的代数式表示)
【变式5-2】(23-24八年级·广西南宁·期中)如图,在折纸活动中,小李制作了一张的纸片,点,分别在边,上,将沿着折叠压平,与重合,若,则 .
【变式5-3】(23-24八年级·福建漳州·期中)如图,在中,,,D是线段上一个动点,连接,把沿折叠,点C落在同一平面内的点E处,当平行于的边时,的度数为 .
【题型6 三角形内角和与角平分线的综合运用】
【例6】(23-24八年级·江苏淮安·期末)如图,中,,,平分,于D,,则的度数 .
【变式6-1】(23-24八年级·江苏徐州·期中)如图,、是的角平分线,与交于点,, (用含的代数式表示).
【变式6-2】(23-24八年级·辽宁营口·期中)如图,中,是边上的高,分别是、的平分线, ,,则( ).
A. B. C. D.
【变式6-3】(23-24八年级·江苏苏州·期中)新定义:在中,若存在一个内角是另外一个内角度数的n倍(n为大于1的正整数),则称为n倍角三角形.例如,,可知,所以为2倍角三角形.
(1)在中,,则为 倍角三角形.
(2)如图1,直线与直线相交于O,;已知、的角平分线交于点C,在中,在中,如果有一个角是另一个角的2倍,请求出的度数.
(3)如图2,直线⊥直线于点O,点A、点B分别在射线上,已知、的角平分线分别与的角平分线所在的直线交于点、.若为3倍角三角形,试求的度数.
【题型7 三角形内角和与三角板的综合运用】
【例7】(23-24八年级·江西南昌·期末)将一副三角板的直角顶点重合按如图放置,,,小明得到下列结论:
①如果,则;
②;
③如果,则;
④如果,则.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【变式7-1】(23-24八年级·安徽六安·期末)生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,将一副学生用三角板按如图所示的方式放置.若,则的度数是 .
【变式7-2】(23-24八年级·河北唐山·期末)如图,将一副三角板的直角顶点重合,且使,则的度数是( )
A. B. C. D.
【变式7-3】(23-24八年级·湖北随州·期末)将一副学生用的三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)如图叠放,则下列4个结论中正确的个数有( )
①∠AOC+∠BOD=90°;②∠AOC=∠BOD;③∠AOC-∠CEA=15°;④如果OB平分∠DOC,则OC平分∠AOB
A.0 B.1 C.2 D.3
【题型8 由三角形内角和定理探究角度之间的关系】
【例8】(23-24八年级·全国·单元测试)如图1,已知线段相交于点,连接,则我们把形如这样的图形称为“8字型”.
(1)求证:;
(2)如图2,若和的平分线、相交于点,且与分别相交于点.
①以线段为边的“8字型”有__________个,以点为交点的“8字型”有__________个;
②若,求的度数;
③若角平分线中角的关系改为,试探究与之间存在的数量关系,并证明理由.
【变式8-1】(23-24八年级·江苏南京·期末)如图,中,,点、分别在边、上,,则下面关于与的关系中一定正确的是( )
A. B.
C. D.
【变式8-2】(23-24八年级·江西南昌·期中)已知如图,在中,,分别是的高和角平分线,若,
(1)求的度数.
(2)求与,的关系,并说明理由.
【变式8-3】(23-24八年级·江苏连云港·期末)如图1,过直线外一点作,连接,,的平分线与交于点,点是线段上一动点(不与重合),连接.
(1)若,则_____________°,________________°;
(2)若,求证:;
(3)如图2,的平分线与交于点,连接,若,,试求之间的等量关系.
知识点2:直角三角形的性质与判定
(1)直角三角形的两个锐角互余.
(2)有两个角互余的三角形是直角三角形.
【提示】直角三角形的性质和判定的应用思路:
(1)见直角三角形,可得两锐角互余.
(2)见两角互余,可得直角三角形.
【题型9 由直角三角形的性质求角度】
【例9】(23-24八年级·河南郑州·期中)在直角三角形中,比的3倍还多,则的大小为 .
【变式9-1】(23-24八年级·河南南阳·期末)一副三角板按如图所示放置,点在上,点在上,若,则 .
【变式9-2】(23-24八年级·湖南株洲·期中)如图,在中,,,于D,于E,与交于H,则 .
【变式9-3】(23-24八年级·四川成都·期末)如图,有一副三角板ABC与DEF,其中∠C=∠F=90°,∠A=60°,∠D=45°,在一平面内将这副三角板进行拼摆,使得点B、E重合,且点B、C、F三点在同一直线上,则∠ABD的度数是 °.
【题型10 锐角互余的三角形是直角三角形】
【例10】(23-24八年级·全国·课堂例题)如图,在中,是边上的高,E是边上一点,交于点M,且.求证:是直角三角形.
【变式10-1】(23-24八年级·江苏南京·期中)证明:有两个角互余的三角形是直角三角形.
已知:如图, ,
求证: .
证明:
【变式10-2】(23-24八年级·河南周口·阶段练习)在下列条件中:①,②,③,④中,能确定是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
【变式10-3】(23-24八年级·全国·课后作业)如图,平分,平分,和交于点E.写出图中所有的直角三角形(不要求证明).
21世纪教育网(www.21cnjy.com)
专题11.3 三角形的内角和定理【十大题型】
【人教版】
【题型1 证明三角形内角和】 1
【题型2 由三角形内角和直接求角度】 6
【题型3 由三角形内角和判断三角形形状】 8
【题型4 三角形内角和与平行线的综合运用】 10
【题型5 三角形内角和与翻折的综合运用】 13
【题型6 三角形内角和与角平分线的综合运用】 18
【题型7 三角形内角和与三角板的综合运用】 22
【题型8 由三角形内角和定理探究角度之间的关系】 26
【题型9 由直角三角形的性质求角度】 33
【题型10 锐角互余的三角形是直角三角形】 37
知识点1:三角形的内角和定理
(1)三角形内角和定理:三角形三个内角的和等于.
(2)因为三角形三个内角的和等于,所以任何一个三角形中至少有两个锐角,最多有一个钝角或直角.
【提示】(1)三角形内角和定理适用于任意三角形.
(2)任何一个三角形中,至少有两个锐角,最多有一个钝角或直角.
【题型1 证明三角形内角和】
【例1】(23-24八年级·河北邢台·阶段练习)在探究证明“三角形的内角和是”时,综合实践小组的同学作了如下四种辅助线,其中能证明“三角形的内角和是”的有( )
①如图1,过点C作;
②如图2,过上一点D分别作,;
③如图3,延长到点F,过点C作;
④如图4,过点C作于点D.
A.①②③ B.①②④ C.②③④ D.①③④
【答案】A
【分析】本题主要考查三角形内角和的定理的证明,平行线的性质,熟练掌握转化的思想以及平角的定义是解决本题的关键.运用转化的思想作出相应的平行线,把三角形的内角进行转化,再根据平角的定义逐一判断即可得答案.
【详解】①∵,
∴,
∵,
∴,故①符合题意,
②∵,,
∴,,
∴,
∵,
∴,故②符合题意,
③∵,
∴,
∵,
∴,故③符合题意,
④ ,
,
不能证明“三角形的内角和等于”故④不符合题意,
故选:A.
【变式1-1】(23-24八年级·全国·课堂例题)如图,折叠一张三角形纸片,把三角形三个角拼在一起,就能验证一个几何定理.请写出这个定理的名称: .
【答案】三角形内角和定理
【分析】根据折叠前后的两个角相等,把三角形的三个角转化为一个平角,可以得到三角形内角和定理.
【详解】解:根据折叠的性质,,
∵,
∴,
∴定理为:三角形内角和定理.
故答案为:三角形内角和定理.
【点睛】本题主要考查了三角形的内角和定理的证明,熟练掌握翻折变换的性质是解题的关键.
【变式1-2】(23-24八年级·河北石家庄·阶段练习)下面是一道习题,需要填写符号处的内容,下列填写正确的是( )
已知:.求证:. 证明:如图,过点C作. ∵(已知), ∴★,■(①). ∵(②), ∴(等量代换).
A.★处填2 B.■处填1
C.①内错角相等,两直线平行 D.②平角定义
【答案】D
【分析】根据题意结合平行线的性质进行证明判断即可.
【详解】证明:如图,过点C作.
∵(已知),
∴1,2(两直线平行,内错角相等).
∵(平角定义),
∴(等量代换).
故选D
【点睛】本题主要考查了三角形内角和定理的证明,平行线的性质,正确理解题意是解题的关键.
【变式1-3】(23-24·重庆忠县·八年级统考期末)三角形的内角和定理是初中数学学习中的一个重要定理,下面给出了该定理的一种证明方法.
已知:如图, . 求证:. 证明:作的延长线,在外部,以为一边,作. 所以,(内错角相等,两直线平行). 所以,( ). 因为,,,组成一个平角, 所以,(平角的定义), 所以,( ).
(1)请将上面的“已知”和推理“依据”补充完整;
(2)该定理有多种证明方法,请再写出一种证明方法.
【答案】(1)、、是的三个内角;两直线平行,同位角相等;等量代换
(2)见解析
【分析】本题考查了三角形内角和定理,平行线的判定与性质:
(1)在外部,以为一边,作.根据平行线的判定与性质及平角定义求解即可;
(2)过点A作,根据平行线的性质°,由此证明即可.
【详解】(1)解:已知:如图,、、是的三个内角.
求证:.
证明:如图,作的延长线,在外部,以为一边,作.
所以,(内错角相等,两直线平行).
所以,(两直线平行,同位角相等).
因为,组成一个平角,
所以,(平角的定义),
所以,(等量代换).
(2)证明:如图,过点A作,
∵,
∴(两直线平行,内错角相等).
(两直线平行,同旁内角互补).
即.
∴.
【题型2 由三角形内角和直接求角度】
【例2】(23-24八年级·江苏宿迁·期末)如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.若为倍角三角形,,则 .
【答案】或或或
【分析】该题主要考查了三角形内角和定理,解题的关键是分类讨论.
根据“倍角三角形”定义分为当时,当时,当时,当时,结合三角形内角和定理求解即可;
【详解】解:当时,;
当时,,;
当时,,解得:;
当时,,解得:;
故答案为:或或或.
【变式2-1】(23-24八年级·新疆巴音郭楞·期末)如图1是某款婴儿手推车,如图2是其侧面的示意图,若,,,则的度数为 .
【答案】/85度
【分析】本题考查平行线的性质和三角形内角和定理,根据平行线的性质可得,利用三角形内角和定理得出的度数,即可求解.
【详解】解:如图,
∵,
∴,
∵
∴,
∴
∴,
故答案为:.
【变式2-2】(23-24八年级·福建宁德·期末)将沿方向平移得到.若,,则的度数是( )
A. B. C. D.
【答案】B
【分析】本题考查了平移的性质,掌握平移的性质是解题的关键.根据图形平移,图形的大小不变,对应角、对应边相等即可求解.
【详解】解:根据题意,由平移的性质得:,
∴,
故选:B .
【变式2-3】(23-24八年级·江苏宿迁·期末)已知:如图,在四边形中,点在上,与互余,且,试猜想与的位置关系,并说明理由.
【答案】,理由见解析
【分析】本题考查了垂线的定义,余角的定义,三角形内角和定理,根据,推出,进而得到,由,得到,从而得到,推出.
【详解】解:,理由见如下:
,
,
,
,
,
,
.
【题型3 由三角形内角和判断三角形形状】
【例3】(23-24八年级·河北廊坊·期中)如图,当时,该三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
【答案】B
【分析】本题考查了三角形内角和定理,三角形的分类.利用三角形内角和定理得到,结合已知计算即可求解.
【详解】解:如图,且,
∴,
∴,
∴,
∴该三角形的形状是直角三角形,
故选:B.
【变式3-1】(23-24八年级·广西梧州·期中)中,若,则的形状是( )
A.锐角三角形 B.直角三角形 C.钝角二角形 D.无法确定
【答案】B
【分析】本题主要考查三角形内角和定理,根据在中,,可求出的度数,即可得出结论,熟知三角形内角和是是解答本题的关键.
【详解】解:∵在中,,
∴,
∵,
∴,
∴,
∴是直角三角形.
故选:B.
【变式3-2】(23-24八年级·安徽淮北·阶段练习)如果一个三角形的两个内角都小于30°,那么这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
【答案】C
【分析】根据三角形的内角和定理即可得到结论.
【详解】解:∵三角形的两个内角都小于30°,
∴这两个内角的和小于60°,
∵三个内角的和为180°,
∴另一个角大于120°,
∴这个三角形是钝角三角形,
故选:C.
【点睛】本题考查了三角形的内角和定理,熟练掌握三角形的内角和定理是解题的关键.
【变式3-3】(23-24八年级·重庆秀山·期中)中,,请判断三角形的形状并证明.
【答案】是直角三角形,证明见解析
【分析】本题主要考查了三角形内角和定理,设,根据三角形内角和为180度建立方程,解方程求出x的值,进而求出,由此可得结论.
【详解】解;是直角三角形,证明如下;
∵,
∴可设,
∵,
∴,
解得,
∴,
∴是直角三角形.
【题型4 三角形内角和与平行线的综合运用】
【例4】(23-24八年级·河南平顶山·期末)如图,△CEF中,∠E=70°,∠F=50°,且AB∥CF ,AD∥CE,连接BC,CD,则∠A的度数是( )
A.40° B.45° C.50° D.60°
【答案】D
【分析】连接AC并延长交EF于点M.由平行线的性质得,,再由等量代换得,先求出即可求出.
【详解】连接AC并延长交EF于点M.
∵,
∴,
∵,
∴,
∴,
∵,
∴,
故选D.
【点睛】本题主要考查了平行线的性质以及三角形的内角和定理,属于基础题型.
【变式4-1】(23-24八年级·四川成都·期末)如图,ABCD,AC与BD相交于点O,若∠A=25°,∠D=45°,则∠AOB的大小为( )
A.90° B.110° C.120° D.135°
【答案】B
【分析】首先根据两直线平行,内错角相等得出∠B=∠D=45°,然后由△AOB的内角和为180°,求出∠AOB的大小.
【详解】解:∵ABCD,
∴∠B=∠D=45°.
∵∠A+∠AOB+∠B=180°,
∴∠AOB=180°﹣25°﹣45°=110°.
故选:B.
【点睛】本题考查了平行线的性质及三角形的内角和定理,根据平行线的性质得出∠B=∠D=45°是解题的关键,属于基础题型,比较简单.
【变式4-2】(23-24八年级·陕西渭南·期中)如图,在三角形中,点D,H,E分别是边,,上的点,连接,,F为上一点,连接,若,,.则的度数为 .
【答案】
【分析】由,,得到,根据平行线的判定,得到,根据平行线的性质,得到,根据三角形内角和定理,求出的度数,即可求解,
本题考查了,平行线的性质与判定,三角形内角和定理,解题的关键是:熟练掌握相关性质定理.
【详解】解:∵,,
∴,
∴,
∴,
∵,
∴,
故答案为:.
【变式4-3】(23-24八年级·湖北孝感·期中)如图,直线,点A,B分别是,上的动点,点G在上,,和的角平分线交于点D,若,则m的值为 .
【答案】76
【分析】先由平行线的性质得到,再根据三角形内角和定理和角平分线的定义求出m的值.
【详解】解:过点C作,
,
,,
,
,
,
,
由题意可得为的角平分线,为的角平分线,
,,
,,
,
,
,
.
故答案为:76.
【点睛】本题考查了平行线的性质和三角形内角和定理,熟练掌握平行线的性质和三角形内角和定理是解题的关键.
【题型5 三角形内角和与翻折的综合运用】
【例5】(23-24八年级·江苏扬州·期末)如图,、是边、上的点,沿翻折后得到,沿翻折后得到,且点在边上,沿翻折后得到,且点在边上,若,则( )
A. B. C. D.
【答案】D
【分析】本题考查了折叠的性质,三角形的内角和定理.根据折叠的性质以及三角形内角和定理得出,,将已知数据代入,即可求解.
【详解】解:如图所示,
依题意,,
∴
,
即,
,,
∵,
∴,
∴,
∴,
∴,
故选:D.
【变式5-1】(23-24八年级·江苏连云港·期中)如图,将直角三角形纸片沿(D是斜边上一点)折叠,使点B落在点处,若,则的度数是 °.(用含的代数式表示)
【答案】
【分析】本题考查了三角形折叠中的角度问题,根据角度间关系可得,再根据折叠性质得到,最后推出,即可得出答案,理清角度间的数量关系是解题关键.
【详解】解:,
,
将直角三角形纸片沿(D是斜边上一点)折叠,使点B落在点处,
,
,
,
,
.
故答案为:.
【变式5-2】(23-24八年级·广西南宁·期中)如图,在折纸活动中,小李制作了一张的纸片,点,分别在边,上,将沿着折叠压平,与重合,若,则 .
【答案】/65度
【分析】本题考查折叠的性质,三角形内角和定理.由折叠可得,,进而可得,结合,可得,即可求解.
【详解】解:将沿着折叠压平,与重合,
,,
,
,
,
,
,
,
故答案为:.
【变式5-3】(23-24八年级·福建漳州·期中)如图,在中,,,D是线段上一个动点,连接,把沿折叠,点C落在同一平面内的点E处,当平行于的边时,的度数为 .
【答案】或
【分析】本题考查了平行线的性质,折叠问题,三角形的内角和等知识点,分两种情况,和,分别画出图形,再利用平行线的性质求解即可,正确分类并画出图形是解题的关键.
【详解】由折叠的性质得:,
设,
∵,
∴,
由题意,分以下两种情况:
如图,当时,
∵,
∴,
∵,
∴,
解得,
即;
如图,当时,
∴,
∵,
∴,
解得,
即,
综上,的大小为或.
故答案为:或.
【题型6 三角形内角和与角平分线的综合运用】
【例6】(23-24八年级·江苏淮安·期末)如图,中,,,平分,于D,,则的度数 .
【答案】
【分析】本题考查了三角形的内角和以及角平分线的定义,熟练掌握三角形的内角和以及角平分线的定义是解题的关键.首先根据三角形的内角和定理求得的度数,根据角平分线的定义求得的度数,则可以求解,然后在中,利用内角和定理即可求得的度数.
【详解】,,
,
平分,
,
,
,
,
,
,
,
.
故答案为:.
【变式6-1】(23-24八年级·江苏徐州·期中)如图,、是的角平分线,与交于点,, (用含的代数式表示).
【答案】
【分析】此题考查了与角平分线有关的三角形内角和定理,先求出,再利用角平分线求出,再利用三角形内角和定理即可求出答案.
【详解】解:∵,
∴,
∵、是的角平分线,
∴,
∴,
∵,
∴,
故答案为:
【变式6-2】(23-24八年级·辽宁营口·期中)如图,中,是边上的高,分别是、的平分线, ,,则( ).
A. B. C. D.
【答案】A
【分析】此题考查了三角形内角和定理及角平分线的性质,依据是边上的高,,即可得到,依据 ,平分,即可得到,再依据是的平分线,得到,可得,熟练掌握三角形内角和定理以及角平分线定义的运用是解题的关键.
【详解】解:∵是边上的高,
∴,
∵,
∴,
∵,平分,
∴,
∴,
∵是的平分线,
∴,
∴
故选:.
【变式6-3】(23-24八年级·江苏苏州·期中)新定义:在中,若存在一个内角是另外一个内角度数的n倍(n为大于1的正整数),则称为n倍角三角形.例如,,可知,所以为2倍角三角形.
(1)在中,,则为 倍角三角形.
(2)如图1,直线与直线相交于O,;已知、的角平分线交于点C,在中,在中,如果有一个角是另一个角的2倍,请求出的度数.
(3)如图2,直线⊥直线于点O,点A、点B分别在射线上,已知、的角平分线分别与的角平分线所在的直线交于点、.若为3倍角三角形,试求的度数.
【答案】(1)3
(2)或或或
(3)或
【分析】本题考查三角形的内角和定理,余角的意义等知识,读懂新定义倍角三角形的意义和分类讨论是解决问题的基础和关键.
(1)由,可知,再根据倍角三角形的定义可得结论.
(2)先求出,,然后分四种情形分别求解即可.
(3)先证明,,然后分四种情形分别求解即可.
【详解】(1),,
,
,
为3倍角三角形,
故答案为:3;
(2)解:∵,
∴.
又∵平分,平分,
∴,
∴.
①当时,
∵,
∴;
②当时,
∵,
∴;
③当时,
∵,
∴;
④当时,
∵,
∴,
∴.
综上,在中当一个角是另一个角的2倍时,等于或或或;
(3)平分,平分,
,,
,
;
又平分,
①,
②;
得:.
若为3倍角三角形:
若,
,
,
;
若,
,
(不符合题意,舍去);
若,
,
;
若,
,,
(不符合题意,舍去);
综上所述,等于或时,为3倍角三角形.
【题型7 三角形内角和与三角板的综合运用】
【例7】(23-24八年级·江西南昌·期末)将一副三角板的直角顶点重合按如图放置,,,小明得到下列结论:
①如果,则;
②;
③如果,则;
④如果,则.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】根据平行线的性质和判定和三角形内角和定理逐个判断即可.
【详解】解:∵∠2=30°,∠CAB=90°,
∴∠1=60°,
∵∠E=60°,
∴∠1=∠E,
∴,故①正确;
∵∠CAB=∠DAE=90°,
∴∠BAE+∠CAD=90°﹣∠1+90°+∠1=180°,故②正确;
∵,∠B=45°,
∴∠3=∠B=45°,
∵∠2+∠3=∠DAE=90°,
∴∠2=45°,故③错误;
∵∠CAD=150°,∠BAE+∠CAD=180°,
∴∠BAE=30°,
∵∠E=60°,
∴∠BOE=∠BAE+∠E=90°,
∴∠4+∠B=90°,
∵∠B=45°,
∴∠4=45°,
∵∠C=45°,
∴∠4=∠C,故④正确;
所以其中正确的结论有①②④共3个,
故选:C.
【点睛】本题考查了三角形的内角和定理和平行线的性质和判定,能灵活运用定理进行推理是解此题的关键.
【变式7-1】(23-24八年级·安徽六安·期末)生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,将一副学生用三角板按如图所示的方式放置.若,则的度数是 .
【答案】
【分析】首先根据三角形内角和为180°,求得∠C的度数,又由AE∥BC,即可求得∠CAE的值,根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得∠AFD的度数.
【详解】解:,
,
,
故答案为
【点睛】本题考查三角形内角和定理,熟练掌握计算法则是解题关键.
【变式7-2】(23-24八年级·河北唐山·期末)如图,将一副三角板的直角顶点重合,且使,则的度数是( )
A. B. C. D.
【答案】A
【分析】根据平行线的性质,有同位角相等,即 ,进而求出 ,根据三角形内角和定理即可求出.
【详解】如图:
故答案选A
【点睛】本题考查平行线的性质、两角互补与三角形内角和定理,找到为关键.
【变式7-3】(23-24八年级·湖北随州·期末)将一副学生用的三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)如图叠放,则下列4个结论中正确的个数有( )
①∠AOC+∠BOD=90°;②∠AOC=∠BOD;③∠AOC-∠CEA=15°;④如果OB平分∠DOC,则OC平分∠AOB
A.0 B.1 C.2 D.3
【答案】D
【分析】根据同角的余角相等可得∠AOC=∠BOD;根据三角形的内角和即可得出∠AOC-∠CEA=15°;根据角平分线的定义可判定OC平分∠AOB.
【详解】解:∵∠DOC=∠AOB=90°,
∴∠DOC-∠BOC=∠AOB-∠COB,
即∠BOD=∠AOC,故②正确;
如图,AB与OC交于点P,
∵∠CPE=∠APO,∠C=45°,∠A=30°,∠CEA+∠CPE+∠C=∠AOC+∠APO+∠A=180°,
∴∠AOC-∠CEA=15°.故③正确;
如果OB平分∠DOC,则∠DOB=∠BOC=45°,
则∠AOC=∠BOC=45°,
故OC平分∠AOB,故④正确;
由②知:∠AOC=∠BOD,故当∠AOC=∠BOD=45°时,∠AOC+∠BOD=90°成立,否则不成立,
故①不正确;
综上,②③④正确,共3个,
故选:D.
【点睛】本题考查了余角以及三角形内角和定理,角平分线的定义,熟知余角的性质以及三角形内角和是180°是解答此题的关键.
【题型8 由三角形内角和定理探究角度之间的关系】
【例8】(23-24八年级·全国·单元测试)如图1,已知线段相交于点,连接,则我们把形如这样的图形称为“8字型”.
(1)求证:;
(2)如图2,若和的平分线、相交于点,且与分别相交于点.
①以线段为边的“8字型”有__________个,以点为交点的“8字型”有__________个;
②若,求的度数;
③若角平分线中角的关系改为,试探究与之间存在的数量关系,并证明理由.
【答案】(1)见解析
(2)①3;4;②③
【分析】(1)根据三角形内角和定理得出,,又因为和是对顶角,进而得出结论;
(2)①根据题目给的8字型定义,在图2中查图形的数量即可得出答案;
②根据角平分线的定义得到,再根据三角形内角和定理得出和,两式相加,最后得出,然后把代入计算即可得到答案;
③根据,得到,,再根据三角形内角和定理得出和,两式分别相减得到和,即可得到答案
【详解】(1)证明:∵,,,
∴;
(2)解:①以线段为边的“8字型”有:以和共点M组成的图形;以和共点O组成的图形;以和共点O组成的图形;共有3个;
以点为交点的“8字型”有:以和共点O组成的图形;以和共点O组成的图形;以和共点O组成的图形;以和共点O组成的图形;共有4个;
故答案为:3;4;
②以点为交点的“8字型”中,有,
以点为交点的“8字型”中,有,
,
∵、分别平分和,
,
,
,
;
③
,,
,,
以点为交点的“8字型”中,有,
以点为交点的“8字型”中,有,
,
,
;
【点睛】本题考查了三角形内角和定理:三角形内角和是180度,也考查了角平分线的定义,灵活运用所学知识是关键.
【变式8-1】(23-24八年级·江苏南京·期末)如图,中,,点、分别在边、上,,则下面关于与的关系中一定正确的是( )
A. B.
C. D.
【答案】B
【分析】先求出,再根据三角形内角和定理可得,,从而可得,即可求解.
【详解】解:,
,
,,
,,
,
故选:B.
【点睛】本题考查三角形内角和定理,解题的关键是正确利用和的内角关系.
【变式8-2】(23-24八年级·江西南昌·期中)已知如图,在中,,分别是的高和角平分线,若,
(1)求的度数.
(2)求与,的关系,并说明理由.
【答案】(1)
(2)
【分析】(1)先利用三角形的内角和求得,再利用角平分线的定义和直角三角形的两锐角互余求得,,进而求解即可;
(2)利用三角形的内角和定理、角平分线的定义和直角三角形的两锐角互余求得,,进而求解即可.
【详解】(1)解:∵在中,,,
∴,
∵,分别是的高和角平分线,
∴,,
∴;
(2)解:∵,分别是的高和角平分线,
∴,,
∴
.
【点睛】本题考查三角形的内角和定理、三角形的角平分线和高的定义,熟练掌握三角形的内角和定理和角平分线的定义是解答的关键.
【变式8-3】(23-24八年级·江苏连云港·期末)如图1,过直线外一点作,连接,,的平分线与交于点,点是线段上一动点(不与重合),连接.
(1)若,则_____________°,________________°;
(2)若,求证:;
(3)如图2,的平分线与交于点,连接,若,,试求之间的等量关系.
【答案】(1)25,40;
(2)见解析
(3)或
【分析】(1)根据平行线的性质和角平分线的定义即可求出,根据三角形的内角和定理即可求出;
(2)由平分得到,从而,再根据等角的余角相等即可得证;
(3)分两种情况讨论求解:①点在线段的左侧,②点在线段的右侧.
【详解】(1)解:∵,
∴,
∵平分,
∴,
∵,
∴;
故答案为:25,40
(2)证明:∵平分,
∴,
∵,
∴,
∵
∴
∵
∴;
(3)解:①当点在线段的左侧时,如图,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵平分,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴;
②当点在线段的右侧时,如图,
∵,
∴,
∵,
∴,
∵,
∴,
∴.
∵平分,
∴,
∵,
∴,
∵
∴,
∵,
∴
∵,
∴
∴;
综上,之间的等量关系为:或
【点睛】本题考查平行线的性质,角平分线的定义,角的和差,三角形的内角和定理,综合运用相关知识,掌握分类讨论思想是解题的关键.
知识点2:直角三角形的性质与判定
(1)直角三角形的两个锐角互余.
(2)有两个角互余的三角形是直角三角形.
【提示】直角三角形的性质和判定的应用思路:
(1)见直角三角形,可得两锐角互余.
(2)见两角互余,可得直角三角形.
【题型9 由直角三角形的性质求角度】
【例9】(23-24八年级·河南郑州·期中)在直角三角形中,比的3倍还多,则的大小为 .
【答案】或
【分析】本题主要考查了直角三角形两锐角互余,解题的关键是注意进行分类讨论,分两种情况:当为直角时,当为直角时,分别求出结果即可.
【详解】解:当为直角时,,
当为直角时,,
∵比的3倍还多,
∴,
∴,
∴,
∴,
故答案为:或.
【变式9-1】(23-24八年级·河南南阳·期末)一副三角板按如图所示放置,点在上,点在上,若,则 .
【答案】/110度
【分析】本题考查了直角三角形两锐角互余,对顶角的性质,余角性质,邻补角的性质,由直角三角形两锐角互余可得,,进而由余角性质可得,即可得到,再利用邻补角的性质即可求解,正确识图是解题的关键.
【详解】解:如图,∵,
∴,,
∵,
∴,
∵,
∴,
∴,
故答案为:.
【变式9-2】(23-24八年级·湖南株洲·期中)如图,在中,,,于D,于E,与交于H,则 .
【答案】
【分析】本题考查直角三角形两个锐角互余,三角形的高的性质等知识,延长交于点M,可得在中,三边所在的高交于一点,即,由此即可解答.
【详解】解:延长交于点M,如图,
在中,三边所在的高交于一点,
∴,
∵,
∴,
故答案为:.
【变式9-3】(23-24八年级·四川成都·期末)如图,有一副三角板ABC与DEF,其中∠C=∠F=90°,∠A=60°,∠D=45°,在一平面内将这副三角板进行拼摆,使得点B、E重合,且点B、C、F三点在同一直线上,则∠ABD的度数是 °.
【答案】15°或105°或75°或165
【分析】根据题意画出四种情况,先根据直角三角形的两锐角互余求出∠ABC和∠DEF的度数,再分别求出∠ABD即可.
【详解】解:有四种情况:
第一种情况:如图1,
∵∠C=∠F=90°,∠A=60°,∠D=45°,
∴∠ABC=90°-∠A=30°,∠DBF=90°-∠D=45°,
∴∠ABD=∠DBF-∠ABC=45°-30°=15°;
第二种情况:如图2,
∵∠ABC=30°,∠DEF=45°,
∴∠ABD=1800°-∠ABC-∠DEF=180°-30°-45°=105°;
第三种情况:如图3,
∵∠ABC=30°,∠DEF=45°,
∴∠ABD=∠ABC+∠DEF=30°+45°=75°;
第四种情况:如图4,
∵∠DEF=45°,
∴∠DBC=180°-∠DEF=135°,
∵∠ABC=30°,
∴∠ABD=∠ABC+∠DBC=30°+135°=165°;
∠ABD的度数是15°或105°或75°或165°,
故答案为:15°或105°或75°或165.
【点睛】本题考查了直角三角形的性质和三角形内角和定理,能正确画出符合的所有图形是解此题的关键.
【题型10 锐角互余的三角形是直角三角形】
【例10】(23-24八年级·全国·课堂例题)如图,在中,是边上的高,E是边上一点,交于点M,且.求证:是直角三角形.
【答案】见解析
【分析】本题考查了直角三角形的性质与判定;由是边上的高,得;再由,即可得结论成立.
【详解】解:∵是边上的高,
∴,
∴.
∵,
∴,
∴是直角三角形.
【变式10-1】(23-24八年级·江苏南京·期中)证明:有两个角互余的三角形是直角三角形.
已知:如图, ,
求证: .
证明:
【答案】见解析
【分析】本题考查了直角三角形的性质,三角形内角和定理,熟练运用三角形内角和定理是本题的关键.利用三角形的内角和定理求解即可.
【详解】已知:在中,,
求证:是直角三角形,
证明:在中,(三角形三个内角的和等于).
(等式性质).
(已知),
(等量代换),
是直角三角形.
【变式10-2】(23-24八年级·河南周口·阶段练习)在下列条件中:①,②,③,④中,能确定是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】本题考查了三角形内角和定理,以及三角形的形状判定,根据直角三角形的判定方法对各个选项进行分析,从而得到答案.
【详解】解:①因为,则,所以是直角三角形;
②因为,设,则,,,所以是直角三角形;
③因为,所以,则,所以是直角三角形;
④因为,所以,又,,解得,是直角三角形;
能确定是直角三角形的有①②③④共4个,
故选:D.
【变式10-3】(23-24八年级·全国·课后作业)如图,平分,平分,和交于点E.写出图中所有的直角三角形(不要求证明).
【答案】,,
【分析】根据平行线的性质和角平分线的定义,结合三角形的内角和定理证得即可得出结论.
【详解】解:∵,
∴,
∵平分,平分,
∴,,
∴,
∴是直角三角形,
∴,
∵和交于点E,
∴,
∴,,均为直角三角形.
【点睛】本题考查直角三角形的判定,涉及平行线的性质、角平分线的定义、邻补角、锐角互余的三角形是直角三角形等知识,熟练掌握锐角互余的三角形是直角三角形是解答的关键.
21世纪教育网(www.21cnjy.com)
