解直角三角形的应用
图片预览




文档简介
课件19张PPT。解直角三角形的应用目标预览1、能够把实际问题转化成实际问题,并能进行有关三角函数的计算。
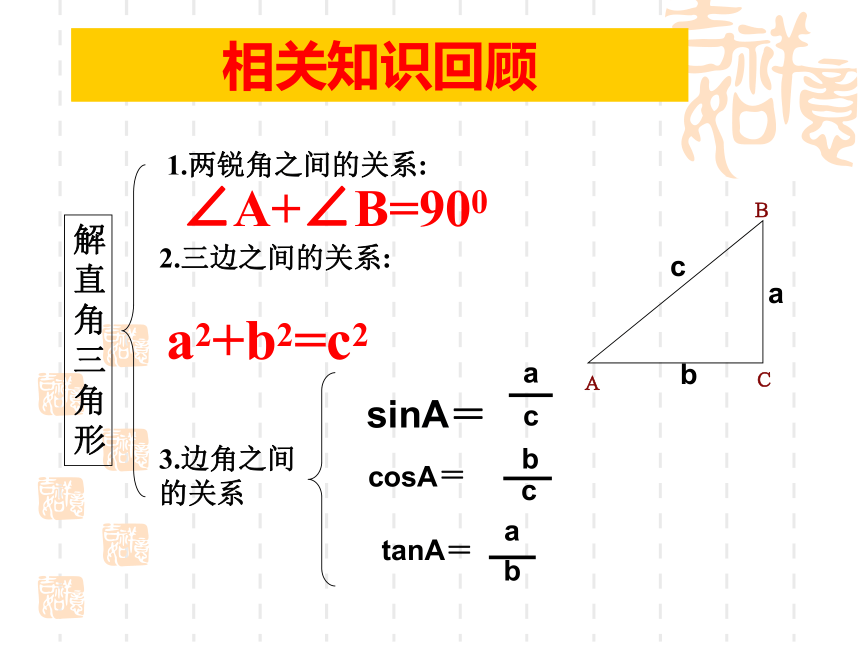
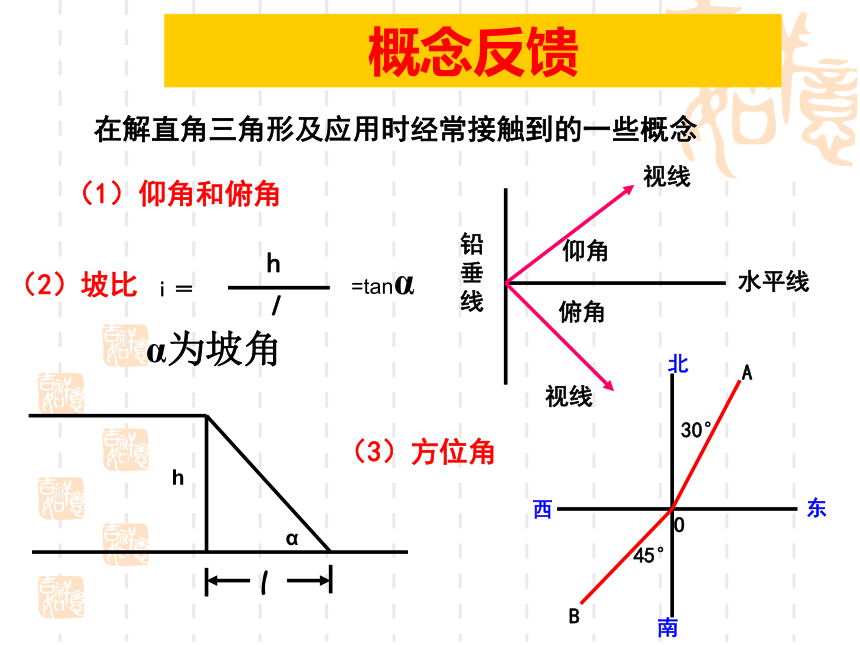
2.具备运用三角函数解决实际问题的能力,发展数学应用意识。解直角三角形1.两锐角之间的关系:2.三边之间的关系:3.边角之间的关系∠A+∠B=900a2+b2=c2sinA=相关知识回顾在解直角三角形及应用时经常接触到的一些概念概念反馈(1)仰角和俯角(3)方位角α为坡角=tanα
如果你站在距塔底部20m处看塔的顶端,视线的仰角为60°,
双眼离地面为1.42m,请根据这些条件求出文光塔的高度。⌒60°1、山坡上种树,要求株距(相临两树间的水平
距离)是5米,测的斜坡倾斜角是30o,求斜坡上相
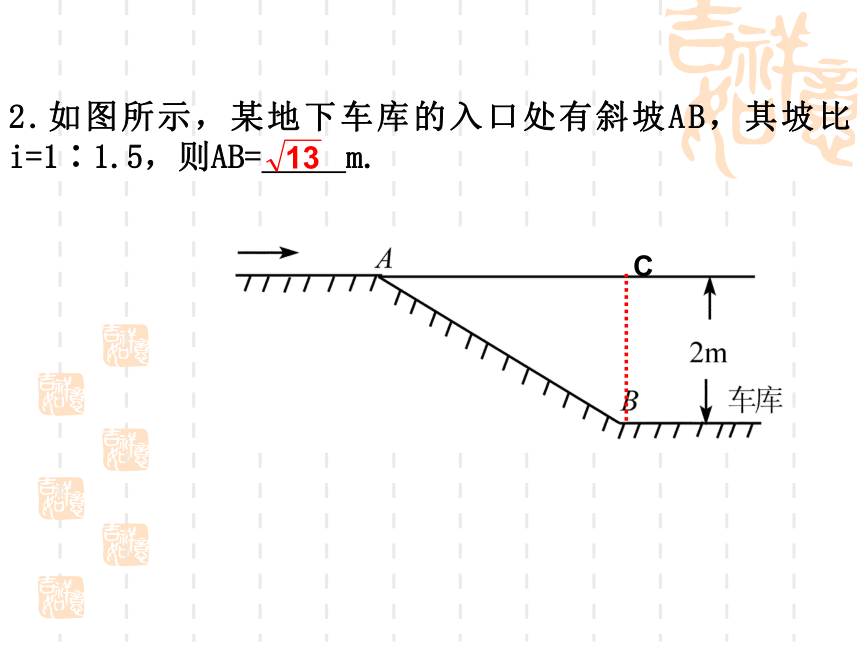
邻两树间的坡面距离是多少米(精确到0.1米)基础练习2.如图所示,某地下车库的入口处有斜坡AB,其坡比i=1∶1.5,则AB= m.C3、如图7-3-3所示,B、C是河对岸的两点,A是对岸岸边一点,测量∠ABC=45°,∠ACB=30°,BC=60米,则点A到BC的距离是 米。(精确到0.01米)图7-3-3 21.96D450300能力提高: 1.如图,灯塔A周围1000米处水域内有礁石,一船艇由西向东航行,在O处测得灯在北偏东600方向线上,这时O、A相距4200米,如果不改变航行方向,此艇是否有触礁的危险?OA2、 如图,温州某公园入口处原有三级台阶,每级台阶高
为30cm,深为30cm.为方便残废人士,现拟将台阶改为斜
坡,设台阶的起始点为A,斜坡的起始点为C,现将斜坡的
坡角∠BCA设计为12°,求AC的长度. (sin12°≈ 0.2079, cos12°≈ 0.9781tan12°≈ 0.2126 ) 解:在Rt△BDC中,∠C=12°∴ AC=282-60=222(cm)由题意得,BD=60 山顶上有一旗杆,在地面上一点A处测得杆顶B的俯角α =600,杆底C的俯角β =450,已知旗杆高BC=20米, 求山高CD。(保留三个有效数字)试一试1 :如图,一艘渔船正以30海里/小时的速度由西向东
赶鱼群,在A处看某小岛C在船的北偏东60°,40海里
后,渔船行止B处,此时看见小岛C在船的北偏东30°.
已知以小岛C为中心,周围10海里以内为我军导弹
部队军事演习的着弹危险区,问这艘渔船继续向东
追赶鱼群,是否有进入危险区的可能?解:设BD=x 海里解:由题意得AB=20,∴AD=20+x在Rt△ACD和 Rt△BCD中,CD=ADtan30°=BDtan60°∴x=10这艘渔船继续向东追赶鱼群,不会进入危险区.2.如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?,航行24海里到C,见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?答:货轮无触礁危险。∵ ∠NBA= 60?, ∠N1BA= 30?,∴ ∠ABC=30?, ∠ACD= 60?,在Rt△ADC中, CD=AD?tan30= 在Rt△ADB中, BD=AD?tan60?= ∵ BD-CD=BC,BC=24 X= ≈12×1.732 =20.784 > 20 解:过点A作AD⊥BC于D,设AD=x∴∴CBAN1ND75°ABC┓D⌒450如图,在△ABC中,已知AC=6,∠C=75°,
∠B=45°,求△ABC的面积。⌒⌒60°6试一试2、外国船只,除特许外,不得进入我国海洋100海里以内的
区域。如图,设A、B是我们的观察站,A和B之间的距离为
160海里,海岸线是过A、B的一条直线。一外国船只在P点,
在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时
是否要向外国船只发出警告,令其退出我国海域.
┓C请你谈谈对本节学习内容的体会和感受。
1、本节例题学习以后,我们可以得到解直角三角形的两种基本图形:2.(1)把实际问题转化成数学问题,这个转化为两个方面:一是将实际问题的图形转化为几何图形,画出正确的平面或截面示意图,二是将已知条件转化为示意图中的边、角或它们之间的关系.
(2)把数学问题转化成解直角三角形问题,如果示意图不是
直角三角形,可添加适当的辅助线,画出直角三角形.
方法小结:课外探究 在数学活动课上,老师带领同学们去测小河宽。
在A处用测角器测得∠DAC=60。然后沿DA方向前进30米至B处,测得∠DBC=30。试问:依据同学们所测得数据,能否求出小河的宽度CD的值呢?如果可以,请你求出小河的宽度;如果不行,请说明理由。CDAB3030°60°图12、在建筑楼梯时,设计者要考虑楼梯的安全程度,如图1,虚线为楼梯的斜度线,斜度线与地板的夹角为倾角θ,一般情况下,倾角θ愈小,楼梯的安全程度愈高。如图2,设计者为提高楼梯的安全程度,要把楼梯的倾角为θ1减至θ2,这样楼梯占用地板的长度由d1增加到d2,已知d1=4m,θ1=45°θ2=30°求楼梯占用地板的长度增加了多少?(精确到0.01, =1.732)?
2.具备运用三角函数解决实际问题的能力,发展数学应用意识。解直角三角形1.两锐角之间的关系:2.三边之间的关系:3.边角之间的关系∠A+∠B=900a2+b2=c2sinA=相关知识回顾在解直角三角形及应用时经常接触到的一些概念概念反馈(1)仰角和俯角(3)方位角α为坡角=tanα
如果你站在距塔底部20m处看塔的顶端,视线的仰角为60°,
双眼离地面为1.42m,请根据这些条件求出文光塔的高度。⌒60°1、山坡上种树,要求株距(相临两树间的水平
距离)是5米,测的斜坡倾斜角是30o,求斜坡上相
邻两树间的坡面距离是多少米(精确到0.1米)基础练习2.如图所示,某地下车库的入口处有斜坡AB,其坡比i=1∶1.5,则AB= m.C3、如图7-3-3所示,B、C是河对岸的两点,A是对岸岸边一点,测量∠ABC=45°,∠ACB=30°,BC=60米,则点A到BC的距离是 米。(精确到0.01米)图7-3-3 21.96D450300能力提高: 1.如图,灯塔A周围1000米处水域内有礁石,一船艇由西向东航行,在O处测得灯在北偏东600方向线上,这时O、A相距4200米,如果不改变航行方向,此艇是否有触礁的危险?OA2、 如图,温州某公园入口处原有三级台阶,每级台阶高
为30cm,深为30cm.为方便残废人士,现拟将台阶改为斜
坡,设台阶的起始点为A,斜坡的起始点为C,现将斜坡的
坡角∠BCA设计为12°,求AC的长度. (sin12°≈ 0.2079, cos12°≈ 0.9781tan12°≈ 0.2126 ) 解:在Rt△BDC中,∠C=12°∴ AC=282-60=222(cm)由题意得,BD=60 山顶上有一旗杆,在地面上一点A处测得杆顶B的俯角α =600,杆底C的俯角β =450,已知旗杆高BC=20米, 求山高CD。(保留三个有效数字)试一试1 :如图,一艘渔船正以30海里/小时的速度由西向东
赶鱼群,在A处看某小岛C在船的北偏东60°,40海里
后,渔船行止B处,此时看见小岛C在船的北偏东30°.
已知以小岛C为中心,周围10海里以内为我军导弹
部队军事演习的着弹危险区,问这艘渔船继续向东
追赶鱼群,是否有进入危险区的可能?解:设BD=x 海里解:由题意得AB=20,∴AD=20+x在Rt△ACD和 Rt△BCD中,CD=ADtan30°=BDtan60°∴x=10这艘渔船继续向东追赶鱼群,不会进入危险区.2.如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?,航行24海里到C,见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?答:货轮无触礁危险。∵ ∠NBA= 60?, ∠N1BA= 30?,∴ ∠ABC=30?, ∠ACD= 60?,在Rt△ADC中, CD=AD?tan30= 在Rt△ADB中, BD=AD?tan60?= ∵ BD-CD=BC,BC=24 X= ≈12×1.732 =20.784 > 20 解:过点A作AD⊥BC于D,设AD=x∴∴CBAN1ND75°ABC┓D⌒450如图,在△ABC中,已知AC=6,∠C=75°,
∠B=45°,求△ABC的面积。⌒⌒60°6试一试2、外国船只,除特许外,不得进入我国海洋100海里以内的
区域。如图,设A、B是我们的观察站,A和B之间的距离为
160海里,海岸线是过A、B的一条直线。一外国船只在P点,
在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时
是否要向外国船只发出警告,令其退出我国海域.
┓C请你谈谈对本节学习内容的体会和感受。
1、本节例题学习以后,我们可以得到解直角三角形的两种基本图形:2.(1)把实际问题转化成数学问题,这个转化为两个方面:一是将实际问题的图形转化为几何图形,画出正确的平面或截面示意图,二是将已知条件转化为示意图中的边、角或它们之间的关系.
(2)把数学问题转化成解直角三角形问题,如果示意图不是
直角三角形,可添加适当的辅助线,画出直角三角形.
方法小结:课外探究 在数学活动课上,老师带领同学们去测小河宽。
在A处用测角器测得∠DAC=60。然后沿DA方向前进30米至B处,测得∠DBC=30。试问:依据同学们所测得数据,能否求出小河的宽度CD的值呢?如果可以,请你求出小河的宽度;如果不行,请说明理由。CDAB3030°60°图12、在建筑楼梯时,设计者要考虑楼梯的安全程度,如图1,虚线为楼梯的斜度线,斜度线与地板的夹角为倾角θ,一般情况下,倾角θ愈小,楼梯的安全程度愈高。如图2,设计者为提高楼梯的安全程度,要把楼梯的倾角为θ1减至θ2,这样楼梯占用地板的长度由d1增加到d2,已知d1=4m,θ1=45°θ2=30°求楼梯占用地板的长度增加了多少?(精确到0.01, =1.732)?
