人教版2024-2025学年八年级数学上册举一反三专题12.5判定两个三角形全等的常用思路【九大题型】(学生版+解析)
文档属性
| 名称 | 人教版2024-2025学年八年级数学上册举一反三专题12.5判定两个三角形全等的常用思路【九大题型】(学生版+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 13:18:54 | ||
图片预览



文档简介
专题12.5 判定两个三角形全等的常用思路【九大题型】
【人教版】
【题型1 已知两边找另一边,用SSS】 1
【题型2 已知两边找夹角,用SAS】 2
【题型3 一直角边一斜边用HL】 3
【题型4 已知边为角的对边找任一角,用AAS】 5
【题型5 已知边为角的邻边找夹角的另一边,用SAS】 6
【题型6 已知边为角的邻边找夹边的另一角,用ASA】 7
【题型7 已知边为角的邻边找边的对角,用AAS】 9
【题型8 已知两角找夹边,用ASA】 10
【题型9 已知两角找任一角的对边,用AAS】 11
知识点:判定两个三角形全等的常用思路
【题型1 已知两边找另一边,用SSS】
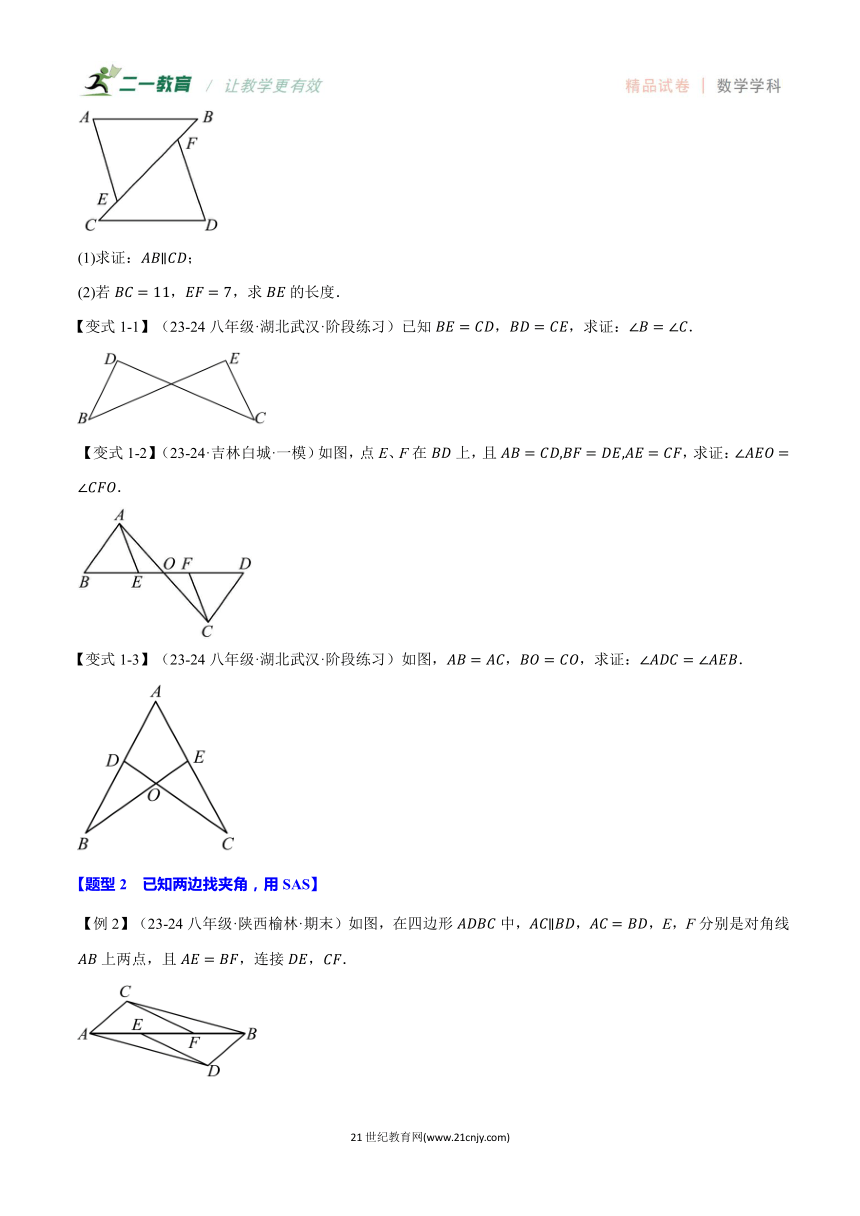
【例1】(23-24八年级·浙江宁波·期末)如图所示,已知,,,且,,,在同一条直线上.
(1)求证:;
(2)若,,求的长度.
【变式1-1】(23-24八年级·湖北武汉·阶段练习)已知,,求证:.
【变式1-2】(23-24·吉林白城·一模)如图,点E、F在上,且,求证:.
【变式1-3】(23-24八年级·湖北武汉·阶段练习)如图,,,求证:.
【题型2 已知两边找夹角,用SAS】
【例2】(23-24八年级·陕西榆林·期末)如图,在四边形中,,,E,F分别是对角线上两点,且,连接.
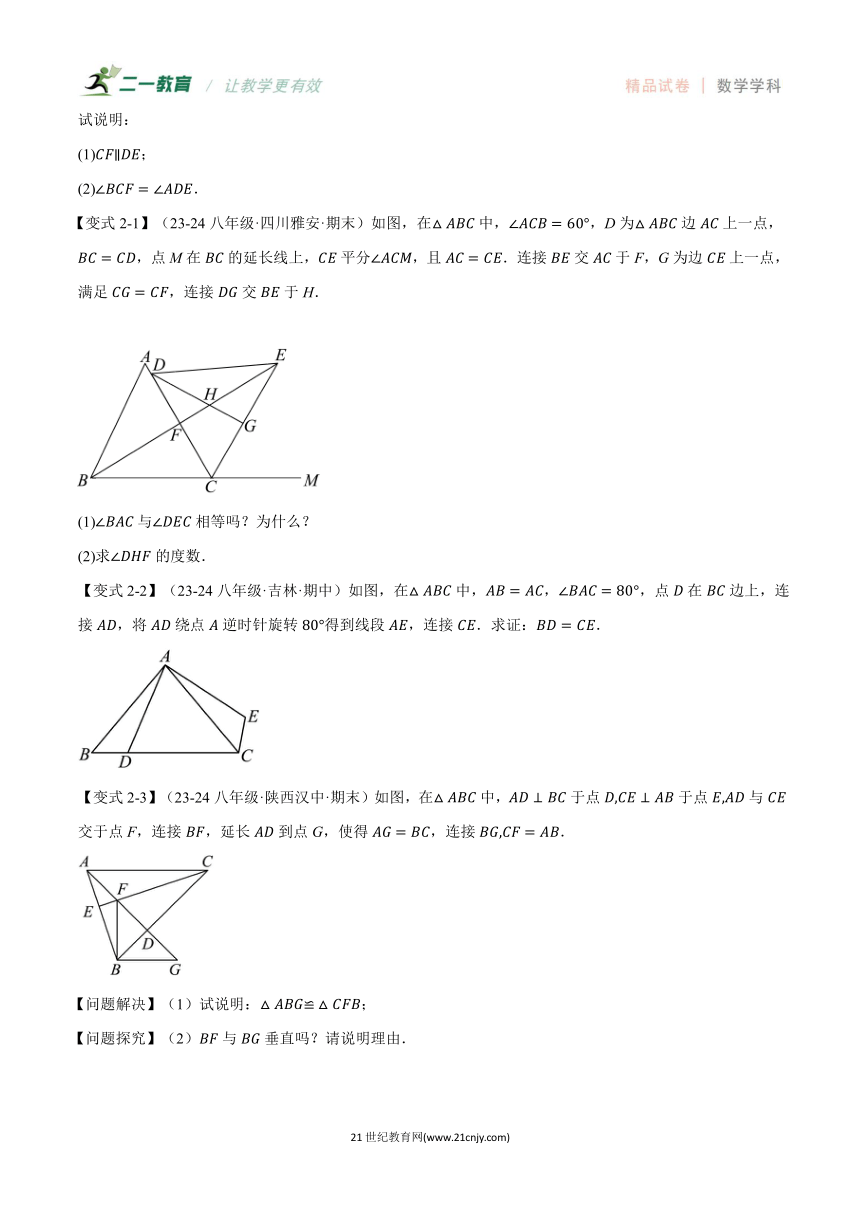
试说明:
(1);
(2).
【变式2-1】(23-24八年级·四川雅安·期末)如图,在中,,D为边上一点,,点M在的延长线上,平分,且.连接交于F,G为边上一点,满足,连接交于H.
(1)与相等吗?为什么?
(2)求的度数.
【变式2-2】(23-24八年级·吉林·期中)如图,在中,,,点在边上,连接,将绕点逆时针旋转得到线段,连接.求证:.
【变式2-3】(23-24八年级·陕西汉中·期末)如图,在中,于点于点与交于点F,连接,延长到点G,使得,连接.
【问题解决】(1)试说明:;
【问题探究】(2)与垂直吗?请说明理由.
【题型3 一直角边一斜边用HL】
【例3】(23-24八年级·河南平顶山·期末)在和中,,,,若边和上的高都是3,,则 .
【变式3-1】(23-24八年级·四川甘孜·期末)如图,已知,,,,与交于点.
(1)求证:.
(2)求.
【变式3-2】(23-24八年级·重庆北碚·期末)如图,在中,于点,点、分别为、上的一点,接并延长交延长线于点,若,,,求证:.
证明:∵
∴
在和中,
∴(② )
∴
在中
∵(③ )
∴
∴④
∴
∵
∴⑤ (⑥ )
∴
∴
【变式3-3】(23-24八年级·重庆·期中)如图,中,,过点作,点P,Q分别在线段和射线上移动.若,则当 时,和全等.
【题型4 已知边为角的对边找任一角,用AAS】
【例4】(23-24八年级·河北唐山·期中)如图,在和中,点,,在同一条直线上,,,若,,则的长为( )
A.8 B.6 C.4 D.2
【变式4-1】(23-24八年级·广东惠州·期中)如图,在和中,,点E是的中点, 于点F,且.
(1)求证:;
(2)若.
①求的长;
②求的面积.
【变式4-2】(23-24·四川达州·模拟预测)如图,在梯形中,,,于点E,,求证.
【变式4-3】(23-24八年级·山西太原·阶段练习)如图,教学楼与操场上的旗杆相距,小林同学从教学楼点沿走到点,一定时间后他到达点,此时他测得和的夹角为,且,已知,旗杆的高为,小林同学行走的速度为.
(1)请你求出教学楼的高度;
(2)小林从点到达点还需要多长时间?
【题型5 已知边为角的邻边找夹角的另一边,用SAS】
【例5】(23-24八年级·广东深圳·期末)如图,中,,以为边向右下方作,满足,点为上一点,连接,若,,,则 .
【变式5-1】(23-24八年级·江苏苏州·期末)如图,在中,为中点,为边上一点,连接,并延长至点 ,使得,连接.
(1)求证:;
(2)若,,,求的度数.
【变式5-2】(23-24八年级·黑龙江哈尔滨·阶段练习)已知,,.
(1)如图1,求证:;
(2)如图2,与相交于点,若,,求的度数.
【变式5-3】(23-24八年级·江西吉安·阶段练习)如图,某游乐园有两个滑梯与,滑梯的高与滑梯水平方向的长度相等,且的长度等于长方形周长的一半.
(1)两个滑梯与的长度是否相等?并说明理由.
(2)若,试说明.
【题型6 已知边为角的邻边找夹边的另一角,用ASA】
【例6】(23-24·四川达州·模拟预测)如图,在梯形中,,,于点E,,求证.
【变式6-1】(23-24·吉林松原·模拟预测)如图,在中,是斜边上的高线,于点F,.求证:.
【变式6-2】(23-24八年级·浙江宁波·期末)如图, 是 的高线,与 相交于点 .若 ,且 的面积为12,则的长度为( )
A.1 B. C.2 D.3
【变式6-3】(23-24八年级·重庆大渡口·阶段练习)如图,在中,,,过点C作,连接.
(1)基本尺规作图:作,交线段于点F(保留作图疯迹);
(2)求证:.
解:∵,
∴________
∵
∴
在和中
∴,
∴(_______)
【题型7 已知边为角的邻边找边的对角,用AAS】
【例7】(23-24八年级·湖北鄂州·期末)如图,中,是边上的中线,过C作,垂足为F,过B作交的延长线于D.
(1)求证:;
(2)若,求的长.
【变式7-1】(23-24八年级·江西吉安·阶段练习)将两个三角形纸板和按如图所示的方式摆放,连接.已知,,.
(1)试说明.
(2)若,求的度数.
【变式7-2】(23-24八年级·四川宜宾·期中)已知:如图,在和中,.求证:
(1);
(2).
【变式7-3】(23-24·黑龙江哈尔滨·一模)如图,在四边形中,于点F,交BC于点G,交的延长线于点E,且.
(1)求证:;
(2)如图2,连接AG,若,请直接写出图2中的三角形,使写出的每个三角形的面积是面积的2倍.
【题型8 已知两角找夹边,用ASA】
【例8】(23-24八年级·陕西西安·期末)如图,,平分,下列结论∶① 平分;②;③;④.其中正确的有( )
A.①③ B.③④ C.①③④ D.②③④
【变式8-1】(23-24八年级·云南昭通·期末)如图,C,F为线段BE上两点,,,.求证:.
【变式8-2】(23-24八年级·辽宁阜新·期末)如图,于点,于点,与交于点,且,.求证:.
【变式8-3】(23-24八年级·黑龙江哈尔滨·期末)在 中, 和 的平分线相交于点 F.
(1)如图1,连接,求证:
(2)如图2,当时,若,求的长.
【题型9 已知两角找任一角的对边,用AAS】
【例9】(23-24八年级·福建三明·期中)如图,在中,,将沿射线的方向平移至,连接,设与的交点为.
(1)若为的中点,求证:;
(2)若平分,求的度数.
【变式9-1】(23-24·陕西西安·三模)如图,点B,F,C,E在一条直线上,点A,D在这条直线的两侧,已知,,.求证:.
【变式9-2】(23-24八年级·浙江金华·阶段练习)如图,在和中,点在同一直线上,,.
(1)求证:;
(2)当时,求的度数.
【变式9-3】(23-24八年级·山东青岛·期末)已知,在中,,.在内部作,交于点D.将一个含有45°角的三角板如图放置,使直角边与重合,三角板沿平移.
(1)如图1,当三角板的另一条直角边过点A时,试证明;
(2)将三角板沿平移至图2的位置,与交于点M,过点M作,垂足为点N,试判断线段之间的关系.21世纪教育网(www.21cnjy.com)
专题12.5 判定两个三角形全等的常用思路【九大题型】
【人教版】
【题型1 已知两边找另一边,用SSS】 1
【题型2 已知两边找夹角,用SAS】 4
【题型3 一直角边一斜边用HL】 8
【题型4 已知边为角的对边找任一角,用AAS】 13
【题型5 已知边为角的邻边找夹角的另一边,用SAS】 17
【题型6 已知边为角的邻边找夹边的另一角,用ASA】 21
【题型7 已知边为角的邻边找边的对角,用AAS】 25
【题型8 已知两角找夹边,用ASA】 31
【题型9 已知两角找任一角的对边,用AAS】 35
知识点:判定两个三角形全等的常用思路
【题型1 已知两边找另一边,用SSS】
【例1】(23-24八年级·浙江宁波·期末)如图所示,已知,,,且,,,在同一条直线上.
(1)求证:;
(2)若,,求的长度.
【答案】(1)见解析
(2)9
【分析】本题考查了全等三角形的判定与性质,平行线的判定,线段的和与差.熟练掌握全等三角形的判定与性质,平行线的判定,线段的和与差是解题的关键.
(1)证明,则,进而可证;
(2)由题意得,,由,可得,根据,计算求解即可.
【详解】(1)证明:∵,
∴,即,
∵,,,
∴,
∴,
∴;
(2)解:∵,,
∴,
∵,
∴,
∴,
∴的长度为9.
【变式1-1】(23-24八年级·湖北武汉·阶段练习)已知,,求证:.
【答案】证明见详解;
【分析】
本题考查三角形全等的判定与性质,连接,根据边边边判定证明即可得到答案;
【详解】
证明:连接,
在与中,
∵,
∴,
,
∴.
【变式1-2】(23-24·吉林白城·一模)如图,点E、F在上,且,求证:.
【答案】见解析
【分析】本题考查全等三角形的判定和性质,根据,得,利用证,再利用全等三角形性质即可证明结论,明解题的关键是学会利用全等三角形解决问题.
【详解】证明:,
,即,
在和中,
,
,
,
.
【变式1-3】(23-24八年级·湖北武汉·阶段练习)如图,,,求证:.
【答案】见解析
【分析】本题考查了全等三角形的判定与性质、三角形外角的定义及性质,连接,证明得出,再由三角形外角的定义及性质即可得出答案,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】证明:如图,连接,
在和中,
,
∴,
∴,
∵,
∴,
∴.
【题型2 已知两边找夹角,用SAS】
【例2】(23-24八年级·陕西榆林·期末)如图,在四边形中,,,E,F分别是对角线上两点,且,连接.
试说明:
(1);
(2).
【答案】(1)见解析
(2)见解析
【分析】本题考查了全等三角形的判定与性质,证明三角形全等是解题的关键.
(1)由证明即可;
(2)由证明即可.
【详解】(1)解:因为,
即,
所以,
因为.
所以,
在和中,
所以,
所以,,
所以.
(2)解:因为,
所以,
在和中,
所以,
所以.
【变式2-1】(23-24八年级·四川雅安·期末)如图,在中,,D为边上一点,,点M在的延长线上,平分,且.连接交于F,G为边上一点,满足,连接交于H.
(1)与相等吗?为什么?
(2)求的度数.
【答案】(1)相等,理由见解析
(2)
【分析】本题考查全等三角形的判定和性质、三角形内角和定理的应用:
(1)先求出,再证 ,可得 ;
(2)先证 ,推出 ,结合 ,可得.
【详解】(1)解:与相等,理由如下:
,平分,
,
在与中,
,
,
;
(2)解:在与中,
,
,
,
又 ,
.
【变式2-2】(23-24八年级·吉林·期中)如图,在中,,,点在边上,连接,将绕点逆时针旋转得到线段,连接.求证:.
【答案】证明见解析.
【分析】本题考查了图形的旋转全等三角形的判定与性质,由旋转性质可知,,则,证明即可,熟练掌握全等三角形的判定与性质是解题的关键.
【详解】证明:由旋转性质可知,,
∴,
∴,即,
在和中,
,
∴,
∴.
【变式2-3】(23-24八年级·陕西汉中·期末)如图,在中,于点于点与交于点F,连接,延长到点G,使得,连接.
【问题解决】(1)试说明:;
【问题探究】(2)与垂直吗?请说明理由.
【答案】(1)见解析;(2)与垂直,理由见解析
【分析】本题考查了全等三角形的判定和性质,垂直的定义,三角形的内角和定理.
(1)根据得出,根据得出,即可推出,最后即可根据得出;
(2)根据垂直的定义得出,根据全等三角形的性质得出,则,即可得出结论.
【详解】(1)证明:∵,
∴,则,
∵,
∴,则,
∴,
在和中,
,
∴.
(2)解:与垂直,理由如下:
∵,
∴,则,
由(1)可得:,
∴,
∴,即,
∴.
【题型3 一直角边一斜边用HL】
【例3】(23-24八年级·河南平顶山·期末)在和中,,,,若边和上的高都是3,,则 .
【答案】或
【分析】本题考查了全等三角形的判定和性质,分类讨论是解题的关键.过A作于点D,过作于点,可得,分四种情况讨论,利用全等三角形的判定和性质即可求解.
【详解】解:过A作于点D,过作于点,
∵边和上的高都是3,
∴,
当在点D的两侧,在点的两侧时,如图,
∵,,
∴,
∴;
当在点D的同侧,在点的同侧时,如图,
同理可得:,;
当在点D的两侧,在点的同侧时,如图,
∵,,
∴,
∴,即;
当在点D的同侧,在点的两侧时,如图,
同理可得:;
综上,的值为或.
故答案为:或.
【变式3-1】(23-24八年级·四川甘孜·期末)如图,已知,,,,与交于点.
(1)求证:.
(2)求.
【答案】(1)证明见解析
(2)
【分析】本题考查全等三角形的性质和判定,三角形外角的性质,
(1)根据证明两个三角形全等即可;
(2)根据三角形全等的性质和三角形外角的性质可得结论;
解题的关键是掌握三角形全等的判定.
【详解】(1)证明:∵,
∴,即,
∵,
在和中,
,
∴;
(2)解:∵,,
∴,
由(1)知:,
∴,
∴,
∴,
∴的度数为.
【变式3-2】(23-24八年级·重庆北碚·期末)如图,在中,于点,点、分别为、上的一点,接并延长交延长线于点,若,,,求证:.
证明:∵
∴
在和中,
∴(② )
∴
在中
∵(③ )
∴
∴④
∴
∵
∴⑤ (⑥ )
∴
∴
【答案】;;三角形的内角和定理,;;同旁内角互补,两直线平行.
【分析】本题考查了平行线的判定和性质,垂线的定义,灵活运用平行线的判定和性质得出角的关系式解题的关键.根据全等三角形的判定及性质,平行线的判定及性质以及垂线定义判断求解即可.
【详解】解:证明:∵
∴
在和中,
∴()
∴
在中
∵(三角形的内角和定理)
∴
∴
∴
∵
∴ 同旁内角互补,两直线平行
∴
∴
故答案为:;;三角形的内角和定理,;;同旁内角互补,两直线平行.
【变式3-3】(23-24八年级·重庆·期中)如图,中,,过点作,点P,Q分别在线段和射线上移动.若,则当 时,和全等.
【答案】或
【分析】本题考查了三角形全等的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键,注意分类讨论,以免漏解.分情况讨论:①时,;②当P运动到与C点重合时,,此时.
【详解】解:①当P运动到时,如图所示:
在和中,
,
∴,
即;
②当P运动到与C点重合时,如图所示:
在和中,
,
∴),
即.
综上所述,的长度是或.
故答案为:或.
【题型4 已知边为角的对边找任一角,用AAS】
【例4】(23-24八年级·河北唐山·期中)如图,在和中,点,,在同一条直线上,,,若,,则的长为( )
A.8 B.6 C.4 D.2
【答案】C
【分析】本题考查了三角形全等的判定与性质,根据三角形内角和定理,证明,由即可求出结果.
【详解】解:,,
,
,
,
在和中,
,
,
,
,,
,
故选:C.
【变式4-1】(23-24八年级·广东惠州·期中)如图,在和中,,点E是的中点, 于点F,且.
(1)求证:;
(2)若.
①求的长;
②求的面积.
【答案】(1)见解析
(2)①6;②36
【分析】本题考查了全等三角形的判定与性质.熟练掌握全等三角形的判定条件是解题的关键.
(1)由题意知,,,则,证明;
(2)①由题意知,,由,可得,计算求解即可;②根据,计算求解即可.
【详解】(1)证明:∵,
∴,
∵,
∴,即,
∴,
∵,,,
∴;
(2)①解:∵点E是的中点,
∴,
由(1)可知,,
∴,
∴,
∴的长为6;
②解:由题意知,,
∴的面积为36.
【变式4-2】(23-24·四川达州·模拟预测)如图,在梯形中,,,于点E,,求证.
【答案】见解析
【分析】本题主要考查全等三角形的判定以及平行线的性质,熟练掌握全等三角形的判定是解题的关键.根据题意证明,根据即可得到答案.
【详解】证明:,
,
,
,
,
,
,
在和中,
,
.
【变式4-3】(23-24八年级·山西太原·阶段练习)如图,教学楼与操场上的旗杆相距,小林同学从教学楼点沿走到点,一定时间后他到达点,此时他测得和的夹角为,且,已知,旗杆的高为,小林同学行走的速度为.
(1)请你求出教学楼的高度;
(2)小林从点到达点还需要多长时间?
【答案】(1)
(2)
【分析】本题考查的是全等三角形的判定与性质,熟记全等三角形的判定方法是解本题的关键;
(1)先证明,再结合,即可得到结论;
(2)利用路程除以速度即可得到答案.
【详解】(1)解:∵和的夹角为,
∴.
∵,
∴,
∴.
在和中,
,
∴,
∴,.
∵,
∴.
∵,
∴,
∴.
答:教学楼的高度为.
(2).
答:小林从点到达点还需要.
【题型5 已知边为角的邻边找夹角的另一边,用SAS】
【例5】(23-24八年级·广东深圳·期末)如图,中,,以为边向右下方作,满足,点为上一点,连接,若,,,则 .
【答案】5
【分析】本题考查全等三角形的判定与性质,正确作出辅助线,构造全等三角形是解题的关键.
延长到E,使,连接,先证明,得到,,再证明,得到,即可由,进而即可求解.
【详解】解:延长到E,使,连接,如图,
∵,,,
∴,
∴,,
∴,
∵,
∴,
∴,
∴,
在与中,
,
∴,
∴,
∴.
故答案为:5.
【变式5-1】(23-24八年级·江苏苏州·期末)如图,在中,为中点,为边上一点,连接,并延长至点 ,使得,连接.
(1)求证:;
(2)若,,,求的度数.
【答案】(1)证明见解析;
(2).
【分析】()由为中点得,然后用“”证明即可;
()由,得, 三角形的内角和得,最后由平行线的性质即可求解;
本题考查了全等三角形的判定与性质,平行线的性质,三角形的内角和,熟练掌握知识点的应用是解题的关键.
【详解】(1)证明:∵为中点,
∴,
在和中,
,
∴;
(2)由()得:,
∴,
∵,,
∴,
∵,
∴.
【变式5-2】(23-24八年级·黑龙江哈尔滨·阶段练习)已知,,.
(1)如图1,求证:;
(2)如图2,与相交于点,若,,求的度数.
【答案】(1)证明见解析
(2)
【分析】
本题考查三角形全等的判定与性质、三角形外角性质及三角形内角和定理等知识,熟练掌握三角形全等的判定与性质是解决问题的关键.
(1)利用三角形全等判定与性质,证得,即可得证;
(2)利用全等三角形性质得到,再由三角形外角性质与三角形内角和定理数形结合即可得到答案.
【详解】(1)证明: ,,
,
在和中,
,
;
(2)解:由(1)知,,
在中,是其外角,则,
在中,.
【变式5-3】(23-24八年级·江西吉安·阶段练习)如图,某游乐园有两个滑梯与,滑梯的高与滑梯水平方向的长度相等,且的长度等于长方形周长的一半.
(1)两个滑梯与的长度是否相等?并说明理由.
(2)若,试说明.
【答案】(1)相等,理由见解析
(2)见解析
【分析】本题考查了全等三角形的应用;确定两角的大小关系,通常可证明这两角所在的三角形全等,根据对应角相等进行判定.
(1)根据的长度等于长方形周长的一半,得出,证明,即可证明;
(2)根据全等三角形的性质得出,结合,得出,证出,即可证明;
【详解】(1)解:.
理由:∵的长度等于长方形周长的一半,
∴,
∴.
在和中,
,
∴,
∴.
(2)∵,
∴.
∵,
∴,
∴.
∵,
∴,
∴.
【题型6 已知边为角的邻边找夹边的另一角,用ASA】
【例6】(23-24·四川达州·模拟预测)如图,在梯形中,,,于点E,,求证.
【答案】见解析
【分析】本题主要考查全等三角形的判定以及平行线的性质,熟练掌握全等三角形的判定是解题的关键.根据题意证明,根据即可得到答案.
【详解】证明:,
,
,
,
,
,
,
在和中,
,
.
【变式6-1】(23-24·吉林松原·模拟预测)如图,在中,是斜边上的高线,于点F,.求证:.
【答案】见解析
【分析】本题主要考查全等三角形的判定,熟练掌握全等三角形的判定是解题的关键.根据题意,利用证明即可.
【详解】证明:在中,.
,
.
.
,
.
在和中,
,
.
【变式6-2】(23-24八年级·浙江宁波·期末)如图, 是 的高线,与 相交于点 .若 ,且 的面积为12,则的长度为( )
A.1 B. C.2 D.3
【答案】C
【分析】本题主要考查了全等三角形的判定与性质,三角形的面积等知识,熟练掌握全等三角形的判定与性质是解题的关键.利用证明,得,再根据三角形面积可得的长,从而可得答案.
【详解】解:∵,是的高线,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵的面积为12,
∴,
∴,
∴,
∴,
故选:C.
【变式6-3】(23-24八年级·重庆大渡口·阶段练习)如图,在中,,,过点C作,连接.
(1)基本尺规作图:作,交线段于点F(保留作图疯迹);
(2)求证:.
解:∵,
∴________
∵
∴
在和中
∴,
∴(_______)
【答案】(1)见解析
(2)见解析
【分析】(1)根据运用作相等角的作图方法画图即可;
(2)根据平行线的性质可推出①及②,再根据全等三角形的判定定理和性质可得③④.
【详解】(1)解:如图:即为所求;
(2)解:∵
∴(两直线平行,同旁内角互补)
∵
∴
在和中
∴
∴(全等三角形的对应边相等).
【题型7 已知边为角的邻边找边的对角,用AAS】
【例7】(23-24八年级·湖北鄂州·期末)如图,中,是边上的中线,过C作,垂足为F,过B作交的延长线于D.
(1)求证:;
(2)若,求的长.
【答案】(1)见解析
(2)
【分析】(1)证两条线段相等,通常用全等,本题中的和分别在和中,在这两个三角形中,已经有一组边相等,一组角相等了,因此只需再找一组角即可利用角角边进行解答.
(2)由(1)得,且,即可求出的长.
【详解】(1)∵,
∴.
∴.
在和中,
∵
∴.
∴.
(2)∵,
∴,
∵是边上的中线,
∴,且.
∴.
【点睛】三角形全等的判定一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
【变式7-1】(23-24八年级·江西吉安·阶段练习)将两个三角形纸板和按如图所示的方式摆放,连接.已知,,.
(1)试说明.
(2)若,求的度数.
【答案】(1)见解析
(2)
【分析】(1)利用证明三角形全等即可;
(2)全等三角形的性质,得到,证明,得到,即可得解.
【详解】(1)解:因为,
所以,
即.
在和中,
,
所以.
(2)因为,
所以,.
在和中,
,
所以,
所以,
所以.
【点睛】本题考查全等三角形的判定和性质.解题的关键是证明三角形全等.
【变式7-2】(23-24八年级·四川宜宾·期中)已知:如图,在和中,.求证:
(1);
(2).
【答案】(1)见解析
(2)见解析
【分析】本题考查了三角形的全等判定和性质,熟练掌握判定定理是解题的关键.
(1)根据得到即,证明即可.
(2)根据得到,结合,得到即,证明即可.
【详解】(1)∵,
∴,
∴,
∵,
∴,
∴.
(2)∵
∴,
∵,
∴,
∴,
∵,
∴.
【变式7-3】(23-24·黑龙江哈尔滨·一模)如图,在四边形中,于点F,交BC于点G,交的延长线于点E,且.
(1)求证:;
(2)如图2,连接AG,若,请直接写出图2中的三角形,使写出的每个三角形的面积是面积的2倍.
【答案】(1)见详解
(2)
【分析】本题考查了全等三角形的判定与性质,以及共高三角形面积比等于底之比,熟练掌握基本知识是解题的关键;
(1)用即可证明;
(2)先证明,则,再证明,则,由与同底等高,得,再证明,则,最后与同底等高,
得,所以.
【详解】(1)证明:∵
∴
∴在和中,
,
∴;
(2)
∵
∴,
∵,
∴,
∴
∵,
∴
∵,
∴,
∴,
∴,
∵,
∴,
∴
∵ ,,
∴,
∴
∵
∴与同底等高,
∴,
∴
∵,∴,
∴,
∴,
∴,∵,
∴,
∴,
∵
∴与同底等高,
∴,
∴,
∴的面积为面积的2倍.
【题型8 已知两角找夹边,用ASA】
【例8】(23-24八年级·陕西西安·期末)如图,,平分,下列结论∶① 平分;②;③;④.其中正确的有( )
A.①③ B.③④ C.①③④ D.②③④
【答案】C
【分析】题目主要考查全等三角形的判定和性质,平行线的性质,理解题意,结合图形求解是解题关键.
根据平行线的性质及各角之间的等量代换得出,再由角平分线及等量代换可判断①;根据全等三角形的判定和性质可判断②和④;利用三角形面积的关系可判断③,即可得出结果.
【详解】解:∵ ,
∴
,
∵ 平分,
,
∴ 平分,故①正确;
在上截取,连接,
在和中,
∴
,
在和中,
,,
故②不正确,④正确;
,
∴,
故③正确;
故选:C.
【变式8-1】(23-24八年级·云南昭通·期末)如图,C,F为线段BE上两点,,,.求证:.
【答案】见解析
【分析】本题考查全等三角形的判定和性质,先由证明,再证,即可证明 ,由此可得.
【详解】证明: ,
,
,
,即,
在和中,
,
,
.
【变式8-2】(23-24八年级·辽宁阜新·期末)如图,于点,于点,与交于点,且,.求证:.
【答案】证明见解析
【分析】本题主要考查了全等三角形的性质与判定,先利用证明得到,进而利用证明,即可证明.
【详解】证明:,,
.
,
,即,
又∵,即
,
∴,
在与中,
,
,
.
【变式8-3】(23-24八年级·黑龙江哈尔滨·期末)在 中, 和 的平分线相交于点 F.
(1)如图1,连接,求证:
(2)如图2,当时,若,求的长.
【答案】(1)见解析
(2)7
【分析】本题主要考查了角平分线的性质,三角形内角和定理,全等三角形的判定和性质:
(1)在中,根据三角形内角和定理可得,再由角平分线的定义可得,从而得到,即可解答;
(2)连接,在上截取,连接,由(1)得:,从而得到,,再证明,可得,从而得到,可证明,从而得到,即可求解.
【详解】(1)证明:在中, ,
∵和 的平分线相交于点 F.
∴,,
∴,
∴,
∴,
∴;
(2)解:如图,连接,在上截取,连接,
由(1)得:,
∵,
∴,
∴,
∴,
∵平分,
∴,
∵,,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴.
【题型9 已知两角找任一角的对边,用AAS】
【例9】(23-24八年级·福建三明·期中)如图,在中,,将沿射线的方向平移至,连接,设与的交点为.
(1)若为的中点,求证:;
(2)若平分,求的度数.
【答案】(1)见解析
(2)
【分析】本题主要考查几何变换,平移的性质,全等三角形的判定和性质,等腰三角形的性质,掌握和理解这些性质进行推理是解题的关键.
(1)根据平移性质得到,,从而得到,再根据为的中点,得到,从而证明结论;
(2)根据平分,得到,从而证明.再根据三角形内角和定理以及,即可求解;
【详解】(1)解:由沿射线的方向平移所得,
,,
,
为的中点,
,
.
在和中
,
;
(2)平分,
,
又,
.
,,
.
【变式9-1】(23-24·陕西西安·三模)如图,点B,F,C,E在一条直线上,点A,D在这条直线的两侧,已知,,.求证:.
【答案】见解析
【分析】此题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键:先推出,由此证得,得到,即可推出.
【详解】证明:∵,
∴,
∴,
在和中,
∴,
∴,
∴.
【变式9-2】(23-24八年级·浙江金华·阶段练习)如图,在和中,点在同一直线上,,.
(1)求证:;
(2)当时,求的度数.
【答案】(1)证明见解析;
(2).
【分析】()由可得,利用即可证明;
(),可得,即可求解;
本题考查了全等三角形的判定和性质,三角形内角和定理,掌握全等三角形的判定和性质是解题的关键.
【详解】(1)证明:∵,
∴,
即,
在和中,
,
∴;
(2)解:∵,,
∴,
∵
∴.
【变式9-3】(23-24八年级·山东青岛·期末)已知,在中,,.在内部作,交于点D.将一个含有45°角的三角板如图放置,使直角边与重合,三角板沿平移.
(1)如图1,当三角板的另一条直角边过点A时,试证明;
(2)将三角板沿平移至图2的位置,与交于点M,过点M作,垂足为点N,试判断线段之间的关系.
【答案】(1)见解析
(2)
【分析】(1)根据等腰三角形的性质得到,根据全等三角形的性质即可得到结论;
(2)过A作于P,于Q,则四边形是矩形,根据矩形的性质得到,,根据平行线的性质得到,得到,由(1)知,,等量代换得到,于是得到结论.
【详解】(1)证明:∵,
∴,
在与中,
,
∴,
∴;
(2).
理由:过A作于P,于Q,
则四边形是长方形
,,
∴,
∵,
∴,
∵,
∴,
由(1)知,,
∴,
∵,
∴.
【点睛】本题考查了作图一平移变换,全等三角形的判定和性质,等腰三角形的性质,矩形的判定和性质,正确地作出辅助线是解题的关键.
21世纪教育网(www.21cnjy.com)
【人教版】
【题型1 已知两边找另一边,用SSS】 1
【题型2 已知两边找夹角,用SAS】 2
【题型3 一直角边一斜边用HL】 3
【题型4 已知边为角的对边找任一角,用AAS】 5
【题型5 已知边为角的邻边找夹角的另一边,用SAS】 6
【题型6 已知边为角的邻边找夹边的另一角,用ASA】 7
【题型7 已知边为角的邻边找边的对角,用AAS】 9
【题型8 已知两角找夹边,用ASA】 10
【题型9 已知两角找任一角的对边,用AAS】 11
知识点:判定两个三角形全等的常用思路
【题型1 已知两边找另一边,用SSS】
【例1】(23-24八年级·浙江宁波·期末)如图所示,已知,,,且,,,在同一条直线上.
(1)求证:;
(2)若,,求的长度.
【变式1-1】(23-24八年级·湖北武汉·阶段练习)已知,,求证:.
【变式1-2】(23-24·吉林白城·一模)如图,点E、F在上,且,求证:.
【变式1-3】(23-24八年级·湖北武汉·阶段练习)如图,,,求证:.
【题型2 已知两边找夹角,用SAS】
【例2】(23-24八年级·陕西榆林·期末)如图,在四边形中,,,E,F分别是对角线上两点,且,连接.
试说明:
(1);
(2).
【变式2-1】(23-24八年级·四川雅安·期末)如图,在中,,D为边上一点,,点M在的延长线上,平分,且.连接交于F,G为边上一点,满足,连接交于H.
(1)与相等吗?为什么?
(2)求的度数.
【变式2-2】(23-24八年级·吉林·期中)如图,在中,,,点在边上,连接,将绕点逆时针旋转得到线段,连接.求证:.
【变式2-3】(23-24八年级·陕西汉中·期末)如图,在中,于点于点与交于点F,连接,延长到点G,使得,连接.
【问题解决】(1)试说明:;
【问题探究】(2)与垂直吗?请说明理由.
【题型3 一直角边一斜边用HL】
【例3】(23-24八年级·河南平顶山·期末)在和中,,,,若边和上的高都是3,,则 .
【变式3-1】(23-24八年级·四川甘孜·期末)如图,已知,,,,与交于点.
(1)求证:.
(2)求.
【变式3-2】(23-24八年级·重庆北碚·期末)如图,在中,于点,点、分别为、上的一点,接并延长交延长线于点,若,,,求证:.
证明:∵
∴
在和中,
∴(② )
∴
在中
∵(③ )
∴
∴④
∴
∵
∴⑤ (⑥ )
∴
∴
【变式3-3】(23-24八年级·重庆·期中)如图,中,,过点作,点P,Q分别在线段和射线上移动.若,则当 时,和全等.
【题型4 已知边为角的对边找任一角,用AAS】
【例4】(23-24八年级·河北唐山·期中)如图,在和中,点,,在同一条直线上,,,若,,则的长为( )
A.8 B.6 C.4 D.2
【变式4-1】(23-24八年级·广东惠州·期中)如图,在和中,,点E是的中点, 于点F,且.
(1)求证:;
(2)若.
①求的长;
②求的面积.
【变式4-2】(23-24·四川达州·模拟预测)如图,在梯形中,,,于点E,,求证.
【变式4-3】(23-24八年级·山西太原·阶段练习)如图,教学楼与操场上的旗杆相距,小林同学从教学楼点沿走到点,一定时间后他到达点,此时他测得和的夹角为,且,已知,旗杆的高为,小林同学行走的速度为.
(1)请你求出教学楼的高度;
(2)小林从点到达点还需要多长时间?
【题型5 已知边为角的邻边找夹角的另一边,用SAS】
【例5】(23-24八年级·广东深圳·期末)如图,中,,以为边向右下方作,满足,点为上一点,连接,若,,,则 .
【变式5-1】(23-24八年级·江苏苏州·期末)如图,在中,为中点,为边上一点,连接,并延长至点 ,使得,连接.
(1)求证:;
(2)若,,,求的度数.
【变式5-2】(23-24八年级·黑龙江哈尔滨·阶段练习)已知,,.
(1)如图1,求证:;
(2)如图2,与相交于点,若,,求的度数.
【变式5-3】(23-24八年级·江西吉安·阶段练习)如图,某游乐园有两个滑梯与,滑梯的高与滑梯水平方向的长度相等,且的长度等于长方形周长的一半.
(1)两个滑梯与的长度是否相等?并说明理由.
(2)若,试说明.
【题型6 已知边为角的邻边找夹边的另一角,用ASA】
【例6】(23-24·四川达州·模拟预测)如图,在梯形中,,,于点E,,求证.
【变式6-1】(23-24·吉林松原·模拟预测)如图,在中,是斜边上的高线,于点F,.求证:.
【变式6-2】(23-24八年级·浙江宁波·期末)如图, 是 的高线,与 相交于点 .若 ,且 的面积为12,则的长度为( )
A.1 B. C.2 D.3
【变式6-3】(23-24八年级·重庆大渡口·阶段练习)如图,在中,,,过点C作,连接.
(1)基本尺规作图:作,交线段于点F(保留作图疯迹);
(2)求证:.
解:∵,
∴________
∵
∴
在和中
∴,
∴(_______)
【题型7 已知边为角的邻边找边的对角,用AAS】
【例7】(23-24八年级·湖北鄂州·期末)如图,中,是边上的中线,过C作,垂足为F,过B作交的延长线于D.
(1)求证:;
(2)若,求的长.
【变式7-1】(23-24八年级·江西吉安·阶段练习)将两个三角形纸板和按如图所示的方式摆放,连接.已知,,.
(1)试说明.
(2)若,求的度数.
【变式7-2】(23-24八年级·四川宜宾·期中)已知:如图,在和中,.求证:
(1);
(2).
【变式7-3】(23-24·黑龙江哈尔滨·一模)如图,在四边形中,于点F,交BC于点G,交的延长线于点E,且.
(1)求证:;
(2)如图2,连接AG,若,请直接写出图2中的三角形,使写出的每个三角形的面积是面积的2倍.
【题型8 已知两角找夹边,用ASA】
【例8】(23-24八年级·陕西西安·期末)如图,,平分,下列结论∶① 平分;②;③;④.其中正确的有( )
A.①③ B.③④ C.①③④ D.②③④
【变式8-1】(23-24八年级·云南昭通·期末)如图,C,F为线段BE上两点,,,.求证:.
【变式8-2】(23-24八年级·辽宁阜新·期末)如图,于点,于点,与交于点,且,.求证:.
【变式8-3】(23-24八年级·黑龙江哈尔滨·期末)在 中, 和 的平分线相交于点 F.
(1)如图1,连接,求证:
(2)如图2,当时,若,求的长.
【题型9 已知两角找任一角的对边,用AAS】
【例9】(23-24八年级·福建三明·期中)如图,在中,,将沿射线的方向平移至,连接,设与的交点为.
(1)若为的中点,求证:;
(2)若平分,求的度数.
【变式9-1】(23-24·陕西西安·三模)如图,点B,F,C,E在一条直线上,点A,D在这条直线的两侧,已知,,.求证:.
【变式9-2】(23-24八年级·浙江金华·阶段练习)如图,在和中,点在同一直线上,,.
(1)求证:;
(2)当时,求的度数.
【变式9-3】(23-24八年级·山东青岛·期末)已知,在中,,.在内部作,交于点D.将一个含有45°角的三角板如图放置,使直角边与重合,三角板沿平移.
(1)如图1,当三角板的另一条直角边过点A时,试证明;
(2)将三角板沿平移至图2的位置,与交于点M,过点M作,垂足为点N,试判断线段之间的关系.21世纪教育网(www.21cnjy.com)
专题12.5 判定两个三角形全等的常用思路【九大题型】
【人教版】
【题型1 已知两边找另一边,用SSS】 1
【题型2 已知两边找夹角,用SAS】 4
【题型3 一直角边一斜边用HL】 8
【题型4 已知边为角的对边找任一角,用AAS】 13
【题型5 已知边为角的邻边找夹角的另一边,用SAS】 17
【题型6 已知边为角的邻边找夹边的另一角,用ASA】 21
【题型7 已知边为角的邻边找边的对角,用AAS】 25
【题型8 已知两角找夹边,用ASA】 31
【题型9 已知两角找任一角的对边,用AAS】 35
知识点:判定两个三角形全等的常用思路
【题型1 已知两边找另一边,用SSS】
【例1】(23-24八年级·浙江宁波·期末)如图所示,已知,,,且,,,在同一条直线上.
(1)求证:;
(2)若,,求的长度.
【答案】(1)见解析
(2)9
【分析】本题考查了全等三角形的判定与性质,平行线的判定,线段的和与差.熟练掌握全等三角形的判定与性质,平行线的判定,线段的和与差是解题的关键.
(1)证明,则,进而可证;
(2)由题意得,,由,可得,根据,计算求解即可.
【详解】(1)证明:∵,
∴,即,
∵,,,
∴,
∴,
∴;
(2)解:∵,,
∴,
∵,
∴,
∴,
∴的长度为9.
【变式1-1】(23-24八年级·湖北武汉·阶段练习)已知,,求证:.
【答案】证明见详解;
【分析】
本题考查三角形全等的判定与性质,连接,根据边边边判定证明即可得到答案;
【详解】
证明:连接,
在与中,
∵,
∴,
,
∴.
【变式1-2】(23-24·吉林白城·一模)如图,点E、F在上,且,求证:.
【答案】见解析
【分析】本题考查全等三角形的判定和性质,根据,得,利用证,再利用全等三角形性质即可证明结论,明解题的关键是学会利用全等三角形解决问题.
【详解】证明:,
,即,
在和中,
,
,
,
.
【变式1-3】(23-24八年级·湖北武汉·阶段练习)如图,,,求证:.
【答案】见解析
【分析】本题考查了全等三角形的判定与性质、三角形外角的定义及性质,连接,证明得出,再由三角形外角的定义及性质即可得出答案,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】证明:如图,连接,
在和中,
,
∴,
∴,
∵,
∴,
∴.
【题型2 已知两边找夹角,用SAS】
【例2】(23-24八年级·陕西榆林·期末)如图,在四边形中,,,E,F分别是对角线上两点,且,连接.
试说明:
(1);
(2).
【答案】(1)见解析
(2)见解析
【分析】本题考查了全等三角形的判定与性质,证明三角形全等是解题的关键.
(1)由证明即可;
(2)由证明即可.
【详解】(1)解:因为,
即,
所以,
因为.
所以,
在和中,
所以,
所以,,
所以.
(2)解:因为,
所以,
在和中,
所以,
所以.
【变式2-1】(23-24八年级·四川雅安·期末)如图,在中,,D为边上一点,,点M在的延长线上,平分,且.连接交于F,G为边上一点,满足,连接交于H.
(1)与相等吗?为什么?
(2)求的度数.
【答案】(1)相等,理由见解析
(2)
【分析】本题考查全等三角形的判定和性质、三角形内角和定理的应用:
(1)先求出,再证 ,可得 ;
(2)先证 ,推出 ,结合 ,可得.
【详解】(1)解:与相等,理由如下:
,平分,
,
在与中,
,
,
;
(2)解:在与中,
,
,
,
又 ,
.
【变式2-2】(23-24八年级·吉林·期中)如图,在中,,,点在边上,连接,将绕点逆时针旋转得到线段,连接.求证:.
【答案】证明见解析.
【分析】本题考查了图形的旋转全等三角形的判定与性质,由旋转性质可知,,则,证明即可,熟练掌握全等三角形的判定与性质是解题的关键.
【详解】证明:由旋转性质可知,,
∴,
∴,即,
在和中,
,
∴,
∴.
【变式2-3】(23-24八年级·陕西汉中·期末)如图,在中,于点于点与交于点F,连接,延长到点G,使得,连接.
【问题解决】(1)试说明:;
【问题探究】(2)与垂直吗?请说明理由.
【答案】(1)见解析;(2)与垂直,理由见解析
【分析】本题考查了全等三角形的判定和性质,垂直的定义,三角形的内角和定理.
(1)根据得出,根据得出,即可推出,最后即可根据得出;
(2)根据垂直的定义得出,根据全等三角形的性质得出,则,即可得出结论.
【详解】(1)证明:∵,
∴,则,
∵,
∴,则,
∴,
在和中,
,
∴.
(2)解:与垂直,理由如下:
∵,
∴,则,
由(1)可得:,
∴,
∴,即,
∴.
【题型3 一直角边一斜边用HL】
【例3】(23-24八年级·河南平顶山·期末)在和中,,,,若边和上的高都是3,,则 .
【答案】或
【分析】本题考查了全等三角形的判定和性质,分类讨论是解题的关键.过A作于点D,过作于点,可得,分四种情况讨论,利用全等三角形的判定和性质即可求解.
【详解】解:过A作于点D,过作于点,
∵边和上的高都是3,
∴,
当在点D的两侧,在点的两侧时,如图,
∵,,
∴,
∴;
当在点D的同侧,在点的同侧时,如图,
同理可得:,;
当在点D的两侧,在点的同侧时,如图,
∵,,
∴,
∴,即;
当在点D的同侧,在点的两侧时,如图,
同理可得:;
综上,的值为或.
故答案为:或.
【变式3-1】(23-24八年级·四川甘孜·期末)如图,已知,,,,与交于点.
(1)求证:.
(2)求.
【答案】(1)证明见解析
(2)
【分析】本题考查全等三角形的性质和判定,三角形外角的性质,
(1)根据证明两个三角形全等即可;
(2)根据三角形全等的性质和三角形外角的性质可得结论;
解题的关键是掌握三角形全等的判定.
【详解】(1)证明:∵,
∴,即,
∵,
在和中,
,
∴;
(2)解:∵,,
∴,
由(1)知:,
∴,
∴,
∴,
∴的度数为.
【变式3-2】(23-24八年级·重庆北碚·期末)如图,在中,于点,点、分别为、上的一点,接并延长交延长线于点,若,,,求证:.
证明:∵
∴
在和中,
∴(② )
∴
在中
∵(③ )
∴
∴④
∴
∵
∴⑤ (⑥ )
∴
∴
【答案】;;三角形的内角和定理,;;同旁内角互补,两直线平行.
【分析】本题考查了平行线的判定和性质,垂线的定义,灵活运用平行线的判定和性质得出角的关系式解题的关键.根据全等三角形的判定及性质,平行线的判定及性质以及垂线定义判断求解即可.
【详解】解:证明:∵
∴
在和中,
∴()
∴
在中
∵(三角形的内角和定理)
∴
∴
∴
∵
∴ 同旁内角互补,两直线平行
∴
∴
故答案为:;;三角形的内角和定理,;;同旁内角互补,两直线平行.
【变式3-3】(23-24八年级·重庆·期中)如图,中,,过点作,点P,Q分别在线段和射线上移动.若,则当 时,和全等.
【答案】或
【分析】本题考查了三角形全等的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键,注意分类讨论,以免漏解.分情况讨论:①时,;②当P运动到与C点重合时,,此时.
【详解】解:①当P运动到时,如图所示:
在和中,
,
∴,
即;
②当P运动到与C点重合时,如图所示:
在和中,
,
∴),
即.
综上所述,的长度是或.
故答案为:或.
【题型4 已知边为角的对边找任一角,用AAS】
【例4】(23-24八年级·河北唐山·期中)如图,在和中,点,,在同一条直线上,,,若,,则的长为( )
A.8 B.6 C.4 D.2
【答案】C
【分析】本题考查了三角形全等的判定与性质,根据三角形内角和定理,证明,由即可求出结果.
【详解】解:,,
,
,
,
在和中,
,
,
,
,,
,
故选:C.
【变式4-1】(23-24八年级·广东惠州·期中)如图,在和中,,点E是的中点, 于点F,且.
(1)求证:;
(2)若.
①求的长;
②求的面积.
【答案】(1)见解析
(2)①6;②36
【分析】本题考查了全等三角形的判定与性质.熟练掌握全等三角形的判定条件是解题的关键.
(1)由题意知,,,则,证明;
(2)①由题意知,,由,可得,计算求解即可;②根据,计算求解即可.
【详解】(1)证明:∵,
∴,
∵,
∴,即,
∴,
∵,,,
∴;
(2)①解:∵点E是的中点,
∴,
由(1)可知,,
∴,
∴,
∴的长为6;
②解:由题意知,,
∴的面积为36.
【变式4-2】(23-24·四川达州·模拟预测)如图,在梯形中,,,于点E,,求证.
【答案】见解析
【分析】本题主要考查全等三角形的判定以及平行线的性质,熟练掌握全等三角形的判定是解题的关键.根据题意证明,根据即可得到答案.
【详解】证明:,
,
,
,
,
,
,
在和中,
,
.
【变式4-3】(23-24八年级·山西太原·阶段练习)如图,教学楼与操场上的旗杆相距,小林同学从教学楼点沿走到点,一定时间后他到达点,此时他测得和的夹角为,且,已知,旗杆的高为,小林同学行走的速度为.
(1)请你求出教学楼的高度;
(2)小林从点到达点还需要多长时间?
【答案】(1)
(2)
【分析】本题考查的是全等三角形的判定与性质,熟记全等三角形的判定方法是解本题的关键;
(1)先证明,再结合,即可得到结论;
(2)利用路程除以速度即可得到答案.
【详解】(1)解:∵和的夹角为,
∴.
∵,
∴,
∴.
在和中,
,
∴,
∴,.
∵,
∴.
∵,
∴,
∴.
答:教学楼的高度为.
(2).
答:小林从点到达点还需要.
【题型5 已知边为角的邻边找夹角的另一边,用SAS】
【例5】(23-24八年级·广东深圳·期末)如图,中,,以为边向右下方作,满足,点为上一点,连接,若,,,则 .
【答案】5
【分析】本题考查全等三角形的判定与性质,正确作出辅助线,构造全等三角形是解题的关键.
延长到E,使,连接,先证明,得到,,再证明,得到,即可由,进而即可求解.
【详解】解:延长到E,使,连接,如图,
∵,,,
∴,
∴,,
∴,
∵,
∴,
∴,
∴,
在与中,
,
∴,
∴,
∴.
故答案为:5.
【变式5-1】(23-24八年级·江苏苏州·期末)如图,在中,为中点,为边上一点,连接,并延长至点 ,使得,连接.
(1)求证:;
(2)若,,,求的度数.
【答案】(1)证明见解析;
(2).
【分析】()由为中点得,然后用“”证明即可;
()由,得, 三角形的内角和得,最后由平行线的性质即可求解;
本题考查了全等三角形的判定与性质,平行线的性质,三角形的内角和,熟练掌握知识点的应用是解题的关键.
【详解】(1)证明:∵为中点,
∴,
在和中,
,
∴;
(2)由()得:,
∴,
∵,,
∴,
∵,
∴.
【变式5-2】(23-24八年级·黑龙江哈尔滨·阶段练习)已知,,.
(1)如图1,求证:;
(2)如图2,与相交于点,若,,求的度数.
【答案】(1)证明见解析
(2)
【分析】
本题考查三角形全等的判定与性质、三角形外角性质及三角形内角和定理等知识,熟练掌握三角形全等的判定与性质是解决问题的关键.
(1)利用三角形全等判定与性质,证得,即可得证;
(2)利用全等三角形性质得到,再由三角形外角性质与三角形内角和定理数形结合即可得到答案.
【详解】(1)证明: ,,
,
在和中,
,
;
(2)解:由(1)知,,
在中,是其外角,则,
在中,.
【变式5-3】(23-24八年级·江西吉安·阶段练习)如图,某游乐园有两个滑梯与,滑梯的高与滑梯水平方向的长度相等,且的长度等于长方形周长的一半.
(1)两个滑梯与的长度是否相等?并说明理由.
(2)若,试说明.
【答案】(1)相等,理由见解析
(2)见解析
【分析】本题考查了全等三角形的应用;确定两角的大小关系,通常可证明这两角所在的三角形全等,根据对应角相等进行判定.
(1)根据的长度等于长方形周长的一半,得出,证明,即可证明;
(2)根据全等三角形的性质得出,结合,得出,证出,即可证明;
【详解】(1)解:.
理由:∵的长度等于长方形周长的一半,
∴,
∴.
在和中,
,
∴,
∴.
(2)∵,
∴.
∵,
∴,
∴.
∵,
∴,
∴.
【题型6 已知边为角的邻边找夹边的另一角,用ASA】
【例6】(23-24·四川达州·模拟预测)如图,在梯形中,,,于点E,,求证.
【答案】见解析
【分析】本题主要考查全等三角形的判定以及平行线的性质,熟练掌握全等三角形的判定是解题的关键.根据题意证明,根据即可得到答案.
【详解】证明:,
,
,
,
,
,
,
在和中,
,
.
【变式6-1】(23-24·吉林松原·模拟预测)如图,在中,是斜边上的高线,于点F,.求证:.
【答案】见解析
【分析】本题主要考查全等三角形的判定,熟练掌握全等三角形的判定是解题的关键.根据题意,利用证明即可.
【详解】证明:在中,.
,
.
.
,
.
在和中,
,
.
【变式6-2】(23-24八年级·浙江宁波·期末)如图, 是 的高线,与 相交于点 .若 ,且 的面积为12,则的长度为( )
A.1 B. C.2 D.3
【答案】C
【分析】本题主要考查了全等三角形的判定与性质,三角形的面积等知识,熟练掌握全等三角形的判定与性质是解题的关键.利用证明,得,再根据三角形面积可得的长,从而可得答案.
【详解】解:∵,是的高线,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵的面积为12,
∴,
∴,
∴,
∴,
故选:C.
【变式6-3】(23-24八年级·重庆大渡口·阶段练习)如图,在中,,,过点C作,连接.
(1)基本尺规作图:作,交线段于点F(保留作图疯迹);
(2)求证:.
解:∵,
∴________
∵
∴
在和中
∴,
∴(_______)
【答案】(1)见解析
(2)见解析
【分析】(1)根据运用作相等角的作图方法画图即可;
(2)根据平行线的性质可推出①及②,再根据全等三角形的判定定理和性质可得③④.
【详解】(1)解:如图:即为所求;
(2)解:∵
∴(两直线平行,同旁内角互补)
∵
∴
在和中
∴
∴(全等三角形的对应边相等).
【题型7 已知边为角的邻边找边的对角,用AAS】
【例7】(23-24八年级·湖北鄂州·期末)如图,中,是边上的中线,过C作,垂足为F,过B作交的延长线于D.
(1)求证:;
(2)若,求的长.
【答案】(1)见解析
(2)
【分析】(1)证两条线段相等,通常用全等,本题中的和分别在和中,在这两个三角形中,已经有一组边相等,一组角相等了,因此只需再找一组角即可利用角角边进行解答.
(2)由(1)得,且,即可求出的长.
【详解】(1)∵,
∴.
∴.
在和中,
∵
∴.
∴.
(2)∵,
∴,
∵是边上的中线,
∴,且.
∴.
【点睛】三角形全等的判定一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
【变式7-1】(23-24八年级·江西吉安·阶段练习)将两个三角形纸板和按如图所示的方式摆放,连接.已知,,.
(1)试说明.
(2)若,求的度数.
【答案】(1)见解析
(2)
【分析】(1)利用证明三角形全等即可;
(2)全等三角形的性质,得到,证明,得到,即可得解.
【详解】(1)解:因为,
所以,
即.
在和中,
,
所以.
(2)因为,
所以,.
在和中,
,
所以,
所以,
所以.
【点睛】本题考查全等三角形的判定和性质.解题的关键是证明三角形全等.
【变式7-2】(23-24八年级·四川宜宾·期中)已知:如图,在和中,.求证:
(1);
(2).
【答案】(1)见解析
(2)见解析
【分析】本题考查了三角形的全等判定和性质,熟练掌握判定定理是解题的关键.
(1)根据得到即,证明即可.
(2)根据得到,结合,得到即,证明即可.
【详解】(1)∵,
∴,
∴,
∵,
∴,
∴.
(2)∵
∴,
∵,
∴,
∴,
∵,
∴.
【变式7-3】(23-24·黑龙江哈尔滨·一模)如图,在四边形中,于点F,交BC于点G,交的延长线于点E,且.
(1)求证:;
(2)如图2,连接AG,若,请直接写出图2中的三角形,使写出的每个三角形的面积是面积的2倍.
【答案】(1)见详解
(2)
【分析】本题考查了全等三角形的判定与性质,以及共高三角形面积比等于底之比,熟练掌握基本知识是解题的关键;
(1)用即可证明;
(2)先证明,则,再证明,则,由与同底等高,得,再证明,则,最后与同底等高,
得,所以.
【详解】(1)证明:∵
∴
∴在和中,
,
∴;
(2)
∵
∴,
∵,
∴,
∴
∵,
∴
∵,
∴,
∴,
∴,
∵,
∴,
∴
∵ ,,
∴,
∴
∵
∴与同底等高,
∴,
∴
∵,∴,
∴,
∴,
∴,∵,
∴,
∴,
∵
∴与同底等高,
∴,
∴,
∴的面积为面积的2倍.
【题型8 已知两角找夹边,用ASA】
【例8】(23-24八年级·陕西西安·期末)如图,,平分,下列结论∶① 平分;②;③;④.其中正确的有( )
A.①③ B.③④ C.①③④ D.②③④
【答案】C
【分析】题目主要考查全等三角形的判定和性质,平行线的性质,理解题意,结合图形求解是解题关键.
根据平行线的性质及各角之间的等量代换得出,再由角平分线及等量代换可判断①;根据全等三角形的判定和性质可判断②和④;利用三角形面积的关系可判断③,即可得出结果.
【详解】解:∵ ,
∴
,
∵ 平分,
,
∴ 平分,故①正确;
在上截取,连接,
在和中,
∴
,
在和中,
,,
故②不正确,④正确;
,
∴,
故③正确;
故选:C.
【变式8-1】(23-24八年级·云南昭通·期末)如图,C,F为线段BE上两点,,,.求证:.
【答案】见解析
【分析】本题考查全等三角形的判定和性质,先由证明,再证,即可证明 ,由此可得.
【详解】证明: ,
,
,
,即,
在和中,
,
,
.
【变式8-2】(23-24八年级·辽宁阜新·期末)如图,于点,于点,与交于点,且,.求证:.
【答案】证明见解析
【分析】本题主要考查了全等三角形的性质与判定,先利用证明得到,进而利用证明,即可证明.
【详解】证明:,,
.
,
,即,
又∵,即
,
∴,
在与中,
,
,
.
【变式8-3】(23-24八年级·黑龙江哈尔滨·期末)在 中, 和 的平分线相交于点 F.
(1)如图1,连接,求证:
(2)如图2,当时,若,求的长.
【答案】(1)见解析
(2)7
【分析】本题主要考查了角平分线的性质,三角形内角和定理,全等三角形的判定和性质:
(1)在中,根据三角形内角和定理可得,再由角平分线的定义可得,从而得到,即可解答;
(2)连接,在上截取,连接,由(1)得:,从而得到,,再证明,可得,从而得到,可证明,从而得到,即可求解.
【详解】(1)证明:在中, ,
∵和 的平分线相交于点 F.
∴,,
∴,
∴,
∴,
∴;
(2)解:如图,连接,在上截取,连接,
由(1)得:,
∵,
∴,
∴,
∴,
∵平分,
∴,
∵,,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴.
【题型9 已知两角找任一角的对边,用AAS】
【例9】(23-24八年级·福建三明·期中)如图,在中,,将沿射线的方向平移至,连接,设与的交点为.
(1)若为的中点,求证:;
(2)若平分,求的度数.
【答案】(1)见解析
(2)
【分析】本题主要考查几何变换,平移的性质,全等三角形的判定和性质,等腰三角形的性质,掌握和理解这些性质进行推理是解题的关键.
(1)根据平移性质得到,,从而得到,再根据为的中点,得到,从而证明结论;
(2)根据平分,得到,从而证明.再根据三角形内角和定理以及,即可求解;
【详解】(1)解:由沿射线的方向平移所得,
,,
,
为的中点,
,
.
在和中
,
;
(2)平分,
,
又,
.
,,
.
【变式9-1】(23-24·陕西西安·三模)如图,点B,F,C,E在一条直线上,点A,D在这条直线的两侧,已知,,.求证:.
【答案】见解析
【分析】此题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键:先推出,由此证得,得到,即可推出.
【详解】证明:∵,
∴,
∴,
在和中,
∴,
∴,
∴.
【变式9-2】(23-24八年级·浙江金华·阶段练习)如图,在和中,点在同一直线上,,.
(1)求证:;
(2)当时,求的度数.
【答案】(1)证明见解析;
(2).
【分析】()由可得,利用即可证明;
(),可得,即可求解;
本题考查了全等三角形的判定和性质,三角形内角和定理,掌握全等三角形的判定和性质是解题的关键.
【详解】(1)证明:∵,
∴,
即,
在和中,
,
∴;
(2)解:∵,,
∴,
∵
∴.
【变式9-3】(23-24八年级·山东青岛·期末)已知,在中,,.在内部作,交于点D.将一个含有45°角的三角板如图放置,使直角边与重合,三角板沿平移.
(1)如图1,当三角板的另一条直角边过点A时,试证明;
(2)将三角板沿平移至图2的位置,与交于点M,过点M作,垂足为点N,试判断线段之间的关系.
【答案】(1)见解析
(2)
【分析】(1)根据等腰三角形的性质得到,根据全等三角形的性质即可得到结论;
(2)过A作于P,于Q,则四边形是矩形,根据矩形的性质得到,,根据平行线的性质得到,得到,由(1)知,,等量代换得到,于是得到结论.
【详解】(1)证明:∵,
∴,
在与中,
,
∴,
∴;
(2).
理由:过A作于P,于Q,
则四边形是长方形
,,
∴,
∵,
∴,
∵,
∴,
由(1)知,,
∴,
∵,
∴.
【点睛】本题考查了作图一平移变换,全等三角形的判定和性质,等腰三角形的性质,矩形的判定和性质,正确地作出辅助线是解题的关键.
21世纪教育网(www.21cnjy.com)
