人教版2024-2025学年八年级数学上册举一反三专题12.2三角形全等的判定(基础篇)【十大题型】(学生版+解析)
文档属性
| 名称 | 人教版2024-2025学年八年级数学上册举一反三专题12.2三角形全等的判定(基础篇)【十大题型】(学生版+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 13:10:31 | ||
图片预览



文档简介
专题12.2 三角形全等的判定(基础篇)【十大题型】
【人教版】
【题型1 利用SSS证明三角形全等】 1
【题型2 SSS与全等三角形的性质综合应用】 2
【题型3 利用SAS证明三角形全等】 4
【题型4 SAS与全等三角形的性质综合应用】 5
【题型5 利用ASA证明三角形全等】 6
【题型6 ASA与全等三角形的性质综合应用】 7
【题型7 利用AAS证明三角形全等】 9
【题型8 AAS与全等三角形的性质综合应用】 10
【题型9 利用HL证明三角形全等】 11
【题型10 HL与全等三角形的性质综合应用】 12
知识点1:由边边边(SSS)证明两个三角形全等
三边分别相等的两个三角形全等,简写成“边边边”或“SSS”.
当三角形的三边确定后,其形状、大小也随之确定.这也是三角形具有稳定性的原因.
【题型1 利用SSS证明三角形全等】
【例1】(23-24八年级·山西晋中·期末)如图是某款雨伞的实物图,图是该雨伞部分骨架示意图.测得,点,分别是,的三等分点,,那么的依据是( )
A. B. C. D.
【变式1-1】(23-24八年级·全国·课后作业)如图所示,,,用三角形全等的判定“SSS”可证明 或 .
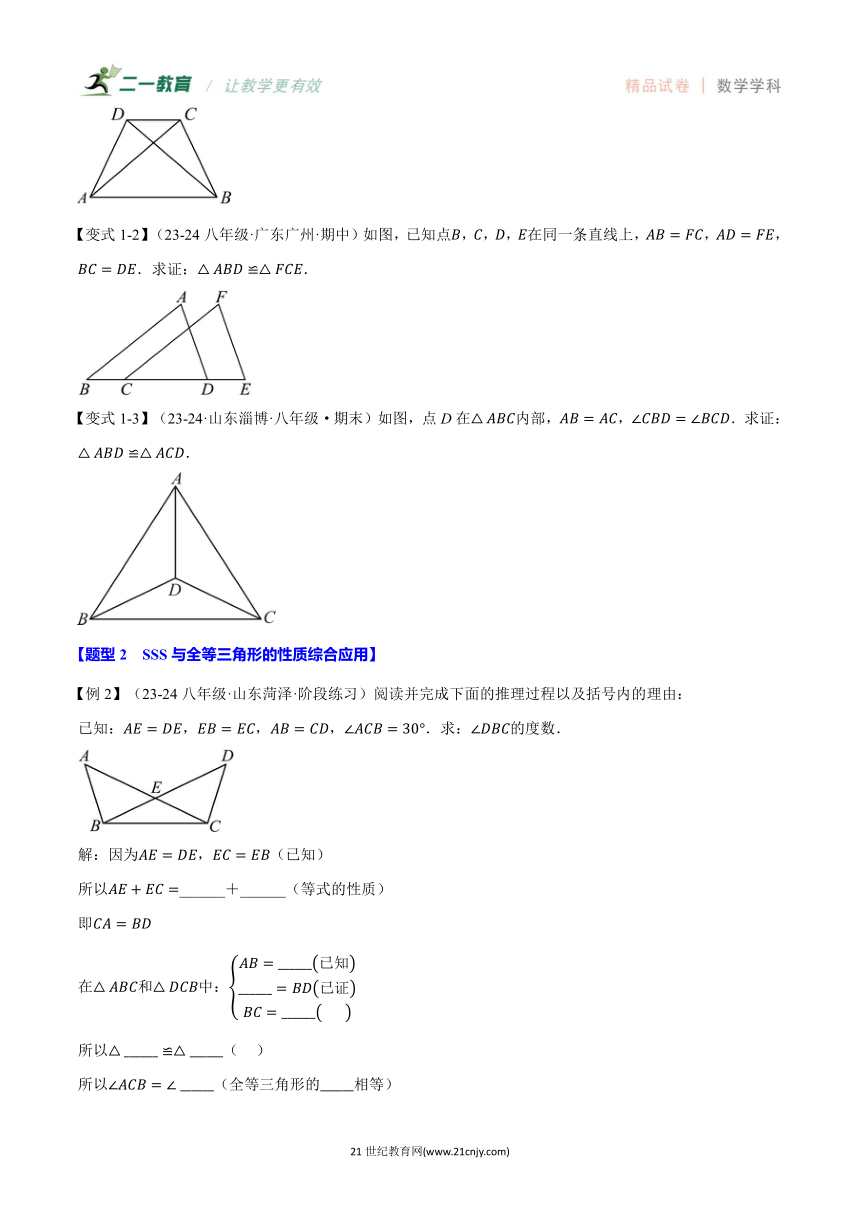
【变式1-2】(23-24八年级·广东广州·期中)如图,已知点,,,在同一条直线上,,,.求证:.
【变式1-3】(23-24·山东淄博·八年级·期末)如图,点D在内部,,.求证:.
【题型2 SSS与全等三角形的性质综合应用】
【例2】(23-24八年级·山东菏泽·阶段练习)阅读并完成下面的推理过程以及括号内的理由:
已知:,,,.求:的度数.
解:因为,(已知)
所以______+______(等式的性质)
即
在和中:
所以( )
所以 (全等三角形的相等)
因为
所以 .
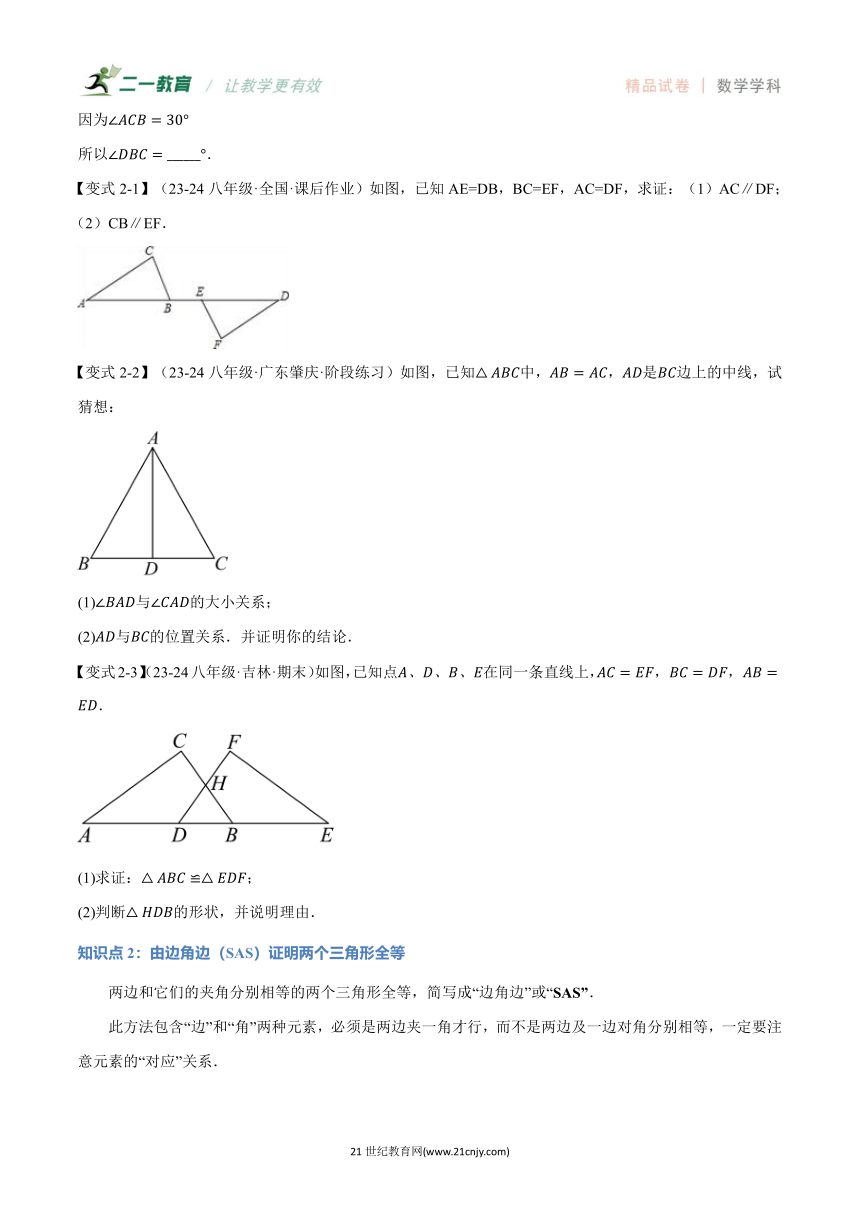
【变式2-1】(23-24八年级·全国·课后作业)如图,已知AE=DB,BC=EF,AC=DF,求证:(1)AC∥DF;(2)CB∥EF.
【变式2-2】(23-24八年级·广东肇庆·阶段练习)如图,已知中,,是边上的中线,试猜想:
(1)与的大小关系;
(2)与的位置关系.并证明你的结论.
【变式2-3】(23-24八年级·吉林·期末)如图,已知点在同一条直线上,.
(1)求证:;
(2)判断的形状,并说明理由.
知识点2:由边角边(SAS)证明两个三角形全等
两边和它们的夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.
此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.
【注意】(1)此方法是证明两个三角形全等最常用的方法之一,应用时,可以从图形上直接观察到三个对应元素必须符合“两边夹角”,即“SAS”,不要误认为有两边一角就能判定两个三角形全等.
(2)在书写时也要按照“边→角→边”的顺序排列条件,必须牢记“边边角”不能作为判定两个三角形全等的条件.
【题型3 利用SAS证明三角形全等】
【例3】(23-24八年级·河南郑州·期末)如图,小明要测量水池的宽,但没有足够长的绳子,聪明的他想了如下办法:先在地上取一个可以直接到达点和点的点,连接并延长到,使,连接并延长到,使,连接并测量出它的长度,则的长度就是的长,理由是根据 (用简写形式即可),可以得到,从而由全等三角形的对应边相等得出结论.
【变式3-1】(23-24八年级·江苏宿迁·阶段练习)如图,点、在上,,要用证,则需添加的条件为 .
【变式3-2】(23-24·云南昆明·八年级·期末)如图,,.求证:.
【变式3-3】(23-24八年级·陕西咸阳·期中)如图,等边中,是的角平分线,为上一点,以为一边且在下方作等边,连接,求证:.
【题型4 SAS与全等三角形的性质综合应用】
【例4】(23-24·陕西·模拟预测)如图,在中,,过点作,且,求证:.
【变式4-1】(23-24八年级·上海·专题练习)如图,在中,已知点、、分别在边、、上,且,,,那么和的大小关系如何?为什么?
解:因为 ,
即.
又因为(已知),
所以 .
在和中,
所以 .
因此.
【变式4-2】(23-24八年级·内蒙古通辽·期中)如图,在中,,,过点作,垂足为,延长至.使得.在边上截取,连结.
(1)求∠的度数.
(2)求证:.
【变式4-3】(23-24八年级·河南郑州·期末)如图,四边形、都是正方形,连接、.求证:
(1);
(2).
知识点3:由角边角(ASA)证明两个三角形全等
两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
用“ASA”来判定两个三角形全等,一定要证明这两个三角形有两个角以及这两个角的夹边分别相等,证明时要加强对夹边的认识.
【题型5 利用ASA证明三角形全等】
【例5】(23-24八年级·河南郑州·期末)如图,为的中点,点为射线上(不与点重合)的任意一点,连接,并使的延长线交射线于点.试说明:.
【变式5-1】(23-24八年级·湖北武汉·期中)一块三角形玻璃被摔成如图所示的四块,小江想去买一块形状、大小与原来一样的玻璃,但是他只想带去其中的两块,则这两块玻璃的编号可以是( )
A.①② B.②④ C.③④ D.①④
【变式5-2】(23-24八年级·山东枣庄·阶段练习)如图,、、、在同一条直线上,,,,试说明:.
【变式5-3】(23-24八年级·河南郑州·期末)已知:点B、E、C、F在一条直线上,.求证:.
【题型6 ASA与全等三角形的性质综合应用】
【例6】(23-24八年级·云南昭通·阶段练习)如图,,,,,则等于 .
【变式6-1】(23-24八年级·重庆·期末)如图,某段河流的两岸是平行的,小开想出了一个不用涉水过河就能测得河的宽度的方案,首先在岸边点B处,选对岸正对的一棵树A,然后沿河岸直行到达树C,继续前行到达点D处,再从点D处沿河岸垂直的方向行走.当到达树A正好被树C遮挡住的点E处时,停止行走,此时的长度即为河岸的宽度.小开这样判断的依据是( )
A. B. C. D.
【变式6-2】(23-24八年级·浙江·期末)如图,在和中,点在边上,,,.
(1)求证:.
(2)若,求的度数.
【变式6-3】(23-24八年级·广东佛山·阶段练习)如图,已知,的平分线恰好交于上一点,已知,,则 .
知识点4:由角角边(AAS)证明两个三角形全等
两角和其中一个角的对边分别相等的两个三角形全等,简写成“角角边”或“AAS”.这一结论很容易由“ASA”推得,将这一结论与“ASA”结合起来,即可得出:两个三角形如果具备两角和一条边对应相等,就可判定其全等.
【题型7 利用AAS证明三角形全等】
【例7】(23-24·陕西西安·八年级·期末)如图,点在上,,,.求证:
【变式7-1】(23-24八年级·山西太原·阶段练习)如图,太阳光线和是平行的,在同一时刻,两根高度相等的木杆的影子是一样长的,这利用了全等图形的性质,其中判断的依据是 .
【变式7-2】(23-24·山东淄博·八年级·期末)如图, 点在的外部,点在上,交于点, ,.求证: .
【变式7-3】(23-24八年级·安徽合肥期末)如图,在四边形中,点在边上,.求证:.
【题型8 AAS与全等三角形的性质综合应用】
【例8】(23-24八年级·河南周口·期中)如图,在中,是边上的高,是边上的高,且交于点F,若,则线段的长为 .
【变式8-1】(23-24八年级·重庆·期末)在中,,过点A作于点D,延长至点E,使得,过点E作,交的延长线于点F,连接.
(1)求证:;
(2)若,,求的度数.
【变式8-2】(23-24八年级·上海普陀·期末)如图,已知,,.试说明的理由.
解:因为(已知),
所以(垂直的意义).
同理 .
所以(等量代换).
在和中,
所以( ).
得 (全等三角形的对应边相等).
又因为(已知),
所以( ).
【变式8-3】(23-24八年级·陕西西安·阶段练习)如图所示,工人赵师傅用10块高度都是的相同长方体新型建筑材料,垒了两堵与地面垂直的墙和,其中于点B,于点E,点P在上,已知,.
(1)求证:;
(2)求的长.
知识点5:由斜边、直角边(HL)证明两个三角形全等
斜边和一条直角边分别相等的两个直角三角形全等,简写成“斜边、直角边”或“HL”.
“HL”定理是直角三角形所独有的,对于一般三角形不成立.
【题型9 利用HL证明三角形全等】
【例9】(23-24八年级·陕西西安·期末)如图,在和中,点B、D、C、E在同一条直线上,点C和点E重合.,,若添加一个条件后可用“”定理证明,添加的条件是( )
A. B. C. D.
【变式9-1】(23-24八年级·陕西榆林·期中)如图,在四边形中,,,是上一点,且,连接、,.求证:.
【变式9-2】(23-24八年级·云南保山·期末)用三角尺可按下面方法画角平分线:如图摆放使得三角板刻度相同,即,画射线,则平分.作图过程用了,那么所用的判定定理是( )
A. B. C. D.
【变式9-3】(23-24八年级·山东济南·期末)如图,在和中,,,与分别为,边上的中线,且,求证:.
【题型10 HL与全等三角形的性质综合应用】
【例10】(23-24八年级·广西贵港·期末)小强在物理课上学习了发声物体的振动试验后,对其作了进一步的探究:在一个支架的横杆点处用一根细绳悬挂一个小球,小球可以自由摆动,如图,A表示小球静止时的位置,当小强用发声物体靠近小球时,小球从A摆到位置,此时过点作于点,当小球摆到位置时,过点作于点,测得(图中的点在同一平面内).
(1)猜想此时与的位置关系,并说明理由;
(2)求的长.
【变式10-1】(23-24八年级·辽宁大连·期末)一天数学课堂上,小明忘记了带圆规,于是他尝试用直角三角板来画角平分线.如图,在的两边上,分别取,将两个直角三角板的直角顶点放在点,处作,的垂线,交点为,一个三角板的斜边与另一个三角板直角边交于点,画射线 就得到的平分线.
【变式10-2】(23-24八年级·江苏盐城·期末)已知:如图,,.求证:.
【变式10-3】(23-24八年级·陕西西安·期中)如图,已知是的高,E为上一点,交于点F,且,求的度数.
21世纪教育网(www.21cnjy.com)
专题12.2 三角形全等的判定(基础篇)【十大题型】
【人教版】
【题型1 利用SSS证明三角形全等】 1
【题型2 SSS与全等三角形的性质综合应用】 4
【题型3 利用SAS证明三角形全等】 8
【题型4 SAS与全等三角形的性质综合应用】 10
【题型5 利用ASA证明三角形全等】 14
【题型6 ASA与全等三角形的性质综合应用】 17
【题型7 利用AAS证明三角形全等】 20
【题型8 AAS与全等三角形的性质综合应用】 23
【题型9 利用HL证明三角形全等】 27
【题型10 HL与全等三角形的性质综合应用】 29
知识点1:由边边边(SSS)证明两个三角形全等
三边分别相等的两个三角形全等,简写成“边边边”或“SSS”.
当三角形的三边确定后,其形状、大小也随之确定.这也是三角形具有稳定性的原因.
【题型1 利用SSS证明三角形全等】
【例1】(23-24八年级·山西晋中·期末)如图是某款雨伞的实物图,图是该雨伞部分骨架示意图.测得,点,分别是,的三等分点,,那么的依据是( )
A. B. C. D.
【答案】D
【分析】本题考查全等三角形的应用,由点,分别是,的三等分点,,得出,根据三边对应相等,证明.解题的关键是熟练掌握全等三角形的判定定理.
【详解】解:∵点,分别是,的三等分点,
∴,,
∵,
∴,
在与中,
,
∴.
故选:D.
【变式1-1】(23-24八年级·全国·课后作业)如图所示,,,用三角形全等的判定“SSS”可证明 或 .
【答案】
【分析】由、、可证出;由、、可证出.综上即可得出结论.
【详解】解:在和中,
,
∴;
在和中,
,
∴.
故答案为:;.
【点睛】本题主要考查全等三角形的判定,熟练掌握全等三角形的判定条件是解题的关键.
【变式1-2】(23-24八年级·广东广州·期中)如图,已知点,,,在同一条直线上,,,.求证:.
【答案】证明见解析.
【分析】本题考查了三角形全等的判定,由,则,即,再根据即可证明,掌握证明三角形全等的判定定理是解题得关键.
【详解】证明:∵,
∴,
即,
在和中,
,
∴.
【变式1-3】(23-24·山东淄博·八年级·期末)如图,点D在内部,,.求证:.
【答案】见解析
【分析】本题考查全等三角形的判定、等腰三角形的判定,由,可知,再利用即可证明结论,熟练掌握全等三角形的判定是解答的关键.
【详解】证明:∵,
∴,
在与中,
,
∴.
【题型2 SSS与全等三角形的性质综合应用】
【例2】(23-24八年级·山东菏泽·阶段练习)阅读并完成下面的推理过程以及括号内的理由:
已知:,,,.求:的度数.
解:因为,(已知)
所以______+______(等式的性质)
即
在和中:
所以( )
所以 (全等三角形的相等)
因为
所以 .
【答案】;;对应角;
【分析】本题考查了全等三角形的判定与性质,主要考查了学生的逻辑推理能力,解题的关键是熟练掌握全等三角形的判定方法;
根据,,得出,再利用证明 ,即可得出结论.
【详解】解:因为,(已知)
所以(等式的性质)
即
在和中:
所以
所以(全等三角形的对应角相等)
因为所以.
故答案为:;;;;;;;;对应角;.
【变式2-1】(23-24八年级·全国·课后作业)如图,已知AE=DB,BC=EF,AC=DF,求证:(1)AC∥DF;(2)CB∥EF.
【答案】(1)证明见解析(2)证明见解析
【详解】试题分析:(1)由SSS证明△ABC≌△DEF,得出对应角相等∠A=∠D,∠ABC=∠DEF,由内错角相等即可得出结论;
(2)由(1)得:∠ABC=∠DEF,得出∠CBE=∠FEB,由内错角相等即可得出结论.
试题解析:(1)∵AE=DB,
∴AE-BE=DB-BE,
即AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠A=∠D,∠ABC=∠DEF,
∴AC∥DF;
(2)由(1)得:∠ABC=∠DEF,
∴∠CBE=∠FEB,
∴CB∥EF.
【变式2-2】(23-24八年级·广东肇庆·阶段练习)如图,已知中,,是边上的中线,试猜想:
(1)与的大小关系;
(2)与的位置关系.并证明你的结论.
【答案】(1)
(2),证明见解析
【分析】(1)本题考查三角形中线的性质和三角形全等的判定与性质,灵活利用三角形全等判定,即可解题.
(2)本题考查利用三角形全等的性质,再结合邻补角互补即可证明该题.
【详解】(1)解:,理由如下:
是边上的中线,
,
在与中,
,
.
(2),理由如下:
证明:(已证),
,
,
,
.
【变式2-3】(23-24八年级·吉林·期末)如图,已知点在同一条直线上,.
(1)求证:;
(2)判断的形状,并说明理由.
【答案】(1)详见解析
(2)是等腰三角形
【分析】本题考查了全等三角形的判定和性质,等腰三角形的判定等知识.
(1)根据即可证明;
(2)由(1)可知,即可得到,即可得出结论.
【详解】(1)证明:在与中,
,
;
(2)解:是等腰三角形.理由:
,
,
,
即是等腰三角形.
知识点2:由边角边(SAS)证明两个三角形全等
两边和它们的夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.
此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.
【注意】(1)此方法是证明两个三角形全等最常用的方法之一,应用时,可以从图形上直接观察到三个对应元素必须符合“两边夹角”,即“SAS”,不要误认为有两边一角就能判定两个三角形全等.
(2)在书写时也要按照“边→角→边”的顺序排列条件,必须牢记“边边角”不能作为判定两个三角形全等的条件.
【题型3 利用SAS证明三角形全等】
【例3】(23-24八年级·河南郑州·期末)如图,小明要测量水池的宽,但没有足够长的绳子,聪明的他想了如下办法:先在地上取一个可以直接到达点和点的点,连接并延长到,使,连接并延长到,使,连接并测量出它的长度,则的长度就是的长,理由是根据 (用简写形式即可),可以得到,从而由全等三角形的对应边相等得出结论.
【答案】(或边角边)
【分析】本题考查了全等三角形的判定,根据题意知,,,可用证明两三角形全等.
【详解】由题意知,,
在和中,
,
.
故答案为:.
【变式3-1】(23-24八年级·江苏宿迁·阶段练习)如图,点、在上,,要用证,则需添加的条件为 .
【答案】/
【分析】本题考查了全等三角形的判定,根据且证,则添加条件为,即可作答.
【详解】解:∵运用证,且
∴添加条件为
即和中
∴
故答案为:
【变式3-2】(23-24·云南昆明·八年级·期末)如图,,.求证:.
【答案】见解析
【分析】本题考查了全等三角形的判定,根据直接证明两三角形全等,即可得证.
【详解】证明:在和中,
∵,
∴
【变式3-3】(23-24八年级·陕西咸阳·期中)如图,等边中,是的角平分线,为上一点,以为一边且在下方作等边,连接,求证:.
【答案】见解析
【分析】本题考查了等边三角形的性质、三角形全等的判定.先根据等边三角形的性质可得,,,从而可得,,再利用即可得证.
【详解】证明:,均为等边三角形,
,,
,
,即,
在和中,,
【题型4 SAS与全等三角形的性质综合应用】
【例4】(23-24·陕西·模拟预测)如图,在中,,过点作,且,求证:.
【答案】见解析
【分析】此题考查了全等三角形的判定与性质,熟练运用全等三角形的判定与性质是解题的关键.
根据等腰三角形的性质、平行线的性质求出,利用证明,根据“全等三角形的对应边相等”即可得证.
【详解】证明:∵,
∴,
∵,
∴,,
∴,
在和中,
,
∴,
∴,
即.
【变式4-1】(23-24八年级·上海·专题练习)如图,在中,已知点、、分别在边、、上,且,,,那么和的大小关系如何?为什么?
解:因为 ,
即.
又因为(已知),
所以 .
在和中,
所以 .
因此.
【答案】见解析
【分析】本题考查了全等三角形的判定和性质,三角形外角的性质,熟练掌握判定定理与性质定理,理清证明思路是写出理由与步骤的关键.
根据三角形外角的性质可得,再根据,证明,然后证明,得到.
【详解】解:因为(三角形的一个外角等于与它不相邻的两个内角的和),
即.
又因为(已知),
所以.
,
在和中,
所以.
因此.
【变式4-2】(23-24八年级·内蒙古通辽·期中)如图,在中,,,过点作,垂足为,延长至.使得.在边上截取,连结.
(1)求∠的度数.
(2)求证:.
【答案】(1)115°
(2)见解析
【分析】此题考查的是全等三角形的判定与性质;
(1)根据得出,进而根据三角形外角的性质可得出答案;
(2)证明,根据全等三角形的性质即可得出.
【详解】(1)解:.
.
,
;
(2)证明:在中,,,
.
.
在和中,
,
,
.
【变式4-3】(23-24八年级·河南郑州·期末)如图,四边形、都是正方形,连接、.求证:
(1);
(2).
【答案】(1)见解析
(2)见解析
【分析】本题主要考查了正方形的性质,三角形全等的判定和性质,三角形内角和定理的应用,解题的关键是根据三角形全等的判定方法,证明.
(1)利用正方形的性质得,,再利用得,即可证明;
(2)由(1)知,再结合条件证得,即.
【详解】(1)证明:∵四边形、都是正方形,
∴,,
∵,,
∴,
在和中,
,
∴,
∴;
(2)解:设与相交于点,与相交于点,
∵,
∴,
又∵,
∴,
∴.
知识点3:由角边角(ASA)证明两个三角形全等
两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
用“ASA”来判定两个三角形全等,一定要证明这两个三角形有两个角以及这两个角的夹边分别相等,证明时要加强对夹边的认识.
【题型5 利用ASA证明三角形全等】
【例5】(23-24八年级·河南郑州·期末)如图,为的中点,点为射线上(不与点重合)的任意一点,连接,并使的延长线交射线于点.试说明:.
【答案】见解析
【分析】本题主要考查了利用证明三角形全等,由P为的中点,可得,再由对顶角相等可得出,结合已知条件可得出.
【详解】解为的中点,
.
又 ,
【变式5-1】(23-24八年级·湖北武汉·期中)一块三角形玻璃被摔成如图所示的四块,小江想去买一块形状、大小与原来一样的玻璃,但是他只想带去其中的两块,则这两块玻璃的编号可以是( )
A.①② B.②④ C.③④ D.①④
【答案】A
【分析】本题考查了全等三角形的应用,学会把实际问题转化为数学问题是解答的关键.
①②两块玻璃是已知两角及其一夹边,可用证明全等来说理.
【详解】解:A、①②两块玻璃是已知两角及其一夹边,可用证明全等,故本选项符合题意;
B、②④两块玻璃是已知两角,无法证明全等,故本选项不符合题意;
C、③④两块玻璃是已知一角,无法证明全等,故本选项不符合题意;
D、①④两块玻璃是已知两角,无法证明全等,故本选项不符合题意.
故选:A.
【变式5-2】(23-24八年级·山东枣庄·阶段练习)如图,、、、在同一条直线上,,,,试说明:.
【答案】见解析
【分析】本题主要考查了全等三角形的判定,先证明,再利用证明即可证明结论.
【详解】解:,
,即,
在和中,
,
) .
【变式5-3】(23-24八年级·河南郑州·期末)已知:点B、E、C、F在一条直线上,.求证:.
【答案】见解析
【分析】此题考查了全等三角形的判定,由平行线的性质得到,,由线段之间的关系得到,即可证明.
【详解】证明:∵,
∴,
∵,
∴,
∵,
∴,
即,
在和中,
,
∴.
【题型6 ASA与全等三角形的性质综合应用】
【例6】(23-24八年级·云南昭通·阶段练习)如图,,,,,则等于 .
【答案】3;
【分析】本题考查三角形全等的判定及性质,根据得到,结合角边角判定即可得到答案;
【详解】解:∵,
∴,
在与中,
∵,
∴,
∴,
∵,,
∴,
故答案为:3.
【变式6-1】(23-24八年级·重庆·期末)如图,某段河流的两岸是平行的,小开想出了一个不用涉水过河就能测得河的宽度的方案,首先在岸边点B处,选对岸正对的一棵树A,然后沿河岸直行到达树C,继续前行到达点D处,再从点D处沿河岸垂直的方向行走.当到达树A正好被树C遮挡住的点E处时,停止行走,此时的长度即为河岸的宽度.小开这样判断的依据是( )
A. B. C. D.
【答案】D
【分析】本题主要考查了全等三角形的判定和性质,解题的关键是熟练掌握三角形全等的判定方法,,,,,.根据,,再根据对顶角相等,利用证明即可.
【详解】解:由题意,得,,
在与中,
∴,
∴,
∴小开这样判断的依据是.
故选:D.
【变式6-2】(23-24八年级·浙江·期末)如图,在和中,点在边上,,,.
(1)求证:.
(2)若,求的度数.
【答案】(1)见详解
(2)
【分析】本题主要考查了全等三角形的判定与性质、等腰三角形的判定与性质等知识,利用“”证明是解题关键.
(1)首先证明,然后利用“”证明即可;
(2)首先根据全等三角形的性质可得,,再结合等腰三角形“等边对等角”的性质可得,然后由求解即可.
【详解】(1)证明:∵,
∴,
∴,
在和中,
,
∴;
(2)∵,,
∴,,
∴,
∴.
【变式6-3】(23-24八年级·广东佛山·阶段练习)如图,已知,的平分线恰好交于上一点,已知,,则 .
【答案】7
【分析】本题考查的是全等三角形的判定和性质、等腰三角形的性质,掌握全等三角形的判定定理和性质定理是解题的关键.延长交的延长线于点,根据等腰三角形的性质得到,利用定理证明,根据全等三角形的性质得到,进而求出.
【详解】解:延长交的延长线于点,
平分,
,
,
,
,
,
平分,
,
在和中,
,
,
,
,
故答案为:7.
知识点4:由角角边(AAS)证明两个三角形全等
两角和其中一个角的对边分别相等的两个三角形全等,简写成“角角边”或“AAS”.这一结论很容易由“ASA”推得,将这一结论与“ASA”结合起来,即可得出:两个三角形如果具备两角和一条边对应相等,就可判定其全等.
【题型7 利用AAS证明三角形全等】
【例7】(23-24·陕西西安·八年级·期末)如图,点在上,,,.求证:
【答案】见详解
【分析】先根据平行线的性质得到,然后根据“”可判断.本题考查了全等三角形的判定:熟练掌握全等三角形的5种判定方法是解决问题的关键.选用哪一种方法,取决于题目中的已知条件.
【详解】解:,
,
在和中,
,
.
【变式7-1】(23-24八年级·山西太原·阶段练习)如图,太阳光线和是平行的,在同一时刻,两根高度相等的木杆的影子是一样长的,这利用了全等图形的性质,其中判断的依据是 .
【答案】
【分析】此题考查全等三角形的应用,解题关键是掌握全等三角形的判定方法.
根据平行线的性质可得,根据题意可得,,然后利用判定.
【详解】解: ,
,
两根高度相同的木杆竖直插在地面上,
∴,,
在和中,
,
∴.
故答案为:.
【变式7-2】(23-24·山东淄博·八年级·期末)如图, 点在的外部,点在上,交于点, ,.求证: .
【答案】见解析
【分析】本题考查了全等三角形的判定,三角形内角和,熟知判定方法是解题的关键.通过,,可得,即可通过证明.
【详解】证明:,
,即,
,
,
即,
在与中,
.
【变式7-3】(23-24八年级·安徽合肥期末)如图,在四边形中,点在边上,.求证:.
【答案】见解析
【分析】
本题考查了全等三角形的判定.利用等角的余角相等求得和,再利用即可证明.
【详解】证明:∵,
∴,
∵,
∴,
∵,
∴.
【题型8 AAS与全等三角形的性质综合应用】
【例8】(23-24八年级·河南周口·期中)如图,在中,是边上的高,是边上的高,且交于点F,若,则线段的长为 .
【答案】6
【分析】本题主要考查了全等三角形的判定与性质,利用证明,得,,即可得出答案.
【详解】解:是边上的高,是边上的高,
,
,
,
在和中,
,
,
,
.
故答案为:6.
【变式8-1】(23-24八年级·重庆·期末)在中,,过点A作于点D,延长至点E,使得,过点E作,交的延长线于点F,连接.
(1)求证:;
(2)若,,求的度数.
【答案】(1)见解析
(2)
【分析】本题主要考查了三角形全等的判定,平行线的性质,三角形内角和定理的应用,解题的关键是数形结合,熟练掌握三角形全等的判定方法.
(1)根据“”证明即可;
(2)根据三角形内角和定理得出,根据,求出即可.
【详解】(1)证明:∵,
∴,
∵,,
∴,
∵,
∴.
(2)解:∵,,
∴,
∴,
∴.
【变式8-2】(23-24八年级·上海普陀·期末)如图,已知,,.试说明的理由.
解:因为(已知),
所以(垂直的意义).
同理 .
所以(等量代换).
在和中,
所以( ).
得 (全等三角形的对应边相等).
又因为(已知),
所以( ).
【答案】见详解
【分析】本题主要考查了全等三角形的判定以及性质,等腰三角形三线合一的性质,垂线的意义,根据垂线得意义可得出,再利用证明,根据全等三角形的性质可得出,再根据等腰三角形三线合一的性质即可证明.
【详解】解:因为(已知),
所以(垂直的意义).
同理.
所以(等量代换).
在和中,
所以().
得(全等三角形的对应边相等).
又因为(已知),
所以(等腰三角形三线合一性质)
【变式8-3】(23-24八年级·陕西西安·阶段练习)如图所示,工人赵师傅用10块高度都是的相同长方体新型建筑材料,垒了两堵与地面垂直的墙和,其中于点B,于点E,点P在上,已知,.
(1)求证:;
(2)求的长.
【答案】(1)见解析
(2)的长为
【分析】题目主要考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题关键.
(1)根据垂直及各角之间的等量代换得出,再由全等三角形的判定即可证明;
(2)由题意得:,,再由全等三角形的性质结合图形求解即可.
【详解】(1)证明:由题意得:,
∴.
∴.
∵,
∴.
∴
在和中
,
∴;
(2)解:由题意得:,,
由(1)得,
∴,.
∴.
答:的长为.
知识点5:由斜边、直角边(HL)证明两个三角形全等
斜边和一条直角边分别相等的两个直角三角形全等,简写成“斜边、直角边”或“HL”.
“HL”定理是直角三角形所独有的,对于一般三角形不成立.
【题型9 利用HL证明三角形全等】
【例9】(23-24八年级·陕西西安·期末)如图,在和中,点B、D、C、E在同一条直线上,点C和点E重合.,,若添加一个条件后可用“”定理证明,添加的条件是( )
A. B. C. D.
【答案】D
【分析】本题考查了全等三角形的判定.熟练掌握全等三角形的判定是解题的关键.根据进行判断作答即可.
【详解】解:由题意知,添加的条件为,
∵,,
∴,
故选:D.
【变式9-1】(23-24八年级·陕西榆林·期中)如图,在四边形中,,,是上一点,且,连接、,.求证:.
【答案】证明见解析
【分析】本题主要考查了全等三角形的判定,平行线的性质,等角对等边,先由平行线的性质求出,再由等角对等边得到,据此利用即可证明.
【详解】证明:∵,
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴.
【变式9-2】(23-24八年级·云南保山·期末)用三角尺可按下面方法画角平分线:如图摆放使得三角板刻度相同,即,画射线,则平分.作图过程用了,那么所用的判定定理是( )
A. B. C. D.
【答案】C
【分析】本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判断和性质是解题的关键.根据已知条件得出得出答案.
【详解】解:∵,,
∴,
在和中,
,
∴.
故选:C.
【变式9-3】(23-24八年级·山东济南·期末)如图,在和中,,,与分别为,边上的中线,且,求证:.
【答案】见解析
【分析】此题考查了全等三角形的判定,根据三角形中线的定义得到,,由,得到,利用即可证明.
【详解】证明:∵与分别为,边上的中线,
∴,,
∵,
∴,
在和中,
,
∴.
【题型10 HL与全等三角形的性质综合应用】
【例10】(23-24八年级·广西贵港·期末)小强在物理课上学习了发声物体的振动试验后,对其作了进一步的探究:在一个支架的横杆点处用一根细绳悬挂一个小球,小球可以自由摆动,如图,A表示小球静止时的位置,当小强用发声物体靠近小球时,小球从A摆到位置,此时过点作于点,当小球摆到位置时,过点作于点,测得(图中的点在同一平面内).
(1)猜想此时与的位置关系,并说明理由;
(2)求的长.
【答案】(1);见解析
(2)
【分析】本题主要考查了三角形全等的判定和性质,解题的关键是熟练掌握三角形全等的判定和性质.
(1)证明,得出,根据,求出,即可证明结论;
(2)根据,得出,根据,求出结果即可.
【详解】(1)解:,理由如下:
∵于D,于E,
∴,
又∵根据题意得:,,
∴,
∴,
又∵,
∴,
即,
∴;
(2)解:∵,
∴,
又∵,
∴,
答:的长为.
【变式10-1】(23-24八年级·辽宁大连·期末)一天数学课堂上,小明忘记了带圆规,于是他尝试用直角三角板来画角平分线.如图,在的两边上,分别取,将两个直角三角板的直角顶点放在点,处作,的垂线,交点为,一个三角板的斜边与另一个三角板直角边交于点,画射线 就得到的平分线.
【答案】
【分析】本题考查作图之应用与设计作图,全等三角形的判定和性质等知识,证明,推出,即可求得.
【详解】解:如图,作射线,
在和中,
,
,
,
射线平分.
故答案为:.
【变式10-2】(23-24八年级·江苏盐城·期末)已知:如图,,.求证:.
【答案】见解析
【分析】本题考查的是全等三角形的判定与性质,利用证明即可得到结论.
【详解】证明:∵,
在和中,
,
∴.
∴.
【变式10-3】(23-24八年级·陕西西安·期中)如图,已知是的高,E为上一点,交于点F,且,求的度数.
【答案】
【分析】本题考查了全等三角形的判定及性质,能够灵活运用其性质是解题的关键.根据证明得,推出是等腰直角三角形,由此即可解决问题.
【详解】解:∵,
∴,
在和中,
,
∴,
∴,
∵,
∴.
21世纪教育网(www.21cnjy.com)
【人教版】
【题型1 利用SSS证明三角形全等】 1
【题型2 SSS与全等三角形的性质综合应用】 2
【题型3 利用SAS证明三角形全等】 4
【题型4 SAS与全等三角形的性质综合应用】 5
【题型5 利用ASA证明三角形全等】 6
【题型6 ASA与全等三角形的性质综合应用】 7
【题型7 利用AAS证明三角形全等】 9
【题型8 AAS与全等三角形的性质综合应用】 10
【题型9 利用HL证明三角形全等】 11
【题型10 HL与全等三角形的性质综合应用】 12
知识点1:由边边边(SSS)证明两个三角形全等
三边分别相等的两个三角形全等,简写成“边边边”或“SSS”.
当三角形的三边确定后,其形状、大小也随之确定.这也是三角形具有稳定性的原因.
【题型1 利用SSS证明三角形全等】
【例1】(23-24八年级·山西晋中·期末)如图是某款雨伞的实物图,图是该雨伞部分骨架示意图.测得,点,分别是,的三等分点,,那么的依据是( )
A. B. C. D.
【变式1-1】(23-24八年级·全国·课后作业)如图所示,,,用三角形全等的判定“SSS”可证明 或 .
【变式1-2】(23-24八年级·广东广州·期中)如图,已知点,,,在同一条直线上,,,.求证:.
【变式1-3】(23-24·山东淄博·八年级·期末)如图,点D在内部,,.求证:.
【题型2 SSS与全等三角形的性质综合应用】
【例2】(23-24八年级·山东菏泽·阶段练习)阅读并完成下面的推理过程以及括号内的理由:
已知:,,,.求:的度数.
解:因为,(已知)
所以______+______(等式的性质)
即
在和中:
所以( )
所以 (全等三角形的相等)
因为
所以 .
【变式2-1】(23-24八年级·全国·课后作业)如图,已知AE=DB,BC=EF,AC=DF,求证:(1)AC∥DF;(2)CB∥EF.
【变式2-2】(23-24八年级·广东肇庆·阶段练习)如图,已知中,,是边上的中线,试猜想:
(1)与的大小关系;
(2)与的位置关系.并证明你的结论.
【变式2-3】(23-24八年级·吉林·期末)如图,已知点在同一条直线上,.
(1)求证:;
(2)判断的形状,并说明理由.
知识点2:由边角边(SAS)证明两个三角形全等
两边和它们的夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.
此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.
【注意】(1)此方法是证明两个三角形全等最常用的方法之一,应用时,可以从图形上直接观察到三个对应元素必须符合“两边夹角”,即“SAS”,不要误认为有两边一角就能判定两个三角形全等.
(2)在书写时也要按照“边→角→边”的顺序排列条件,必须牢记“边边角”不能作为判定两个三角形全等的条件.
【题型3 利用SAS证明三角形全等】
【例3】(23-24八年级·河南郑州·期末)如图,小明要测量水池的宽,但没有足够长的绳子,聪明的他想了如下办法:先在地上取一个可以直接到达点和点的点,连接并延长到,使,连接并延长到,使,连接并测量出它的长度,则的长度就是的长,理由是根据 (用简写形式即可),可以得到,从而由全等三角形的对应边相等得出结论.
【变式3-1】(23-24八年级·江苏宿迁·阶段练习)如图,点、在上,,要用证,则需添加的条件为 .
【变式3-2】(23-24·云南昆明·八年级·期末)如图,,.求证:.
【变式3-3】(23-24八年级·陕西咸阳·期中)如图,等边中,是的角平分线,为上一点,以为一边且在下方作等边,连接,求证:.
【题型4 SAS与全等三角形的性质综合应用】
【例4】(23-24·陕西·模拟预测)如图,在中,,过点作,且,求证:.
【变式4-1】(23-24八年级·上海·专题练习)如图,在中,已知点、、分别在边、、上,且,,,那么和的大小关系如何?为什么?
解:因为 ,
即.
又因为(已知),
所以 .
在和中,
所以 .
因此.
【变式4-2】(23-24八年级·内蒙古通辽·期中)如图,在中,,,过点作,垂足为,延长至.使得.在边上截取,连结.
(1)求∠的度数.
(2)求证:.
【变式4-3】(23-24八年级·河南郑州·期末)如图,四边形、都是正方形,连接、.求证:
(1);
(2).
知识点3:由角边角(ASA)证明两个三角形全等
两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
用“ASA”来判定两个三角形全等,一定要证明这两个三角形有两个角以及这两个角的夹边分别相等,证明时要加强对夹边的认识.
【题型5 利用ASA证明三角形全等】
【例5】(23-24八年级·河南郑州·期末)如图,为的中点,点为射线上(不与点重合)的任意一点,连接,并使的延长线交射线于点.试说明:.
【变式5-1】(23-24八年级·湖北武汉·期中)一块三角形玻璃被摔成如图所示的四块,小江想去买一块形状、大小与原来一样的玻璃,但是他只想带去其中的两块,则这两块玻璃的编号可以是( )
A.①② B.②④ C.③④ D.①④
【变式5-2】(23-24八年级·山东枣庄·阶段练习)如图,、、、在同一条直线上,,,,试说明:.
【变式5-3】(23-24八年级·河南郑州·期末)已知:点B、E、C、F在一条直线上,.求证:.
【题型6 ASA与全等三角形的性质综合应用】
【例6】(23-24八年级·云南昭通·阶段练习)如图,,,,,则等于 .
【变式6-1】(23-24八年级·重庆·期末)如图,某段河流的两岸是平行的,小开想出了一个不用涉水过河就能测得河的宽度的方案,首先在岸边点B处,选对岸正对的一棵树A,然后沿河岸直行到达树C,继续前行到达点D处,再从点D处沿河岸垂直的方向行走.当到达树A正好被树C遮挡住的点E处时,停止行走,此时的长度即为河岸的宽度.小开这样判断的依据是( )
A. B. C. D.
【变式6-2】(23-24八年级·浙江·期末)如图,在和中,点在边上,,,.
(1)求证:.
(2)若,求的度数.
【变式6-3】(23-24八年级·广东佛山·阶段练习)如图,已知,的平分线恰好交于上一点,已知,,则 .
知识点4:由角角边(AAS)证明两个三角形全等
两角和其中一个角的对边分别相等的两个三角形全等,简写成“角角边”或“AAS”.这一结论很容易由“ASA”推得,将这一结论与“ASA”结合起来,即可得出:两个三角形如果具备两角和一条边对应相等,就可判定其全等.
【题型7 利用AAS证明三角形全等】
【例7】(23-24·陕西西安·八年级·期末)如图,点在上,,,.求证:
【变式7-1】(23-24八年级·山西太原·阶段练习)如图,太阳光线和是平行的,在同一时刻,两根高度相等的木杆的影子是一样长的,这利用了全等图形的性质,其中判断的依据是 .
【变式7-2】(23-24·山东淄博·八年级·期末)如图, 点在的外部,点在上,交于点, ,.求证: .
【变式7-3】(23-24八年级·安徽合肥期末)如图,在四边形中,点在边上,.求证:.
【题型8 AAS与全等三角形的性质综合应用】
【例8】(23-24八年级·河南周口·期中)如图,在中,是边上的高,是边上的高,且交于点F,若,则线段的长为 .
【变式8-1】(23-24八年级·重庆·期末)在中,,过点A作于点D,延长至点E,使得,过点E作,交的延长线于点F,连接.
(1)求证:;
(2)若,,求的度数.
【变式8-2】(23-24八年级·上海普陀·期末)如图,已知,,.试说明的理由.
解:因为(已知),
所以(垂直的意义).
同理 .
所以(等量代换).
在和中,
所以( ).
得 (全等三角形的对应边相等).
又因为(已知),
所以( ).
【变式8-3】(23-24八年级·陕西西安·阶段练习)如图所示,工人赵师傅用10块高度都是的相同长方体新型建筑材料,垒了两堵与地面垂直的墙和,其中于点B,于点E,点P在上,已知,.
(1)求证:;
(2)求的长.
知识点5:由斜边、直角边(HL)证明两个三角形全等
斜边和一条直角边分别相等的两个直角三角形全等,简写成“斜边、直角边”或“HL”.
“HL”定理是直角三角形所独有的,对于一般三角形不成立.
【题型9 利用HL证明三角形全等】
【例9】(23-24八年级·陕西西安·期末)如图,在和中,点B、D、C、E在同一条直线上,点C和点E重合.,,若添加一个条件后可用“”定理证明,添加的条件是( )
A. B. C. D.
【变式9-1】(23-24八年级·陕西榆林·期中)如图,在四边形中,,,是上一点,且,连接、,.求证:.
【变式9-2】(23-24八年级·云南保山·期末)用三角尺可按下面方法画角平分线:如图摆放使得三角板刻度相同,即,画射线,则平分.作图过程用了,那么所用的判定定理是( )
A. B. C. D.
【变式9-3】(23-24八年级·山东济南·期末)如图,在和中,,,与分别为,边上的中线,且,求证:.
【题型10 HL与全等三角形的性质综合应用】
【例10】(23-24八年级·广西贵港·期末)小强在物理课上学习了发声物体的振动试验后,对其作了进一步的探究:在一个支架的横杆点处用一根细绳悬挂一个小球,小球可以自由摆动,如图,A表示小球静止时的位置,当小强用发声物体靠近小球时,小球从A摆到位置,此时过点作于点,当小球摆到位置时,过点作于点,测得(图中的点在同一平面内).
(1)猜想此时与的位置关系,并说明理由;
(2)求的长.
【变式10-1】(23-24八年级·辽宁大连·期末)一天数学课堂上,小明忘记了带圆规,于是他尝试用直角三角板来画角平分线.如图,在的两边上,分别取,将两个直角三角板的直角顶点放在点,处作,的垂线,交点为,一个三角板的斜边与另一个三角板直角边交于点,画射线 就得到的平分线.
【变式10-2】(23-24八年级·江苏盐城·期末)已知:如图,,.求证:.
【变式10-3】(23-24八年级·陕西西安·期中)如图,已知是的高,E为上一点,交于点F,且,求的度数.
21世纪教育网(www.21cnjy.com)
专题12.2 三角形全等的判定(基础篇)【十大题型】
【人教版】
【题型1 利用SSS证明三角形全等】 1
【题型2 SSS与全等三角形的性质综合应用】 4
【题型3 利用SAS证明三角形全等】 8
【题型4 SAS与全等三角形的性质综合应用】 10
【题型5 利用ASA证明三角形全等】 14
【题型6 ASA与全等三角形的性质综合应用】 17
【题型7 利用AAS证明三角形全等】 20
【题型8 AAS与全等三角形的性质综合应用】 23
【题型9 利用HL证明三角形全等】 27
【题型10 HL与全等三角形的性质综合应用】 29
知识点1:由边边边(SSS)证明两个三角形全等
三边分别相等的两个三角形全等,简写成“边边边”或“SSS”.
当三角形的三边确定后,其形状、大小也随之确定.这也是三角形具有稳定性的原因.
【题型1 利用SSS证明三角形全等】
【例1】(23-24八年级·山西晋中·期末)如图是某款雨伞的实物图,图是该雨伞部分骨架示意图.测得,点,分别是,的三等分点,,那么的依据是( )
A. B. C. D.
【答案】D
【分析】本题考查全等三角形的应用,由点,分别是,的三等分点,,得出,根据三边对应相等,证明.解题的关键是熟练掌握全等三角形的判定定理.
【详解】解:∵点,分别是,的三等分点,
∴,,
∵,
∴,
在与中,
,
∴.
故选:D.
【变式1-1】(23-24八年级·全国·课后作业)如图所示,,,用三角形全等的判定“SSS”可证明 或 .
【答案】
【分析】由、、可证出;由、、可证出.综上即可得出结论.
【详解】解:在和中,
,
∴;
在和中,
,
∴.
故答案为:;.
【点睛】本题主要考查全等三角形的判定,熟练掌握全等三角形的判定条件是解题的关键.
【变式1-2】(23-24八年级·广东广州·期中)如图,已知点,,,在同一条直线上,,,.求证:.
【答案】证明见解析.
【分析】本题考查了三角形全等的判定,由,则,即,再根据即可证明,掌握证明三角形全等的判定定理是解题得关键.
【详解】证明:∵,
∴,
即,
在和中,
,
∴.
【变式1-3】(23-24·山东淄博·八年级·期末)如图,点D在内部,,.求证:.
【答案】见解析
【分析】本题考查全等三角形的判定、等腰三角形的判定,由,可知,再利用即可证明结论,熟练掌握全等三角形的判定是解答的关键.
【详解】证明:∵,
∴,
在与中,
,
∴.
【题型2 SSS与全等三角形的性质综合应用】
【例2】(23-24八年级·山东菏泽·阶段练习)阅读并完成下面的推理过程以及括号内的理由:
已知:,,,.求:的度数.
解:因为,(已知)
所以______+______(等式的性质)
即
在和中:
所以( )
所以 (全等三角形的相等)
因为
所以 .
【答案】;;对应角;
【分析】本题考查了全等三角形的判定与性质,主要考查了学生的逻辑推理能力,解题的关键是熟练掌握全等三角形的判定方法;
根据,,得出,再利用证明 ,即可得出结论.
【详解】解:因为,(已知)
所以(等式的性质)
即
在和中:
所以
所以(全等三角形的对应角相等)
因为所以.
故答案为:;;;;;;;;对应角;.
【变式2-1】(23-24八年级·全国·课后作业)如图,已知AE=DB,BC=EF,AC=DF,求证:(1)AC∥DF;(2)CB∥EF.
【答案】(1)证明见解析(2)证明见解析
【详解】试题分析:(1)由SSS证明△ABC≌△DEF,得出对应角相等∠A=∠D,∠ABC=∠DEF,由内错角相等即可得出结论;
(2)由(1)得:∠ABC=∠DEF,得出∠CBE=∠FEB,由内错角相等即可得出结论.
试题解析:(1)∵AE=DB,
∴AE-BE=DB-BE,
即AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠A=∠D,∠ABC=∠DEF,
∴AC∥DF;
(2)由(1)得:∠ABC=∠DEF,
∴∠CBE=∠FEB,
∴CB∥EF.
【变式2-2】(23-24八年级·广东肇庆·阶段练习)如图,已知中,,是边上的中线,试猜想:
(1)与的大小关系;
(2)与的位置关系.并证明你的结论.
【答案】(1)
(2),证明见解析
【分析】(1)本题考查三角形中线的性质和三角形全等的判定与性质,灵活利用三角形全等判定,即可解题.
(2)本题考查利用三角形全等的性质,再结合邻补角互补即可证明该题.
【详解】(1)解:,理由如下:
是边上的中线,
,
在与中,
,
.
(2),理由如下:
证明:(已证),
,
,
,
.
【变式2-3】(23-24八年级·吉林·期末)如图,已知点在同一条直线上,.
(1)求证:;
(2)判断的形状,并说明理由.
【答案】(1)详见解析
(2)是等腰三角形
【分析】本题考查了全等三角形的判定和性质,等腰三角形的判定等知识.
(1)根据即可证明;
(2)由(1)可知,即可得到,即可得出结论.
【详解】(1)证明:在与中,
,
;
(2)解:是等腰三角形.理由:
,
,
,
即是等腰三角形.
知识点2:由边角边(SAS)证明两个三角形全等
两边和它们的夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.
此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.
【注意】(1)此方法是证明两个三角形全等最常用的方法之一,应用时,可以从图形上直接观察到三个对应元素必须符合“两边夹角”,即“SAS”,不要误认为有两边一角就能判定两个三角形全等.
(2)在书写时也要按照“边→角→边”的顺序排列条件,必须牢记“边边角”不能作为判定两个三角形全等的条件.
【题型3 利用SAS证明三角形全等】
【例3】(23-24八年级·河南郑州·期末)如图,小明要测量水池的宽,但没有足够长的绳子,聪明的他想了如下办法:先在地上取一个可以直接到达点和点的点,连接并延长到,使,连接并延长到,使,连接并测量出它的长度,则的长度就是的长,理由是根据 (用简写形式即可),可以得到,从而由全等三角形的对应边相等得出结论.
【答案】(或边角边)
【分析】本题考查了全等三角形的判定,根据题意知,,,可用证明两三角形全等.
【详解】由题意知,,
在和中,
,
.
故答案为:.
【变式3-1】(23-24八年级·江苏宿迁·阶段练习)如图,点、在上,,要用证,则需添加的条件为 .
【答案】/
【分析】本题考查了全等三角形的判定,根据且证,则添加条件为,即可作答.
【详解】解:∵运用证,且
∴添加条件为
即和中
∴
故答案为:
【变式3-2】(23-24·云南昆明·八年级·期末)如图,,.求证:.
【答案】见解析
【分析】本题考查了全等三角形的判定,根据直接证明两三角形全等,即可得证.
【详解】证明:在和中,
∵,
∴
【变式3-3】(23-24八年级·陕西咸阳·期中)如图,等边中,是的角平分线,为上一点,以为一边且在下方作等边,连接,求证:.
【答案】见解析
【分析】本题考查了等边三角形的性质、三角形全等的判定.先根据等边三角形的性质可得,,,从而可得,,再利用即可得证.
【详解】证明:,均为等边三角形,
,,
,
,即,
在和中,,
【题型4 SAS与全等三角形的性质综合应用】
【例4】(23-24·陕西·模拟预测)如图,在中,,过点作,且,求证:.
【答案】见解析
【分析】此题考查了全等三角形的判定与性质,熟练运用全等三角形的判定与性质是解题的关键.
根据等腰三角形的性质、平行线的性质求出,利用证明,根据“全等三角形的对应边相等”即可得证.
【详解】证明:∵,
∴,
∵,
∴,,
∴,
在和中,
,
∴,
∴,
即.
【变式4-1】(23-24八年级·上海·专题练习)如图,在中,已知点、、分别在边、、上,且,,,那么和的大小关系如何?为什么?
解:因为 ,
即.
又因为(已知),
所以 .
在和中,
所以 .
因此.
【答案】见解析
【分析】本题考查了全等三角形的判定和性质,三角形外角的性质,熟练掌握判定定理与性质定理,理清证明思路是写出理由与步骤的关键.
根据三角形外角的性质可得,再根据,证明,然后证明,得到.
【详解】解:因为(三角形的一个外角等于与它不相邻的两个内角的和),
即.
又因为(已知),
所以.
,
在和中,
所以.
因此.
【变式4-2】(23-24八年级·内蒙古通辽·期中)如图,在中,,,过点作,垂足为,延长至.使得.在边上截取,连结.
(1)求∠的度数.
(2)求证:.
【答案】(1)115°
(2)见解析
【分析】此题考查的是全等三角形的判定与性质;
(1)根据得出,进而根据三角形外角的性质可得出答案;
(2)证明,根据全等三角形的性质即可得出.
【详解】(1)解:.
.
,
;
(2)证明:在中,,,
.
.
在和中,
,
,
.
【变式4-3】(23-24八年级·河南郑州·期末)如图,四边形、都是正方形,连接、.求证:
(1);
(2).
【答案】(1)见解析
(2)见解析
【分析】本题主要考查了正方形的性质,三角形全等的判定和性质,三角形内角和定理的应用,解题的关键是根据三角形全等的判定方法,证明.
(1)利用正方形的性质得,,再利用得,即可证明;
(2)由(1)知,再结合条件证得,即.
【详解】(1)证明:∵四边形、都是正方形,
∴,,
∵,,
∴,
在和中,
,
∴,
∴;
(2)解:设与相交于点,与相交于点,
∵,
∴,
又∵,
∴,
∴.
知识点3:由角边角(ASA)证明两个三角形全等
两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
用“ASA”来判定两个三角形全等,一定要证明这两个三角形有两个角以及这两个角的夹边分别相等,证明时要加强对夹边的认识.
【题型5 利用ASA证明三角形全等】
【例5】(23-24八年级·河南郑州·期末)如图,为的中点,点为射线上(不与点重合)的任意一点,连接,并使的延长线交射线于点.试说明:.
【答案】见解析
【分析】本题主要考查了利用证明三角形全等,由P为的中点,可得,再由对顶角相等可得出,结合已知条件可得出.
【详解】解为的中点,
.
又 ,
【变式5-1】(23-24八年级·湖北武汉·期中)一块三角形玻璃被摔成如图所示的四块,小江想去买一块形状、大小与原来一样的玻璃,但是他只想带去其中的两块,则这两块玻璃的编号可以是( )
A.①② B.②④ C.③④ D.①④
【答案】A
【分析】本题考查了全等三角形的应用,学会把实际问题转化为数学问题是解答的关键.
①②两块玻璃是已知两角及其一夹边,可用证明全等来说理.
【详解】解:A、①②两块玻璃是已知两角及其一夹边,可用证明全等,故本选项符合题意;
B、②④两块玻璃是已知两角,无法证明全等,故本选项不符合题意;
C、③④两块玻璃是已知一角,无法证明全等,故本选项不符合题意;
D、①④两块玻璃是已知两角,无法证明全等,故本选项不符合题意.
故选:A.
【变式5-2】(23-24八年级·山东枣庄·阶段练习)如图,、、、在同一条直线上,,,,试说明:.
【答案】见解析
【分析】本题主要考查了全等三角形的判定,先证明,再利用证明即可证明结论.
【详解】解:,
,即,
在和中,
,
) .
【变式5-3】(23-24八年级·河南郑州·期末)已知:点B、E、C、F在一条直线上,.求证:.
【答案】见解析
【分析】此题考查了全等三角形的判定,由平行线的性质得到,,由线段之间的关系得到,即可证明.
【详解】证明:∵,
∴,
∵,
∴,
∵,
∴,
即,
在和中,
,
∴.
【题型6 ASA与全等三角形的性质综合应用】
【例6】(23-24八年级·云南昭通·阶段练习)如图,,,,,则等于 .
【答案】3;
【分析】本题考查三角形全等的判定及性质,根据得到,结合角边角判定即可得到答案;
【详解】解:∵,
∴,
在与中,
∵,
∴,
∴,
∵,,
∴,
故答案为:3.
【变式6-1】(23-24八年级·重庆·期末)如图,某段河流的两岸是平行的,小开想出了一个不用涉水过河就能测得河的宽度的方案,首先在岸边点B处,选对岸正对的一棵树A,然后沿河岸直行到达树C,继续前行到达点D处,再从点D处沿河岸垂直的方向行走.当到达树A正好被树C遮挡住的点E处时,停止行走,此时的长度即为河岸的宽度.小开这样判断的依据是( )
A. B. C. D.
【答案】D
【分析】本题主要考查了全等三角形的判定和性质,解题的关键是熟练掌握三角形全等的判定方法,,,,,.根据,,再根据对顶角相等,利用证明即可.
【详解】解:由题意,得,,
在与中,
∴,
∴,
∴小开这样判断的依据是.
故选:D.
【变式6-2】(23-24八年级·浙江·期末)如图,在和中,点在边上,,,.
(1)求证:.
(2)若,求的度数.
【答案】(1)见详解
(2)
【分析】本题主要考查了全等三角形的判定与性质、等腰三角形的判定与性质等知识,利用“”证明是解题关键.
(1)首先证明,然后利用“”证明即可;
(2)首先根据全等三角形的性质可得,,再结合等腰三角形“等边对等角”的性质可得,然后由求解即可.
【详解】(1)证明:∵,
∴,
∴,
在和中,
,
∴;
(2)∵,,
∴,,
∴,
∴.
【变式6-3】(23-24八年级·广东佛山·阶段练习)如图,已知,的平分线恰好交于上一点,已知,,则 .
【答案】7
【分析】本题考查的是全等三角形的判定和性质、等腰三角形的性质,掌握全等三角形的判定定理和性质定理是解题的关键.延长交的延长线于点,根据等腰三角形的性质得到,利用定理证明,根据全等三角形的性质得到,进而求出.
【详解】解:延长交的延长线于点,
平分,
,
,
,
,
,
平分,
,
在和中,
,
,
,
,
故答案为:7.
知识点4:由角角边(AAS)证明两个三角形全等
两角和其中一个角的对边分别相等的两个三角形全等,简写成“角角边”或“AAS”.这一结论很容易由“ASA”推得,将这一结论与“ASA”结合起来,即可得出:两个三角形如果具备两角和一条边对应相等,就可判定其全等.
【题型7 利用AAS证明三角形全等】
【例7】(23-24·陕西西安·八年级·期末)如图,点在上,,,.求证:
【答案】见详解
【分析】先根据平行线的性质得到,然后根据“”可判断.本题考查了全等三角形的判定:熟练掌握全等三角形的5种判定方法是解决问题的关键.选用哪一种方法,取决于题目中的已知条件.
【详解】解:,
,
在和中,
,
.
【变式7-1】(23-24八年级·山西太原·阶段练习)如图,太阳光线和是平行的,在同一时刻,两根高度相等的木杆的影子是一样长的,这利用了全等图形的性质,其中判断的依据是 .
【答案】
【分析】此题考查全等三角形的应用,解题关键是掌握全等三角形的判定方法.
根据平行线的性质可得,根据题意可得,,然后利用判定.
【详解】解: ,
,
两根高度相同的木杆竖直插在地面上,
∴,,
在和中,
,
∴.
故答案为:.
【变式7-2】(23-24·山东淄博·八年级·期末)如图, 点在的外部,点在上,交于点, ,.求证: .
【答案】见解析
【分析】本题考查了全等三角形的判定,三角形内角和,熟知判定方法是解题的关键.通过,,可得,即可通过证明.
【详解】证明:,
,即,
,
,
即,
在与中,
.
【变式7-3】(23-24八年级·安徽合肥期末)如图,在四边形中,点在边上,.求证:.
【答案】见解析
【分析】
本题考查了全等三角形的判定.利用等角的余角相等求得和,再利用即可证明.
【详解】证明:∵,
∴,
∵,
∴,
∵,
∴.
【题型8 AAS与全等三角形的性质综合应用】
【例8】(23-24八年级·河南周口·期中)如图,在中,是边上的高,是边上的高,且交于点F,若,则线段的长为 .
【答案】6
【分析】本题主要考查了全等三角形的判定与性质,利用证明,得,,即可得出答案.
【详解】解:是边上的高,是边上的高,
,
,
,
在和中,
,
,
,
.
故答案为:6.
【变式8-1】(23-24八年级·重庆·期末)在中,,过点A作于点D,延长至点E,使得,过点E作,交的延长线于点F,连接.
(1)求证:;
(2)若,,求的度数.
【答案】(1)见解析
(2)
【分析】本题主要考查了三角形全等的判定,平行线的性质,三角形内角和定理的应用,解题的关键是数形结合,熟练掌握三角形全等的判定方法.
(1)根据“”证明即可;
(2)根据三角形内角和定理得出,根据,求出即可.
【详解】(1)证明:∵,
∴,
∵,,
∴,
∵,
∴.
(2)解:∵,,
∴,
∴,
∴.
【变式8-2】(23-24八年级·上海普陀·期末)如图,已知,,.试说明的理由.
解:因为(已知),
所以(垂直的意义).
同理 .
所以(等量代换).
在和中,
所以( ).
得 (全等三角形的对应边相等).
又因为(已知),
所以( ).
【答案】见详解
【分析】本题主要考查了全等三角形的判定以及性质,等腰三角形三线合一的性质,垂线的意义,根据垂线得意义可得出,再利用证明,根据全等三角形的性质可得出,再根据等腰三角形三线合一的性质即可证明.
【详解】解:因为(已知),
所以(垂直的意义).
同理.
所以(等量代换).
在和中,
所以().
得(全等三角形的对应边相等).
又因为(已知),
所以(等腰三角形三线合一性质)
【变式8-3】(23-24八年级·陕西西安·阶段练习)如图所示,工人赵师傅用10块高度都是的相同长方体新型建筑材料,垒了两堵与地面垂直的墙和,其中于点B,于点E,点P在上,已知,.
(1)求证:;
(2)求的长.
【答案】(1)见解析
(2)的长为
【分析】题目主要考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题关键.
(1)根据垂直及各角之间的等量代换得出,再由全等三角形的判定即可证明;
(2)由题意得:,,再由全等三角形的性质结合图形求解即可.
【详解】(1)证明:由题意得:,
∴.
∴.
∵,
∴.
∴
在和中
,
∴;
(2)解:由题意得:,,
由(1)得,
∴,.
∴.
答:的长为.
知识点5:由斜边、直角边(HL)证明两个三角形全等
斜边和一条直角边分别相等的两个直角三角形全等,简写成“斜边、直角边”或“HL”.
“HL”定理是直角三角形所独有的,对于一般三角形不成立.
【题型9 利用HL证明三角形全等】
【例9】(23-24八年级·陕西西安·期末)如图,在和中,点B、D、C、E在同一条直线上,点C和点E重合.,,若添加一个条件后可用“”定理证明,添加的条件是( )
A. B. C. D.
【答案】D
【分析】本题考查了全等三角形的判定.熟练掌握全等三角形的判定是解题的关键.根据进行判断作答即可.
【详解】解:由题意知,添加的条件为,
∵,,
∴,
故选:D.
【变式9-1】(23-24八年级·陕西榆林·期中)如图,在四边形中,,,是上一点,且,连接、,.求证:.
【答案】证明见解析
【分析】本题主要考查了全等三角形的判定,平行线的性质,等角对等边,先由平行线的性质求出,再由等角对等边得到,据此利用即可证明.
【详解】证明:∵,
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴.
【变式9-2】(23-24八年级·云南保山·期末)用三角尺可按下面方法画角平分线:如图摆放使得三角板刻度相同,即,画射线,则平分.作图过程用了,那么所用的判定定理是( )
A. B. C. D.
【答案】C
【分析】本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判断和性质是解题的关键.根据已知条件得出得出答案.
【详解】解:∵,,
∴,
在和中,
,
∴.
故选:C.
【变式9-3】(23-24八年级·山东济南·期末)如图,在和中,,,与分别为,边上的中线,且,求证:.
【答案】见解析
【分析】此题考查了全等三角形的判定,根据三角形中线的定义得到,,由,得到,利用即可证明.
【详解】证明:∵与分别为,边上的中线,
∴,,
∵,
∴,
在和中,
,
∴.
【题型10 HL与全等三角形的性质综合应用】
【例10】(23-24八年级·广西贵港·期末)小强在物理课上学习了发声物体的振动试验后,对其作了进一步的探究:在一个支架的横杆点处用一根细绳悬挂一个小球,小球可以自由摆动,如图,A表示小球静止时的位置,当小强用发声物体靠近小球时,小球从A摆到位置,此时过点作于点,当小球摆到位置时,过点作于点,测得(图中的点在同一平面内).
(1)猜想此时与的位置关系,并说明理由;
(2)求的长.
【答案】(1);见解析
(2)
【分析】本题主要考查了三角形全等的判定和性质,解题的关键是熟练掌握三角形全等的判定和性质.
(1)证明,得出,根据,求出,即可证明结论;
(2)根据,得出,根据,求出结果即可.
【详解】(1)解:,理由如下:
∵于D,于E,
∴,
又∵根据题意得:,,
∴,
∴,
又∵,
∴,
即,
∴;
(2)解:∵,
∴,
又∵,
∴,
答:的长为.
【变式10-1】(23-24八年级·辽宁大连·期末)一天数学课堂上,小明忘记了带圆规,于是他尝试用直角三角板来画角平分线.如图,在的两边上,分别取,将两个直角三角板的直角顶点放在点,处作,的垂线,交点为,一个三角板的斜边与另一个三角板直角边交于点,画射线 就得到的平分线.
【答案】
【分析】本题考查作图之应用与设计作图,全等三角形的判定和性质等知识,证明,推出,即可求得.
【详解】解:如图,作射线,
在和中,
,
,
,
射线平分.
故答案为:.
【变式10-2】(23-24八年级·江苏盐城·期末)已知:如图,,.求证:.
【答案】见解析
【分析】本题考查的是全等三角形的判定与性质,利用证明即可得到结论.
【详解】证明:∵,
在和中,
,
∴.
∴.
【变式10-3】(23-24八年级·陕西西安·期中)如图,已知是的高,E为上一点,交于点F,且,求的度数.
【答案】
【分析】本题考查了全等三角形的判定及性质,能够灵活运用其性质是解题的关键.根据证明得,推出是等腰直角三角形,由此即可解决问题.
【详解】解:∵,
∴,
在和中,
,
∴,
∴,
∵,
∴.
21世纪教育网(www.21cnjy.com)
