人教版2024-2025学年八年级数学上册举一反三专题12.3三角形全等的判定(探索篇)【八大题型】(学生版+解析)
文档属性
| 名称 | 人教版2024-2025学年八年级数学上册举一反三专题12.3三角形全等的判定(探索篇)【八大题型】(学生版+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 13:09:58 | ||
图片预览


文档简介
专题12.3 三角形全等的判定(探索篇)【八大题型】
【人教版】
【题型1 添加条件使三角形全等】 1
【题型2 确定全等三角形的对数】 2
【题型3 网格中确定全等三角形】 3
【题型4 灵活选用判定方法证明全等】 5
【题型5 多次证全等求解或证明结论】 6
【题型6 由全等三角形的判定与性质确定线段之间的关系】 7
【题型7 全等三角形的动态问题】 9
【题型8 全等三角形的应用】 10
知识点:全等三角形的判定
判定两个三角形全等常用的思路方法如下:
【题型1 添加条件使三角形全等】
【例1】(23-24八年级·山东东营·期中)如图,在和中,点B、D、C在同一直线上,已知,,添加以下条件后,仍不能判定的是( )
A. B. C. D.
【变式1-1】(23-24八年级·河南信阳·期中)在和中,,有下列条件:①;②;③;④;⑤.请你从中选择两个条件: ,使,你判断它们全等的根据是 .
【变式1-2】(23-24八年级·江苏徐州·期中)如图,已知,,要使,则需要添加的条件是 .(写一个即可)
【变式1-3】(23-24八年级·湖北襄阳·期末)如图,点B、E、C、F四点在一条直线上,∠A=∠D,AB//DE,老师说:再添加一个条件就可以使△ABC≌△DEF.下面是课堂上三个同学的发言,甲说:添加AB=DE;乙说:添加AC//DF;丙说:添加BE=CF.
(1)甲、乙、丙三个同学说法正确的是________;
(2)请你从正确的说法中选择一种,给出你的证明.
【题型2 确定全等三角形的对数】
【例2】(23-24八年级·河南信阳·期中)如图,在中,,连接相交于点,连接,则图中共有全等三角形( )
A.5对 B.4对 C.3对 D.2对
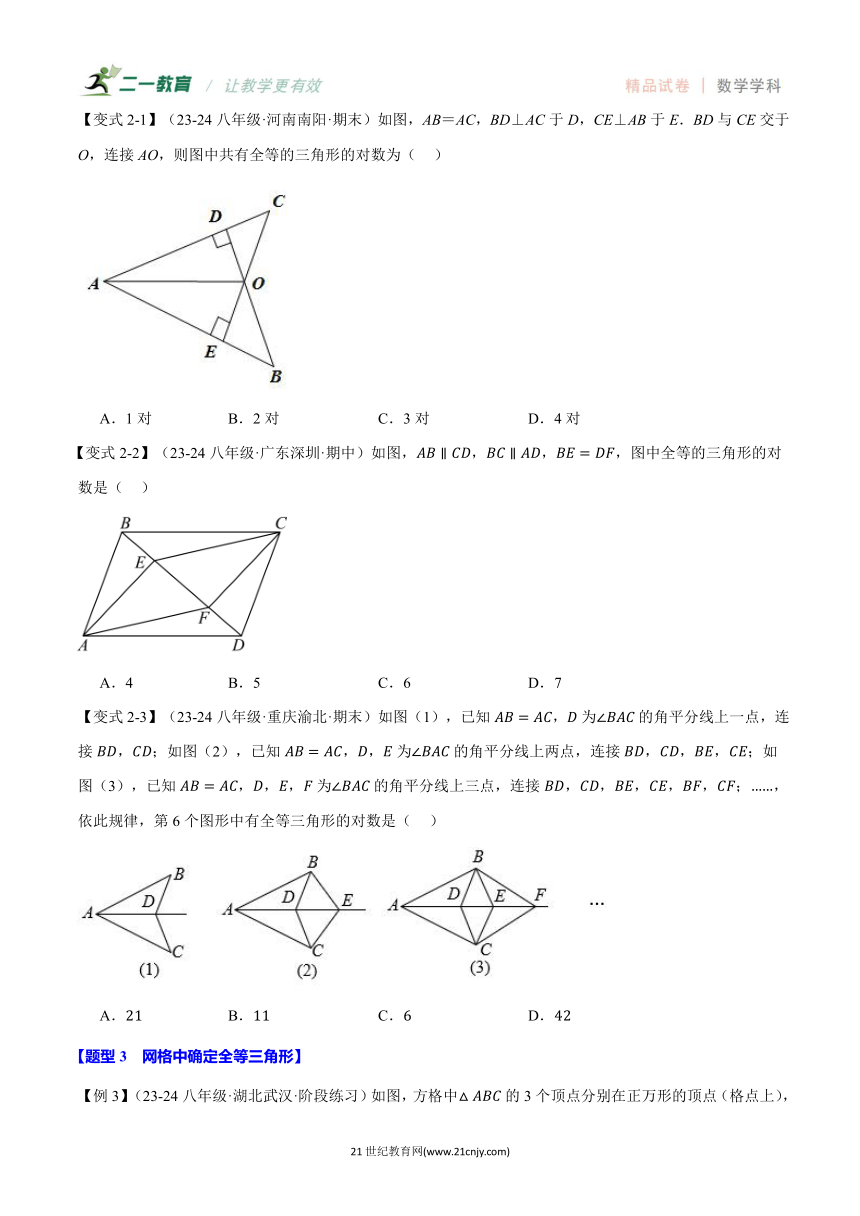
【变式2-1】(23-24八年级·河南南阳·期末)如图,AB=AC,BD⊥AC于D,CE⊥AB于E.BD与CE交于O,连接AO,则图中共有全等的三角形的对数为( )
A.1对 B.2对 C.3对 D.4对
【变式2-2】(23-24八年级·广东深圳·期中)如图,,,,图中全等的三角形的对数是( )
A.4 B.5 C.6 D.7
【变式2-3】(23-24八年级·重庆渝北·期末)如图(1),已知,为的角平分线上一点,连接,;如图(2),已知,,为的角平分线上两点,连接,,,;如图(3),已知,,,为的角平分线上三点,连接,,,,,;,依此规律,第6个图形中有全等三角形的对数是( )
A. B. C. D.
【题型3 网格中确定全等三角形】
【例3】(23-24八年级·湖北武汉·阶段练习)如图,方格中的3个顶点分别在正万形的顶点(格点上),这样的三角形叫格点三角形,图中与(不含)全等的格点三角形共有( )个
A.4 B.5 C.8 D.7
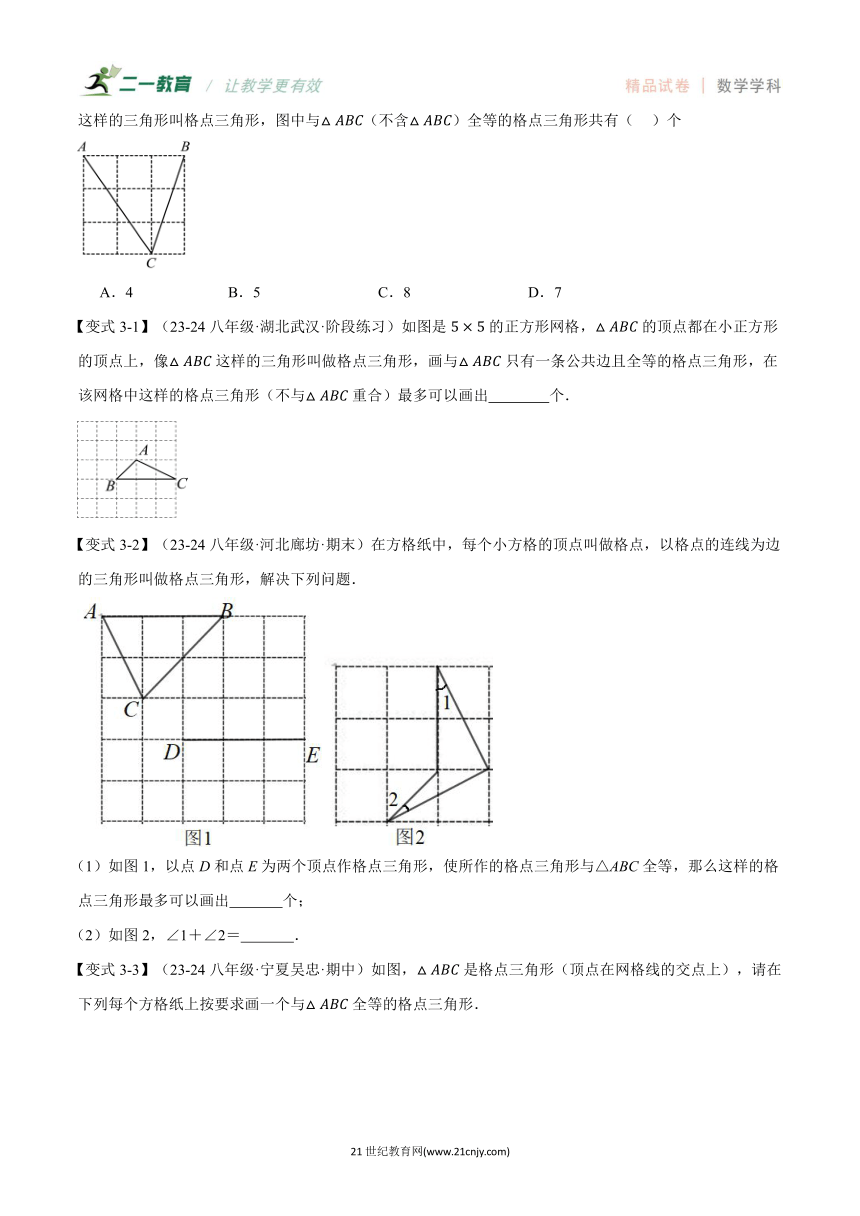
【变式3-1】(23-24八年级·湖北武汉·阶段练习)如图是的正方形网格,的顶点都在小正方形的顶点上,像这样的三角形叫做格点三角形,画与只有一条公共边且全等的格点三角形,在该网格中这样的格点三角形(不与重合)最多可以画出 个.
【变式3-2】(23-24八年级·河北廊坊·期末)在方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形,解决下列问题.
(1)如图1,以点D和点E为两个顶点作格点三角形,使所作的格点三角形与△ABC全等,那么这样的格点三角形最多可以画出 个;
(2)如图2,∠1+∠2= .
【变式3-3】(23-24八年级·宁夏吴忠·期中)如图,是格点三角形(顶点在网格线的交点上),请在下列每个方格纸上按要求画一个与全等的格点三角形.
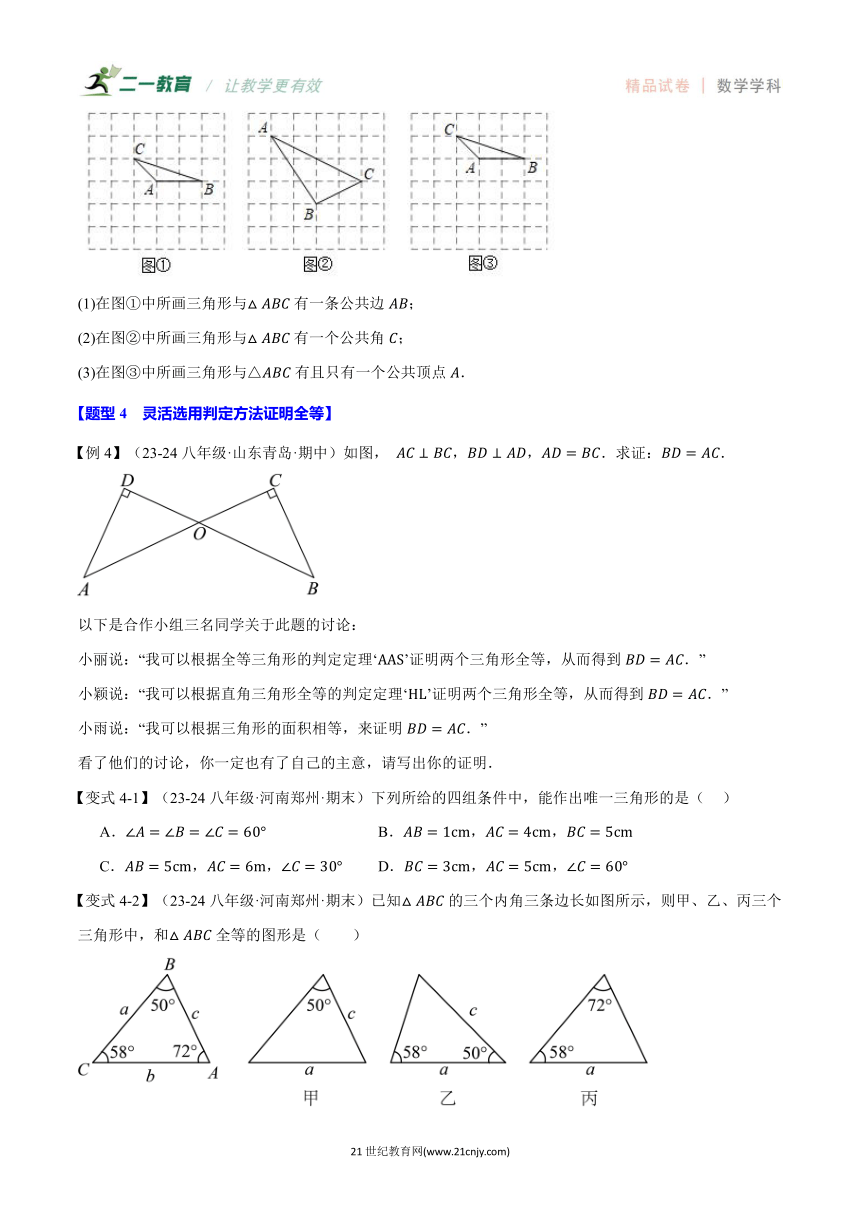
(1)在图①中所画三角形与有一条公共边;
(2)在图②中所画三角形与有一个公共角;
(3)在图③中所画三角形与△有且只有一个公共顶点.
【题型4 灵活选用判定方法证明全等】
【例4】(23-24八年级·山东青岛·期中)如图, ,,.求证:.
以下是合作小组三名同学关于此题的讨论:
小丽说:“我可以根据全等三角形的判定定理‘’证明两个三角形全等,从而得到.”
小颖说:“我可以根据直角三角形全等的判定定理‘’证明两个三角形全等,从而得到.”
小雨说:“我可以根据三角形的面积相等,来证明.”
看了他们的讨论,你一定也有了自己的主意,请写出你的证明.
【变式4-1】(23-24八年级·河南郑州·期末)下列所给的四组条件中,能作出唯一三角形的是( )
A. B.,,
C.,, D.,,
【变式4-2】(23-24八年级·河南郑州·期末)已知的三个内角三条边长如图所示,则甲、乙、丙三个三角形中,和全等的图形是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
【变式4-3】(23-24八年级·河北保定·期末)(1)阅读下题及证明过程
已知:如图,是的边上一点,是上一点,,.
求证:.
证明:在和中,
因为,,,
所以………………第一步
所以………………第二步
上面的证明过程是否正确?若正确,请写出每一步推理的依据;若不正确,请指出错在哪一步,并写出你认为正确的证明过程.
(2)如果两个锐角三角形的两组边分别相等,且其中一组等边的对角相等,那么这两个三角形全等吗?请说明理由.
【题型5 多次证全等求解或证明结论】
【例5】(23-24八年级·黑龙江哈尔滨·期末)已知:是的角平分线,且
(1)如图1,求证:;
(2)如图2,,点E在AD上,连接并延长交于点F,交的延长线于点G,且,连接.
①求证:;
②若,且,求AC的长.
【变式5-1】(23-24八年级·河南洛阳·期末)已知:如图,,,与相交于点,连接.
证明:
(1);
(2)平分.
【变式5-2】(23-24八年级·广西百色·期末)如图,已知,于点D,于点B,.
(1)求证:;
(2)连接交于点O,试判断与之间的数量关系,并说明理由.
【变式5-3】(23-24八年级·重庆·期末)如图1,在等边三角形中,点D在上,点E在上,,交于点F,于点G,延长交于点H,.
(1)求证:.
(2)如图2,连接,若,求证:点F是的中点.
【题型6 由全等三角形的判定与性质确定线段之间的关系】
【例6】(23-24八年级·江西南昌·期末)如图,是的角平分线.
(1)若,求证:;
(2)当时,与的数量关系如何?说说你的理由.
【变式6-1】(23-24八年级·广东潮州·阶段练习)在中,,,直线经过点,且于,于.
(1)当直线绕点旋转到图的位置时,求证:
①;
②;
(2)当直线绕点旋转到图的位置时,,,求线段的长.
【变式6-2】(23-24八年级·重庆·期末)如图,在中,,,过点B作,且,点B作交于点F,连接.
(1)如图1,若,且,求的度数;
(2)如图2,若,求证:.
【变式6-3】(23-24八年级·重庆·期末)在中,和的角平分线相交于点.
(1)若,求的度数;
(2)延长至点,过点作的平行线交于点,若,求证:.
【题型7 全等三角形的动态问题】
【例7】(23-24八年级·湖南郴州·期中)如图,已知中,,厘米,厘米,点为的中点,如果点在线段上以每秒厘米的速度由点向点运动,同时,点在线段上以每秒厘米的速度由点向点运动,设运动时间为秒 .
(1)用含的代数式表示的长度.
(2)若点、的运动速度相等,经过秒后,与是否全等,请说明理由;
(3)若点、的运动速度不相等,当点的运动速度为多少时,能够使与全等?
【变式7-1】(23-24八年级·广东潮州·期中)如图,在矩形中,,点E在线段上,且,动点P在线段上,从点A出发以的速度向点B运动,同时点Q在线段上.以的速度由点B向点C运动,当与全等时,v的值为( )
A.2 B.4 C.4或 D.2或
【变式7-2】(23-24八年级·湖南郴州·期中)如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为 .
【变式7-3】(23-24八年级·河南郑州·期末)如图,在中,为高线,.点为上一点,,连接,交于点,若.
(1)猜想线段与的位置关系,并证明;
(2)若动点从点出发沿射线以每秒6个单位长度的速度运动,运动的时间为秒.
①当点在线段上时,是否存在的值,使得的面积为27?若存在,请求出的值;若不存在,请说明理由;
②动点从点出发沿线段以每秒2个单位长度的速度向终点运动,,两点同时出发,当点到达点时,,两点同时停止运动.设运动时间为秒,点是直线上一点,且,当与全等时,请直接写出的值.
【题型8 全等三角形的应用】
【例8】(23-24八年级·贵州铜仁·期末)某同学根据数学知识原理制作了如图所示的一个测量工具----拐尺,其中O为AB的中点,CA⊥AB,BD⊥AB,CA=BD,现要测量一透明隔离房间的深度,如何使用此测量工具,说明理由.
【变式8-1】(23-24八年级·陕西西安·期中)如图,小刚站在河边的点A处,在河对面(小刚的正北方向)的点B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了20步到达一棵树C处,接着再向前走了20步到达D处,然后他左转直行,从点D处开始计步,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他恰好走了74步,并且小刚一步大约0.5米.由此小刚估计出了在点A处时他与电线塔的距离,请问他的做法是否合理?若合理,请求出在点A处时他与电线塔的距离;若不合理,请说明理由.
【变式8-2】(23-24八年级·陕西西安·期末)小乐与朋友们周末去游乐园乘坐海盗船游玩,想了解海盗船摆动到最高点位置时的高度.如图,当静止时海盗船位于铅垂线上,转轴到地面的距离,在乘坐的过程中,当海盗船静止在点处时,,此时测得点到铅垂线的距离,当船头从处摆动到处时发现船头处在最高位置处,此时,.求点到地面的距离.
【变式8-3】(23-24八年级·河南郑州·期末)茗阳阁位于河南省信阳市浉河区茶韵路一号,建成于2007年4月29日,是信阳新建的城市文化与形象的代表建筑之一.设两点分别为茗阳阁底座的两端(其中两点均在地面上).因为两点间的实际距离无法直接测量,某学习小组分别设计出了如下两种方案:甲:如图1,在平地上取一个可以直接到达点的点O,连接并延长到点C,连接并延长到点D,使,连接,测出的长即可.乙:如图2,先确定直线,过点B作,在点D处用测角仪确定,射线交直线于点C,最后测量的长即可得线段的长.
(1)请用所学知识论证甲、乙两种方案的合理性;
(2)如果让你参与测量,你会选择哪一种方案?请说明理由.21世纪教育网(www.21cnjy.com)
专题12.3 三角形全等的判定(探索篇)【八大题型】
【人教版】
【题型1 添加条件使三角形全等】 2
【题型2 确定全等三角形的对数】 5
【题型3 网格中确定全等三角形】 8
【题型4 灵活选用判定方法证明全等】 12
【题型5 多次证全等求解或证明结论】 18
【题型6 由全等三角形的判定与性质确定线段之间的关系】 24
【题型7 全等三角形的动态问题】 31
【题型8 全等三角形的应用】 37
知识点:全等三角形的判定
判定两个三角形全等常用的思路方法如下:
【题型1 添加条件使三角形全等】
【例1】(23-24八年级·山东东营·期中)如图,在和中,点B、D、C在同一直线上,已知,,添加以下条件后,仍不能判定的是( )
A. B. C. D.
【答案】D
【分析】本题考查了全等三角形的判定.将各个选项依次代入题目当中,再根据全等三角形的判定方法依次判断即可.一般三角形全等的判定方法有、、、,注意没有.熟练掌握全等三角形的判定方法是解题的关键.
【详解】解:A、若添加,则可根据证明,故A选项不符合题意;
B、若添加,则可得,则可根据证明,故B选项不符合题意;
C、若添加,则可根据证明,故C选项不符合题意;
D、若添加,则成了,不能证明,故D选项符合题意.
故选:D
【变式1-1】(23-24八年级·河南信阳·期中)在和中,,有下列条件:①;②;③;④;⑤.请你从中选择两个条件: ,使,你判断它们全等的根据是 .
【答案】 ②③(答案不唯一)
【分析】本题考查三角形全等的判定方法,根据四个选项所给条件结合判定两个三角形全等的方法分别进行分析即可.
【详解】解:∵,添加②;③;可利用判定;
添加③;④,可利用判定;
添加⑤;③,可利用判定;
故答案为:答案不唯一,如②③;SAS.
【变式1-2】(23-24八年级·江苏徐州·期中)如图,已知,,要使,则需要添加的条件是 .(写一个即可)
【答案】或或(写一个即可)
【分析】本题考查全等三角形的判定,判定两个三角形全等的一般方法有:、、、、.由,可得,再根据题干中的条件,可添加角相等或边相等即可.
【详解】解:添加,
,
,
又 ,,
,
添加,
,
,
又 ,,
,
添加,
,
,
又 ,,
,
故答案为:或或(写一个即可).
【变式1-3】(23-24八年级·湖北襄阳·期末)如图,点B、E、C、F四点在一条直线上,∠A=∠D,AB//DE,老师说:再添加一个条件就可以使△ABC≌△DEF.下面是课堂上三个同学的发言,甲说:添加AB=DE;乙说:添加AC//DF;丙说:添加BE=CF.
(1)甲、乙、丙三个同学说法正确的是________;
(2)请你从正确的说法中选择一种,给出你的证明.
【答案】(1)甲、丙;(2)见详解
【分析】(1)根据平行线的性质,由AB∥DE可得∠B=∠DEC,再加上条件∠A=∠D,只需要添加一个能得出对应边相等的条件,即可证明两个三角形全等,添加AC//DF不能证明△ABC≌△DEF;
(2)添加AB=DE,再由条件AB∥DE可得∠B=∠DEC,然后再利用ASA判定△ABC≌△DEF即可.
【详解】(1)解:∵AB//DE,
∴∠B=∠DEC,
又∵∠A=∠D,
∴添加AB=DE,可得△ABC≌△DEF(ASA);添加BE=CF,可得BC=EF,可得△ABC≌△DEF(AAS)
∴说法正确的是:甲、丙,
故答案为:甲、丙;
(2)选“甲”,理由如下:
证明:∵AB∥DE,
∴∠B=∠DEC,
在△ABC和△DEF中
∴△ABC≌△DEF(ASA).
【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
【题型2 确定全等三角形的对数】
【例2】(23-24八年级·河南信阳·期中)如图,在中,,连接相交于点,连接,则图中共有全等三角形( )
A.5对 B.4对 C.3对 D.2对
【答案】A
【分析】本题考查全等三角形的判定,根据题中条件,数形结合,利用两个三角形全等的判定定理逐个验证即可得到答案,熟练掌握两个三角形全等的判定定理是解决问题的关键.
【详解】解:①由,,根据可得;
②由可得,
由可得,则由,,,根据可得;
③由可得,则由,,根据可得;
④由可得,则由,,根据可得;
⑤由可得;由可得;;根据可得;
综上所述,图中共有全等三角形5对,
故选:A.
【变式2-1】(23-24八年级·河南南阳·期末)如图,AB=AC,BD⊥AC于D,CE⊥AB于E.BD与CE交于O,连接AO,则图中共有全等的三角形的对数为( )
A.1对 B.2对 C.3对 D.4对
【答案】D
【分析】根据AB=AC,BD⊥AC于D,CE⊥AB于E,∠CAE=∠BAD,可证明△CAE≌△BAD,得出AD=AE,∠C=∠B,根据AAS可证明△DCO≌△EBO,得出CO=BO,利用SSS证得△ACO≌△ABO,利用HL证得△DAO≌△EAO,由此得出共有全等的三角形的对数为4对.
【详解】解:由题意可得△CAE≌△BAD,△DCO≌△EBO,△ACO≌△ABO,△DAO≌△EAO共4对三角形全等.
故选:D.
【点睛】本题考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
【变式2-2】(23-24八年级·广东深圳·期中)如图,,,,图中全等的三角形的对数是( )
A.4 B.5 C.6 D.7
【答案】C
【分析】根据全等三角形得判定定理,依次证明三角形全等,即可求解.
【详解】解:,,
,,
在与中,
,
,
,,
在与中,
,
,
,
,
,
,
在与中,
,
同理可得,
,
,
即6对全等三角形.
故选:C.
【点睛】本题考查了全等三角形的判定,能正确根据定理进行推论是解题的关键.
【变式2-3】(23-24八年级·重庆渝北·期末)如图(1),已知,为的角平分线上一点,连接,;如图(2),已知,,为的角平分线上两点,连接,,,;如图(3),已知,,,为的角平分线上三点,连接,,,,,;,依此规律,第6个图形中有全等三角形的对数是( )
A. B. C. D.
【答案】A
【分析】设第个图形中有为正整数)个全等三角形,根据各图形中全等三角形对数的变化可找出变化规律“为正整数)”,再代入即可求出结论.
【详解】解:设第个图形中有为正整数)个全等三角形.
图(1),在和中,
,
,
;
同理,可得:,,,,
为正整数),
.
故选:A.
【点睛】本题考查了全等三角形的判定以及规律型:图形的变化类,根据各图形中全等三角形对数的变化,找出变化规律“为正整数)”是解题的关键.
【题型3 网格中确定全等三角形】
【例3】(23-24八年级·湖北武汉·阶段练习)如图,方格中的3个顶点分别在正万形的顶点(格点上),这样的三角形叫格点三角形,图中与(不含)全等的格点三角形共有( )个
A.4 B.5 C.8 D.7
【答案】D
【分析】
本题考查全等三角形的判定,根据全等三角形的判定方法,结合网格的特点,画出图形,即可得出结果.
【详解】解:如图所示以正方形一边为三角形的边都可作两个全等的三角形,
所以共有8个全等三角形,除去外有7个与全等的三角形.即:
故选D.
【变式3-1】(23-24八年级·湖北武汉·阶段练习)如图是的正方形网格,的顶点都在小正方形的顶点上,像这样的三角形叫做格点三角形,画与只有一条公共边且全等的格点三角形,在该网格中这样的格点三角形(不与重合)最多可以画出 个.
【答案】
【分析】本题考查了全等三角形、格点三角形的定义,可以以为公共边和以为公共边分别画出个三角形,以为公共边不可以画出三角形,即可得出答案,采用数形结合的思想是解此题的关键.
【详解】解:如图所示:
,
以为公共边可以画出、、三个三角形,
以为公共边可以画出、、三个三角形,
故可以画出个,
故答案为:.
【变式3-2】(23-24八年级·河北廊坊·期末)在方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形,解决下列问题.
(1)如图1,以点D和点E为两个顶点作格点三角形,使所作的格点三角形与△ABC全等,那么这样的格点三角形最多可以画出 个;
(2)如图2,∠1+∠2= .
【答案】 4 45°/45度
【分析】(1)观察图形可知:DE与AC是对应边,B点的对应点在DE上方两个,在DE下方两个共有4个满足要求的点,也就有四个全等三角形;
(2)由图可知∠1=∠3,∠2+∠3=45°,从而可得结论.
【详解】解:(1)根据题意,运用SSS可得与△ABC全等的三角形有4个,线段DE的上方有两个点,下方也有两个点.
故答案为:4.
(2)由图可知△ABC≌△EDC,
∴∠1=∠3,
而∠2+∠3=45°,
∴∠1+∠2=45°,
故答案为:45°.
【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL,做题时要做到不重不漏.
【变式3-3】(23-24八年级·宁夏吴忠·期中)如图,是格点三角形(顶点在网格线的交点上),请在下列每个方格纸上按要求画一个与全等的格点三角形.
(1)在图①中所画三角形与有一条公共边;
(2)在图②中所画三角形与有一个公共角;
(3)在图③中所画三角形与△有且只有一个公共顶点.
【答案】(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据题意以及网格的特点根据轴对称画出图形即可;
(2)根据题意以及网格的特点根据轴对称画出图形即可;
(3)根据题意以及网格的特点画出图形即可.
【详解】(1)如图①所示,△ABD即为所求;
(2)如图②所示,△DEC即为所求;
(3)如图③所示,△AED即为所求,
【点睛】本题考查了作图-应用与设计作图、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题.
【题型4 灵活选用判定方法证明全等】
【例4】(23-24八年级·山东青岛·期中)如图, ,,.求证:.
以下是合作小组三名同学关于此题的讨论:
小丽说:“我可以根据全等三角形的判定定理‘’证明两个三角形全等,从而得到.”
小颖说:“我可以根据直角三角形全等的判定定理‘’证明两个三角形全等,从而得到.”
小雨说:“我可以根据三角形的面积相等,来证明.”
看了他们的讨论,你一定也有了自己的主意,请写出你的证明.
【答案】见解析
【分析】本题目考查了三角形全等的判定方法,解题关键是熟练掌握三角形全等的判定定理是解题的关键;
①根据垂线的知识可得,在结合证明,最后根据全等三角形的性质得出结论;②连接,根据直角三角形的,证明,即可得出结论;③连接,证明,可得,再结合三角形面积计算方法即可得出结论;④连接,证明,得,,在利用证明,得出结论.
【详解】小丽方法:
,,
.
在和中,
,.
,即.
小颖方法:
连接.
,,,
.
在和中,
.
.
小雨方法:
连接.
,
.
在和中,
,
,
.即.
又 ,,
,
,
.
方法4:连接,
,,
.
在和中,
,,
,
在和中,
,
.
【变式4-1】(23-24八年级·河南郑州·期末)下列所给的四组条件中,能作出唯一三角形的是( )
A. B.,,
C.,, D.,,
【答案】D
【分析】本题主要考查了构成三角形的条件.熟练掌握三角形全等的判定方法,三角形三边关系,是解决问题的关键.
根据三角形三边的关系对B进行判断;根据全等三角形的判定方法对A、C、D进行判断.
【详解】A.,
不符合三角形全等判定条件,不能作出唯一三角形;
B.,,,
这里,不符合三角形三边关系,不能作出三角形;
C.,,,
两边和其中一边的对角对应相等的两个三角形不一定全等,不能作出唯一三角形;
D.,,,
两边及夹角对应相等的两个三角形全等,能作出唯一三角形.
故选:D.
【变式4-2】(23-24八年级·河南郑州·期末)已知的三个内角三条边长如图所示,则甲、乙、丙三个三角形中,和全等的图形是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
【答案】B
【分析】本题考查全等三角形的判定方法,掌握三角形判定方法是解题的关键.
根据三角形判定方法判断即可解答.
【详解】解:甲与不符合两边对应相等,且夹角相等,
∴甲和已知三角形不全等;
乙与符合两边对应相等,且夹角相等,
∴根据可判定乙和与全等;
丙与符合两角对应相等,且其中一角的对边相等,
∴根据可判定丙和与全等.
故选:B.
【变式4-3】(23-24八年级·河北保定·期末)(1)阅读下题及证明过程
已知:如图,是的边上一点,是上一点,,.
求证:.
证明:在和中,
因为,,,
所以………………第一步
所以………………第二步
上面的证明过程是否正确?若正确,请写出每一步推理的依据;若不正确,请指出错在哪一步,并写出你认为正确的证明过程.
(2)如果两个锐角三角形的两组边分别相等,且其中一组等边的对角相等,那么这两个三角形全等吗?请说明理由.
【答案】(1)不正确;错在第一步,详见解析;(2)全等,详见解析
【分析】本题考查了全等三角形的判定与性质,等腰三角形的判定与性质,熟练掌握全等三角形的判定与性质是解答本题的关键.
(1)根据两边及其中一边的对角对应相等的两个三角形不一定全等,可知第一步错误,证明时先根据等腰三角形的性质及判定,可逐步推得,再根据“边边边”判定三角形全等即可;
(2)先写出已知,求证与证明,“已知,在锐角三角形和锐角三角形中,,,.求证:.”过点A作于点D,过点作于点,先根据“角角边”证明,得到,再根据“”定理证明,得到,最后由“ 角角边”即可证得结果.
【详解】(1)不正确;错在第一步.
证明:在△BEC中,∵,
∴,
∵,
,
,
在和中,
,
;
(2)全等.理由如下:
已知:如图,在锐角三角形和锐角三角形中,
,,.
求证:.
证明:过点A作于点D,过点作于点,
,
在和中,
,
,
,
在和中,
,
,
,
在和中,
,
.
【题型5 多次证全等求解或证明结论】
【例5】(23-24八年级·黑龙江哈尔滨·期末)已知:是的角平分线,且
(1)如图1,求证:;
(2)如图2,,点E在AD上,连接并延长交于点F,交的延长线于点G,且,连接.
①求证:;
②若,且,求AC的长.
【答案】(1)见解析
(2)①证明见解析②6
【分析】本题主要考查了全等三角形的性质与判定以及角平分线的定义.
(1)用证明,即得;
(2)①证明可得,再用证明,即得;②过作于,由,可得,,而,,即得,根据,可求.
【详解】(1)证明:是的角平分线,
,
,
,
在和中,
,
,
;
(2)①,,,
,
,
在和中,
,
,
,
在和中,
,
,
;
②过作于,如图:
由①知:,
,
,
,
由①知:,
,
,
,
,
∴.
【变式5-1】(23-24八年级·河南洛阳·期末)已知:如图,,,与相交于点,连接.
证明:
(1);
(2)平分.
【答案】(1)见解析
(2)见解析
【分析】本题考查全等三角形的知识,解题的关键是掌握全等三角形的判定和性质,等边对等角,角平分线的性质,即可.
(1)根据,,得,推出,则,根据,则,则,即可得;
(2)由(1)得,,,推出,则,即可.
【详解】(1)证明如下:
∵,,
∴,
∴,
在和,
,
∴,
∴,
∵,
∴,
∴,
∴.
(2)证明:∵,
∴,
∴,
即平分.
【变式5-2】(23-24八年级·广西百色·期末)如图,已知,于点D,于点B,.
(1)求证:;
(2)连接交于点O,试判断与之间的数量关系,并说明理由.
【答案】(1)见解析
(2),见解析
【分析】本题考查了全等三角形的判定与性质,熟练掌握相关判定定理是解决本题的关键.
(1)根据证明,再根据全等三角形的性质即可得;
(2)根据证明,再根据全等三角形的性质即可得.
【详解】(1)证明:如图所示,
∵,
∴
在和中,
,
∴
∴;
(2)解:
理由如下:
如图,
在和中,
,
∴,
∴.
【变式5-3】(23-24八年级·重庆·期末)如图1,在等边三角形中,点D在上,点E在上,,交于点F,于点G,延长交于点H,.
(1)求证:.
(2)如图2,连接,若,求证:点F是的中点.
【答案】(1)见解析
(2)见解析
【分析】本题考查了全等三角形的判定和性质,等边三角形的性质,添加恰当辅助线构造全等三角形是解题的关键.
(1)由可证,可得;
(2)延长交于点Q,由可证,可得,由可证,可得,可得结论.
【详解】(1)∵是等边三角形,
∴,,
∵,,
∴,,
∴,
∴,
在和中,
,
∴,
∴;
(2)如图,延长交于点Q,
∵,,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∴点F是的中点.
【题型6 由全等三角形的判定与性质确定线段之间的关系】
【例6】(23-24八年级·江西南昌·期末)如图,是的角平分线.
(1)若,求证:;
(2)当时,与的数量关系如何?说说你的理由.
【答案】(1)见解析
(2),理由见解析
【分析】(1)延长至E,使,连接,运用证明,可得结论;
(2)在的延长线上取点F,使,连接,根据推导得到结论.
【详解】(1)证明:延长至E,使,连接.
∵,
∴.
∵平分,
∴.
在与中,
,
∴.
∴.
∵,
∴
∵,
∴.
(2)解:.
理由:在的延长线上取点F,使,连接.
∴,
又∵,
∴.
∵,
∴.
∵是的角平分线,
∴,
在与中,
,
∴.
∴.
【点睛】本题考查全等三角形的判定和性质,角平分线的定义,三角形外角性质,等腰三角形的判定和性质.正确的作出辅助线是解题关键.
【变式6-1】(23-24八年级·广东潮州·阶段练习)在中,,,直线经过点,且于,于.
(1)当直线绕点旋转到图的位置时,求证:
①;
②;
(2)当直线绕点旋转到图的位置时,,,求线段的长.
【答案】(1)见解析,见解析;
(2).
【分析】(1)由已知推出,因为,,推出,根据即可得到答案;
由得到,,即可求出答案;
()与()证法类似可证出,能推出,得到,,代入已知即可得到答案,
本题考查了全等三角形的性质和判定,同角的余角相等,垂直的定义,熟练掌握知识点的应用是解题的关键.
【详解】(1)证明:∵,,
∴,
∵,
∴,,
∴,
在和中,
,
∴;
证明:由()知:,
∴,,
∵,
∴;
(2)证明:∵,,
∴,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,,
∴.
【变式6-2】(23-24八年级·重庆·期末)如图,在中,,,过点B作,且,点B作交于点F,连接.
(1)如图1,若,且,求的度数;
(2)如图2,若,求证:.
【答案】(1)
(2)见解析
【分析】本题考查等腰三角形的性质、全等三角形的判定与性质、三角形的外角性质、平行线的性质等知识,熟练运用全等三角形的性质探究线段间的关系是解答的关键.
(1)先根据平行线的性质得到,,再根据等腰三角形的性质求得,,进而利用三角形的外角性质求解即可;
(2)先求得,在上截取,连接,分别证明和得到,进而可得结论.
【详解】(1)解:∵,,,
∴,,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
(2)证明:∵,,
∴,
∵,
∴,
如图,在上截取,连接,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,,
∴,
在和中,
,
∴,
∴,
∴,
∴.
【变式6-3】(23-24八年级·重庆·期末)在中,和的角平分线相交于点.
(1)若,求的度数;
(2)延长至点,过点作的平行线交于点,若,求证:.
【答案】(1);
(2)证明见解析.
【分析】()根据角平分线的定义,三角形内角和定理即可求解;
()在上截取,连接,证明,,再根据性质即可求证;
本题考查了角平分线的定义,三角形内角和定理,三角形全等的性质与判定,平行线的性质,熟练掌握知识点的应用是解题的关键.
【详解】(1)解:∵,
∴,
∵和的角平分线相交于点,
∴,,
∴,
∴;
(2)证明:如图,在上截取,连接,
∵平分,
∴垂直平分,
∴,
∵,
∴,
又∵,
∴,
∴,
∴,
又∵,
∴,
∵平分,
∴,
∴,
∴,
∴,
∵,
∴.
【题型7 全等三角形的动态问题】
【例7】(23-24八年级·湖南郴州·期中)如图,已知中,,厘米,厘米,点为的中点,如果点在线段上以每秒厘米的速度由点向点运动,同时,点在线段上以每秒厘米的速度由点向点运动,设运动时间为秒 .
(1)用含的代数式表示的长度.
(2)若点、的运动速度相等,经过秒后,与是否全等,请说明理由;
(3)若点、的运动速度不相等,当点的运动速度为多少时,能够使与全等?
【答案】(1)
(2)是,理由见解析
(3)当 时,能够使与全等
【分析】此题主要考查了动点问题和全等三角形的判定,
(1)直接根据时间和速度表示的长;
(2)根据证明即可;
(3)因为点的运动速度不相等,所以,那么只能与相等,则,得,解出即可.
【详解】(1)解:由题意得:,
则;
(2)解:,理由如下:
当时,由题意得:,,
∴,
∵,
∴,
∵是的中点,
∴,
∴,
在和中,
∵,
∴;
(3)解:∵点的运动速度不相等,
∴,
当与全等,且,
∴,
∵,
∴ ,
∴ ,
∴当 时,能够使与全等.
【变式7-1】(23-24八年级·广东潮州·期中)如图,在矩形中,,点E在线段上,且,动点P在线段上,从点A出发以的速度向点B运动,同时点Q在线段上.以的速度由点B向点C运动,当与全等时,v的值为( )
A.2 B.4 C.4或 D.2或
【答案】D
【分析】本题考查了矩形的性质及全等三角形的判定与性质等知识点,数形结合、分类讨论并熟练掌握相关性质及定理是解题的关键.
当与全等时,有两种情况:①当时,,②当时,,分别按照全等三角形的性质及行程问题的基本数量关系求解即可.
【详解】解:当与全等时,有两种情况:
①当时,,
,,
,,
;
动点在线段上,从点出发以的速度向点运动,
点和点的运动时间为:,
∴;
②当时,,
,,
,,
,
,
综上,v的值为2或.
故选:D.
【变式7-2】(23-24八年级·湖南郴州·期中)如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为 .
【答案】或
【分析】本题主要考查正方形的性质,三角形全等的判定与性质,关键是要考虑到点P的两种情况,牢记三角形全等的性质是解本题的关键.根据由点P的运动情况可知,和全等分以下两种情况:①当点P在上运动时,②当点P在上运动时,利用三角形全等的性质建立关于等式求解,即可解题.
【详解】解:由点P的运动情况可知,和全等分以下两种情况:
①当点P在上运动时,
四边形为正方形,,
,,
,
要和全等,
即,
,
,解得;
②当点P在上运动时,
要和全等,
即,
,
,解得;
综上所述,t的值为或.
故答案为:或.
【变式7-3】(23-24八年级·河南郑州·期末)如图,在中,为高线,.点为上一点,,连接,交于点,若.
(1)猜想线段与的位置关系,并证明;
(2)若动点从点出发沿射线以每秒6个单位长度的速度运动,运动的时间为秒.
①当点在线段上时,是否存在的值,使得的面积为27?若存在,请求出的值;若不存在,请说明理由;
②动点从点出发沿线段以每秒2个单位长度的速度向终点运动,,两点同时出发,当点到达点时,,两点同时停止运动.设运动时间为秒,点是直线上一点,且,当与全等时,请直接写出的值.
【答案】(1),证明见解析
(2)①存在t的值,理由见解析,;②t的值为或
【分析】本题是三角形综合题,考查了全等三角形的判定和性质,直角三角形的性质,利用分类讨论思想解决问题是解题的关键.
(1)由全等三角形的性质可得,由余角的性质可得,即可求解;
(2)①由全等三角形的性质可得,由三角形的面积公式可求解;
②分两种情况讨论,由全等三角形的判定列出等式,即可求解.
【详解】(1)解:,理由如下:
在中,为高,
,
又,
,
,,
,
;
(2)解:①存在的值,使得的面积为27,理由如下:
,,
,
,
,,
由(1)可知,,
,
在线段上,
,
解得:;
②,
,
、当点在线段延长线上时,如图3,
,
,
,
当时,,
此时,,
解得:;
、当点在线段上时,如图4,
,
,
,
当时,,
此时,,
解得:;
综上所述,当与全等时,的值为或.
【题型8 全等三角形的应用】
【例8】(23-24八年级·贵州铜仁·期末)某同学根据数学知识原理制作了如图所示的一个测量工具----拐尺,其中O为AB的中点,CA⊥AB,BD⊥AB,CA=BD,现要测量一透明隔离房间的深度,如何使用此测量工具,说明理由.
【答案】理由见解析.
【分析】使AC与房间内壁在一条直线上,且C与一端点接触,然后人在BD的延长线上移动至F,使F、O、E三点正好在一条直线上,记下F点,这时量出DF长,即为房间深度CE.通过证△EAO≌△FBO,可得BF=AE,则BF-BD=AE-AC,即DF=CE.
【详解】解:如图,使AC与房间内壁在一条直线上,且C与一端点接触,然后人在BD的延长线上移动至F,使F,O,E三点正好在一条直线上,记下F点,这时量出DF长,即为房间深度CE.理由如下:由∠A=∠B=90°,OA=OB,∠EOA=∠FOB,
∴△EAO≌△FBO,
得BF=AE,
则BF-BD=AE-AC,即DF=CE.
【点睛】本题考核知识点:全等三角形判定的应用. 解题关键点:构造全等三角形.
【变式8-1】(23-24八年级·陕西西安·期中)如图,小刚站在河边的点A处,在河对面(小刚的正北方向)的点B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了20步到达一棵树C处,接着再向前走了20步到达D处,然后他左转直行,从点D处开始计步,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他恰好走了74步,并且小刚一步大约0.5米.由此小刚估计出了在点A处时他与电线塔的距离,请问他的做法是否合理?若合理,请求出在点A处时他与电线塔的距离;若不合理,请说明理由.
【答案】合理,37米
【分析】本题考查全等三角形的应用,根据可得出,由该全等三角形的性质,故可求解.
【详解】解:合理,理由如下:
根据题意,得.
在和中,
∴.
∴.
又∵小刚走完用了74步,一步大约0.5米,
∴(米).
∴小刚在点A处时他与电线塔的距离为37米.
【变式8-2】(23-24八年级·陕西西安·期末)小乐与朋友们周末去游乐园乘坐海盗船游玩,想了解海盗船摆动到最高点位置时的高度.如图,当静止时海盗船位于铅垂线上,转轴到地面的距离,在乘坐的过程中,当海盗船静止在点处时,,此时测得点到铅垂线的距离,当船头从处摆动到处时发现船头处在最高位置处,此时,.求点到地面的距离.
【答案】
【分析】本题主要考查了全等三角形的判定以及性质,过点作于点F,利用证明,由全等三角形的性质可得出,进而可求出的值,即点到地面的距离.
【详解】解:如图,过点作于点F,
∵,,
∴,
∴,
∴,
∴,
∴,
∴,
∴即点到地面的距离为.
【变式8-3】(23-24八年级·河南郑州·期末)茗阳阁位于河南省信阳市浉河区茶韵路一号,建成于2007年4月29日,是信阳新建的城市文化与形象的代表建筑之一.设两点分别为茗阳阁底座的两端(其中两点均在地面上).因为两点间的实际距离无法直接测量,某学习小组分别设计出了如下两种方案:甲:如图1,在平地上取一个可以直接到达点的点O,连接并延长到点C,连接并延长到点D,使,连接,测出的长即可.乙:如图2,先确定直线,过点B作,在点D处用测角仪确定,射线交直线于点C,最后测量的长即可得线段的长.
(1)请用所学知识论证甲、乙两种方案的合理性;
(2)如果让你参与测量,你会选择哪一种方案?请说明理由.
【答案】(1)见解析
(2)见解析
【分析】本题主要考查了全等三角形的应用.熟练掌握全等三角形的判定定理是解决问题的关键.
(1)甲方案作出的是全等三角形,然后根据全等三角形对应边相等测量的,所以是可行的;乙方案作出的也是全等三角形,然后根据全等三角形对应边相等测量的,所以也是可行的;
(2)选甲方案,使用工具操作容易;乙方案使用工具操作相对不容易,A,B间可视性未知.
【详解】(1)甲方案:
在与中,
,
∴,
∴,
乙方案
∵,
∴,
在与中,
,
∴,
∴.
(2)选甲种方案,理由:使用工具简单,只需要测量长度的刻度尺,容易操作;乙种方案使用工具需要测量长度的刻度尺和测量角度的测角仪,不容易操作,A,B间是否具备可视性.
21世纪教育网(www.21cnjy.com)
【人教版】
【题型1 添加条件使三角形全等】 1
【题型2 确定全等三角形的对数】 2
【题型3 网格中确定全等三角形】 3
【题型4 灵活选用判定方法证明全等】 5
【题型5 多次证全等求解或证明结论】 6
【题型6 由全等三角形的判定与性质确定线段之间的关系】 7
【题型7 全等三角形的动态问题】 9
【题型8 全等三角形的应用】 10
知识点:全等三角形的判定
判定两个三角形全等常用的思路方法如下:
【题型1 添加条件使三角形全等】
【例1】(23-24八年级·山东东营·期中)如图,在和中,点B、D、C在同一直线上,已知,,添加以下条件后,仍不能判定的是( )
A. B. C. D.
【变式1-1】(23-24八年级·河南信阳·期中)在和中,,有下列条件:①;②;③;④;⑤.请你从中选择两个条件: ,使,你判断它们全等的根据是 .
【变式1-2】(23-24八年级·江苏徐州·期中)如图,已知,,要使,则需要添加的条件是 .(写一个即可)
【变式1-3】(23-24八年级·湖北襄阳·期末)如图,点B、E、C、F四点在一条直线上,∠A=∠D,AB//DE,老师说:再添加一个条件就可以使△ABC≌△DEF.下面是课堂上三个同学的发言,甲说:添加AB=DE;乙说:添加AC//DF;丙说:添加BE=CF.
(1)甲、乙、丙三个同学说法正确的是________;
(2)请你从正确的说法中选择一种,给出你的证明.
【题型2 确定全等三角形的对数】
【例2】(23-24八年级·河南信阳·期中)如图,在中,,连接相交于点,连接,则图中共有全等三角形( )
A.5对 B.4对 C.3对 D.2对
【变式2-1】(23-24八年级·河南南阳·期末)如图,AB=AC,BD⊥AC于D,CE⊥AB于E.BD与CE交于O,连接AO,则图中共有全等的三角形的对数为( )
A.1对 B.2对 C.3对 D.4对
【变式2-2】(23-24八年级·广东深圳·期中)如图,,,,图中全等的三角形的对数是( )
A.4 B.5 C.6 D.7
【变式2-3】(23-24八年级·重庆渝北·期末)如图(1),已知,为的角平分线上一点,连接,;如图(2),已知,,为的角平分线上两点,连接,,,;如图(3),已知,,,为的角平分线上三点,连接,,,,,;,依此规律,第6个图形中有全等三角形的对数是( )
A. B. C. D.
【题型3 网格中确定全等三角形】
【例3】(23-24八年级·湖北武汉·阶段练习)如图,方格中的3个顶点分别在正万形的顶点(格点上),这样的三角形叫格点三角形,图中与(不含)全等的格点三角形共有( )个
A.4 B.5 C.8 D.7
【变式3-1】(23-24八年级·湖北武汉·阶段练习)如图是的正方形网格,的顶点都在小正方形的顶点上,像这样的三角形叫做格点三角形,画与只有一条公共边且全等的格点三角形,在该网格中这样的格点三角形(不与重合)最多可以画出 个.
【变式3-2】(23-24八年级·河北廊坊·期末)在方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形,解决下列问题.
(1)如图1,以点D和点E为两个顶点作格点三角形,使所作的格点三角形与△ABC全等,那么这样的格点三角形最多可以画出 个;
(2)如图2,∠1+∠2= .
【变式3-3】(23-24八年级·宁夏吴忠·期中)如图,是格点三角形(顶点在网格线的交点上),请在下列每个方格纸上按要求画一个与全等的格点三角形.
(1)在图①中所画三角形与有一条公共边;
(2)在图②中所画三角形与有一个公共角;
(3)在图③中所画三角形与△有且只有一个公共顶点.
【题型4 灵活选用判定方法证明全等】
【例4】(23-24八年级·山东青岛·期中)如图, ,,.求证:.
以下是合作小组三名同学关于此题的讨论:
小丽说:“我可以根据全等三角形的判定定理‘’证明两个三角形全等,从而得到.”
小颖说:“我可以根据直角三角形全等的判定定理‘’证明两个三角形全等,从而得到.”
小雨说:“我可以根据三角形的面积相等,来证明.”
看了他们的讨论,你一定也有了自己的主意,请写出你的证明.
【变式4-1】(23-24八年级·河南郑州·期末)下列所给的四组条件中,能作出唯一三角形的是( )
A. B.,,
C.,, D.,,
【变式4-2】(23-24八年级·河南郑州·期末)已知的三个内角三条边长如图所示,则甲、乙、丙三个三角形中,和全等的图形是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
【变式4-3】(23-24八年级·河北保定·期末)(1)阅读下题及证明过程
已知:如图,是的边上一点,是上一点,,.
求证:.
证明:在和中,
因为,,,
所以………………第一步
所以………………第二步
上面的证明过程是否正确?若正确,请写出每一步推理的依据;若不正确,请指出错在哪一步,并写出你认为正确的证明过程.
(2)如果两个锐角三角形的两组边分别相等,且其中一组等边的对角相等,那么这两个三角形全等吗?请说明理由.
【题型5 多次证全等求解或证明结论】
【例5】(23-24八年级·黑龙江哈尔滨·期末)已知:是的角平分线,且
(1)如图1,求证:;
(2)如图2,,点E在AD上,连接并延长交于点F,交的延长线于点G,且,连接.
①求证:;
②若,且,求AC的长.
【变式5-1】(23-24八年级·河南洛阳·期末)已知:如图,,,与相交于点,连接.
证明:
(1);
(2)平分.
【变式5-2】(23-24八年级·广西百色·期末)如图,已知,于点D,于点B,.
(1)求证:;
(2)连接交于点O,试判断与之间的数量关系,并说明理由.
【变式5-3】(23-24八年级·重庆·期末)如图1,在等边三角形中,点D在上,点E在上,,交于点F,于点G,延长交于点H,.
(1)求证:.
(2)如图2,连接,若,求证:点F是的中点.
【题型6 由全等三角形的判定与性质确定线段之间的关系】
【例6】(23-24八年级·江西南昌·期末)如图,是的角平分线.
(1)若,求证:;
(2)当时,与的数量关系如何?说说你的理由.
【变式6-1】(23-24八年级·广东潮州·阶段练习)在中,,,直线经过点,且于,于.
(1)当直线绕点旋转到图的位置时,求证:
①;
②;
(2)当直线绕点旋转到图的位置时,,,求线段的长.
【变式6-2】(23-24八年级·重庆·期末)如图,在中,,,过点B作,且,点B作交于点F,连接.
(1)如图1,若,且,求的度数;
(2)如图2,若,求证:.
【变式6-3】(23-24八年级·重庆·期末)在中,和的角平分线相交于点.
(1)若,求的度数;
(2)延长至点,过点作的平行线交于点,若,求证:.
【题型7 全等三角形的动态问题】
【例7】(23-24八年级·湖南郴州·期中)如图,已知中,,厘米,厘米,点为的中点,如果点在线段上以每秒厘米的速度由点向点运动,同时,点在线段上以每秒厘米的速度由点向点运动,设运动时间为秒 .
(1)用含的代数式表示的长度.
(2)若点、的运动速度相等,经过秒后,与是否全等,请说明理由;
(3)若点、的运动速度不相等,当点的运动速度为多少时,能够使与全等?
【变式7-1】(23-24八年级·广东潮州·期中)如图,在矩形中,,点E在线段上,且,动点P在线段上,从点A出发以的速度向点B运动,同时点Q在线段上.以的速度由点B向点C运动,当与全等时,v的值为( )
A.2 B.4 C.4或 D.2或
【变式7-2】(23-24八年级·湖南郴州·期中)如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为 .
【变式7-3】(23-24八年级·河南郑州·期末)如图,在中,为高线,.点为上一点,,连接,交于点,若.
(1)猜想线段与的位置关系,并证明;
(2)若动点从点出发沿射线以每秒6个单位长度的速度运动,运动的时间为秒.
①当点在线段上时,是否存在的值,使得的面积为27?若存在,请求出的值;若不存在,请说明理由;
②动点从点出发沿线段以每秒2个单位长度的速度向终点运动,,两点同时出发,当点到达点时,,两点同时停止运动.设运动时间为秒,点是直线上一点,且,当与全等时,请直接写出的值.
【题型8 全等三角形的应用】
【例8】(23-24八年级·贵州铜仁·期末)某同学根据数学知识原理制作了如图所示的一个测量工具----拐尺,其中O为AB的中点,CA⊥AB,BD⊥AB,CA=BD,现要测量一透明隔离房间的深度,如何使用此测量工具,说明理由.
【变式8-1】(23-24八年级·陕西西安·期中)如图,小刚站在河边的点A处,在河对面(小刚的正北方向)的点B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了20步到达一棵树C处,接着再向前走了20步到达D处,然后他左转直行,从点D处开始计步,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他恰好走了74步,并且小刚一步大约0.5米.由此小刚估计出了在点A处时他与电线塔的距离,请问他的做法是否合理?若合理,请求出在点A处时他与电线塔的距离;若不合理,请说明理由.
【变式8-2】(23-24八年级·陕西西安·期末)小乐与朋友们周末去游乐园乘坐海盗船游玩,想了解海盗船摆动到最高点位置时的高度.如图,当静止时海盗船位于铅垂线上,转轴到地面的距离,在乘坐的过程中,当海盗船静止在点处时,,此时测得点到铅垂线的距离,当船头从处摆动到处时发现船头处在最高位置处,此时,.求点到地面的距离.
【变式8-3】(23-24八年级·河南郑州·期末)茗阳阁位于河南省信阳市浉河区茶韵路一号,建成于2007年4月29日,是信阳新建的城市文化与形象的代表建筑之一.设两点分别为茗阳阁底座的两端(其中两点均在地面上).因为两点间的实际距离无法直接测量,某学习小组分别设计出了如下两种方案:甲:如图1,在平地上取一个可以直接到达点的点O,连接并延长到点C,连接并延长到点D,使,连接,测出的长即可.乙:如图2,先确定直线,过点B作,在点D处用测角仪确定,射线交直线于点C,最后测量的长即可得线段的长.
(1)请用所学知识论证甲、乙两种方案的合理性;
(2)如果让你参与测量,你会选择哪一种方案?请说明理由.21世纪教育网(www.21cnjy.com)
专题12.3 三角形全等的判定(探索篇)【八大题型】
【人教版】
【题型1 添加条件使三角形全等】 2
【题型2 确定全等三角形的对数】 5
【题型3 网格中确定全等三角形】 8
【题型4 灵活选用判定方法证明全等】 12
【题型5 多次证全等求解或证明结论】 18
【题型6 由全等三角形的判定与性质确定线段之间的关系】 24
【题型7 全等三角形的动态问题】 31
【题型8 全等三角形的应用】 37
知识点:全等三角形的判定
判定两个三角形全等常用的思路方法如下:
【题型1 添加条件使三角形全等】
【例1】(23-24八年级·山东东营·期中)如图,在和中,点B、D、C在同一直线上,已知,,添加以下条件后,仍不能判定的是( )
A. B. C. D.
【答案】D
【分析】本题考查了全等三角形的判定.将各个选项依次代入题目当中,再根据全等三角形的判定方法依次判断即可.一般三角形全等的判定方法有、、、,注意没有.熟练掌握全等三角形的判定方法是解题的关键.
【详解】解:A、若添加,则可根据证明,故A选项不符合题意;
B、若添加,则可得,则可根据证明,故B选项不符合题意;
C、若添加,则可根据证明,故C选项不符合题意;
D、若添加,则成了,不能证明,故D选项符合题意.
故选:D
【变式1-1】(23-24八年级·河南信阳·期中)在和中,,有下列条件:①;②;③;④;⑤.请你从中选择两个条件: ,使,你判断它们全等的根据是 .
【答案】 ②③(答案不唯一)
【分析】本题考查三角形全等的判定方法,根据四个选项所给条件结合判定两个三角形全等的方法分别进行分析即可.
【详解】解:∵,添加②;③;可利用判定;
添加③;④,可利用判定;
添加⑤;③,可利用判定;
故答案为:答案不唯一,如②③;SAS.
【变式1-2】(23-24八年级·江苏徐州·期中)如图,已知,,要使,则需要添加的条件是 .(写一个即可)
【答案】或或(写一个即可)
【分析】本题考查全等三角形的判定,判定两个三角形全等的一般方法有:、、、、.由,可得,再根据题干中的条件,可添加角相等或边相等即可.
【详解】解:添加,
,
,
又 ,,
,
添加,
,
,
又 ,,
,
添加,
,
,
又 ,,
,
故答案为:或或(写一个即可).
【变式1-3】(23-24八年级·湖北襄阳·期末)如图,点B、E、C、F四点在一条直线上,∠A=∠D,AB//DE,老师说:再添加一个条件就可以使△ABC≌△DEF.下面是课堂上三个同学的发言,甲说:添加AB=DE;乙说:添加AC//DF;丙说:添加BE=CF.
(1)甲、乙、丙三个同学说法正确的是________;
(2)请你从正确的说法中选择一种,给出你的证明.
【答案】(1)甲、丙;(2)见详解
【分析】(1)根据平行线的性质,由AB∥DE可得∠B=∠DEC,再加上条件∠A=∠D,只需要添加一个能得出对应边相等的条件,即可证明两个三角形全等,添加AC//DF不能证明△ABC≌△DEF;
(2)添加AB=DE,再由条件AB∥DE可得∠B=∠DEC,然后再利用ASA判定△ABC≌△DEF即可.
【详解】(1)解:∵AB//DE,
∴∠B=∠DEC,
又∵∠A=∠D,
∴添加AB=DE,可得△ABC≌△DEF(ASA);添加BE=CF,可得BC=EF,可得△ABC≌△DEF(AAS)
∴说法正确的是:甲、丙,
故答案为:甲、丙;
(2)选“甲”,理由如下:
证明:∵AB∥DE,
∴∠B=∠DEC,
在△ABC和△DEF中
∴△ABC≌△DEF(ASA).
【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
【题型2 确定全等三角形的对数】
【例2】(23-24八年级·河南信阳·期中)如图,在中,,连接相交于点,连接,则图中共有全等三角形( )
A.5对 B.4对 C.3对 D.2对
【答案】A
【分析】本题考查全等三角形的判定,根据题中条件,数形结合,利用两个三角形全等的判定定理逐个验证即可得到答案,熟练掌握两个三角形全等的判定定理是解决问题的关键.
【详解】解:①由,,根据可得;
②由可得,
由可得,则由,,,根据可得;
③由可得,则由,,根据可得;
④由可得,则由,,根据可得;
⑤由可得;由可得;;根据可得;
综上所述,图中共有全等三角形5对,
故选:A.
【变式2-1】(23-24八年级·河南南阳·期末)如图,AB=AC,BD⊥AC于D,CE⊥AB于E.BD与CE交于O,连接AO,则图中共有全等的三角形的对数为( )
A.1对 B.2对 C.3对 D.4对
【答案】D
【分析】根据AB=AC,BD⊥AC于D,CE⊥AB于E,∠CAE=∠BAD,可证明△CAE≌△BAD,得出AD=AE,∠C=∠B,根据AAS可证明△DCO≌△EBO,得出CO=BO,利用SSS证得△ACO≌△ABO,利用HL证得△DAO≌△EAO,由此得出共有全等的三角形的对数为4对.
【详解】解:由题意可得△CAE≌△BAD,△DCO≌△EBO,△ACO≌△ABO,△DAO≌△EAO共4对三角形全等.
故选:D.
【点睛】本题考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
【变式2-2】(23-24八年级·广东深圳·期中)如图,,,,图中全等的三角形的对数是( )
A.4 B.5 C.6 D.7
【答案】C
【分析】根据全等三角形得判定定理,依次证明三角形全等,即可求解.
【详解】解:,,
,,
在与中,
,
,
,,
在与中,
,
,
,
,
,
,
在与中,
,
同理可得,
,
,
即6对全等三角形.
故选:C.
【点睛】本题考查了全等三角形的判定,能正确根据定理进行推论是解题的关键.
【变式2-3】(23-24八年级·重庆渝北·期末)如图(1),已知,为的角平分线上一点,连接,;如图(2),已知,,为的角平分线上两点,连接,,,;如图(3),已知,,,为的角平分线上三点,连接,,,,,;,依此规律,第6个图形中有全等三角形的对数是( )
A. B. C. D.
【答案】A
【分析】设第个图形中有为正整数)个全等三角形,根据各图形中全等三角形对数的变化可找出变化规律“为正整数)”,再代入即可求出结论.
【详解】解:设第个图形中有为正整数)个全等三角形.
图(1),在和中,
,
,
;
同理,可得:,,,,
为正整数),
.
故选:A.
【点睛】本题考查了全等三角形的判定以及规律型:图形的变化类,根据各图形中全等三角形对数的变化,找出变化规律“为正整数)”是解题的关键.
【题型3 网格中确定全等三角形】
【例3】(23-24八年级·湖北武汉·阶段练习)如图,方格中的3个顶点分别在正万形的顶点(格点上),这样的三角形叫格点三角形,图中与(不含)全等的格点三角形共有( )个
A.4 B.5 C.8 D.7
【答案】D
【分析】
本题考查全等三角形的判定,根据全等三角形的判定方法,结合网格的特点,画出图形,即可得出结果.
【详解】解:如图所示以正方形一边为三角形的边都可作两个全等的三角形,
所以共有8个全等三角形,除去外有7个与全等的三角形.即:
故选D.
【变式3-1】(23-24八年级·湖北武汉·阶段练习)如图是的正方形网格,的顶点都在小正方形的顶点上,像这样的三角形叫做格点三角形,画与只有一条公共边且全等的格点三角形,在该网格中这样的格点三角形(不与重合)最多可以画出 个.
【答案】
【分析】本题考查了全等三角形、格点三角形的定义,可以以为公共边和以为公共边分别画出个三角形,以为公共边不可以画出三角形,即可得出答案,采用数形结合的思想是解此题的关键.
【详解】解:如图所示:
,
以为公共边可以画出、、三个三角形,
以为公共边可以画出、、三个三角形,
故可以画出个,
故答案为:.
【变式3-2】(23-24八年级·河北廊坊·期末)在方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形,解决下列问题.
(1)如图1,以点D和点E为两个顶点作格点三角形,使所作的格点三角形与△ABC全等,那么这样的格点三角形最多可以画出 个;
(2)如图2,∠1+∠2= .
【答案】 4 45°/45度
【分析】(1)观察图形可知:DE与AC是对应边,B点的对应点在DE上方两个,在DE下方两个共有4个满足要求的点,也就有四个全等三角形;
(2)由图可知∠1=∠3,∠2+∠3=45°,从而可得结论.
【详解】解:(1)根据题意,运用SSS可得与△ABC全等的三角形有4个,线段DE的上方有两个点,下方也有两个点.
故答案为:4.
(2)由图可知△ABC≌△EDC,
∴∠1=∠3,
而∠2+∠3=45°,
∴∠1+∠2=45°,
故答案为:45°.
【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL,做题时要做到不重不漏.
【变式3-3】(23-24八年级·宁夏吴忠·期中)如图,是格点三角形(顶点在网格线的交点上),请在下列每个方格纸上按要求画一个与全等的格点三角形.
(1)在图①中所画三角形与有一条公共边;
(2)在图②中所画三角形与有一个公共角;
(3)在图③中所画三角形与△有且只有一个公共顶点.
【答案】(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据题意以及网格的特点根据轴对称画出图形即可;
(2)根据题意以及网格的特点根据轴对称画出图形即可;
(3)根据题意以及网格的特点画出图形即可.
【详解】(1)如图①所示,△ABD即为所求;
(2)如图②所示,△DEC即为所求;
(3)如图③所示,△AED即为所求,
【点睛】本题考查了作图-应用与设计作图、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题.
【题型4 灵活选用判定方法证明全等】
【例4】(23-24八年级·山东青岛·期中)如图, ,,.求证:.
以下是合作小组三名同学关于此题的讨论:
小丽说:“我可以根据全等三角形的判定定理‘’证明两个三角形全等,从而得到.”
小颖说:“我可以根据直角三角形全等的判定定理‘’证明两个三角形全等,从而得到.”
小雨说:“我可以根据三角形的面积相等,来证明.”
看了他们的讨论,你一定也有了自己的主意,请写出你的证明.
【答案】见解析
【分析】本题目考查了三角形全等的判定方法,解题关键是熟练掌握三角形全等的判定定理是解题的关键;
①根据垂线的知识可得,在结合证明,最后根据全等三角形的性质得出结论;②连接,根据直角三角形的,证明,即可得出结论;③连接,证明,可得,再结合三角形面积计算方法即可得出结论;④连接,证明,得,,在利用证明,得出结论.
【详解】小丽方法:
,,
.
在和中,
,.
,即.
小颖方法:
连接.
,,,
.
在和中,
.
.
小雨方法:
连接.
,
.
在和中,
,
,
.即.
又 ,,
,
,
.
方法4:连接,
,,
.
在和中,
,,
,
在和中,
,
.
【变式4-1】(23-24八年级·河南郑州·期末)下列所给的四组条件中,能作出唯一三角形的是( )
A. B.,,
C.,, D.,,
【答案】D
【分析】本题主要考查了构成三角形的条件.熟练掌握三角形全等的判定方法,三角形三边关系,是解决问题的关键.
根据三角形三边的关系对B进行判断;根据全等三角形的判定方法对A、C、D进行判断.
【详解】A.,
不符合三角形全等判定条件,不能作出唯一三角形;
B.,,,
这里,不符合三角形三边关系,不能作出三角形;
C.,,,
两边和其中一边的对角对应相等的两个三角形不一定全等,不能作出唯一三角形;
D.,,,
两边及夹角对应相等的两个三角形全等,能作出唯一三角形.
故选:D.
【变式4-2】(23-24八年级·河南郑州·期末)已知的三个内角三条边长如图所示,则甲、乙、丙三个三角形中,和全等的图形是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
【答案】B
【分析】本题考查全等三角形的判定方法,掌握三角形判定方法是解题的关键.
根据三角形判定方法判断即可解答.
【详解】解:甲与不符合两边对应相等,且夹角相等,
∴甲和已知三角形不全等;
乙与符合两边对应相等,且夹角相等,
∴根据可判定乙和与全等;
丙与符合两角对应相等,且其中一角的对边相等,
∴根据可判定丙和与全等.
故选:B.
【变式4-3】(23-24八年级·河北保定·期末)(1)阅读下题及证明过程
已知:如图,是的边上一点,是上一点,,.
求证:.
证明:在和中,
因为,,,
所以………………第一步
所以………………第二步
上面的证明过程是否正确?若正确,请写出每一步推理的依据;若不正确,请指出错在哪一步,并写出你认为正确的证明过程.
(2)如果两个锐角三角形的两组边分别相等,且其中一组等边的对角相等,那么这两个三角形全等吗?请说明理由.
【答案】(1)不正确;错在第一步,详见解析;(2)全等,详见解析
【分析】本题考查了全等三角形的判定与性质,等腰三角形的判定与性质,熟练掌握全等三角形的判定与性质是解答本题的关键.
(1)根据两边及其中一边的对角对应相等的两个三角形不一定全等,可知第一步错误,证明时先根据等腰三角形的性质及判定,可逐步推得,再根据“边边边”判定三角形全等即可;
(2)先写出已知,求证与证明,“已知,在锐角三角形和锐角三角形中,,,.求证:.”过点A作于点D,过点作于点,先根据“角角边”证明,得到,再根据“”定理证明,得到,最后由“ 角角边”即可证得结果.
【详解】(1)不正确;错在第一步.
证明:在△BEC中,∵,
∴,
∵,
,
,
在和中,
,
;
(2)全等.理由如下:
已知:如图,在锐角三角形和锐角三角形中,
,,.
求证:.
证明:过点A作于点D,过点作于点,
,
在和中,
,
,
,
在和中,
,
,
,
在和中,
,
.
【题型5 多次证全等求解或证明结论】
【例5】(23-24八年级·黑龙江哈尔滨·期末)已知:是的角平分线,且
(1)如图1,求证:;
(2)如图2,,点E在AD上,连接并延长交于点F,交的延长线于点G,且,连接.
①求证:;
②若,且,求AC的长.
【答案】(1)见解析
(2)①证明见解析②6
【分析】本题主要考查了全等三角形的性质与判定以及角平分线的定义.
(1)用证明,即得;
(2)①证明可得,再用证明,即得;②过作于,由,可得,,而,,即得,根据,可求.
【详解】(1)证明:是的角平分线,
,
,
,
在和中,
,
,
;
(2)①,,,
,
,
在和中,
,
,
,
在和中,
,
,
;
②过作于,如图:
由①知:,
,
,
,
由①知:,
,
,
,
,
∴.
【变式5-1】(23-24八年级·河南洛阳·期末)已知:如图,,,与相交于点,连接.
证明:
(1);
(2)平分.
【答案】(1)见解析
(2)见解析
【分析】本题考查全等三角形的知识,解题的关键是掌握全等三角形的判定和性质,等边对等角,角平分线的性质,即可.
(1)根据,,得,推出,则,根据,则,则,即可得;
(2)由(1)得,,,推出,则,即可.
【详解】(1)证明如下:
∵,,
∴,
∴,
在和,
,
∴,
∴,
∵,
∴,
∴,
∴.
(2)证明:∵,
∴,
∴,
即平分.
【变式5-2】(23-24八年级·广西百色·期末)如图,已知,于点D,于点B,.
(1)求证:;
(2)连接交于点O,试判断与之间的数量关系,并说明理由.
【答案】(1)见解析
(2),见解析
【分析】本题考查了全等三角形的判定与性质,熟练掌握相关判定定理是解决本题的关键.
(1)根据证明,再根据全等三角形的性质即可得;
(2)根据证明,再根据全等三角形的性质即可得.
【详解】(1)证明:如图所示,
∵,
∴
在和中,
,
∴
∴;
(2)解:
理由如下:
如图,
在和中,
,
∴,
∴.
【变式5-3】(23-24八年级·重庆·期末)如图1,在等边三角形中,点D在上,点E在上,,交于点F,于点G,延长交于点H,.
(1)求证:.
(2)如图2,连接,若,求证:点F是的中点.
【答案】(1)见解析
(2)见解析
【分析】本题考查了全等三角形的判定和性质,等边三角形的性质,添加恰当辅助线构造全等三角形是解题的关键.
(1)由可证,可得;
(2)延长交于点Q,由可证,可得,由可证,可得,可得结论.
【详解】(1)∵是等边三角形,
∴,,
∵,,
∴,,
∴,
∴,
在和中,
,
∴,
∴;
(2)如图,延长交于点Q,
∵,,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∴点F是的中点.
【题型6 由全等三角形的判定与性质确定线段之间的关系】
【例6】(23-24八年级·江西南昌·期末)如图,是的角平分线.
(1)若,求证:;
(2)当时,与的数量关系如何?说说你的理由.
【答案】(1)见解析
(2),理由见解析
【分析】(1)延长至E,使,连接,运用证明,可得结论;
(2)在的延长线上取点F,使,连接,根据推导得到结论.
【详解】(1)证明:延长至E,使,连接.
∵,
∴.
∵平分,
∴.
在与中,
,
∴.
∴.
∵,
∴
∵,
∴.
(2)解:.
理由:在的延长线上取点F,使,连接.
∴,
又∵,
∴.
∵,
∴.
∵是的角平分线,
∴,
在与中,
,
∴.
∴.
【点睛】本题考查全等三角形的判定和性质,角平分线的定义,三角形外角性质,等腰三角形的判定和性质.正确的作出辅助线是解题关键.
【变式6-1】(23-24八年级·广东潮州·阶段练习)在中,,,直线经过点,且于,于.
(1)当直线绕点旋转到图的位置时,求证:
①;
②;
(2)当直线绕点旋转到图的位置时,,,求线段的长.
【答案】(1)见解析,见解析;
(2).
【分析】(1)由已知推出,因为,,推出,根据即可得到答案;
由得到,,即可求出答案;
()与()证法类似可证出,能推出,得到,,代入已知即可得到答案,
本题考查了全等三角形的性质和判定,同角的余角相等,垂直的定义,熟练掌握知识点的应用是解题的关键.
【详解】(1)证明:∵,,
∴,
∵,
∴,,
∴,
在和中,
,
∴;
证明:由()知:,
∴,,
∵,
∴;
(2)证明:∵,,
∴,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,,
∴.
【变式6-2】(23-24八年级·重庆·期末)如图,在中,,,过点B作,且,点B作交于点F,连接.
(1)如图1,若,且,求的度数;
(2)如图2,若,求证:.
【答案】(1)
(2)见解析
【分析】本题考查等腰三角形的性质、全等三角形的判定与性质、三角形的外角性质、平行线的性质等知识,熟练运用全等三角形的性质探究线段间的关系是解答的关键.
(1)先根据平行线的性质得到,,再根据等腰三角形的性质求得,,进而利用三角形的外角性质求解即可;
(2)先求得,在上截取,连接,分别证明和得到,进而可得结论.
【详解】(1)解:∵,,,
∴,,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
(2)证明:∵,,
∴,
∵,
∴,
如图,在上截取,连接,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,,
∴,
在和中,
,
∴,
∴,
∴,
∴.
【变式6-3】(23-24八年级·重庆·期末)在中,和的角平分线相交于点.
(1)若,求的度数;
(2)延长至点,过点作的平行线交于点,若,求证:.
【答案】(1);
(2)证明见解析.
【分析】()根据角平分线的定义,三角形内角和定理即可求解;
()在上截取,连接,证明,,再根据性质即可求证;
本题考查了角平分线的定义,三角形内角和定理,三角形全等的性质与判定,平行线的性质,熟练掌握知识点的应用是解题的关键.
【详解】(1)解:∵,
∴,
∵和的角平分线相交于点,
∴,,
∴,
∴;
(2)证明:如图,在上截取,连接,
∵平分,
∴垂直平分,
∴,
∵,
∴,
又∵,
∴,
∴,
∴,
又∵,
∴,
∵平分,
∴,
∴,
∴,
∴,
∵,
∴.
【题型7 全等三角形的动态问题】
【例7】(23-24八年级·湖南郴州·期中)如图,已知中,,厘米,厘米,点为的中点,如果点在线段上以每秒厘米的速度由点向点运动,同时,点在线段上以每秒厘米的速度由点向点运动,设运动时间为秒 .
(1)用含的代数式表示的长度.
(2)若点、的运动速度相等,经过秒后,与是否全等,请说明理由;
(3)若点、的运动速度不相等,当点的运动速度为多少时,能够使与全等?
【答案】(1)
(2)是,理由见解析
(3)当 时,能够使与全等
【分析】此题主要考查了动点问题和全等三角形的判定,
(1)直接根据时间和速度表示的长;
(2)根据证明即可;
(3)因为点的运动速度不相等,所以,那么只能与相等,则,得,解出即可.
【详解】(1)解:由题意得:,
则;
(2)解:,理由如下:
当时,由题意得:,,
∴,
∵,
∴,
∵是的中点,
∴,
∴,
在和中,
∵,
∴;
(3)解:∵点的运动速度不相等,
∴,
当与全等,且,
∴,
∵,
∴ ,
∴ ,
∴当 时,能够使与全等.
【变式7-1】(23-24八年级·广东潮州·期中)如图,在矩形中,,点E在线段上,且,动点P在线段上,从点A出发以的速度向点B运动,同时点Q在线段上.以的速度由点B向点C运动,当与全等时,v的值为( )
A.2 B.4 C.4或 D.2或
【答案】D
【分析】本题考查了矩形的性质及全等三角形的判定与性质等知识点,数形结合、分类讨论并熟练掌握相关性质及定理是解题的关键.
当与全等时,有两种情况:①当时,,②当时,,分别按照全等三角形的性质及行程问题的基本数量关系求解即可.
【详解】解:当与全等时,有两种情况:
①当时,,
,,
,,
;
动点在线段上,从点出发以的速度向点运动,
点和点的运动时间为:,
∴;
②当时,,
,,
,,
,
,
综上,v的值为2或.
故选:D.
【变式7-2】(23-24八年级·湖南郴州·期中)如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为 .
【答案】或
【分析】本题主要考查正方形的性质,三角形全等的判定与性质,关键是要考虑到点P的两种情况,牢记三角形全等的性质是解本题的关键.根据由点P的运动情况可知,和全等分以下两种情况:①当点P在上运动时,②当点P在上运动时,利用三角形全等的性质建立关于等式求解,即可解题.
【详解】解:由点P的运动情况可知,和全等分以下两种情况:
①当点P在上运动时,
四边形为正方形,,
,,
,
要和全等,
即,
,
,解得;
②当点P在上运动时,
要和全等,
即,
,
,解得;
综上所述,t的值为或.
故答案为:或.
【变式7-3】(23-24八年级·河南郑州·期末)如图,在中,为高线,.点为上一点,,连接,交于点,若.
(1)猜想线段与的位置关系,并证明;
(2)若动点从点出发沿射线以每秒6个单位长度的速度运动,运动的时间为秒.
①当点在线段上时,是否存在的值,使得的面积为27?若存在,请求出的值;若不存在,请说明理由;
②动点从点出发沿线段以每秒2个单位长度的速度向终点运动,,两点同时出发,当点到达点时,,两点同时停止运动.设运动时间为秒,点是直线上一点,且,当与全等时,请直接写出的值.
【答案】(1),证明见解析
(2)①存在t的值,理由见解析,;②t的值为或
【分析】本题是三角形综合题,考查了全等三角形的判定和性质,直角三角形的性质,利用分类讨论思想解决问题是解题的关键.
(1)由全等三角形的性质可得,由余角的性质可得,即可求解;
(2)①由全等三角形的性质可得,由三角形的面积公式可求解;
②分两种情况讨论,由全等三角形的判定列出等式,即可求解.
【详解】(1)解:,理由如下:
在中,为高,
,
又,
,
,,
,
;
(2)解:①存在的值,使得的面积为27,理由如下:
,,
,
,
,,
由(1)可知,,
,
在线段上,
,
解得:;
②,
,
、当点在线段延长线上时,如图3,
,
,
,
当时,,
此时,,
解得:;
、当点在线段上时,如图4,
,
,
,
当时,,
此时,,
解得:;
综上所述,当与全等时,的值为或.
【题型8 全等三角形的应用】
【例8】(23-24八年级·贵州铜仁·期末)某同学根据数学知识原理制作了如图所示的一个测量工具----拐尺,其中O为AB的中点,CA⊥AB,BD⊥AB,CA=BD,现要测量一透明隔离房间的深度,如何使用此测量工具,说明理由.
【答案】理由见解析.
【分析】使AC与房间内壁在一条直线上,且C与一端点接触,然后人在BD的延长线上移动至F,使F、O、E三点正好在一条直线上,记下F点,这时量出DF长,即为房间深度CE.通过证△EAO≌△FBO,可得BF=AE,则BF-BD=AE-AC,即DF=CE.
【详解】解:如图,使AC与房间内壁在一条直线上,且C与一端点接触,然后人在BD的延长线上移动至F,使F,O,E三点正好在一条直线上,记下F点,这时量出DF长,即为房间深度CE.理由如下:由∠A=∠B=90°,OA=OB,∠EOA=∠FOB,
∴△EAO≌△FBO,
得BF=AE,
则BF-BD=AE-AC,即DF=CE.
【点睛】本题考核知识点:全等三角形判定的应用. 解题关键点:构造全等三角形.
【变式8-1】(23-24八年级·陕西西安·期中)如图,小刚站在河边的点A处,在河对面(小刚的正北方向)的点B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了20步到达一棵树C处,接着再向前走了20步到达D处,然后他左转直行,从点D处开始计步,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他恰好走了74步,并且小刚一步大约0.5米.由此小刚估计出了在点A处时他与电线塔的距离,请问他的做法是否合理?若合理,请求出在点A处时他与电线塔的距离;若不合理,请说明理由.
【答案】合理,37米
【分析】本题考查全等三角形的应用,根据可得出,由该全等三角形的性质,故可求解.
【详解】解:合理,理由如下:
根据题意,得.
在和中,
∴.
∴.
又∵小刚走完用了74步,一步大约0.5米,
∴(米).
∴小刚在点A处时他与电线塔的距离为37米.
【变式8-2】(23-24八年级·陕西西安·期末)小乐与朋友们周末去游乐园乘坐海盗船游玩,想了解海盗船摆动到最高点位置时的高度.如图,当静止时海盗船位于铅垂线上,转轴到地面的距离,在乘坐的过程中,当海盗船静止在点处时,,此时测得点到铅垂线的距离,当船头从处摆动到处时发现船头处在最高位置处,此时,.求点到地面的距离.
【答案】
【分析】本题主要考查了全等三角形的判定以及性质,过点作于点F,利用证明,由全等三角形的性质可得出,进而可求出的值,即点到地面的距离.
【详解】解:如图,过点作于点F,
∵,,
∴,
∴,
∴,
∴,
∴,
∴,
∴即点到地面的距离为.
【变式8-3】(23-24八年级·河南郑州·期末)茗阳阁位于河南省信阳市浉河区茶韵路一号,建成于2007年4月29日,是信阳新建的城市文化与形象的代表建筑之一.设两点分别为茗阳阁底座的两端(其中两点均在地面上).因为两点间的实际距离无法直接测量,某学习小组分别设计出了如下两种方案:甲:如图1,在平地上取一个可以直接到达点的点O,连接并延长到点C,连接并延长到点D,使,连接,测出的长即可.乙:如图2,先确定直线,过点B作,在点D处用测角仪确定,射线交直线于点C,最后测量的长即可得线段的长.
(1)请用所学知识论证甲、乙两种方案的合理性;
(2)如果让你参与测量,你会选择哪一种方案?请说明理由.
【答案】(1)见解析
(2)见解析
【分析】本题主要考查了全等三角形的应用.熟练掌握全等三角形的判定定理是解决问题的关键.
(1)甲方案作出的是全等三角形,然后根据全等三角形对应边相等测量的,所以是可行的;乙方案作出的也是全等三角形,然后根据全等三角形对应边相等测量的,所以也是可行的;
(2)选甲方案,使用工具操作容易;乙方案使用工具操作相对不容易,A,B间可视性未知.
【详解】(1)甲方案:
在与中,
,
∴,
∴,
乙方案
∵,
∴,
在与中,
,
∴,
∴.
(2)选甲种方案,理由:使用工具简单,只需要测量长度的刻度尺,容易操作;乙种方案使用工具需要测量长度的刻度尺和测量角度的测角仪,不容易操作,A,B间是否具备可视性.
21世纪教育网(www.21cnjy.com)
