人教版2024-2025学年八年级数学上册举一反三专题13.7与轴对称图形有关的最值问题【八大题型】(学生版+解析)
文档属性
| 名称 | 人教版2024-2025学年八年级数学上册举一反三专题13.7与轴对称图形有关的最值问题【八大题型】(学生版+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 14:31:28 | ||
图片预览




文档简介
专题13.7 与轴对称图形有关的最值问题【八大题型】
【人教版】
【题型1 垂线段最短】 1
【题型2 两点之间线段最短】 2
【题型3 平行线之间的距离】 4
【题型4 两动一定】 6
【题型5 两定一动(将军饮马)】 7
【题型6 两定两动型】 9
【题型7 两定一动(三点共线)】 10
【题型8 两动+定长】 11
知识点1:垂线段最短
【模型分析】
如图,点P在直线l外,过点P作l的垂线PH,则点P到直线l的距离为PH,即“垂线段最短”.
【温馨提示】解决最值问题常遵循:一找、二证、三计算.
【方法解读】
若所求线段不能直接利用“垂线段最短求最值”,需将其转化到定点和动点之间的线段,可借助矩形的对角线相等或全等三角形的性质.
【题型1 垂线段最短】
【例1】(23-24八年级·江苏盐城·期末)如图, 线段,是线段外一点,连接、,、分别是、的中点,连接、交于点.当四边形的面积为10时,线段的最小值为 .
【变式1-1】(23-24八年级·湖南娄底·阶段练习)如图,平分,于点E,F是射线上的任一点,,则的长度不可能是( )
A.4.2 B.5.15 C.3.69 D.8
【变式1-2】(23-24八年级·吉林·期中)如图,是一条河流,要铺设管道将河水引到两个用水点和,现有两种铺设管道的方案,若铺设管道单位长度的造价均相同,则下列说法正确的是( )
方案一:分别过,作的垂线,垂足为,,沿,铺设管道;
方案二:连接交于点,沿,铺设管道.
A.方案一与方案二一样省钱,因为管道长度一样
B.方案二比方案一省钱,因为两点之间,线段最短
C.方案一比方案二省钱,因为垂线段最短
D.方案一与方案二无法比较
【变式1-3】(23-24八年级·江西南昌·期末)如图,钝角的面积为12,最长边,平分,点M、N分别是上的动点,则的最小值是 .
【题型2 两点之间线段最短】
【例2】(23-24八年级·湖南郴州·期末)利用轴对称的性质解决路程之和最短的问题,如图所示,河岸的同侧有、两个村庄,两村委会决定在小河边建一座自来水加工厂向两村庄输送自来水,为了节约开支,加工厂建在何处所需铺设的管道最短?为什么?
【变式2-1】(23-24八年级·广东佛山·期末)如图所示,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资建一个蓄水池,不考虑其他因素,请画图确定蓄水池H点位置,使它与四个村庄的距离之和最小.
【变式2-2】(23-24八年级·陕西西安·期中)(1)如图1,在平面直角坐标系中,点的坐标分别为,现同时将点分别向上平移2个单位,再向右平移1个单位,分别得到点的对应点,连接,,直接写出点的坐标______,的坐标______及四边形的面积为______.
(2)如图2,A,B两单位分别位于一条封闭街道的两旁(直线是街道两边沿),现准备修建一座过街人行天桥.天桥应建在何处才能使由A经过天桥走到的路程最短?在图3中作出此时天桥的位置,简要叙述作法并保留作图痕迹(注:桥的宽度忽略不计,桥必须与街道垂直).
【变式2-3】(23-24六年级下·山东烟台·期中)如图,在同一平面内,点D、E是三角形外的两点,请按要求完成下列问题.
(1)请你判断线段与的大小关系是 ;理由是 ;
(2)①按要求将图形补充完整:连接线段,画射线、直线;
②若在四边形的边、、、上任取一点,分别为点K、L、M、N,并顺次连接它们,则四边形的周长 四边形的周长.(大于、小于或等于)
(3)在四边形内找一点O,使它到四边形四个顶点的距离之和最小.(保留作图痕迹,找到点即可)
【题型3 平行线之间的距离】
【例3】(23-24八年级·安徽合肥·期末)如图,,且相邻两条直线间的距离都是2,A,B,C分别为,,上的动点,连接AB、AC、BC,AC与交于点D,,则BD的最小值为( )
A.2 B.3 C.4 D.5
【变式3-1】(23-24八年级·北京海淀·期中)如图,在△ABC中,∠C=90°,BD为△ABC的角平分线,过点D作直线lAB,点P为直线l上的一个动点,若△BCD的面积为16,BC=8,则AP最小值为 .
【变式3-2】(23-24八年级·广东深圳·期末)如图,在四边形中,,,,面积为18,的垂直平分线分别交,于点,,若点和点分别是线段和边上的动点,则的最小值为 .
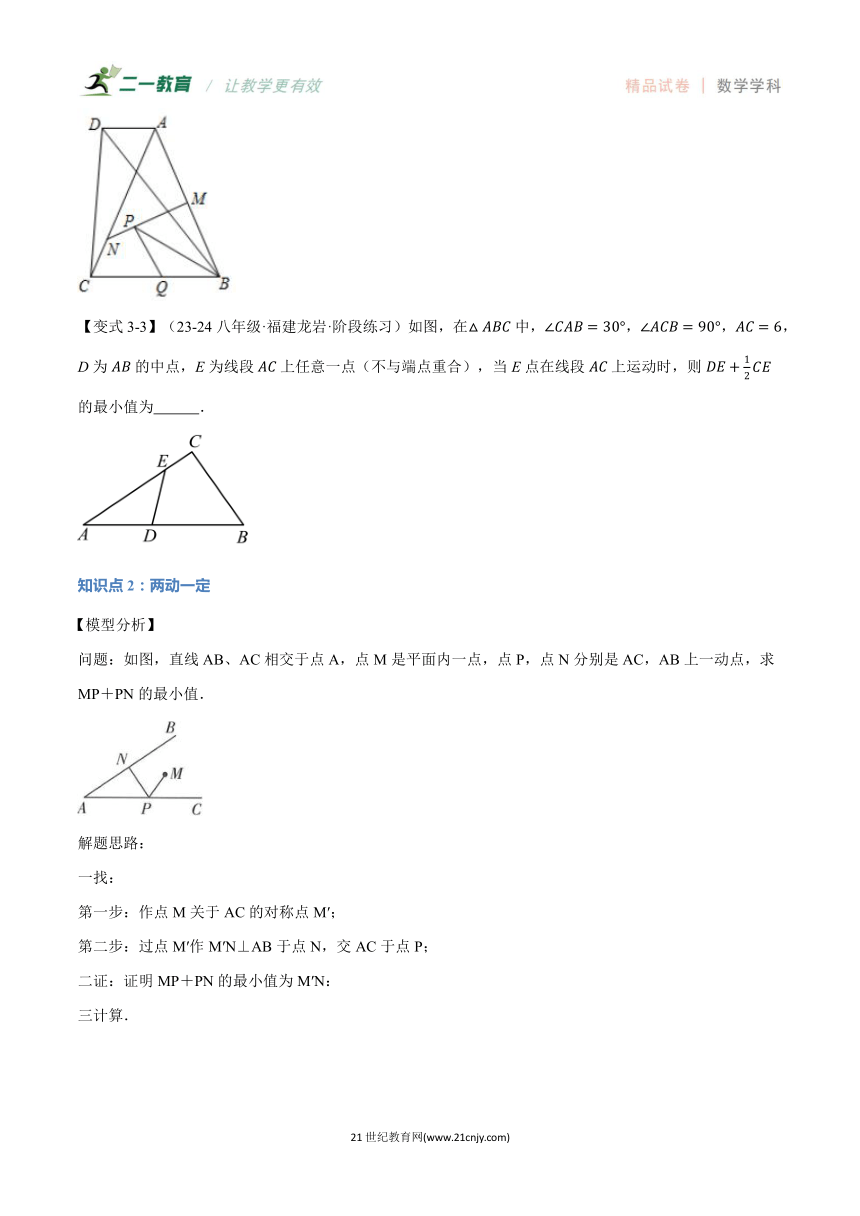
【变式3-3】(23-24八年级·福建龙岩·阶段练习)如图,在中,,,,D为的中点,E为线段上任意一点(不与端点重合),当E点在线段上运动时,则的最小值为 .
知识点2:两动一定
【模型分析】
问题:如图,直线AB、AC相交于点A,点M是平面内一点,点P,点N分别是AC,AB上一动点,求MP+PN的最小值.
解题思路:
一找:
第一步:作点M关于AC的对称点M′;
第二步:过点M′作M′N⊥AB于点N,交AC于点P;
二证:证明MP+PN的最小值为M′N:
三计算.
【题型4 两动一定】
【例4】(23-24八年级·广东珠海·期末)已知,在内有一定点P,点M,N分别是,上的动点,若的周长最小值为3,则的长为( )
A. B.3 C. D.
【变式4-1】(23-24八年级·安徽淮北·期末)如图,在中,,的面积为18,,平分,,分别是,上的动点,则的最小值为( )
A.4 B.6 C.7 D.9
【变式4-2】(23-24八年级·全国·专题练习)如图所示,在等边中,点D、E、F分别在边、,上,则线段的最小值是( )
A.边上高的长 B.线段的长度
C.边的长度 D.以上都不对
【变式4-3】(23-24八年级·湖南株洲·期中)如图,在等腰中,在、上分别截取、,使.再分别以点,为圆心,以大于的长为半径作弧,两弧在内交于点,作射线,交于点.已知,,.若点、分别是线段和线段上的动点,则的最小值为( )
A. B. C. D.
知识点3:两定一动
已知:在l上求作一点M,使得AM+BM最小.
【题型5 两定一动(将军饮马)】
【例5】(23-24八年级·宁夏银川·期末)如图,在中,,,,垂直平分,点P为直线上任意一点,则的最小值是 .
【变式5-1】(23-24八年级·广东揭阳·期末)如图,在长度为1个单位长度的小正方形组成的正方形网格中,点、、在小正方形的顶点上.
(1)在图中画出与关于直线成轴对称的.
(2)在直线上找一点,使的长最短.
【变式5-2】(23-24八年级·江西宜春·期末)如图,在中,边的垂直平分线交于点D,若,
(1)求的长;
(2)若点P是直线上的动点,直接写出的最小值为_________.
【变式5-3】(23-24八年级·河南周口·阶段练习)已知点P在内.
(1)如图①,点P关于射线的对称点分别是G、H,连接.
①若,则是什么特殊三角形?为什么?
②若,试判断与的数量关系,并说明理由;
(2)如图②,若, A、B分别是射线上的点,于点B,点P、Q分别为上的两个定点,且,,在上有一动点E,试求的最小值.
知识点4:两定两动
已知:在平面直角坐标系中,点P (2,3),Q (3,2),请在x轴和y轴上分别找到M点和N点,使四边形PQMN周长最小.作出M点和N点.
【题型6 两定两动型】
【例6】(23-24·福建莆田·中考模拟)如图,,,,、分别为、上的两个动点,则的最小值为______.
【变式6-1】(23-24八年级·江苏南京·期末)如图,在四边形ABCD中,∠BAD=∠B=∠D=90°,AD=AB=4,E是AD中点,M是边BC上的一个动点,N是边CD上的一个动点,则AM+MN+EN的最小值是 .
【变式6-2】(23-24八年级·河南安阳·阶段练习)如图,在矩形中,对角线上有两动点和,连接和,若,,则的最小值是( )
A.4 B.10 C.6 D.20
【变式6-3】(23-24八年级·广东江门·阶段练习)在中,分别为射线与射线上的两动点,且,连接,则最小值为 .
【题型7 两定一动(三点共线)】
【例7】(23-24八年级·浙江宁波·开学考试)如图,在中,,.延长线段至点,使,过点作射线,点为射线上的动点,分别过点,作直线的垂线,.当的值最大时,的度数为 .
【变式7-1】(23-24八年级·福建福州·期中)如图,在等边中,E是边的中点,P是的中线上的动点,且,则的最大值是 .
【变式7-2】(23-24八年级·湖北武汉·期末)如图,,在直线上方作等腰,,,连接,当最大时, .
【变式7-3】(23-24八年级·河北张家口·期末)如图,方格图中每个小正方形的边长为1,点A、B、C、M、N都在格点上.
(1)画出关于直线对称的;
(2)在直线上找点P使最小,在图形上画出点P的位置;
(3)在直线上找点Q使最大,直接写出这个最大值.
【题型8 两动+定长】
【例8】(23-24八年级·浙江绍兴·期末)如图,在平面直角坐标系中,,,,M,N是线段上的两个动点,且,则与周长和的最小值是 .
【变式8-1】(23-24八年级·全国·专题练习)如图,长方形中,,线段在边上左右滑动,若,则的最小值为 .
【变式8-2】(23-24八年级·湖北恩施·阶段练习)已知,如图,线段长为,于,于,,,为线段上两动点,在右侧且,则由到的路径:的最小值为 .
【变式8-3】(23-24八年级·江苏南通·阶段练习)如图,在平面直角坐标系中,点A(1,0),点B(2,0),点C,D是y轴上两个动点(点D在点C下方)且CD=2,连接AC,BD,则AC+BD的最小值为
21世纪教育网(www.21cnjy.com)
专题13.7 与轴对称图形有关的最值问题【八大题型】
【人教版】
【题型1 垂线段最短】 2
【题型2 两点之间线段最短】 5
【题型3 平行线之间的距离】 9
【题型4 两动一定】 13
【题型5 两定一动(将军饮马)】 17
【题型6 两定两动型】 23
【题型7 两定一动(三点共线)】 29
【题型8 两动+定长】 34
知识点1:垂线段最短
【模型分析】
如图,点P在直线l外,过点P作l的垂线PH,则点P到直线l的距离为PH,即“垂线段最短”.
【温馨提示】解决最值问题常遵循:一找、二证、三计算.
【方法解读】
若所求线段不能直接利用“垂线段最短求最值”,需将其转化到定点和动点之间的线段,可借助矩形的对角线相等或全等三角形的性质.
【题型1 垂线段最短】
【例1】(23-24八年级·江苏盐城·期末)如图, 线段,是线段外一点,连接、,、分别是、的中点,连接、交于点.当四边形的面积为10时,线段的最小值为 .
【答案】6
【分析】本题考查了三角形中线等分面积,垂线段最短,关键是由三角形面积公式求出的面积.
【详解】解:过作于,连接,延长交于,
、分别是、的中点,
的面积面积的一半,的面积面积的一半,
的面积的面积,
的面积四边形的面积,
、分别是、的中点,
的面积的面积,的面积的面积.
的面积的面积的面积的面积四边形的面积,
的面积,
的面积,
,
,
,
线段的最小值是6.
故答案为:6.
【变式1-1】(23-24八年级·湖南娄底·阶段练习)如图,平分,于点E,F是射线上的任一点,,则的长度不可能是( )
A.4.2 B.5.15 C.3.69 D.8
【答案】C
【分析】本题考查了角平分线的性质,垂线段最短等,过D点作于点H,根据角平分线的性质得到,再根据垂线段最短进行判断即可.
【详解】解:过D点作于点H,如图所示:
平分,
,
是射线上的任一点,
,
,
∴的长不能为3.69.
故选:C.
【变式1-2】(23-24八年级·吉林·期中)如图,是一条河流,要铺设管道将河水引到两个用水点和,现有两种铺设管道的方案,若铺设管道单位长度的造价均相同,则下列说法正确的是( )
方案一:分别过,作的垂线,垂足为,,沿,铺设管道;
方案二:连接交于点,沿,铺设管道.
A.方案一与方案二一样省钱,因为管道长度一样
B.方案二比方案一省钱,因为两点之间,线段最短
C.方案一比方案二省钱,因为垂线段最短
D.方案一与方案二无法比较
【答案】C
【分析】本题考查垂线段的性质,即垂线段最短.根据垂线段最短可得,,进而得出结论.解题的关键是掌握:垂线段最短指的是从直线外一点到这条直线所作的垂线段最短.实际问题中涉及线路最短问题时,其理论依据应从“两点之间,线段最短”和“垂线段最短”这两个中去选择.
【详解】解:∵,,
∴,,
∴,
∴按照方案一铺设管道的长度比按照方案二铺设管道的长度更短,
∵铺设管道单位长度的造价均相同,
∴方案一比方案二省钱.
故选:C.
【变式1-3】(23-24八年级·江西南昌·期末)如图,钝角的面积为12,最长边,平分,点M、N分别是上的动点,则的最小值是 .
【答案】3
【分析】本题考查了轴对称—最短路线问题,关键是画出符合条件的图形,题目具有一定的代表性,是一道比较好的题目.过点C作于点E,交于点M,过点M作于N,则当点C,M,N三点重合时,取得最小值,最小值为的长.再根据三角形的面积公式求出的长,即可.
【详解】解:过点C作于点E,交于点M,过点M作于N,
∵平分,,,
∴,
∴,
即当点C,M,N三点重合时,取得最小值,最小值为的长.
∵的面积为12,最长边,
∴,即,
∴
即的最小值为3.
故答案为:3.
【题型2 两点之间线段最短】
【例2】(23-24八年级·湖南郴州·期末)利用轴对称的性质解决路程之和最短的问题,如图所示,河岸的同侧有、两个村庄,两村委会决定在小河边建一座自来水加工厂向两村庄输送自来水,为了节约开支,加工厂建在何处所需铺设的管道最短?为什么?
【答案】见解析
【分析】此题主要考查了轴对称作图与应用设计,作点关于直线的对称点,连接,交直线于点,点即为所求;关键是正确找出点的位置.
【详解】解:如图,作点关于直线的对称点,连接,交直线于点,
由作图可知:,
要使的从点到点的路程最短,根据两点之间线段最短,连接,交直线于点,点即为所求;
故加工厂应该建在处.
【变式2-1】(23-24八年级·广东佛山·期末)如图所示,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资建一个蓄水池,不考虑其他因素,请画图确定蓄水池H点位置,使它与四个村庄的距离之和最小.
【答案】答案见解析
【分析】本题属于最短路线问题,解决此类题目的关键是掌握最有关短路径的知识点.
依据“两点之间线段最短”直接连接线段和,其交点H即为所求的点.
【详解】解:如下图所示,连接线段和,应把蓄水池建在交点上,因为这样H点既在线段上,又在线段上,由“两点之间,线段最短"可知,此时蓄水池与四个村庄的距离之和最小.
【变式2-2】(23-24八年级·陕西西安·期中)(1)如图1,在平面直角坐标系中,点的坐标分别为,现同时将点分别向上平移2个单位,再向右平移1个单位,分别得到点的对应点,连接,,直接写出点的坐标______,的坐标______及四边形的面积为______.
(2)如图2,A,B两单位分别位于一条封闭街道的两旁(直线是街道两边沿),现准备修建一座过街人行天桥.天桥应建在何处才能使由A经过天桥走到的路程最短?在图3中作出此时天桥的位置,简要叙述作法并保留作图痕迹(注:桥的宽度忽略不计,桥必须与街道垂直).
【答案】(1);8(2)见解析
【分析】本题考查坐标与图形性质;点的平移和三角形的面积,解答的关键得到四边形ACDB是平行四边形,
(1)根据点的平移规律即可得点C,D的坐标;由 即可计算出;
(2)沿竖直方向向下平移点A,使得平移的距离等于桥长,再根据两点之间线段最短,确定桥的位置即可;
【详解】解:(1)依题意,得,
∴;
(2)如图,将点A沿竖直向下的方向平移,平移距离等于桥长,到达点,连接,与街道交于点,过点建桥即符合要求;
【变式2-3】(23-24六年级下·山东烟台·期中)如图,在同一平面内,点D、E是三角形外的两点,请按要求完成下列问题.
(1)请你判断线段与的大小关系是 ;理由是 ;
(2)①按要求将图形补充完整:连接线段,画射线、直线;
②若在四边形的边、、、上任取一点,分别为点K、L、M、N,并顺次连接它们,则四边形的周长 四边形的周长.(大于、小于或等于)
(3)在四边形内找一点O,使它到四边形四个顶点的距离之和最小.(保留作图痕迹,找到点即可)
【答案】(1);两点之间线段最短
(2)①见解析;②小于
(3)见解析
【分析】本题考查直线、射线、线段等的作图以及两点之间、线段最短:
(1)根据两点之间线段最短判断即可;
(2)根据直线,射线,线段的定义以及题目要求作出图形即可;
(3)连接、,交于点,根据两点之间线段最短即可判断点即为所求.
解题的关键是理解直线,射线,线段的定义,灵活应用所学知识解决问题.
【详解】(1)解:根据两点之间线段最短得:,
故答案为:;两点之间线段最短.
(2)①如图所示,线段,射线、直线即为所求;
②如图:
,,,,
,即:四边形的周长小于四边形的周长,
故答案为:小于.
(3)连接、,交于点,
根据两点之间线段最短可知,,
即:此时点四边形四个顶点的距离之和最小,
如图所示,点即为所求.
【题型3 平行线之间的距离】
【例3】(23-24八年级·安徽合肥·期末)如图,,且相邻两条直线间的距离都是2,A,B,C分别为,,上的动点,连接AB、AC、BC,AC与交于点D,,则BD的最小值为( )
A.2 B.3 C.4 D.5
【答案】A
【分析】求BD的最小值可以转化为求点B到直线AC的距离,当BD⊥AC时,BD有最小值,根据题意求解即可.
【详解】解:由题意可知当BD⊥AC时,BD有最小值,
此时,AD=CD,∠ABC=90°,
∴BD=AD=BD=AC=2,
∴BD的最小值为2.
故选:A.
【点睛】本题考查平行线的性质,需结合图形,根据平行线的性质推出相关角的关系从而进行求解.
【变式3-1】(23-24八年级·北京海淀·期中)如图,在△ABC中,∠C=90°,BD为△ABC的角平分线,过点D作直线lAB,点P为直线l上的一个动点,若△BCD的面积为16,BC=8,则AP最小值为 .
【答案】4
【分析】根据三角形的面积公式求得CD,再根据角平分的性质求得DE,根据平行线之间的距离可得AP的最小值.
【详解】解:∵∠C=90°,△BCD的面积为16,BC=8,
∴,即,
作DE⊥AB,
∵BD为△ABC的角平分线,
∴,
∵直线lAB,
∴AP最小值与DE相等为4,
故答案为:4.
【点睛】本题考查角平分线的性质,平行线之间的距离,理解平行线之间距离的定义和点到直线的距离垂线段最短是解题关键.
【变式3-2】(23-24八年级·广东深圳·期末)如图,在四边形中,,,,面积为18,的垂直平分线分别交,于点,,若点和点分别是线段和边上的动点,则的最小值为 .
【答案】6
【分析】连接AQ,过点D作于H.利用三角形的面积公式求出DH,由题意得: ,求出AQ的最小值,AQ最小值是与DH相等,也就是时,根据面积公式求出DH的长度即可得到结论.
【详解】解:连接AQ,过点D作于H.
∵面积为18,BC=6,
∴,
∴,
∵MN垂直平分线段AB,
∴,
∴,
∴当AQ的值最小时,的值最小,
根据垂线段最短可知,当时,AQ的值最小,
∵,
∴AQ=DH=6,
∴的最小值为6.
故答案为:6.
【点睛】本题考查轴对称最短问题,平行线的性质,三角形的面积,线段的垂直平分线的性质等知识,把最短问题转化为垂线段最短是解题关键.
【变式3-3】(23-24八年级·福建龙岩·阶段练习)如图,在中,,,,D为的中点,E为线段上任意一点(不与端点重合),当E点在线段上运动时,则的最小值为 .
【答案】3
【分析】过C作,过C作,过D作的垂线交于点F交于点E,即可得到答案;
【详解】解:过C作,过D作的垂线交于点F,
∵,,,
∴,
∴即为最小值,
∵,,,
∴,,
∵,,
∴,
故答案为:3;
【点睛】本题考查角所对直角边等于斜边一半及平行线间距离处处相等且最短.
知识点2:两动一定
【模型分析】
问题:如图,直线AB、AC相交于点A,点M是平面内一点,点P,点N分别是AC,AB上一动点,求MP+PN的最小值.
解题思路:
一找:
第一步:作点M关于AC的对称点M′;
第二步:过点M′作M′N⊥AB于点N,交AC于点P;
二证:证明MP+PN的最小值为M′N:
三计算.
【题型4 两动一定】
【例4】(23-24八年级·广东珠海·期末)已知,在内有一定点P,点M,N分别是,上的动点,若的周长最小值为3,则的长为( )
A. B.3 C. D.
【答案】B
【分析】根据题意画出符合条件的图形,求出,得出等边三角形,求出,求出的周长,即可求出答案.
【详解】解:作P关于的对称点D,作P关于的对称点E,连接交于M,交于N,连接,则此时的周长最小,
连接,
∵P、D关于对称,
∴,
同理,
∴,
∵P、D关于对称,
∴,
∵,
∴,
同理,
∴,
∵,
∴是等边三角形,
∴,
∵的周长是,
∴
故选:B.
【点睛】本题考查了轴对称-最短路线问题,等边三角形的判定与性质,关键是画出符合条件的图形.
【变式4-1】(23-24八年级·安徽淮北·期末)如图,在中,,的面积为18,,平分,,分别是,上的动点,则的最小值为( )
A.4 B.6 C.7 D.9
【答案】A
【分析】过点C作于点P,交于点E,过点E作于F,则即为的最小值,再根据三角形的面积公式求出的长,即为的最小值.
【详解】解:过点C作于点P,交于点E,过点E作于F,
∵平分,,,
∴,
∴的最小值.
∵的面积为18,,
∴,
∴.
即的最小值为4,
故选:A.
【点睛】本题考查了轴对称-最短路线问题,关键是将的最小值为转化为,题目具有一定的代表性,是一道比较好的题目.
【变式4-2】(23-24八年级·全国·专题练习)如图所示,在等边中,点D、E、F分别在边、,上,则线段的最小值是( )
A.边上高的长 B.线段的长度
C.边的长度 D.以上都不对
【答案】A
【分析】作于点D,当、时,线段有最小值,根据等边三角形的性质可得,进而得结论.
【详解】解:如图,作于点D,当、时,线段有最小值,
∵是等边三角形,
∴,
∵,
∴,
∴,
∴,
∴线段的最小值是边上高的长.
故选:A.
【点睛】本题考查了轴对称-最短路线问题、等边三角形的性质,解决本题的关键是掌握等边三角形的性质.
【变式4-3】(23-24八年级·湖南株洲·期中)如图,在等腰中,在、上分别截取、,使.再分别以点,为圆心,以大于的长为半径作弧,两弧在内交于点,作射线,交于点.已知,,.若点、分别是线段和线段上的动点,则的最小值为( )
A. B. C. D.
【答案】C
【分析】本题考查了等腰三角形的性质,垂线段最短;过点B作于点H,交于点,根据等面积法,可得.作点H关于的对称点交于点N,连接,可得,进而可以解决问题.
【详解】解:如图,过点B作于点H,交于点,
由作图可知,平分,
∵,
∴,
∵,
∴,
∴.
∵,,
作点H关于的对称点交于点N,连接,
∴,
∴,
则的最小值为.
故选C.
知识点3:两定一动
已知:在l上求作一点M,使得AM+BM最小.
【题型5 两定一动(将军饮马)】
【例5】(23-24八年级·宁夏银川·期末)如图,在中,,,,垂直平分,点P为直线上任意一点,则的最小值是 .
【答案】4
【分析】由线段垂直平分线的性质可得,可得当点A,P,C在一条直线上时,有最小值,最小值为的长.
【详解】解:连接.
∵是的垂直平分线,
∴,
∴,
∴当点A,P,C在一条直线上时,有最小值,最小值为.
故答案为:4.
【点睛】本题考查了线段垂直平分线的性质,明确线段垂直平分线上的点到线段两端点的距离相等是解题的关键.
【变式5-1】(23-24八年级·广东揭阳·期末)如图,在长度为1个单位长度的小正方形组成的正方形网格中,点、、在小正方形的顶点上.
(1)在图中画出与关于直线成轴对称的.
(2)在直线上找一点,使的长最短.
【答案】(1)见解析
(2)见解析
【详解】(1)解:如图,△即为所求.
(2)如图,点即为所求.
【点睛】本题考查作图轴对称变换、轴对称最短路线问题,熟练掌握轴对称的性质是解答本题的关键.
【变式5-2】(23-24八年级·江西宜春·期末)如图,在中,边的垂直平分线交于点D,若,
(1)求的长;
(2)若点P是直线上的动点,直接写出的最小值为_________.
【答案】(1)9
(2)9
【分析】(1)根据垂直平分线的性质可证为等腰三角形,由角度可证为直角三角形,再由线段之间的关系即可求出的长;
(2)根据将军饮马原理即可得出的最小值为的长度.
【详解】(1)解:∵,
∴
∵边的垂直平分线交于点D,
∴,
∴
∴
在中,
∴
∴
(2)解:如图,
取点关于直线的对称点,即点;连接两点,与直线交于点,
根据两点之间线段最短
则即为的最小值,最小值为9
【点睛】本题考查了图形的轴对称,相关知识点有:垂直平分线的性质、将军饮马等,轴对称性质的充分利用是解题关键.
【变式5-3】(23-24八年级·河南周口·阶段练习)已知点P在内.
(1)如图①,点P关于射线的对称点分别是G、H,连接.
①若,则是什么特殊三角形?为什么?
②若,试判断与的数量关系,并说明理由;
(2)如图②,若, A、B分别是射线上的点,于点B,点P、Q分别为上的两个定点,且,,在上有一动点E,试求的最小值.
【答案】(1)①是等边三角形,理由见解析;②,理由见解析
(2)的最小值为5.
【分析】(1)①由轴对称的性质可得,,.根据“有一个角是的等腰三角形是等边三角形”即可得出是等边三角形;②当时,,G、O、H在同一直线上,由此可得与的数量关系;
(2)过Q作的对称点,连接,交于点E,连接,则的最小值为,由已知条件可得,易得,,由此可得是等边三角形,即可得的长,即的最小值.
【详解】(1)解:①是等边三角形,
∵点P关于对称的点为G,
∴,,
同理,,
∴,
∵,
∴,
∴是等边三角形.
②,
当时,,
∴G、O、H在同一直线上,.
∵,
∴;
(2)解:过Q作的对称点,连接,交于点E,连接,
∴ 最小值为.
∵,,
∴.
∵,,
∴,
∴,
∴.
∵点Q与关于对称,
∴,
∴,
∴是等边三角形,
∴,
即的最小值为5.
【点睛】本题主要考查了轴对称--最短路线问题,轴对称的性质和等边三角形的判定和性质.熟练掌握轴对称的性质及等边三角形的判定和性质,熟悉“将军饮马”模型是解题的关键.
知识点4:两定两动
已知:在平面直角坐标系中,点P (2,3),Q (3,2),请在x轴和y轴上分别找到M点和N点,使四边形PQMN周长最小.作出M点和N点.
【题型6 两定两动型】
【例6】(23-24·福建莆田·中考模拟)如图,,,,、分别为、上的两个动点,则的最小值为______.
【答案】
【解析】解:如图,连接,,
,,,
≌,
,
同理可得:,
,
当点,点,点,点共线时,有最小值,即最小值为的长度,
有最小值为,
故答案为:.
由“”可证≌,可得,,由,可得当点,点,点,点共线时,有最小值,即可求解.
本题考查了轴对称最短路线问题,全等三角形的判定和性质,证明,是本题的关键.
【变式6-1】(23-24八年级·江苏南京·期末)如图,在四边形ABCD中,∠BAD=∠B=∠D=90°,AD=AB=4,E是AD中点,M是边BC上的一个动点,N是边CD上的一个动点,则AM+MN+EN的最小值是 .
【答案】10
【分析】作A点关于BC的对称点A1,连接A1M,作E点关于DC的对称点E1,连接E1N,因此,所以最小值为,用勾股定理算出即可.
【详解】解:如图,作A点关于BC的对称点A1,连接A1M,作E点关于DC的对称点E1,连接E1N,
∵∠B=∠D=90°,点A和点A1关于BC对称,点E和点E1关于DC对称,
∴,,
∴,
∴AM+MN+EN的最小值是,
∵AD=AB=4,E是AD中点,
∴,,
∴,,
∵∠BAD=90°,
∴,
故答案为:10.
【点睛】本题考查了线段和的最值问题,勾股定理、轴对称性质,作出辅助线是本题的关键.
【变式6-2】(23-24八年级·河南安阳·阶段练习)如图,在矩形中,对角线上有两动点和,连接和,若,,则的最小值是( )
A.4 B.10 C.6 D.20
【答案】B
【分析】如图,连接,,由全等三角形判定可以证得,得到,进而得到,再根据题意及勾股定理求出的值,即可得出答案.
【详解】解:如图,连接,,
四边形是矩形,
,,,
,
,
,
,
,
,
又 ,为矩形的对角线,
,
是直角三角形,,
,
解得,或
,则不符合题意,
,
,
故选B.
【点睛】本题考查了矩形的性质,全等三角形的判定与性质,两点之间线段最短,勾股定理的应用及解一元二次方程,熟知相关的判定与性质及解一元二次方程的方法是解题关键.
【变式6-3】(23-24八年级·广东江门·阶段练习)在中,分别为射线与射线上的两动点,且,连接,则最小值为 .
【答案】
【分析】本题考查了全等三角形的性质与判定以及勾股定理;过点作,使得,过点作于点,连接,证明得出 ,则当在线段上时,取的最小值,最小值为的长,
【详解】解:如图,过点作,使得,过点作于点,连接,
在中,
,
∴,
∴,
∴,
则当在线段上时,取的最小值,最小值为的长,
∵,,,
∴
∵,
∴,
在中,,
∴,
∴,
故答案为:.
【题型7 两定一动(三点共线)】
【例7】(23-24八年级·浙江宁波·开学考试)如图,在中,,.延长线段至点,使,过点作射线,点为射线上的动点,分别过点,作直线的垂线,.当的值最大时,的度数为 .
【答案】/130度
【分析】本题考查了全等三角形的判定和性质,平行线的性质,等腰三角形的判定和性质.如图,过点作直线于点.证明,推出与重合时,的值最大,此时,画出相应的图形,根据条件,利用三角形的内角和、邻补角的意义,求出结果.
【详解】解:如图,过点作直线于点.
直线,直线,
,
,,
,
,
,
与重合时,的值最大,
当与重合,与重合时,的值最大,此时,
,
,
,
,
,
又,
,
,
故答案为:.
【变式7-1】(23-24八年级·福建福州·期中)如图,在等边中,E是边的中点,P是的中线上的动点,且,则的最大值是 .
【答案】3
【分析】连接PC,则BP=CP,=CP-PE,当点P与点A重合时,CP-PE=CE,进而即可求解.
【详解】解:连接PC,
∵在等边中,,P是的中线上的动点,
∴AD是BC的中垂线,
∴BP=CP,
∴=CP-PE,
∵在中,CP-PE<CE,
∴当点P与点A重合时,CP-PE=CE,
∵E是边的中点,
∴的最大值=6÷2=3.
故答案是:3.
【点睛】本题主要考查等边三角形的性质,三角形三边长关系,连接CP,得到=CP-PE,是解题的关键.
【变式7-2】(23-24八年级·湖北武汉·期末)如图,,在直线上方作等腰,,,连接,当最大时, .
【答案】
【分析】构造等腰,如图1,使,,则,,当、、三点共线时,最大,然后根据已知角及等腰三角形的性质即可求解.
【详解】解:如图1,构造等腰,使,,
则,,
∴当、、共线时,最大,
此时,如图2所示,
,,则,
∴,
∵,,
∴,
∴.
故答案为:45°.
【点睛】本题主要考查了等腰三角形的性质、三角形全等的判定和性质,解题的关键是准确作出辅助线,找出当最大时的图形.
【变式7-3】(23-24八年级·河北张家口·期末)如图,方格图中每个小正方形的边长为1,点A、B、C、M、N都在格点上.
(1)画出关于直线对称的;
(2)在直线上找点P使最小,在图形上画出点P的位置;
(3)在直线上找点Q使最大,直接写出这个最大值.
【答案】(1)见解析
(2)见解析
(3)作图见解析;最大值为3
【分析】(1)利用网格特点,先画出A、B、C关于直线的对称点、、,再顺次连接即可;
(2)作点C关于的对称点D,连接交于一点,该点即为点P;
(3)由于,则,而由三角形的三边关系可得,当Q、、B三点共线时取等号,从而可得答案.
【详解】(1)解:即为所求作的三角形,如图所示:
(2)解:如图,作点C关于的对称点D,连接交于一点,该点即为所求作的点P;
∵点C与D关于的对称,
∴,
∴,
∵,只有当点P、B、D三点共线时等号成立,
∴当点P、B、D三点共线时,最小,即最小;
(3)解:先作出A关于直线的对称点,连接并延长交于一点,该点即为点Q,如图所示:
∵,
∴,
根据三角形的三边关系可得,当Q、、B三点共线时取等号,
∴的最大值为.
【点睛】本题主要考查了作图—轴对称变换、轴对称的性质和三角形的三边关系,属于常考题型,熟练掌握上述知识是解题的关键.
【题型8 两动+定长】
【例8】(23-24八年级·浙江绍兴·期末)如图,在平面直角坐标系中,,,,M,N是线段上的两个动点,且,则与周长和的最小值是 .
【答案】
【分析】将点C项左平移2个单位得到,找出点A关于x轴的对称点,连接交x轴于一点即为最短距离点,根据勾股定理即可得到答案;
【详解】解:由题意可得,
,
∵,,,
∴当最小即可得到答案,
点C项左平移2个单位得到,找出点A关于x轴的对称点,连接交x轴于一点即为最短距离点,如图所示,
根据勾股定理可得,
,
∴与周长和的最小值是:,
故答案为:.
【点睛】本题考查最短距离问题及勾股定理,解题的关键是根据轴对称的性质及两点间线段距离最短得到最小距离位置.
【变式8-1】(23-24八年级·全国·专题练习)如图,长方形中,,线段在边上左右滑动,若,则的最小值为 .
【答案】
【分析】取,作关于的对称点,连接,得出四边形是平行四边形,继而可得 ,当三点共线时,最小,最小值为,勾股定理即可求解.
【详解】解:如图,取,作关于的对称点,连接,
∴,
∵,
∴四边形是平行四边形,
∴,
∴ ,
∴当三点共线时,最小,最小值为,
此时,
在中,,
即的最小值为,
故答案为:.
【点睛】本题考查了勾股定理,轴对称求线段和的最值问题,掌握轴对称的性质是解题的关键.
【变式8-2】(23-24八年级·湖北恩施·阶段练习)已知,如图,线段长为,于,于,,,为线段上两动点,在右侧且,则由到的路径:的最小值为 .
【答案】/
【分析】过点作且,作关于的对称点,连接交于点,连接交于点,过点作交于,证明,再根据全等三角形的性质,得出,再根据轴对称的性质,得出,进而得出,再根据两点之间线段最短,得出的最小值为的长,此时,的值最小,过点作交的延长线于,再根据线段之间的数量关系,得出,,再根据勾股定理,得出,进而即可得出答案.
【详解】解:过点作且,作关于的对称点,连接交于点,连接交于点,过点作交于,
∵,
∴,
∵,,
∴,
∴,
∵关于的对称点,
∴,
∴,
∴,
∴的最小值为的长,此时,的值最小,
过点作交的延长线于,
∴,
∵,
∴,
∴,
∴的最小值为.
故答案为:
【点睛】本题考查了全等三角形的判定与性质、轴对称的性质、两点之间线段最短、勾股定理,解本题的关键在正确作出辅助线.
【变式8-3】(23-24八年级·江苏南通·阶段练习)如图,在平面直角坐标系中,点A(1,0),点B(2,0),点C,D是y轴上两个动点(点D在点C下方)且CD=2,连接AC,BD,则AC+BD的最小值为
【答案】
【分析】过A做y轴的平行线并截取AM=CD=2,做M关于y轴的对称点N,过N作NE⊥y轴,垂足为E.连接BN,然后在Rt△BNE中运用勾股定理即可解答.
【详解】解:将线段AC沿y轴方向向下平移两个单位,使C、D重合,设A点的对应点为AA1,连接AA1,作线段AA1关于y轴的对称线段EA2,连接BN交y轴于F,
由平移和对称的性质可得AC=DA1=AA2,EA2=AA1=2,
∵DA1+BD≥A2B
∴线段A2B的长即为AC+BD的最小值
∵在Rt△BA2E中,BE=2-(-1)=3,EA2=2
∴.
∴AC+BD的最小值为.
故填.
【点睛】本题主要考查了运用轴对称解决最短路径问题、坐标与图形、勾股定理等知识点,灵活运用轴对称知识和数形结合思想成为解答本题的关键.
21世纪教育网(www.21cnjy.com)
【人教版】
【题型1 垂线段最短】 1
【题型2 两点之间线段最短】 2
【题型3 平行线之间的距离】 4
【题型4 两动一定】 6
【题型5 两定一动(将军饮马)】 7
【题型6 两定两动型】 9
【题型7 两定一动(三点共线)】 10
【题型8 两动+定长】 11
知识点1:垂线段最短
【模型分析】
如图,点P在直线l外,过点P作l的垂线PH,则点P到直线l的距离为PH,即“垂线段最短”.
【温馨提示】解决最值问题常遵循:一找、二证、三计算.
【方法解读】
若所求线段不能直接利用“垂线段最短求最值”,需将其转化到定点和动点之间的线段,可借助矩形的对角线相等或全等三角形的性质.
【题型1 垂线段最短】
【例1】(23-24八年级·江苏盐城·期末)如图, 线段,是线段外一点,连接、,、分别是、的中点,连接、交于点.当四边形的面积为10时,线段的最小值为 .
【变式1-1】(23-24八年级·湖南娄底·阶段练习)如图,平分,于点E,F是射线上的任一点,,则的长度不可能是( )
A.4.2 B.5.15 C.3.69 D.8
【变式1-2】(23-24八年级·吉林·期中)如图,是一条河流,要铺设管道将河水引到两个用水点和,现有两种铺设管道的方案,若铺设管道单位长度的造价均相同,则下列说法正确的是( )
方案一:分别过,作的垂线,垂足为,,沿,铺设管道;
方案二:连接交于点,沿,铺设管道.
A.方案一与方案二一样省钱,因为管道长度一样
B.方案二比方案一省钱,因为两点之间,线段最短
C.方案一比方案二省钱,因为垂线段最短
D.方案一与方案二无法比较
【变式1-3】(23-24八年级·江西南昌·期末)如图,钝角的面积为12,最长边,平分,点M、N分别是上的动点,则的最小值是 .
【题型2 两点之间线段最短】
【例2】(23-24八年级·湖南郴州·期末)利用轴对称的性质解决路程之和最短的问题,如图所示,河岸的同侧有、两个村庄,两村委会决定在小河边建一座自来水加工厂向两村庄输送自来水,为了节约开支,加工厂建在何处所需铺设的管道最短?为什么?
【变式2-1】(23-24八年级·广东佛山·期末)如图所示,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资建一个蓄水池,不考虑其他因素,请画图确定蓄水池H点位置,使它与四个村庄的距离之和最小.
【变式2-2】(23-24八年级·陕西西安·期中)(1)如图1,在平面直角坐标系中,点的坐标分别为,现同时将点分别向上平移2个单位,再向右平移1个单位,分别得到点的对应点,连接,,直接写出点的坐标______,的坐标______及四边形的面积为______.
(2)如图2,A,B两单位分别位于一条封闭街道的两旁(直线是街道两边沿),现准备修建一座过街人行天桥.天桥应建在何处才能使由A经过天桥走到的路程最短?在图3中作出此时天桥的位置,简要叙述作法并保留作图痕迹(注:桥的宽度忽略不计,桥必须与街道垂直).
【变式2-3】(23-24六年级下·山东烟台·期中)如图,在同一平面内,点D、E是三角形外的两点,请按要求完成下列问题.
(1)请你判断线段与的大小关系是 ;理由是 ;
(2)①按要求将图形补充完整:连接线段,画射线、直线;
②若在四边形的边、、、上任取一点,分别为点K、L、M、N,并顺次连接它们,则四边形的周长 四边形的周长.(大于、小于或等于)
(3)在四边形内找一点O,使它到四边形四个顶点的距离之和最小.(保留作图痕迹,找到点即可)
【题型3 平行线之间的距离】
【例3】(23-24八年级·安徽合肥·期末)如图,,且相邻两条直线间的距离都是2,A,B,C分别为,,上的动点,连接AB、AC、BC,AC与交于点D,,则BD的最小值为( )
A.2 B.3 C.4 D.5
【变式3-1】(23-24八年级·北京海淀·期中)如图,在△ABC中,∠C=90°,BD为△ABC的角平分线,过点D作直线lAB,点P为直线l上的一个动点,若△BCD的面积为16,BC=8,则AP最小值为 .
【变式3-2】(23-24八年级·广东深圳·期末)如图,在四边形中,,,,面积为18,的垂直平分线分别交,于点,,若点和点分别是线段和边上的动点,则的最小值为 .
【变式3-3】(23-24八年级·福建龙岩·阶段练习)如图,在中,,,,D为的中点,E为线段上任意一点(不与端点重合),当E点在线段上运动时,则的最小值为 .
知识点2:两动一定
【模型分析】
问题:如图,直线AB、AC相交于点A,点M是平面内一点,点P,点N分别是AC,AB上一动点,求MP+PN的最小值.
解题思路:
一找:
第一步:作点M关于AC的对称点M′;
第二步:过点M′作M′N⊥AB于点N,交AC于点P;
二证:证明MP+PN的最小值为M′N:
三计算.
【题型4 两动一定】
【例4】(23-24八年级·广东珠海·期末)已知,在内有一定点P,点M,N分别是,上的动点,若的周长最小值为3,则的长为( )
A. B.3 C. D.
【变式4-1】(23-24八年级·安徽淮北·期末)如图,在中,,的面积为18,,平分,,分别是,上的动点,则的最小值为( )
A.4 B.6 C.7 D.9
【变式4-2】(23-24八年级·全国·专题练习)如图所示,在等边中,点D、E、F分别在边、,上,则线段的最小值是( )
A.边上高的长 B.线段的长度
C.边的长度 D.以上都不对
【变式4-3】(23-24八年级·湖南株洲·期中)如图,在等腰中,在、上分别截取、,使.再分别以点,为圆心,以大于的长为半径作弧,两弧在内交于点,作射线,交于点.已知,,.若点、分别是线段和线段上的动点,则的最小值为( )
A. B. C. D.
知识点3:两定一动
已知:在l上求作一点M,使得AM+BM最小.
【题型5 两定一动(将军饮马)】
【例5】(23-24八年级·宁夏银川·期末)如图,在中,,,,垂直平分,点P为直线上任意一点,则的最小值是 .
【变式5-1】(23-24八年级·广东揭阳·期末)如图,在长度为1个单位长度的小正方形组成的正方形网格中,点、、在小正方形的顶点上.
(1)在图中画出与关于直线成轴对称的.
(2)在直线上找一点,使的长最短.
【变式5-2】(23-24八年级·江西宜春·期末)如图,在中,边的垂直平分线交于点D,若,
(1)求的长;
(2)若点P是直线上的动点,直接写出的最小值为_________.
【变式5-3】(23-24八年级·河南周口·阶段练习)已知点P在内.
(1)如图①,点P关于射线的对称点分别是G、H,连接.
①若,则是什么特殊三角形?为什么?
②若,试判断与的数量关系,并说明理由;
(2)如图②,若, A、B分别是射线上的点,于点B,点P、Q分别为上的两个定点,且,,在上有一动点E,试求的最小值.
知识点4:两定两动
已知:在平面直角坐标系中,点P (2,3),Q (3,2),请在x轴和y轴上分别找到M点和N点,使四边形PQMN周长最小.作出M点和N点.
【题型6 两定两动型】
【例6】(23-24·福建莆田·中考模拟)如图,,,,、分别为、上的两个动点,则的最小值为______.
【变式6-1】(23-24八年级·江苏南京·期末)如图,在四边形ABCD中,∠BAD=∠B=∠D=90°,AD=AB=4,E是AD中点,M是边BC上的一个动点,N是边CD上的一个动点,则AM+MN+EN的最小值是 .
【变式6-2】(23-24八年级·河南安阳·阶段练习)如图,在矩形中,对角线上有两动点和,连接和,若,,则的最小值是( )
A.4 B.10 C.6 D.20
【变式6-3】(23-24八年级·广东江门·阶段练习)在中,分别为射线与射线上的两动点,且,连接,则最小值为 .
【题型7 两定一动(三点共线)】
【例7】(23-24八年级·浙江宁波·开学考试)如图,在中,,.延长线段至点,使,过点作射线,点为射线上的动点,分别过点,作直线的垂线,.当的值最大时,的度数为 .
【变式7-1】(23-24八年级·福建福州·期中)如图,在等边中,E是边的中点,P是的中线上的动点,且,则的最大值是 .
【变式7-2】(23-24八年级·湖北武汉·期末)如图,,在直线上方作等腰,,,连接,当最大时, .
【变式7-3】(23-24八年级·河北张家口·期末)如图,方格图中每个小正方形的边长为1,点A、B、C、M、N都在格点上.
(1)画出关于直线对称的;
(2)在直线上找点P使最小,在图形上画出点P的位置;
(3)在直线上找点Q使最大,直接写出这个最大值.
【题型8 两动+定长】
【例8】(23-24八年级·浙江绍兴·期末)如图,在平面直角坐标系中,,,,M,N是线段上的两个动点,且,则与周长和的最小值是 .
【变式8-1】(23-24八年级·全国·专题练习)如图,长方形中,,线段在边上左右滑动,若,则的最小值为 .
【变式8-2】(23-24八年级·湖北恩施·阶段练习)已知,如图,线段长为,于,于,,,为线段上两动点,在右侧且,则由到的路径:的最小值为 .
【变式8-3】(23-24八年级·江苏南通·阶段练习)如图,在平面直角坐标系中,点A(1,0),点B(2,0),点C,D是y轴上两个动点(点D在点C下方)且CD=2,连接AC,BD,则AC+BD的最小值为
21世纪教育网(www.21cnjy.com)
专题13.7 与轴对称图形有关的最值问题【八大题型】
【人教版】
【题型1 垂线段最短】 2
【题型2 两点之间线段最短】 5
【题型3 平行线之间的距离】 9
【题型4 两动一定】 13
【题型5 两定一动(将军饮马)】 17
【题型6 两定两动型】 23
【题型7 两定一动(三点共线)】 29
【题型8 两动+定长】 34
知识点1:垂线段最短
【模型分析】
如图,点P在直线l外,过点P作l的垂线PH,则点P到直线l的距离为PH,即“垂线段最短”.
【温馨提示】解决最值问题常遵循:一找、二证、三计算.
【方法解读】
若所求线段不能直接利用“垂线段最短求最值”,需将其转化到定点和动点之间的线段,可借助矩形的对角线相等或全等三角形的性质.
【题型1 垂线段最短】
【例1】(23-24八年级·江苏盐城·期末)如图, 线段,是线段外一点,连接、,、分别是、的中点,连接、交于点.当四边形的面积为10时,线段的最小值为 .
【答案】6
【分析】本题考查了三角形中线等分面积,垂线段最短,关键是由三角形面积公式求出的面积.
【详解】解:过作于,连接,延长交于,
、分别是、的中点,
的面积面积的一半,的面积面积的一半,
的面积的面积,
的面积四边形的面积,
、分别是、的中点,
的面积的面积,的面积的面积.
的面积的面积的面积的面积四边形的面积,
的面积,
的面积,
,
,
,
线段的最小值是6.
故答案为:6.
【变式1-1】(23-24八年级·湖南娄底·阶段练习)如图,平分,于点E,F是射线上的任一点,,则的长度不可能是( )
A.4.2 B.5.15 C.3.69 D.8
【答案】C
【分析】本题考查了角平分线的性质,垂线段最短等,过D点作于点H,根据角平分线的性质得到,再根据垂线段最短进行判断即可.
【详解】解:过D点作于点H,如图所示:
平分,
,
是射线上的任一点,
,
,
∴的长不能为3.69.
故选:C.
【变式1-2】(23-24八年级·吉林·期中)如图,是一条河流,要铺设管道将河水引到两个用水点和,现有两种铺设管道的方案,若铺设管道单位长度的造价均相同,则下列说法正确的是( )
方案一:分别过,作的垂线,垂足为,,沿,铺设管道;
方案二:连接交于点,沿,铺设管道.
A.方案一与方案二一样省钱,因为管道长度一样
B.方案二比方案一省钱,因为两点之间,线段最短
C.方案一比方案二省钱,因为垂线段最短
D.方案一与方案二无法比较
【答案】C
【分析】本题考查垂线段的性质,即垂线段最短.根据垂线段最短可得,,进而得出结论.解题的关键是掌握:垂线段最短指的是从直线外一点到这条直线所作的垂线段最短.实际问题中涉及线路最短问题时,其理论依据应从“两点之间,线段最短”和“垂线段最短”这两个中去选择.
【详解】解:∵,,
∴,,
∴,
∴按照方案一铺设管道的长度比按照方案二铺设管道的长度更短,
∵铺设管道单位长度的造价均相同,
∴方案一比方案二省钱.
故选:C.
【变式1-3】(23-24八年级·江西南昌·期末)如图,钝角的面积为12,最长边,平分,点M、N分别是上的动点,则的最小值是 .
【答案】3
【分析】本题考查了轴对称—最短路线问题,关键是画出符合条件的图形,题目具有一定的代表性,是一道比较好的题目.过点C作于点E,交于点M,过点M作于N,则当点C,M,N三点重合时,取得最小值,最小值为的长.再根据三角形的面积公式求出的长,即可.
【详解】解:过点C作于点E,交于点M,过点M作于N,
∵平分,,,
∴,
∴,
即当点C,M,N三点重合时,取得最小值,最小值为的长.
∵的面积为12,最长边,
∴,即,
∴
即的最小值为3.
故答案为:3.
【题型2 两点之间线段最短】
【例2】(23-24八年级·湖南郴州·期末)利用轴对称的性质解决路程之和最短的问题,如图所示,河岸的同侧有、两个村庄,两村委会决定在小河边建一座自来水加工厂向两村庄输送自来水,为了节约开支,加工厂建在何处所需铺设的管道最短?为什么?
【答案】见解析
【分析】此题主要考查了轴对称作图与应用设计,作点关于直线的对称点,连接,交直线于点,点即为所求;关键是正确找出点的位置.
【详解】解:如图,作点关于直线的对称点,连接,交直线于点,
由作图可知:,
要使的从点到点的路程最短,根据两点之间线段最短,连接,交直线于点,点即为所求;
故加工厂应该建在处.
【变式2-1】(23-24八年级·广东佛山·期末)如图所示,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资建一个蓄水池,不考虑其他因素,请画图确定蓄水池H点位置,使它与四个村庄的距离之和最小.
【答案】答案见解析
【分析】本题属于最短路线问题,解决此类题目的关键是掌握最有关短路径的知识点.
依据“两点之间线段最短”直接连接线段和,其交点H即为所求的点.
【详解】解:如下图所示,连接线段和,应把蓄水池建在交点上,因为这样H点既在线段上,又在线段上,由“两点之间,线段最短"可知,此时蓄水池与四个村庄的距离之和最小.
【变式2-2】(23-24八年级·陕西西安·期中)(1)如图1,在平面直角坐标系中,点的坐标分别为,现同时将点分别向上平移2个单位,再向右平移1个单位,分别得到点的对应点,连接,,直接写出点的坐标______,的坐标______及四边形的面积为______.
(2)如图2,A,B两单位分别位于一条封闭街道的两旁(直线是街道两边沿),现准备修建一座过街人行天桥.天桥应建在何处才能使由A经过天桥走到的路程最短?在图3中作出此时天桥的位置,简要叙述作法并保留作图痕迹(注:桥的宽度忽略不计,桥必须与街道垂直).
【答案】(1);8(2)见解析
【分析】本题考查坐标与图形性质;点的平移和三角形的面积,解答的关键得到四边形ACDB是平行四边形,
(1)根据点的平移规律即可得点C,D的坐标;由 即可计算出;
(2)沿竖直方向向下平移点A,使得平移的距离等于桥长,再根据两点之间线段最短,确定桥的位置即可;
【详解】解:(1)依题意,得,
∴;
(2)如图,将点A沿竖直向下的方向平移,平移距离等于桥长,到达点,连接,与街道交于点,过点建桥即符合要求;
【变式2-3】(23-24六年级下·山东烟台·期中)如图,在同一平面内,点D、E是三角形外的两点,请按要求完成下列问题.
(1)请你判断线段与的大小关系是 ;理由是 ;
(2)①按要求将图形补充完整:连接线段,画射线、直线;
②若在四边形的边、、、上任取一点,分别为点K、L、M、N,并顺次连接它们,则四边形的周长 四边形的周长.(大于、小于或等于)
(3)在四边形内找一点O,使它到四边形四个顶点的距离之和最小.(保留作图痕迹,找到点即可)
【答案】(1);两点之间线段最短
(2)①见解析;②小于
(3)见解析
【分析】本题考查直线、射线、线段等的作图以及两点之间、线段最短:
(1)根据两点之间线段最短判断即可;
(2)根据直线,射线,线段的定义以及题目要求作出图形即可;
(3)连接、,交于点,根据两点之间线段最短即可判断点即为所求.
解题的关键是理解直线,射线,线段的定义,灵活应用所学知识解决问题.
【详解】(1)解:根据两点之间线段最短得:,
故答案为:;两点之间线段最短.
(2)①如图所示,线段,射线、直线即为所求;
②如图:
,,,,
,即:四边形的周长小于四边形的周长,
故答案为:小于.
(3)连接、,交于点,
根据两点之间线段最短可知,,
即:此时点四边形四个顶点的距离之和最小,
如图所示,点即为所求.
【题型3 平行线之间的距离】
【例3】(23-24八年级·安徽合肥·期末)如图,,且相邻两条直线间的距离都是2,A,B,C分别为,,上的动点,连接AB、AC、BC,AC与交于点D,,则BD的最小值为( )
A.2 B.3 C.4 D.5
【答案】A
【分析】求BD的最小值可以转化为求点B到直线AC的距离,当BD⊥AC时,BD有最小值,根据题意求解即可.
【详解】解:由题意可知当BD⊥AC时,BD有最小值,
此时,AD=CD,∠ABC=90°,
∴BD=AD=BD=AC=2,
∴BD的最小值为2.
故选:A.
【点睛】本题考查平行线的性质,需结合图形,根据平行线的性质推出相关角的关系从而进行求解.
【变式3-1】(23-24八年级·北京海淀·期中)如图,在△ABC中,∠C=90°,BD为△ABC的角平分线,过点D作直线lAB,点P为直线l上的一个动点,若△BCD的面积为16,BC=8,则AP最小值为 .
【答案】4
【分析】根据三角形的面积公式求得CD,再根据角平分的性质求得DE,根据平行线之间的距离可得AP的最小值.
【详解】解:∵∠C=90°,△BCD的面积为16,BC=8,
∴,即,
作DE⊥AB,
∵BD为△ABC的角平分线,
∴,
∵直线lAB,
∴AP最小值与DE相等为4,
故答案为:4.
【点睛】本题考查角平分线的性质,平行线之间的距离,理解平行线之间距离的定义和点到直线的距离垂线段最短是解题关键.
【变式3-2】(23-24八年级·广东深圳·期末)如图,在四边形中,,,,面积为18,的垂直平分线分别交,于点,,若点和点分别是线段和边上的动点,则的最小值为 .
【答案】6
【分析】连接AQ,过点D作于H.利用三角形的面积公式求出DH,由题意得: ,求出AQ的最小值,AQ最小值是与DH相等,也就是时,根据面积公式求出DH的长度即可得到结论.
【详解】解:连接AQ,过点D作于H.
∵面积为18,BC=6,
∴,
∴,
∵MN垂直平分线段AB,
∴,
∴,
∴当AQ的值最小时,的值最小,
根据垂线段最短可知,当时,AQ的值最小,
∵,
∴AQ=DH=6,
∴的最小值为6.
故答案为:6.
【点睛】本题考查轴对称最短问题,平行线的性质,三角形的面积,线段的垂直平分线的性质等知识,把最短问题转化为垂线段最短是解题关键.
【变式3-3】(23-24八年级·福建龙岩·阶段练习)如图,在中,,,,D为的中点,E为线段上任意一点(不与端点重合),当E点在线段上运动时,则的最小值为 .
【答案】3
【分析】过C作,过C作,过D作的垂线交于点F交于点E,即可得到答案;
【详解】解:过C作,过D作的垂线交于点F,
∵,,,
∴,
∴即为最小值,
∵,,,
∴,,
∵,,
∴,
故答案为:3;
【点睛】本题考查角所对直角边等于斜边一半及平行线间距离处处相等且最短.
知识点2:两动一定
【模型分析】
问题:如图,直线AB、AC相交于点A,点M是平面内一点,点P,点N分别是AC,AB上一动点,求MP+PN的最小值.
解题思路:
一找:
第一步:作点M关于AC的对称点M′;
第二步:过点M′作M′N⊥AB于点N,交AC于点P;
二证:证明MP+PN的最小值为M′N:
三计算.
【题型4 两动一定】
【例4】(23-24八年级·广东珠海·期末)已知,在内有一定点P,点M,N分别是,上的动点,若的周长最小值为3,则的长为( )
A. B.3 C. D.
【答案】B
【分析】根据题意画出符合条件的图形,求出,得出等边三角形,求出,求出的周长,即可求出答案.
【详解】解:作P关于的对称点D,作P关于的对称点E,连接交于M,交于N,连接,则此时的周长最小,
连接,
∵P、D关于对称,
∴,
同理,
∴,
∵P、D关于对称,
∴,
∵,
∴,
同理,
∴,
∵,
∴是等边三角形,
∴,
∵的周长是,
∴
故选:B.
【点睛】本题考查了轴对称-最短路线问题,等边三角形的判定与性质,关键是画出符合条件的图形.
【变式4-1】(23-24八年级·安徽淮北·期末)如图,在中,,的面积为18,,平分,,分别是,上的动点,则的最小值为( )
A.4 B.6 C.7 D.9
【答案】A
【分析】过点C作于点P,交于点E,过点E作于F,则即为的最小值,再根据三角形的面积公式求出的长,即为的最小值.
【详解】解:过点C作于点P,交于点E,过点E作于F,
∵平分,,,
∴,
∴的最小值.
∵的面积为18,,
∴,
∴.
即的最小值为4,
故选:A.
【点睛】本题考查了轴对称-最短路线问题,关键是将的最小值为转化为,题目具有一定的代表性,是一道比较好的题目.
【变式4-2】(23-24八年级·全国·专题练习)如图所示,在等边中,点D、E、F分别在边、,上,则线段的最小值是( )
A.边上高的长 B.线段的长度
C.边的长度 D.以上都不对
【答案】A
【分析】作于点D,当、时,线段有最小值,根据等边三角形的性质可得,进而得结论.
【详解】解:如图,作于点D,当、时,线段有最小值,
∵是等边三角形,
∴,
∵,
∴,
∴,
∴,
∴线段的最小值是边上高的长.
故选:A.
【点睛】本题考查了轴对称-最短路线问题、等边三角形的性质,解决本题的关键是掌握等边三角形的性质.
【变式4-3】(23-24八年级·湖南株洲·期中)如图,在等腰中,在、上分别截取、,使.再分别以点,为圆心,以大于的长为半径作弧,两弧在内交于点,作射线,交于点.已知,,.若点、分别是线段和线段上的动点,则的最小值为( )
A. B. C. D.
【答案】C
【分析】本题考查了等腰三角形的性质,垂线段最短;过点B作于点H,交于点,根据等面积法,可得.作点H关于的对称点交于点N,连接,可得,进而可以解决问题.
【详解】解:如图,过点B作于点H,交于点,
由作图可知,平分,
∵,
∴,
∵,
∴,
∴.
∵,,
作点H关于的对称点交于点N,连接,
∴,
∴,
则的最小值为.
故选C.
知识点3:两定一动
已知:在l上求作一点M,使得AM+BM最小.
【题型5 两定一动(将军饮马)】
【例5】(23-24八年级·宁夏银川·期末)如图,在中,,,,垂直平分,点P为直线上任意一点,则的最小值是 .
【答案】4
【分析】由线段垂直平分线的性质可得,可得当点A,P,C在一条直线上时,有最小值,最小值为的长.
【详解】解:连接.
∵是的垂直平分线,
∴,
∴,
∴当点A,P,C在一条直线上时,有最小值,最小值为.
故答案为:4.
【点睛】本题考查了线段垂直平分线的性质,明确线段垂直平分线上的点到线段两端点的距离相等是解题的关键.
【变式5-1】(23-24八年级·广东揭阳·期末)如图,在长度为1个单位长度的小正方形组成的正方形网格中,点、、在小正方形的顶点上.
(1)在图中画出与关于直线成轴对称的.
(2)在直线上找一点,使的长最短.
【答案】(1)见解析
(2)见解析
【详解】(1)解:如图,△即为所求.
(2)如图,点即为所求.
【点睛】本题考查作图轴对称变换、轴对称最短路线问题,熟练掌握轴对称的性质是解答本题的关键.
【变式5-2】(23-24八年级·江西宜春·期末)如图,在中,边的垂直平分线交于点D,若,
(1)求的长;
(2)若点P是直线上的动点,直接写出的最小值为_________.
【答案】(1)9
(2)9
【分析】(1)根据垂直平分线的性质可证为等腰三角形,由角度可证为直角三角形,再由线段之间的关系即可求出的长;
(2)根据将军饮马原理即可得出的最小值为的长度.
【详解】(1)解:∵,
∴
∵边的垂直平分线交于点D,
∴,
∴
∴
在中,
∴
∴
(2)解:如图,
取点关于直线的对称点,即点;连接两点,与直线交于点,
根据两点之间线段最短
则即为的最小值,最小值为9
【点睛】本题考查了图形的轴对称,相关知识点有:垂直平分线的性质、将军饮马等,轴对称性质的充分利用是解题关键.
【变式5-3】(23-24八年级·河南周口·阶段练习)已知点P在内.
(1)如图①,点P关于射线的对称点分别是G、H,连接.
①若,则是什么特殊三角形?为什么?
②若,试判断与的数量关系,并说明理由;
(2)如图②,若, A、B分别是射线上的点,于点B,点P、Q分别为上的两个定点,且,,在上有一动点E,试求的最小值.
【答案】(1)①是等边三角形,理由见解析;②,理由见解析
(2)的最小值为5.
【分析】(1)①由轴对称的性质可得,,.根据“有一个角是的等腰三角形是等边三角形”即可得出是等边三角形;②当时,,G、O、H在同一直线上,由此可得与的数量关系;
(2)过Q作的对称点,连接,交于点E,连接,则的最小值为,由已知条件可得,易得,,由此可得是等边三角形,即可得的长,即的最小值.
【详解】(1)解:①是等边三角形,
∵点P关于对称的点为G,
∴,,
同理,,
∴,
∵,
∴,
∴是等边三角形.
②,
当时,,
∴G、O、H在同一直线上,.
∵,
∴;
(2)解:过Q作的对称点,连接,交于点E,连接,
∴ 最小值为.
∵,,
∴.
∵,,
∴,
∴,
∴.
∵点Q与关于对称,
∴,
∴,
∴是等边三角形,
∴,
即的最小值为5.
【点睛】本题主要考查了轴对称--最短路线问题,轴对称的性质和等边三角形的判定和性质.熟练掌握轴对称的性质及等边三角形的判定和性质,熟悉“将军饮马”模型是解题的关键.
知识点4:两定两动
已知:在平面直角坐标系中,点P (2,3),Q (3,2),请在x轴和y轴上分别找到M点和N点,使四边形PQMN周长最小.作出M点和N点.
【题型6 两定两动型】
【例6】(23-24·福建莆田·中考模拟)如图,,,,、分别为、上的两个动点,则的最小值为______.
【答案】
【解析】解:如图,连接,,
,,,
≌,
,
同理可得:,
,
当点,点,点,点共线时,有最小值,即最小值为的长度,
有最小值为,
故答案为:.
由“”可证≌,可得,,由,可得当点,点,点,点共线时,有最小值,即可求解.
本题考查了轴对称最短路线问题,全等三角形的判定和性质,证明,是本题的关键.
【变式6-1】(23-24八年级·江苏南京·期末)如图,在四边形ABCD中,∠BAD=∠B=∠D=90°,AD=AB=4,E是AD中点,M是边BC上的一个动点,N是边CD上的一个动点,则AM+MN+EN的最小值是 .
【答案】10
【分析】作A点关于BC的对称点A1,连接A1M,作E点关于DC的对称点E1,连接E1N,因此,所以最小值为,用勾股定理算出即可.
【详解】解:如图,作A点关于BC的对称点A1,连接A1M,作E点关于DC的对称点E1,连接E1N,
∵∠B=∠D=90°,点A和点A1关于BC对称,点E和点E1关于DC对称,
∴,,
∴,
∴AM+MN+EN的最小值是,
∵AD=AB=4,E是AD中点,
∴,,
∴,,
∵∠BAD=90°,
∴,
故答案为:10.
【点睛】本题考查了线段和的最值问题,勾股定理、轴对称性质,作出辅助线是本题的关键.
【变式6-2】(23-24八年级·河南安阳·阶段练习)如图,在矩形中,对角线上有两动点和,连接和,若,,则的最小值是( )
A.4 B.10 C.6 D.20
【答案】B
【分析】如图,连接,,由全等三角形判定可以证得,得到,进而得到,再根据题意及勾股定理求出的值,即可得出答案.
【详解】解:如图,连接,,
四边形是矩形,
,,,
,
,
,
,
,
,
又 ,为矩形的对角线,
,
是直角三角形,,
,
解得,或
,则不符合题意,
,
,
故选B.
【点睛】本题考查了矩形的性质,全等三角形的判定与性质,两点之间线段最短,勾股定理的应用及解一元二次方程,熟知相关的判定与性质及解一元二次方程的方法是解题关键.
【变式6-3】(23-24八年级·广东江门·阶段练习)在中,分别为射线与射线上的两动点,且,连接,则最小值为 .
【答案】
【分析】本题考查了全等三角形的性质与判定以及勾股定理;过点作,使得,过点作于点,连接,证明得出 ,则当在线段上时,取的最小值,最小值为的长,
【详解】解:如图,过点作,使得,过点作于点,连接,
在中,
,
∴,
∴,
∴,
则当在线段上时,取的最小值,最小值为的长,
∵,,,
∴
∵,
∴,
在中,,
∴,
∴,
故答案为:.
【题型7 两定一动(三点共线)】
【例7】(23-24八年级·浙江宁波·开学考试)如图,在中,,.延长线段至点,使,过点作射线,点为射线上的动点,分别过点,作直线的垂线,.当的值最大时,的度数为 .
【答案】/130度
【分析】本题考查了全等三角形的判定和性质,平行线的性质,等腰三角形的判定和性质.如图,过点作直线于点.证明,推出与重合时,的值最大,此时,画出相应的图形,根据条件,利用三角形的内角和、邻补角的意义,求出结果.
【详解】解:如图,过点作直线于点.
直线,直线,
,
,,
,
,
,
与重合时,的值最大,
当与重合,与重合时,的值最大,此时,
,
,
,
,
,
又,
,
,
故答案为:.
【变式7-1】(23-24八年级·福建福州·期中)如图,在等边中,E是边的中点,P是的中线上的动点,且,则的最大值是 .
【答案】3
【分析】连接PC,则BP=CP,=CP-PE,当点P与点A重合时,CP-PE=CE,进而即可求解.
【详解】解:连接PC,
∵在等边中,,P是的中线上的动点,
∴AD是BC的中垂线,
∴BP=CP,
∴=CP-PE,
∵在中,CP-PE<CE,
∴当点P与点A重合时,CP-PE=CE,
∵E是边的中点,
∴的最大值=6÷2=3.
故答案是:3.
【点睛】本题主要考查等边三角形的性质,三角形三边长关系,连接CP,得到=CP-PE,是解题的关键.
【变式7-2】(23-24八年级·湖北武汉·期末)如图,,在直线上方作等腰,,,连接,当最大时, .
【答案】
【分析】构造等腰,如图1,使,,则,,当、、三点共线时,最大,然后根据已知角及等腰三角形的性质即可求解.
【详解】解:如图1,构造等腰,使,,
则,,
∴当、、共线时,最大,
此时,如图2所示,
,,则,
∴,
∵,,
∴,
∴.
故答案为:45°.
【点睛】本题主要考查了等腰三角形的性质、三角形全等的判定和性质,解题的关键是准确作出辅助线,找出当最大时的图形.
【变式7-3】(23-24八年级·河北张家口·期末)如图,方格图中每个小正方形的边长为1,点A、B、C、M、N都在格点上.
(1)画出关于直线对称的;
(2)在直线上找点P使最小,在图形上画出点P的位置;
(3)在直线上找点Q使最大,直接写出这个最大值.
【答案】(1)见解析
(2)见解析
(3)作图见解析;最大值为3
【分析】(1)利用网格特点,先画出A、B、C关于直线的对称点、、,再顺次连接即可;
(2)作点C关于的对称点D,连接交于一点,该点即为点P;
(3)由于,则,而由三角形的三边关系可得,当Q、、B三点共线时取等号,从而可得答案.
【详解】(1)解:即为所求作的三角形,如图所示:
(2)解:如图,作点C关于的对称点D,连接交于一点,该点即为所求作的点P;
∵点C与D关于的对称,
∴,
∴,
∵,只有当点P、B、D三点共线时等号成立,
∴当点P、B、D三点共线时,最小,即最小;
(3)解:先作出A关于直线的对称点,连接并延长交于一点,该点即为点Q,如图所示:
∵,
∴,
根据三角形的三边关系可得,当Q、、B三点共线时取等号,
∴的最大值为.
【点睛】本题主要考查了作图—轴对称变换、轴对称的性质和三角形的三边关系,属于常考题型,熟练掌握上述知识是解题的关键.
【题型8 两动+定长】
【例8】(23-24八年级·浙江绍兴·期末)如图,在平面直角坐标系中,,,,M,N是线段上的两个动点,且,则与周长和的最小值是 .
【答案】
【分析】将点C项左平移2个单位得到,找出点A关于x轴的对称点,连接交x轴于一点即为最短距离点,根据勾股定理即可得到答案;
【详解】解:由题意可得,
,
∵,,,
∴当最小即可得到答案,
点C项左平移2个单位得到,找出点A关于x轴的对称点,连接交x轴于一点即为最短距离点,如图所示,
根据勾股定理可得,
,
∴与周长和的最小值是:,
故答案为:.
【点睛】本题考查最短距离问题及勾股定理,解题的关键是根据轴对称的性质及两点间线段距离最短得到最小距离位置.
【变式8-1】(23-24八年级·全国·专题练习)如图,长方形中,,线段在边上左右滑动,若,则的最小值为 .
【答案】
【分析】取,作关于的对称点,连接,得出四边形是平行四边形,继而可得 ,当三点共线时,最小,最小值为,勾股定理即可求解.
【详解】解:如图,取,作关于的对称点,连接,
∴,
∵,
∴四边形是平行四边形,
∴,
∴ ,
∴当三点共线时,最小,最小值为,
此时,
在中,,
即的最小值为,
故答案为:.
【点睛】本题考查了勾股定理,轴对称求线段和的最值问题,掌握轴对称的性质是解题的关键.
【变式8-2】(23-24八年级·湖北恩施·阶段练习)已知,如图,线段长为,于,于,,,为线段上两动点,在右侧且,则由到的路径:的最小值为 .
【答案】/
【分析】过点作且,作关于的对称点,连接交于点,连接交于点,过点作交于,证明,再根据全等三角形的性质,得出,再根据轴对称的性质,得出,进而得出,再根据两点之间线段最短,得出的最小值为的长,此时,的值最小,过点作交的延长线于,再根据线段之间的数量关系,得出,,再根据勾股定理,得出,进而即可得出答案.
【详解】解:过点作且,作关于的对称点,连接交于点,连接交于点,过点作交于,
∵,
∴,
∵,,
∴,
∴,
∵关于的对称点,
∴,
∴,
∴,
∴的最小值为的长,此时,的值最小,
过点作交的延长线于,
∴,
∵,
∴,
∴,
∴的最小值为.
故答案为:
【点睛】本题考查了全等三角形的判定与性质、轴对称的性质、两点之间线段最短、勾股定理,解本题的关键在正确作出辅助线.
【变式8-3】(23-24八年级·江苏南通·阶段练习)如图,在平面直角坐标系中,点A(1,0),点B(2,0),点C,D是y轴上两个动点(点D在点C下方)且CD=2,连接AC,BD,则AC+BD的最小值为
【答案】
【分析】过A做y轴的平行线并截取AM=CD=2,做M关于y轴的对称点N,过N作NE⊥y轴,垂足为E.连接BN,然后在Rt△BNE中运用勾股定理即可解答.
【详解】解:将线段AC沿y轴方向向下平移两个单位,使C、D重合,设A点的对应点为AA1,连接AA1,作线段AA1关于y轴的对称线段EA2,连接BN交y轴于F,
由平移和对称的性质可得AC=DA1=AA2,EA2=AA1=2,
∵DA1+BD≥A2B
∴线段A2B的长即为AC+BD的最小值
∵在Rt△BA2E中,BE=2-(-1)=3,EA2=2
∴.
∴AC+BD的最小值为.
故填.
【点睛】本题主要考查了运用轴对称解决最短路径问题、坐标与图形、勾股定理等知识点,灵活运用轴对称知识和数形结合思想成为解答本题的关键.
21世纪教育网(www.21cnjy.com)
