人教版2024-2025学年八年级数学上册举一反三专题13.1轴对称【十大题型】(学生版+解析)
文档属性
| 名称 | 人教版2024-2025学年八年级数学上册举一反三专题13.1轴对称【十大题型】(学生版+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 14:30:29 | ||
图片预览



文档简介
专题13.1 轴对称【十大题型】
【人教版】
【题型1 识别轴对称图形】 1
【题型2 确定对称轴的条数】 2
【题型3 由轴对称图形的特征进行判断】 3
【题型4 由轴对称图形的特征进行求解】 4
【题型5 折叠问题】 5
【题型6 镜面对称】 6
【题型7 画轴对称图形】 7
【题型8 台球桌上的轴对称】 8
【题型9 添加图形使成为轴对称图形】 10
【题型10 设计轴对称图案】 11
知识点1:轴对称
(1)轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴
对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称.
(2)轴对称图形是针对一个图形而言的,是一种具有特殊性质图形,被一条直线分割成的两部分沿着对称
轴折叠时,互相重合;轴对称图形的对称轴可以是一条,也可以是多条甚至无数条.
【题型1 识别轴对称图形】
【例1】(23-24八年级·黑龙江哈尔滨·阶段练习)下列图形中,不是轴对称图形的是( ).
A. B. C. D.
【变式1-1】(23-24八年级·广东广州·期末)下列图形中,是轴对称图形的是( )
A.平行四边形 B.直角梯形 C.正五边形 D.直角三角形
【变式1-2】(23-24八年级·吉林四平·期末)下列三角形中,不是轴对称图形的是( )
A.有两个角相等的三角形
B.有两个角分别是120°和30°的三角形
C.有一个角是45°的直角三角形
D.有一个角是60°的直角三角形
【变式1-3】(23-24八年级·重庆南岸·期末)图是的正方形网格,每个小正方形的顶点称为格点.其中点均在格点上.请在给定的网格中,找一格点,使以点为顶点的四边形是轴对称图形,满足条件的点的个数是 个.
知识点2:轴对称的性质
(1)如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
由轴对称的性质得到一下结论:
①如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称;
②如果两个图形成轴对称,我们只要找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这
两个图形的对称轴.
(2)轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
【题型2 确定对称轴的条数】
【例2】(23-24八年级·江苏宿迁·期末)在等腰直角三角形、等边三角形、半圆、正方形这四种常见的轴对称图形中,对称轴最多的是 .
【变式2-1】(23-24八年级·山东烟台·期末)下列图形中是轴对称图形,且对称轴只有两条的是( )
A. B. C. D.
【变式2-2】(23-24八年级·黑龙江大庆·期中)要使大小两个圆组合成的图形有无数条对称轴,应采用第( )种画法
A. B. C. D.
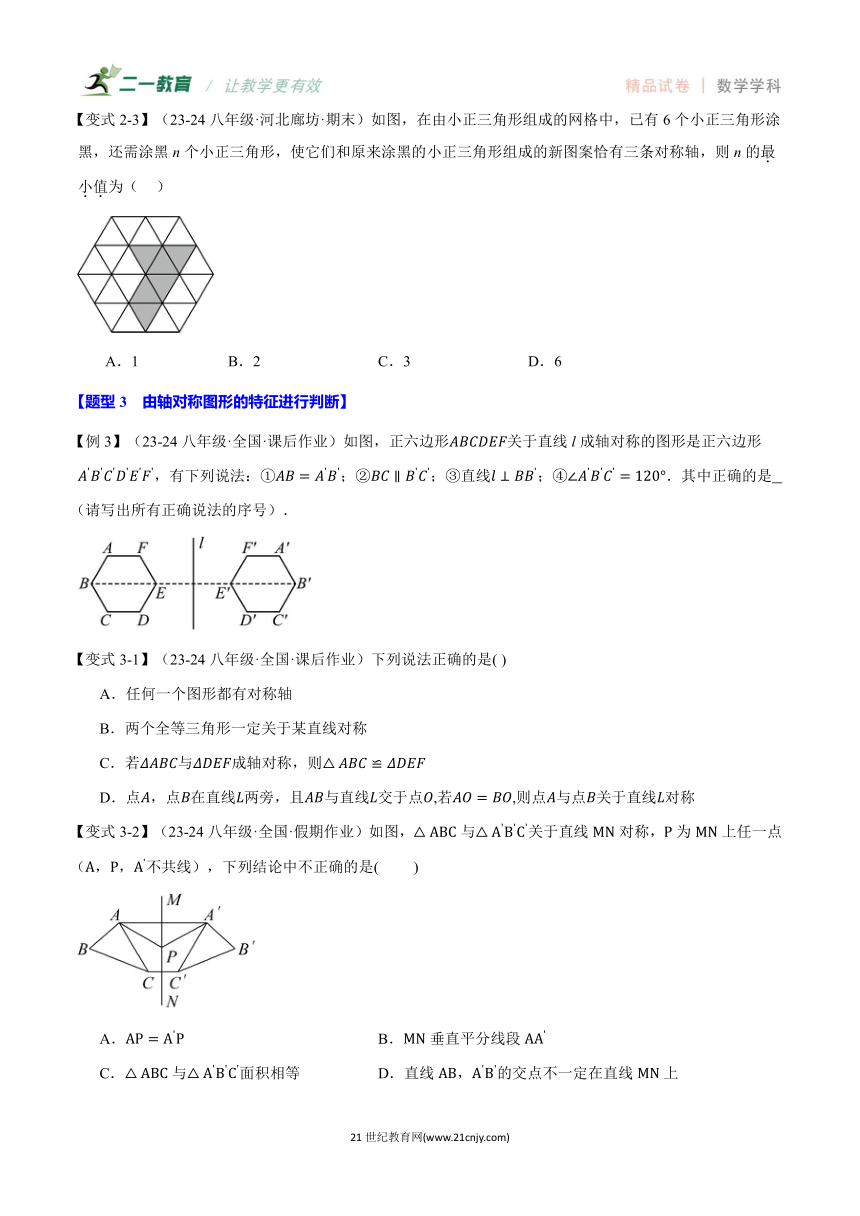
【变式2-3】(23-24八年级·河北廊坊·期末)如图,在由小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑n个小正三角形,使它们和原来涂黑的小正三角形组成的新图案恰有三条对称轴,则n的最小值为( )
A.1 B.2 C.3 D.6
【题型3 由轴对称图形的特征进行判断】
【例3】(23-24八年级·全国·课后作业)如图,正六边形关于直线l成轴对称的图形是正六边形,有下列说法:①;②;③直线;④.其中正确的是 (请写出所有正确说法的序号).
【变式3-1】(23-24八年级·全国·课后作业)下列说法正确的是( )
A.任何一个图形都有对称轴
B.两个全等三角形一定关于某直线对称
C.若与成轴对称,则
D.点,点在直线两旁,且与直线交于点,若,则点与点关于直线对称
【变式3-2】(23-24八年级·全国·假期作业)如图,与关于直线对称,为上任一点(,,不共线),下列结论中不正确的是( )
A. B.垂直平分线段
C.与面积相等 D.直线,的交点不一定在直线上
【变式3-3】(23-24八年级·全国·课后作业)一个图形沿一条直线翻折后再沿这条直线的方向平移,我们把这样的图形运动称为图形的翻移,这条直线称为翻移线.如图△A2B2C2是由△ABC沿直线l翻移后得到的.在下列结论中,图形的翻移所具有的性质是( )
A.各对应点之间的距离相等 B.各对应点的连线互相平行
C.对应点连线被翻移线平分 D.对应点连线与翻移线垂直
【题型4 由轴对称图形的特征进行求解】
【例4】(23-24八年级·辽宁沈阳·期末)如图,AD所在直线是△ABC的对称轴,点E,F是AD上的两点,若BD=3,AD=5,则图中阴影部分的面积是 .
【变式4-1】(23-24八年级·浙江杭州·开学考试)如图所示的2×2方格中,连接AB,AC,AD,则∠A+∠B+∠C的和( ).
A.必是直角 B.必是锐角 C.必是钝角 D.是锐角或钝角
【变式4-2】(23-24八年级·全国·假期作业)如图,O为内部一点,,P、R为O分别以直线、为对称轴的对称点.
(1)请指出当是什么角度时,会使得的长度等于7?并完整说明的长度为何在此时等于7的理由.
(2)承(1)小题,请判断当不是你指出的角度时,的长度小于7还是大于7?并完整说明你判断的理由.
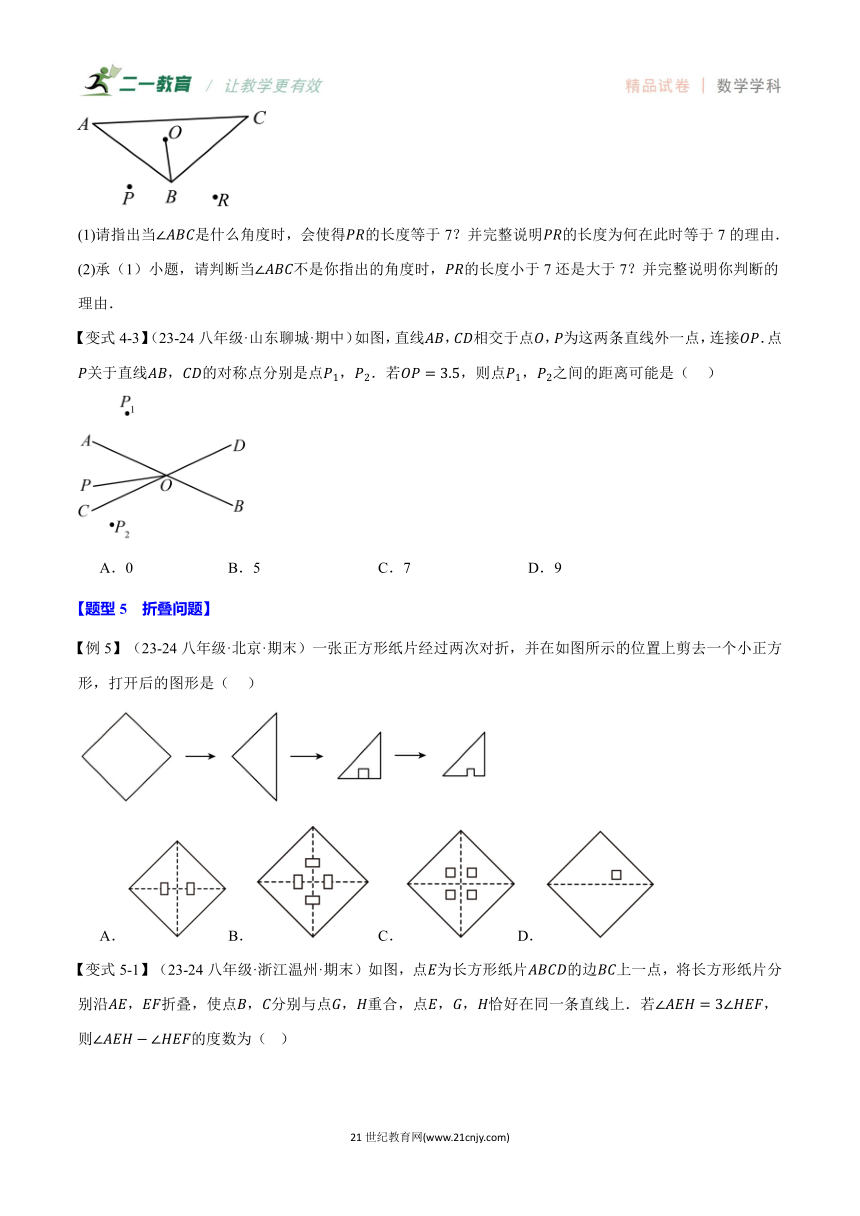
【变式4-3】(23-24八年级·山东聊城·期中)如图,直线,相交于点,为这两条直线外一点,连接.点关于直线,的对称点分别是点,.若,则点,之间的距离可能是( )
A.0 B.5 C.7 D.9
【题型5 折叠问题】
【例5】(23-24八年级·北京·期末)一张正方形纸片经过两次对折,并在如图所示的位置上剪去一个小正方形,打开后的图形是( )
A.B. C.D.
【变式5-1】(23-24八年级·浙江温州·期末)如图,点为长方形纸片的边上一点,将长方形纸片分别沿,折叠,使点,分别与点,重合,点,,恰好在同一条直线上.若,则的度数为( )
A. B. C. D.
【变式5-2】(23-24八年级·云南昆明·开学考试)一个长8厘米,宽5厘米的长方形纸片,沿对角线对折后,得到下面所示几何图形,阴影部分的周长是 厘米.
【变式5-3】(23-24八年级·陕西西安·期末)将如图(1)所示的长方形纸片按如下步骤操作:(1)如图(2),以过点A的直线为对称轴折叠纸片,使点B恰好落在边上的点处,折痕与交于点E;(2)如图(3),以过点E的直线为对称轴折叠纸片,使点A恰好落在边上的点处,折痕交边于点F;(3)将纸片展平.那么的度数为 .
【题型6 镜面对称】
【例6】(23-24八年级·贵州遵义·期末)如图是一只停放在平静水面上的小船,则它在水中的倒影表示正确的是( )
A. B.
C. D.
【变式6-1】(23-24八年级·河南许昌·期中)小明照镜子的时候,发现T恤上的英文单词 APPLE在镜子中呈现的样子( )
A. B. C. D.
【变式6-2】(23-24八年级·内蒙古呼和浩特·期中)小明在镜中看到身后墙上的时钟如下,你认为实际时间最接近9:00( )
A.B.C.D.
【变式6-3】(23-24八年级·福建龙岩·阶段练习)在平面镜里看到背后墙上的电子钟示数如图所示,这时的实际时间应是 .
【题型7 画轴对称图形】
【例7】(23-24八年级·山东枣庄·期末)如图,的三个顶点分别位于正方形网格线的交点上,我们把称为格点三角形,请你分别在图①,图②,图③的正方形网格中作一个格点三角形与成轴对称(所作图形不能重复),并画出对称轴.
【变式7-1】(23-24八年级·陕西西安·期末)如图,方格纸中每个小正方形的边长均为,的顶点都在小正方形的顶点上,
(1)在图中画出,使与关于所在直线对称,点与点是对称点;
(2)求四边形的面积.
【变式7-2】(23-24八年级·山东济南·期末)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.已知的顶点均在格点上.
(1)画出格点三角形关于直线对称的;
(2)的面积是
(3)在直线上找出点P,使最大,并求出最大值为 .(保留作图痕迹)
【变式7-3】(23-24八年级·全国·假期作业)如图1,在的网格中,三个顶点均在格点上,这样的三角形叫做“格点三角形”.在图中画出一个“格点三角形”(阴影部分)与原关于某条直线成轴对称.请在图2、图3、图4中,各画一个和原三角形成轴对称的“格点三角形”,并将所画的“格点三角形”用“斜线”涂成“阴影部分”(图图4不重复).
【题型8 台球桌上的轴对称】
【例8】(23-24八年级·山东德州·期中)如图,桌球的桌面上有M,N两个球,若要将M球射向桌面的一边,反弹一次后击中N球,则A,B,C,D,4个点中,可以反弹击中N球的是 点.
【变式8-1】(23-24八年级·江苏苏州·阶段练习)如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是 ( )
A.点A B.点B C.点C D.点D
【变式8-2】(23-24八年级·全国·课堂例题)如图所示,长方形是台球台面,有白、黑两球分别位于点M,N处,试问:怎样撞击白球M,才能使白球M碰撞台边反弹后击中黑球N?
【变式8-3】(23-24八年级·江苏常州·期中)如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到矩形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到矩形的边时的点为Q,第2次碰到矩形的边时的点为M,….第2022次碰到矩形的边时的点为图中的( )
A.点P B.点Q C.点M D.点N
【题型9 添加图形使成为轴对称图形】
【例9】(2024·河北石家庄·模拟预测)如图所示的方格纸,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个被涂黑的图案构成一个轴对称图形,那么涂法共有( )种.
A.6 B.5 C.4 D.3
【变式9-1】(23-24八年级·河南安阳·期末)(1)如图,在由小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑2个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰为轴对称图形.请在下图中画出两种不同的填涂方案设计,并用虚线标出对称轴;
【变式9-2】(23-24八年级·山东聊城·期中)乐乐觉得轴对称图形很有意思,如图是4个完全相同的小正方形组成的形图,请你用三种方法分别在图中添画一个小正方形,使添画后的图形成为轴对称图形.
【变式9-3】(23-24八年级·江苏无锡·期中)在4×4的方格中有五个同样大小的正方形如图摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有 种.
【题型10 设计轴对称图案】
【例10】(23-24八年级·河北保定·期中)如图,是由4×4个大小完在一样的小正方形组成的方格纸,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)
【变式10-1】(23-24八年级·江苏扬州·期末)如图1是3×3的正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,(要求:绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图2中的两幅图就视为同一种图案),请在图3中的四幅图中完成你的设计.
【变式10-2】(23-24八年级·甘肃平凉·期末)如图所示,
(1)观察图①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征:
(2)借助图⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所给出的两个共同特征.(注意:新图案与图①~④的图案不能重合)
【变式10-3】(2024·山东枣庄·中考真题)(1)观察分析:在一次数学综合实践活动中,老师向同学们展示了图①,图②,图③三幅图形,请你结合自己所学的知识,观察图中阴影部分构成的图案,写出三个图案都具有的两个共同特征:___________,___________.
(2)动手操作:请在图④中设计一个新的图案,使其满足你在(1)中发现的共同特征.
21世纪教育网(www.21cnjy.com)
专题13.1 轴对称【十大题型】
【人教版】
【题型1 识别轴对称图形】 1
【题型2 确定对称轴的条数】 3
【题型3 由轴对称图形的特征进行判断】 5
【题型4 由轴对称图形的特征进行求解】 8
【题型5 折叠问题】 11
【题型6 镜面对称】 14
【题型7 画轴对称图形】 16
【题型8 台球桌上的轴对称】 19
【题型9 添加图形使成为轴对称图形】 22
【题型10 设计轴对称图案】 24
知识点1:轴对称
(1)轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴
对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称.
(2)轴对称图形是针对一个图形而言的,是一种具有特殊性质图形,被一条直线分割成的两部分沿着对称
轴折叠时,互相重合;轴对称图形的对称轴可以是一条,也可以是多条甚至无数条.
【题型1 识别轴对称图形】
【例1】(23-24八年级·黑龙江哈尔滨·阶段练习)下列图形中,不是轴对称图形的是( ).
A. B. C. D.
【答案】B
【分析】根据轴对称图形的定义,一个图形沿着一条直线折叠,直线两旁的部分能够相互重合,那么这个图形叫做轴对称图形,对选项进行分析判断即可.
【详解】解:选项、、中的图形都能找到对称轴,使得对称轴两旁的部分能够相互重合,都是轴对称图形,选项中的图形,没有对称轴可以使对称轴两旁的部分能够相互重合,不是轴对称图形,
故选:.
【点睛】本题考查轴对称图形,解答本题的关键是明确轴对称图形的定义,一个图形沿着一条直线折叠,直线两旁的部分能够相互重合,那么这个图形叫做轴对称图形.
【变式1-1】(23-24八年级·广东广州·期末)下列图形中,是轴对称图形的是( )
A.平行四边形 B.直角梯形 C.正五边形 D.直角三角形
【答案】C
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
【详解】解:A、平行四边形不是轴对称图形,故本选项不合题意;
B、直角梯形不是轴对称图形,故本选项不合题意;
C、正五边形是轴对称图形,故本选项符合题意;
D、直角三角形不是轴对称图形,故本选项不合题意.
故选:C.
【点睛】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
【变式1-2】(23-24八年级·吉林四平·期末)下列三角形中,不是轴对称图形的是( )
A.有两个角相等的三角形
B.有两个角分别是120°和30°的三角形
C.有一个角是45°的直角三角形
D.有一个角是60°的直角三角形
【答案】D
【分析】根据轴对称图形的概念求解.直角三角形中只有等腰直角三角形是轴对称图形.
如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
【详解】解:根据轴对称图形的定义:
A、有两个内角相等的三角形,是轴对称图形,不符合题意;
B、有两个角分别是120°和30°的三角形,另一个内角也是30°,故是轴对称图形,不符合题意;
C、有一个内角为45°的直角三角形,是轴对称图形,不符合题意
D、有一个角是60°的直角三角形,找不到对称轴,则不是轴对称图形,符合题意.
故选D.
【点睛】本题考查轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
【变式1-3】(23-24八年级·重庆南岸·期末)图是的正方形网格,每个小正方形的顶点称为格点.其中点均在格点上.请在给定的网格中,找一格点,使以点为顶点的四边形是轴对称图形,满足条件的点的个数是 个.
【答案】2
【分析】根据轴对称图形的定义,动手逐个判断即可求解.
【详解】解:如图所示,
即:满足条件的点的个数为2个,
故答案为:2.
【点睛】本题主要考查了轴对称图形,熟练掌握轴对称图形的定义:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形是解题的关键.
知识点2:轴对称的性质
(1)如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
由轴对称的性质得到一下结论:
①如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称;
②如果两个图形成轴对称,我们只要找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这
两个图形的对称轴.
(2)轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
【题型2 确定对称轴的条数】
【例2】(23-24八年级·江苏宿迁·期末)在等腰直角三角形、等边三角形、半圆、正方形这四种常见的轴对称图形中,对称轴最多的是 .
【答案】正方形
【分析】本题考查了求对称轴条数,分别写出各个图形的对称轴的条数,比较即可得出答案.
【详解】解:等腰直角三角形有条对称轴;
等边三角形有条对称轴;
半圆由条对称轴;
正方形有条对称轴;
∴对称轴最多的是正方形,
故答案为:正方形.
【变式2-1】(23-24八年级·山东烟台·期末)下列图形中是轴对称图形,且对称轴只有两条的是( )
A. B. C. D.
【答案】A
【分析】本题考查了轴对称图形的识别,解题的关键是掌握一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形是轴对称图形,这条直线是对称轴.
【详解】解:A、是轴对称图形,有2条对称轴,符合题意;
B、是轴对称图形,有1条对称轴,不符合题意;
C、不是轴对称图形,不符合题意;
D、是轴对称图形,有8条对称轴,不符合题意;
故选:A.
【变式2-2】(23-24八年级·黑龙江大庆·期中)要使大小两个圆组合成的图形有无数条对称轴,应采用第( )种画法
A. B. C. D.
【答案】B
【分析】此题考查轴对称图形定义及对称轴的条数,一个图形沿某条直线对折,直线两旁的部分能够完全重合,这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴.
【详解】解:在给出的选项中的图形中,A ,C ,D有1条对称轴,B 有无数条对称轴.
所以要使大小两个圆有无数条对称轴,应采用B画法.
故选:B.
【变式2-3】(23-24八年级·河北廊坊·期末)如图,在由小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑n个小正三角形,使它们和原来涂黑的小正三角形组成的新图案恰有三条对称轴,则n的最小值为( )
A.1 B.2 C.3 D.6
【答案】C
【分析】本题考查了利用轴对称设计图案,解题的关键是掌握常见图形的性质和轴对称图形的性质.由等边三角形有三条对称轴可得答案.
【详解】解:如图所示,n的最小值为3.
故选:C.
【题型3 由轴对称图形的特征进行判断】
【例3】(23-24八年级·全国·课后作业)如图,正六边形关于直线l成轴对称的图形是正六边形,有下列说法:①;②;③直线;④.其中正确的是 (请写出所有正确说法的序号).
【答案】①③④
【分析】根据轴对称的性质,多边形的内角和求解,然后判断作答即可.
【详解】解:由轴对称的性质可得,,直线,,
∴①③④正确,故符合要求;②错误,故不符合要求;
故答案为:①③④.
【点睛】本题考查了轴对称的性质,多边形的内角和.解题的关键在于对知识的熟练掌握与灵活运用.
【变式3-1】(23-24八年级·全国·课后作业)下列说法正确的是( )
A.任何一个图形都有对称轴
B.两个全等三角形一定关于某直线对称
C.若与成轴对称,则
D.点,点在直线两旁,且与直线交于点,若,则点与点关于直线对称
【答案】C
【分析】根据轴对称的定义:两个图形沿一条直线对着,直线两旁的部分能完全重合,那么这两个图形成轴对称进行判断即可.
【详解】A.有的图形没有对称轴,该选项错误;
B.由于位置关系不明确,如图一,该选项错误,
C. 若与成轴对称,则,该选项正确;
D、因为线段与直线不一定垂直,所以不能正确判定,该选项错误.
故选:C.
【点睛】本题主要考查了轴对称图形,关键是熟练把握轴对称的定义.
【变式3-2】(23-24八年级·全国·假期作业)如图,与关于直线对称,为上任一点(,,不共线),下列结论中不正确的是( )
A. B.垂直平分线段
C.与面积相等 D.直线,的交点不一定在直线上
【答案】D
【分析】利用轴对称的性质解答.
【详解】解:与关于直线对称,为上任意一点,
垂直平分,
∴,与面积相等,故,,选项不符合题意;
直线,关于直线对称,因此交点一定在上,故D选项符合题意,
故选:D.
【点睛】此题考查轴对称的性质:轴对称图形的对应角相等,对应边相等,轴对称的三角形全等由此面积相等.
【变式3-3】(23-24八年级·全国·课后作业)一个图形沿一条直线翻折后再沿这条直线的方向平移,我们把这样的图形运动称为图形的翻移,这条直线称为翻移线.如图△A2B2C2是由△ABC沿直线l翻移后得到的.在下列结论中,图形的翻移所具有的性质是( )
A.各对应点之间的距离相等 B.各对应点的连线互相平行
C.对应点连线被翻移线平分 D.对应点连线与翻移线垂直
【答案】C
【分析】根据图象的翻折和平移的性质得出对应点连线被翻移线平分.
【详解】∵如图所示:△A2B2C2是由△ABC沿直线l翻移后得到的,
∴图形的翻移所具有的性质是:对应点连线被翻移线平分.
故选C.
【点睛】此题主要考查了几何变换的类型,根据翻折和平移的性质得出是解题关键.
【题型4 由轴对称图形的特征进行求解】
【例4】(23-24八年级·辽宁沈阳·期末)如图,AD所在直线是△ABC的对称轴,点E,F是AD上的两点,若BD=3,AD=5,则图中阴影部分的面积是 .
【答案】
【分析】根据△CEF和△BEF关于直线AD对称,得出S△BEF=S△CEF,根据图中阴影部分的面积是S△ABC求出即可.
【详解】解:∵△ABC关于直线AD对称,
∴B、C关于直线AD对称,
∴△CEF和△BEF关于直线AD对称,
∴S△BEF=S△CEF,
∵△ABC的面积是:×BC×AD=×6×5=15,
∴图中阴影部分的面积是S△ABC=.
故答案为:.
【点睛】本题考查了轴对称的性质.通过观察可以发现是轴对称图形,且阴影部分的面积为全面积的一半,根据轴对称图形的性质求解.其中看出三角形BEF与三角形CEF关于AD对称,面积相等是解决本题的关键.
【变式4-1】(23-24八年级·浙江杭州·开学考试)如图所示的2×2方格中,连接AB,AC,AD,则∠A+∠B+∠C的和( ).
A.必是直角 B.必是锐角 C.必是钝角 D.是锐角或钝角
【答案】C
【分析】观察图形可知该图形关于线段AC所在的直线对称,从而得到∠1+∠3=90°,∠2=45°,从而求得三个角的和.
【详解】解:∵2×2正方格关于线段AC所在的直线对称,
∴∠1=∠4,
∵∠4+∠3=90°,∠2=45°,
∴∠1+∠2+∠3=90°+45°=135°.
故选:C.
【点睛】本题考查了轴对称的性质,角度的计算,以及角的分类,解题的关键是发现本图关于线段AC所在的直线对称.
【变式4-2】(23-24八年级·全国·假期作业)如图,O为内部一点,,P、R为O分别以直线、为对称轴的对称点.
(1)请指出当是什么角度时,会使得的长度等于7?并完整说明的长度为何在此时等于7的理由.
(2)承(1)小题,请判断当不是你指出的角度时,的长度小于7还是大于7?并完整说明你判断的理由.
【答案】(1)时,.证明见解析
(2)的长度小于7,理由见解析
【分析】本题考查轴对称的性质、三角形的三边关系,(1)连接、,根据轴对称的性质可得,,然后判断出点P、B、R三点共线时,再根据平角的定义求解;(2)根据三角形的任意两边之和大于第三边解答.
【详解】(1)解:如图,时,,证明如下:
连接、,
∵P、R为O分别以直线、为对称轴的对称点,
∴,,
∵,
,
∴点P、B、R三点共线,
∴;
(2)解:的长度小于7,理由如下:
当,则点P、B、R三点不在同一直线上,
∴,
∵,
∴,
即的长度小于7.
【变式4-3】(23-24八年级·山东聊城·期中)如图,直线,相交于点,为这两条直线外一点,连接.点关于直线,的对称点分别是点,.若,则点,之间的距离可能是( )
A.0 B.5 C.7 D.9
【答案】B
【分析】本题考查了轴对称的性质、三角形的三边关系,熟练掌握轴对称的性质是解题关键.连接,先根据轴对称的性质可得,再根据三角形的三边关系定理求解即可得.
【详解】解:如图,连接,
∵点关于直线,的对称点分别是点,,且,
,
在中,,
,
故选:B.
【题型5 折叠问题】
【例5】(23-24八年级·北京·期末)一张正方形纸片经过两次对折,并在如图所示的位置上剪去一个小正方形,打开后的图形是( )
A.B. C.D.
【答案】A
【分析】由平面图形的折叠及图形的对称性展开图解题.
【详解】由第一次对折后中间有一个矩形,排除B、C;
由第二次折叠矩形正在折痕上,排除D;
故选:A.
【点睛】本题考查的是学生的立体思维能力及动手操作能力,关键是由平面图形的折叠及图形的对称性展开图解答.
【变式5-1】(23-24八年级·浙江温州·期末)如图,点为长方形纸片的边上一点,将长方形纸片分别沿,折叠,使点,分别与点,重合,点,,恰好在同一条直线上.若,则的度数为( )
A. B. C. D.
【答案】C
【分析】本题考查了折叠的性质、几何图中角度的计算,由折叠的性质可得,,求出,结合得出,,即可得解,熟练掌握折叠的性质是解此题的关键.
【详解】解:由折叠的性质可得:,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
故选:C.
【变式5-2】(23-24八年级·云南昆明·开学考试)一个长8厘米,宽5厘米的长方形纸片,沿对角线对折后,得到下面所示几何图形,阴影部分的周长是 厘米.
【答案】
【分析】本题是考查简单图形的折叠问题,动手操作一下即可看出阴影部分的周长是长方形的周长,再根据长方形周长公式求解,即可解题.
【详解】解:如图:
由折叠的特点可知,,,
阴影部分的周长是:(厘米),
故答案为:.
【变式5-3】(23-24八年级·陕西西安·期末)将如图(1)所示的长方形纸片按如下步骤操作:(1)如图(2),以过点A的直线为对称轴折叠纸片,使点B恰好落在边上的点处,折痕与交于点E;(2)如图(3),以过点E的直线为对称轴折叠纸片,使点A恰好落在边上的点处,折痕交边于点F;(3)将纸片展平.那么的度数为 .
【答案】
【分析】根据折叠的性质,可知,.由第一次折叠后,由第二次折叠,即可求解.
【详解】解:如图所示,将纸片展平后,根据折叠的性质,可知,.
∴第一次折叠后.
∵纸片为长方形,
∴.
∴.
∴.
∴第二次折叠后.
∴将纸片展平后, .
故答案为:.
【点睛】本题考查了矩形的性质、折叠的性质以及平行线的性质等知识,熟练掌握矩形的性质和折叠的性质是解题的关键.
【题型6 镜面对称】
【例6】(23-24八年级·贵州遵义·期末)如图是一只停放在平静水面上的小船,则它在水中的倒影表示正确的是( )
A. B.
C. D.
【答案】A
【分析】根据镜面对称的性质求解,在平面镜中的像与现实中的事物恰好左右或上下顺序颠倒,且关于镜面对称.
【详解】解:这两个图应关于水面对称,旗子的方向应该朝左,船头应该向左.A选项符合题意;
故选:A.
【点睛】此题主要考查了镜面对称的性质,解决本题的关键是根据所给图形的特征利用轴对称得到相应图形.
【变式6-1】(23-24八年级·河南许昌·期中)小明照镜子的时候,发现T恤上的英文单词 APPLE在镜子中呈现的样子( )
A. B. C. D.
【答案】A
【分析】根据镜面对称的性质,在平面镜中的像与现实中的事物恰好左右颠倒,且关于镜面对称,分析并作答.
【详解】解:根据镜面对称的性质,分析可得题中所给的图片与A显示的图片成轴对称,
故选A.
【点睛】本题考查镜面反射的原理与性质.解决此类题应认真观察,注意技巧.
【变式6-2】(23-24八年级·内蒙古呼和浩特·期中)小明在镜中看到身后墙上的时钟如下,你认为实际时间最接近9:00( )
A.B.C.D.
【答案】B
【分析】根据镜面对称的性质,在平面镜中的钟面上的时针、分针的位置和实物应关于过12时、6时的直线成轴对称.
【详解】9点的时钟,在镜子里看起来应该是3点,所以最接近9点的时间在镜子里看起来就更接近3点,所以应该是图B所示,最接近9点时间.
故选:B.
【点睛】主要考查镜面对称的性质:在平面镜中的像与现实中的事物恰好左右或上下顺序颠倒,且关于镜面对称.
【变式6-3】(23-24八年级·福建龙岩·阶段练习)在平面镜里看到背后墙上的电子钟示数如图所示,这时的实际时间应是 .
【答案】
【分析】本题考查镜面反射的原理与性质.根据镜面对称的性质求解,在平面镜中的像与现实中的事物恰好左右或上下顺序颠倒,且关于镜面对称.
【详解】根据镜面对称的性质,题中所显示的时刻与成轴对称,所以此时实际时刻为:.
故答案为:.
【题型7 画轴对称图形】
【例7】(23-24八年级·山东枣庄·期末)如图,的三个顶点分别位于正方形网格线的交点上,我们把称为格点三角形,请你分别在图①,图②,图③的正方形网格中作一个格点三角形与成轴对称(所作图形不能重复),并画出对称轴.
【答案】见解析(画出三个即可)
【分析】本题主要考查的是画轴对称图形,属于基础题型.首先画出对称轴,然后根据轴对称图形的性质画出图形即可.
【详解】解:如图,即为所求作的三角形.
【变式7-1】(23-24八年级·陕西西安·期末)如图,方格纸中每个小正方形的边长均为,的顶点都在小正方形的顶点上,
(1)在图中画出,使与关于所在直线对称,点与点是对称点;
(2)求四边形的面积.
【答案】(1)见解析
(2)
【分析】本题考查了作图——轴对称变换,解题的关键是掌握轴对称的性质.
(1)根据轴对称的性质作图即可;
(2)根据,即可求解.
【详解】(1)解:如图,即为所求;
(2)解:.
【变式7-2】(23-24八年级·山东济南·期末)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.已知的顶点均在格点上.
(1)画出格点三角形关于直线对称的;
(2)的面积是
(3)在直线上找出点P,使最大,并求出最大值为 .(保留作图痕迹)
【答案】(1)见解析
(2)
(3)见解析,
【分析】本题考查作图-轴对称变换,线段最短,勾股定理;
(1)根据轴对称的性质作图即可.
(2)利用割补法求三角形的面积即可.
(3)延长,交直线于点,则点即为所求.利用勾股定理求出的长,即可得出答案.
【详解】(1)解:如图所示,即为所求;
(2)的面积是
(3)如图所示,延长,交直线于点,
此时,为最大值,
则点即为所求.
由勾股定理得,,
最大值为.
故答案为:.
【变式7-3】(23-24八年级·全国·假期作业)如图1,在的网格中,三个顶点均在格点上,这样的三角形叫做“格点三角形”.在图中画出一个“格点三角形”(阴影部分)与原关于某条直线成轴对称.请在图2、图3、图4中,各画一个和原三角形成轴对称的“格点三角形”,并将所画的“格点三角形”用“斜线”涂成“阴影部分”(图图4不重复).
【答案】见解析
【分析】本题考查了作图轴对称变换:先确定图形的关键点;再利用轴对称性质作出关键点的对称点;然后按原图形中的方式顺次连接对称点.根据轴对称的性质画图.
【详解】解:如图,
【题型8 台球桌上的轴对称】
【例8】(23-24八年级·山东德州·期中)如图,桌球的桌面上有M,N两个球,若要将M球射向桌面的一边,反弹一次后击中N球,则A,B,C,D,4个点中,可以反弹击中N球的是 点.
【答案】D
【分析】本题考查了轴对称的知识,注意结合图形解答,不要凭空想象,实际操作一下.
【详解】解:如图,
可以瞄准点击球.
故答案为:.
【变式8-1】(23-24八年级·江苏苏州·阶段练习)如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是 ( )
A.点A B.点B C.点C D.点D
【答案】D
【分析】如下图
【详解】如图,
由图可知可以瞄准的点为点D.故选D.
【变式8-2】(23-24八年级·全国·课堂例题)如图所示,长方形是台球台面,有白、黑两球分别位于点M,N处,试问:怎样撞击白球M,才能使白球M碰撞台边反弹后击中黑球N?
【答案】见解析
【分析】本题是日常生活中常见的台球问题,通过感知并描述台球的运动规律,想象出小球被撞击后的运动路线,可利用轴对称的性质作出图形,培养了空间观念和应用意识.要使白球M碰撞台边反弹后击中黑球N,可画点M关于的对称点,连接交于点O,则沿方向撞击白球可满足要求.
【详解】解:如图所示,画点M关于的对称点;连接交于点O,则白球M沿碰撞台边,必沿反弹击中黑球N.
理由:由轴对称性质得.
又∵,
∴.
∴白球M沿碰撞台边,必沿反弹击中黑球N.
【变式8-3】(23-24八年级·江苏常州·期中)如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到矩形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到矩形的边时的点为Q,第2次碰到矩形的边时的点为M,….第2022次碰到矩形的边时的点为图中的( )
A.点P B.点Q C.点M D.点N
【答案】A
【分析】根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2022除以6,根据商和余数的情况确定所对应的点的坐标即可.
【详解】解:如图,经过6次反弹后动点回到出发点P,
∵2022÷6=337,
∴当点P第2022次碰到矩形的边时为第337个循环组的最后一次反弹,
∴第2022次碰到矩形的边时的点为图中的点P,
故选:A.
【点睛】此题主要考查了点的坐标的规律,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
【题型9 添加图形使成为轴对称图形】
【例9】(2024·河北石家庄·模拟预测)如图所示的方格纸,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个被涂黑的图案构成一个轴对称图形,那么涂法共有( )种.
A.6 B.5 C.4 D.3
【答案】A
【分析】根据轴对称的概念作答,如果一个图形沿一条直线对折,直线两旁的部分能互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴进行分析,得出共有6处满足题意.
【详解】选择一个正方形涂黑,使得3个涂黑的正方形组成轴对称图形,
选择的位置有以下几种:1处,2处,3处,4处,5处,6处,选择的位置共有6处.
故选:A.
【点睛】本题考查了轴对称图形的定义,根据定义构建轴对称图形,成为轴对称图形每种可能性都必须考虑到,不能有遗漏.
【变式9-1】(23-24八年级·河南安阳·期末)(1)如图,在由小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑2个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰为轴对称图形.请在下图中画出两种不同的填涂方案设计,并用虚线标出对称轴;
【答案】见解析.
【分析】直接利用轴对称图形的性质分别作出符合题意的图形即可;
【详解】解:如图所示:
【点睛】此题主要考查了利用轴对称设计图案,正确掌握轴对称图形的性质是解题关键.
【变式9-2】(23-24八年级·山东聊城·期中)乐乐觉得轴对称图形很有意思,如图是4个完全相同的小正方形组成的形图,请你用三种方法分别在图中添画一个小正方形,使添画后的图形成为轴对称图形.
【答案】见解析
【分析】根据轴对称图形的定义添加即可.
【详解】解: 如图.
【点睛】此题考查轴对称图形的定义,掌握轴对称图形的特点是解题的关键.
【变式9-3】(23-24八年级·江苏无锡·期中)在4×4的方格中有五个同样大小的正方形如图摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有 种.
【答案】13
【分析】根据轴对称图形的性质,分别移动一个正方形,即可得出符合要求的答案.
【详解】如图所示:
一共有13画法,
故答案为:13
【题型10 设计轴对称图案】
【例10】(23-24八年级·河北保定·期中)如图,是由4×4个大小完在一样的小正方形组成的方格纸,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)
【答案】见解析.
【分析】直接利用轴对称图形的性质分别得出符合题意的答案.
【详解】解:如图所示:
【点睛】此题主要考查了利用轴对称设计图案,正确掌握轴对称图形的性质是解题关键.
【变式10-1】(23-24八年级·江苏扬州·期末)如图1是3×3的正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,(要求:绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图2中的两幅图就视为同一种图案),请在图3中的四幅图中完成你的设计.
【答案】见解析
【分析】根据轴对称的性质画出图形即可.
【详解】解:如图所示.
【点睛】本题考查的是利用轴对称设计图案,熟知轴对称的性质是解答此题的关键.
【变式10-2】(23-24八年级·甘肃平凉·期末)如图所示,
(1)观察图①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征:
(2)借助图⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所给出的两个共同特征.(注意:新图案与图①~④的图案不能重合)
【答案】(1)一、都是轴对称图形;二、阴影部分面积都等于四个小正方形的面积之和
(2)见详解
【分析】本题主要考查从不同图形中寻找共同特征的能力,考查观察能力、抽象概括能力、数学语言表述能力和空间观念;
(1)可以从图形的对称性和图形阴影部分的面积来考虑;
(2)根据两个特征设计出一个图案即可;
【详解】(1)所给的四个图案具有的共同特征:一都是轴对称图形;二,阴影部分面积都等于四个小正方形的面积之和;
(2)同时具备上述两个特征的部分图案如下:
【变式10-3】(2024·山东枣庄·中考真题)(1)观察分析:在一次数学综合实践活动中,老师向同学们展示了图①,图②,图③三幅图形,请你结合自己所学的知识,观察图中阴影部分构成的图案,写出三个图案都具有的两个共同特征:___________,___________.
(2)动手操作:请在图④中设计一个新的图案,使其满足你在(1)中发现的共同特征.
【答案】(1)观察发现四个图形都是轴对称图形,且面积相等;(2)见解析
【分析】(1)应从对称方面,阴影部分的面积等方面入手思考;
(2)应画出既是轴对称图形,且面积为4的图形.
【详解】解:(1)观察发现四个图形都是轴对称图形,且面积相等;
故答案为:观察发现四个图形都是轴对称图形,且面积相等;
(2)如图:
【点睛】此题主要考查了利用轴对称图形设计图案,关键是掌握利用轴对称的作图方法来作图,通过变换对称轴来得到不同的图案.
21世纪教育网(www.21cnjy.com)
【人教版】
【题型1 识别轴对称图形】 1
【题型2 确定对称轴的条数】 2
【题型3 由轴对称图形的特征进行判断】 3
【题型4 由轴对称图形的特征进行求解】 4
【题型5 折叠问题】 5
【题型6 镜面对称】 6
【题型7 画轴对称图形】 7
【题型8 台球桌上的轴对称】 8
【题型9 添加图形使成为轴对称图形】 10
【题型10 设计轴对称图案】 11
知识点1:轴对称
(1)轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴
对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称.
(2)轴对称图形是针对一个图形而言的,是一种具有特殊性质图形,被一条直线分割成的两部分沿着对称
轴折叠时,互相重合;轴对称图形的对称轴可以是一条,也可以是多条甚至无数条.
【题型1 识别轴对称图形】
【例1】(23-24八年级·黑龙江哈尔滨·阶段练习)下列图形中,不是轴对称图形的是( ).
A. B. C. D.
【变式1-1】(23-24八年级·广东广州·期末)下列图形中,是轴对称图形的是( )
A.平行四边形 B.直角梯形 C.正五边形 D.直角三角形
【变式1-2】(23-24八年级·吉林四平·期末)下列三角形中,不是轴对称图形的是( )
A.有两个角相等的三角形
B.有两个角分别是120°和30°的三角形
C.有一个角是45°的直角三角形
D.有一个角是60°的直角三角形
【变式1-3】(23-24八年级·重庆南岸·期末)图是的正方形网格,每个小正方形的顶点称为格点.其中点均在格点上.请在给定的网格中,找一格点,使以点为顶点的四边形是轴对称图形,满足条件的点的个数是 个.
知识点2:轴对称的性质
(1)如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
由轴对称的性质得到一下结论:
①如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称;
②如果两个图形成轴对称,我们只要找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这
两个图形的对称轴.
(2)轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
【题型2 确定对称轴的条数】
【例2】(23-24八年级·江苏宿迁·期末)在等腰直角三角形、等边三角形、半圆、正方形这四种常见的轴对称图形中,对称轴最多的是 .
【变式2-1】(23-24八年级·山东烟台·期末)下列图形中是轴对称图形,且对称轴只有两条的是( )
A. B. C. D.
【变式2-2】(23-24八年级·黑龙江大庆·期中)要使大小两个圆组合成的图形有无数条对称轴,应采用第( )种画法
A. B. C. D.
【变式2-3】(23-24八年级·河北廊坊·期末)如图,在由小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑n个小正三角形,使它们和原来涂黑的小正三角形组成的新图案恰有三条对称轴,则n的最小值为( )
A.1 B.2 C.3 D.6
【题型3 由轴对称图形的特征进行判断】
【例3】(23-24八年级·全国·课后作业)如图,正六边形关于直线l成轴对称的图形是正六边形,有下列说法:①;②;③直线;④.其中正确的是 (请写出所有正确说法的序号).
【变式3-1】(23-24八年级·全国·课后作业)下列说法正确的是( )
A.任何一个图形都有对称轴
B.两个全等三角形一定关于某直线对称
C.若与成轴对称,则
D.点,点在直线两旁,且与直线交于点,若,则点与点关于直线对称
【变式3-2】(23-24八年级·全国·假期作业)如图,与关于直线对称,为上任一点(,,不共线),下列结论中不正确的是( )
A. B.垂直平分线段
C.与面积相等 D.直线,的交点不一定在直线上
【变式3-3】(23-24八年级·全国·课后作业)一个图形沿一条直线翻折后再沿这条直线的方向平移,我们把这样的图形运动称为图形的翻移,这条直线称为翻移线.如图△A2B2C2是由△ABC沿直线l翻移后得到的.在下列结论中,图形的翻移所具有的性质是( )
A.各对应点之间的距离相等 B.各对应点的连线互相平行
C.对应点连线被翻移线平分 D.对应点连线与翻移线垂直
【题型4 由轴对称图形的特征进行求解】
【例4】(23-24八年级·辽宁沈阳·期末)如图,AD所在直线是△ABC的对称轴,点E,F是AD上的两点,若BD=3,AD=5,则图中阴影部分的面积是 .
【变式4-1】(23-24八年级·浙江杭州·开学考试)如图所示的2×2方格中,连接AB,AC,AD,则∠A+∠B+∠C的和( ).
A.必是直角 B.必是锐角 C.必是钝角 D.是锐角或钝角
【变式4-2】(23-24八年级·全国·假期作业)如图,O为内部一点,,P、R为O分别以直线、为对称轴的对称点.
(1)请指出当是什么角度时,会使得的长度等于7?并完整说明的长度为何在此时等于7的理由.
(2)承(1)小题,请判断当不是你指出的角度时,的长度小于7还是大于7?并完整说明你判断的理由.
【变式4-3】(23-24八年级·山东聊城·期中)如图,直线,相交于点,为这两条直线外一点,连接.点关于直线,的对称点分别是点,.若,则点,之间的距离可能是( )
A.0 B.5 C.7 D.9
【题型5 折叠问题】
【例5】(23-24八年级·北京·期末)一张正方形纸片经过两次对折,并在如图所示的位置上剪去一个小正方形,打开后的图形是( )
A.B. C.D.
【变式5-1】(23-24八年级·浙江温州·期末)如图,点为长方形纸片的边上一点,将长方形纸片分别沿,折叠,使点,分别与点,重合,点,,恰好在同一条直线上.若,则的度数为( )
A. B. C. D.
【变式5-2】(23-24八年级·云南昆明·开学考试)一个长8厘米,宽5厘米的长方形纸片,沿对角线对折后,得到下面所示几何图形,阴影部分的周长是 厘米.
【变式5-3】(23-24八年级·陕西西安·期末)将如图(1)所示的长方形纸片按如下步骤操作:(1)如图(2),以过点A的直线为对称轴折叠纸片,使点B恰好落在边上的点处,折痕与交于点E;(2)如图(3),以过点E的直线为对称轴折叠纸片,使点A恰好落在边上的点处,折痕交边于点F;(3)将纸片展平.那么的度数为 .
【题型6 镜面对称】
【例6】(23-24八年级·贵州遵义·期末)如图是一只停放在平静水面上的小船,则它在水中的倒影表示正确的是( )
A. B.
C. D.
【变式6-1】(23-24八年级·河南许昌·期中)小明照镜子的时候,发现T恤上的英文单词 APPLE在镜子中呈现的样子( )
A. B. C. D.
【变式6-2】(23-24八年级·内蒙古呼和浩特·期中)小明在镜中看到身后墙上的时钟如下,你认为实际时间最接近9:00( )
A.B.C.D.
【变式6-3】(23-24八年级·福建龙岩·阶段练习)在平面镜里看到背后墙上的电子钟示数如图所示,这时的实际时间应是 .
【题型7 画轴对称图形】
【例7】(23-24八年级·山东枣庄·期末)如图,的三个顶点分别位于正方形网格线的交点上,我们把称为格点三角形,请你分别在图①,图②,图③的正方形网格中作一个格点三角形与成轴对称(所作图形不能重复),并画出对称轴.
【变式7-1】(23-24八年级·陕西西安·期末)如图,方格纸中每个小正方形的边长均为,的顶点都在小正方形的顶点上,
(1)在图中画出,使与关于所在直线对称,点与点是对称点;
(2)求四边形的面积.
【变式7-2】(23-24八年级·山东济南·期末)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.已知的顶点均在格点上.
(1)画出格点三角形关于直线对称的;
(2)的面积是
(3)在直线上找出点P,使最大,并求出最大值为 .(保留作图痕迹)
【变式7-3】(23-24八年级·全国·假期作业)如图1,在的网格中,三个顶点均在格点上,这样的三角形叫做“格点三角形”.在图中画出一个“格点三角形”(阴影部分)与原关于某条直线成轴对称.请在图2、图3、图4中,各画一个和原三角形成轴对称的“格点三角形”,并将所画的“格点三角形”用“斜线”涂成“阴影部分”(图图4不重复).
【题型8 台球桌上的轴对称】
【例8】(23-24八年级·山东德州·期中)如图,桌球的桌面上有M,N两个球,若要将M球射向桌面的一边,反弹一次后击中N球,则A,B,C,D,4个点中,可以反弹击中N球的是 点.
【变式8-1】(23-24八年级·江苏苏州·阶段练习)如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是 ( )
A.点A B.点B C.点C D.点D
【变式8-2】(23-24八年级·全国·课堂例题)如图所示,长方形是台球台面,有白、黑两球分别位于点M,N处,试问:怎样撞击白球M,才能使白球M碰撞台边反弹后击中黑球N?
【变式8-3】(23-24八年级·江苏常州·期中)如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到矩形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到矩形的边时的点为Q,第2次碰到矩形的边时的点为M,….第2022次碰到矩形的边时的点为图中的( )
A.点P B.点Q C.点M D.点N
【题型9 添加图形使成为轴对称图形】
【例9】(2024·河北石家庄·模拟预测)如图所示的方格纸,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个被涂黑的图案构成一个轴对称图形,那么涂法共有( )种.
A.6 B.5 C.4 D.3
【变式9-1】(23-24八年级·河南安阳·期末)(1)如图,在由小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑2个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰为轴对称图形.请在下图中画出两种不同的填涂方案设计,并用虚线标出对称轴;
【变式9-2】(23-24八年级·山东聊城·期中)乐乐觉得轴对称图形很有意思,如图是4个完全相同的小正方形组成的形图,请你用三种方法分别在图中添画一个小正方形,使添画后的图形成为轴对称图形.
【变式9-3】(23-24八年级·江苏无锡·期中)在4×4的方格中有五个同样大小的正方形如图摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有 种.
【题型10 设计轴对称图案】
【例10】(23-24八年级·河北保定·期中)如图,是由4×4个大小完在一样的小正方形组成的方格纸,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)
【变式10-1】(23-24八年级·江苏扬州·期末)如图1是3×3的正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,(要求:绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图2中的两幅图就视为同一种图案),请在图3中的四幅图中完成你的设计.
【变式10-2】(23-24八年级·甘肃平凉·期末)如图所示,
(1)观察图①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征:
(2)借助图⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所给出的两个共同特征.(注意:新图案与图①~④的图案不能重合)
【变式10-3】(2024·山东枣庄·中考真题)(1)观察分析:在一次数学综合实践活动中,老师向同学们展示了图①,图②,图③三幅图形,请你结合自己所学的知识,观察图中阴影部分构成的图案,写出三个图案都具有的两个共同特征:___________,___________.
(2)动手操作:请在图④中设计一个新的图案,使其满足你在(1)中发现的共同特征.
21世纪教育网(www.21cnjy.com)
专题13.1 轴对称【十大题型】
【人教版】
【题型1 识别轴对称图形】 1
【题型2 确定对称轴的条数】 3
【题型3 由轴对称图形的特征进行判断】 5
【题型4 由轴对称图形的特征进行求解】 8
【题型5 折叠问题】 11
【题型6 镜面对称】 14
【题型7 画轴对称图形】 16
【题型8 台球桌上的轴对称】 19
【题型9 添加图形使成为轴对称图形】 22
【题型10 设计轴对称图案】 24
知识点1:轴对称
(1)轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴
对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称.
(2)轴对称图形是针对一个图形而言的,是一种具有特殊性质图形,被一条直线分割成的两部分沿着对称
轴折叠时,互相重合;轴对称图形的对称轴可以是一条,也可以是多条甚至无数条.
【题型1 识别轴对称图形】
【例1】(23-24八年级·黑龙江哈尔滨·阶段练习)下列图形中,不是轴对称图形的是( ).
A. B. C. D.
【答案】B
【分析】根据轴对称图形的定义,一个图形沿着一条直线折叠,直线两旁的部分能够相互重合,那么这个图形叫做轴对称图形,对选项进行分析判断即可.
【详解】解:选项、、中的图形都能找到对称轴,使得对称轴两旁的部分能够相互重合,都是轴对称图形,选项中的图形,没有对称轴可以使对称轴两旁的部分能够相互重合,不是轴对称图形,
故选:.
【点睛】本题考查轴对称图形,解答本题的关键是明确轴对称图形的定义,一个图形沿着一条直线折叠,直线两旁的部分能够相互重合,那么这个图形叫做轴对称图形.
【变式1-1】(23-24八年级·广东广州·期末)下列图形中,是轴对称图形的是( )
A.平行四边形 B.直角梯形 C.正五边形 D.直角三角形
【答案】C
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
【详解】解:A、平行四边形不是轴对称图形,故本选项不合题意;
B、直角梯形不是轴对称图形,故本选项不合题意;
C、正五边形是轴对称图形,故本选项符合题意;
D、直角三角形不是轴对称图形,故本选项不合题意.
故选:C.
【点睛】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
【变式1-2】(23-24八年级·吉林四平·期末)下列三角形中,不是轴对称图形的是( )
A.有两个角相等的三角形
B.有两个角分别是120°和30°的三角形
C.有一个角是45°的直角三角形
D.有一个角是60°的直角三角形
【答案】D
【分析】根据轴对称图形的概念求解.直角三角形中只有等腰直角三角形是轴对称图形.
如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
【详解】解:根据轴对称图形的定义:
A、有两个内角相等的三角形,是轴对称图形,不符合题意;
B、有两个角分别是120°和30°的三角形,另一个内角也是30°,故是轴对称图形,不符合题意;
C、有一个内角为45°的直角三角形,是轴对称图形,不符合题意
D、有一个角是60°的直角三角形,找不到对称轴,则不是轴对称图形,符合题意.
故选D.
【点睛】本题考查轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
【变式1-3】(23-24八年级·重庆南岸·期末)图是的正方形网格,每个小正方形的顶点称为格点.其中点均在格点上.请在给定的网格中,找一格点,使以点为顶点的四边形是轴对称图形,满足条件的点的个数是 个.
【答案】2
【分析】根据轴对称图形的定义,动手逐个判断即可求解.
【详解】解:如图所示,
即:满足条件的点的个数为2个,
故答案为:2.
【点睛】本题主要考查了轴对称图形,熟练掌握轴对称图形的定义:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形是解题的关键.
知识点2:轴对称的性质
(1)如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
由轴对称的性质得到一下结论:
①如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称;
②如果两个图形成轴对称,我们只要找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这
两个图形的对称轴.
(2)轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
【题型2 确定对称轴的条数】
【例2】(23-24八年级·江苏宿迁·期末)在等腰直角三角形、等边三角形、半圆、正方形这四种常见的轴对称图形中,对称轴最多的是 .
【答案】正方形
【分析】本题考查了求对称轴条数,分别写出各个图形的对称轴的条数,比较即可得出答案.
【详解】解:等腰直角三角形有条对称轴;
等边三角形有条对称轴;
半圆由条对称轴;
正方形有条对称轴;
∴对称轴最多的是正方形,
故答案为:正方形.
【变式2-1】(23-24八年级·山东烟台·期末)下列图形中是轴对称图形,且对称轴只有两条的是( )
A. B. C. D.
【答案】A
【分析】本题考查了轴对称图形的识别,解题的关键是掌握一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形是轴对称图形,这条直线是对称轴.
【详解】解:A、是轴对称图形,有2条对称轴,符合题意;
B、是轴对称图形,有1条对称轴,不符合题意;
C、不是轴对称图形,不符合题意;
D、是轴对称图形,有8条对称轴,不符合题意;
故选:A.
【变式2-2】(23-24八年级·黑龙江大庆·期中)要使大小两个圆组合成的图形有无数条对称轴,应采用第( )种画法
A. B. C. D.
【答案】B
【分析】此题考查轴对称图形定义及对称轴的条数,一个图形沿某条直线对折,直线两旁的部分能够完全重合,这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴.
【详解】解:在给出的选项中的图形中,A ,C ,D有1条对称轴,B 有无数条对称轴.
所以要使大小两个圆有无数条对称轴,应采用B画法.
故选:B.
【变式2-3】(23-24八年级·河北廊坊·期末)如图,在由小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑n个小正三角形,使它们和原来涂黑的小正三角形组成的新图案恰有三条对称轴,则n的最小值为( )
A.1 B.2 C.3 D.6
【答案】C
【分析】本题考查了利用轴对称设计图案,解题的关键是掌握常见图形的性质和轴对称图形的性质.由等边三角形有三条对称轴可得答案.
【详解】解:如图所示,n的最小值为3.
故选:C.
【题型3 由轴对称图形的特征进行判断】
【例3】(23-24八年级·全国·课后作业)如图,正六边形关于直线l成轴对称的图形是正六边形,有下列说法:①;②;③直线;④.其中正确的是 (请写出所有正确说法的序号).
【答案】①③④
【分析】根据轴对称的性质,多边形的内角和求解,然后判断作答即可.
【详解】解:由轴对称的性质可得,,直线,,
∴①③④正确,故符合要求;②错误,故不符合要求;
故答案为:①③④.
【点睛】本题考查了轴对称的性质,多边形的内角和.解题的关键在于对知识的熟练掌握与灵活运用.
【变式3-1】(23-24八年级·全国·课后作业)下列说法正确的是( )
A.任何一个图形都有对称轴
B.两个全等三角形一定关于某直线对称
C.若与成轴对称,则
D.点,点在直线两旁,且与直线交于点,若,则点与点关于直线对称
【答案】C
【分析】根据轴对称的定义:两个图形沿一条直线对着,直线两旁的部分能完全重合,那么这两个图形成轴对称进行判断即可.
【详解】A.有的图形没有对称轴,该选项错误;
B.由于位置关系不明确,如图一,该选项错误,
C. 若与成轴对称,则,该选项正确;
D、因为线段与直线不一定垂直,所以不能正确判定,该选项错误.
故选:C.
【点睛】本题主要考查了轴对称图形,关键是熟练把握轴对称的定义.
【变式3-2】(23-24八年级·全国·假期作业)如图,与关于直线对称,为上任一点(,,不共线),下列结论中不正确的是( )
A. B.垂直平分线段
C.与面积相等 D.直线,的交点不一定在直线上
【答案】D
【分析】利用轴对称的性质解答.
【详解】解:与关于直线对称,为上任意一点,
垂直平分,
∴,与面积相等,故,,选项不符合题意;
直线,关于直线对称,因此交点一定在上,故D选项符合题意,
故选:D.
【点睛】此题考查轴对称的性质:轴对称图形的对应角相等,对应边相等,轴对称的三角形全等由此面积相等.
【变式3-3】(23-24八年级·全国·课后作业)一个图形沿一条直线翻折后再沿这条直线的方向平移,我们把这样的图形运动称为图形的翻移,这条直线称为翻移线.如图△A2B2C2是由△ABC沿直线l翻移后得到的.在下列结论中,图形的翻移所具有的性质是( )
A.各对应点之间的距离相等 B.各对应点的连线互相平行
C.对应点连线被翻移线平分 D.对应点连线与翻移线垂直
【答案】C
【分析】根据图象的翻折和平移的性质得出对应点连线被翻移线平分.
【详解】∵如图所示:△A2B2C2是由△ABC沿直线l翻移后得到的,
∴图形的翻移所具有的性质是:对应点连线被翻移线平分.
故选C.
【点睛】此题主要考查了几何变换的类型,根据翻折和平移的性质得出是解题关键.
【题型4 由轴对称图形的特征进行求解】
【例4】(23-24八年级·辽宁沈阳·期末)如图,AD所在直线是△ABC的对称轴,点E,F是AD上的两点,若BD=3,AD=5,则图中阴影部分的面积是 .
【答案】
【分析】根据△CEF和△BEF关于直线AD对称,得出S△BEF=S△CEF,根据图中阴影部分的面积是S△ABC求出即可.
【详解】解:∵△ABC关于直线AD对称,
∴B、C关于直线AD对称,
∴△CEF和△BEF关于直线AD对称,
∴S△BEF=S△CEF,
∵△ABC的面积是:×BC×AD=×6×5=15,
∴图中阴影部分的面积是S△ABC=.
故答案为:.
【点睛】本题考查了轴对称的性质.通过观察可以发现是轴对称图形,且阴影部分的面积为全面积的一半,根据轴对称图形的性质求解.其中看出三角形BEF与三角形CEF关于AD对称,面积相等是解决本题的关键.
【变式4-1】(23-24八年级·浙江杭州·开学考试)如图所示的2×2方格中,连接AB,AC,AD,则∠A+∠B+∠C的和( ).
A.必是直角 B.必是锐角 C.必是钝角 D.是锐角或钝角
【答案】C
【分析】观察图形可知该图形关于线段AC所在的直线对称,从而得到∠1+∠3=90°,∠2=45°,从而求得三个角的和.
【详解】解:∵2×2正方格关于线段AC所在的直线对称,
∴∠1=∠4,
∵∠4+∠3=90°,∠2=45°,
∴∠1+∠2+∠3=90°+45°=135°.
故选:C.
【点睛】本题考查了轴对称的性质,角度的计算,以及角的分类,解题的关键是发现本图关于线段AC所在的直线对称.
【变式4-2】(23-24八年级·全国·假期作业)如图,O为内部一点,,P、R为O分别以直线、为对称轴的对称点.
(1)请指出当是什么角度时,会使得的长度等于7?并完整说明的长度为何在此时等于7的理由.
(2)承(1)小题,请判断当不是你指出的角度时,的长度小于7还是大于7?并完整说明你判断的理由.
【答案】(1)时,.证明见解析
(2)的长度小于7,理由见解析
【分析】本题考查轴对称的性质、三角形的三边关系,(1)连接、,根据轴对称的性质可得,,然后判断出点P、B、R三点共线时,再根据平角的定义求解;(2)根据三角形的任意两边之和大于第三边解答.
【详解】(1)解:如图,时,,证明如下:
连接、,
∵P、R为O分别以直线、为对称轴的对称点,
∴,,
∵,
,
∴点P、B、R三点共线,
∴;
(2)解:的长度小于7,理由如下:
当,则点P、B、R三点不在同一直线上,
∴,
∵,
∴,
即的长度小于7.
【变式4-3】(23-24八年级·山东聊城·期中)如图,直线,相交于点,为这两条直线外一点,连接.点关于直线,的对称点分别是点,.若,则点,之间的距离可能是( )
A.0 B.5 C.7 D.9
【答案】B
【分析】本题考查了轴对称的性质、三角形的三边关系,熟练掌握轴对称的性质是解题关键.连接,先根据轴对称的性质可得,再根据三角形的三边关系定理求解即可得.
【详解】解:如图,连接,
∵点关于直线,的对称点分别是点,,且,
,
在中,,
,
故选:B.
【题型5 折叠问题】
【例5】(23-24八年级·北京·期末)一张正方形纸片经过两次对折,并在如图所示的位置上剪去一个小正方形,打开后的图形是( )
A.B. C.D.
【答案】A
【分析】由平面图形的折叠及图形的对称性展开图解题.
【详解】由第一次对折后中间有一个矩形,排除B、C;
由第二次折叠矩形正在折痕上,排除D;
故选:A.
【点睛】本题考查的是学生的立体思维能力及动手操作能力,关键是由平面图形的折叠及图形的对称性展开图解答.
【变式5-1】(23-24八年级·浙江温州·期末)如图,点为长方形纸片的边上一点,将长方形纸片分别沿,折叠,使点,分别与点,重合,点,,恰好在同一条直线上.若,则的度数为( )
A. B. C. D.
【答案】C
【分析】本题考查了折叠的性质、几何图中角度的计算,由折叠的性质可得,,求出,结合得出,,即可得解,熟练掌握折叠的性质是解此题的关键.
【详解】解:由折叠的性质可得:,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
故选:C.
【变式5-2】(23-24八年级·云南昆明·开学考试)一个长8厘米,宽5厘米的长方形纸片,沿对角线对折后,得到下面所示几何图形,阴影部分的周长是 厘米.
【答案】
【分析】本题是考查简单图形的折叠问题,动手操作一下即可看出阴影部分的周长是长方形的周长,再根据长方形周长公式求解,即可解题.
【详解】解:如图:
由折叠的特点可知,,,
阴影部分的周长是:(厘米),
故答案为:.
【变式5-3】(23-24八年级·陕西西安·期末)将如图(1)所示的长方形纸片按如下步骤操作:(1)如图(2),以过点A的直线为对称轴折叠纸片,使点B恰好落在边上的点处,折痕与交于点E;(2)如图(3),以过点E的直线为对称轴折叠纸片,使点A恰好落在边上的点处,折痕交边于点F;(3)将纸片展平.那么的度数为 .
【答案】
【分析】根据折叠的性质,可知,.由第一次折叠后,由第二次折叠,即可求解.
【详解】解:如图所示,将纸片展平后,根据折叠的性质,可知,.
∴第一次折叠后.
∵纸片为长方形,
∴.
∴.
∴.
∴第二次折叠后.
∴将纸片展平后, .
故答案为:.
【点睛】本题考查了矩形的性质、折叠的性质以及平行线的性质等知识,熟练掌握矩形的性质和折叠的性质是解题的关键.
【题型6 镜面对称】
【例6】(23-24八年级·贵州遵义·期末)如图是一只停放在平静水面上的小船,则它在水中的倒影表示正确的是( )
A. B.
C. D.
【答案】A
【分析】根据镜面对称的性质求解,在平面镜中的像与现实中的事物恰好左右或上下顺序颠倒,且关于镜面对称.
【详解】解:这两个图应关于水面对称,旗子的方向应该朝左,船头应该向左.A选项符合题意;
故选:A.
【点睛】此题主要考查了镜面对称的性质,解决本题的关键是根据所给图形的特征利用轴对称得到相应图形.
【变式6-1】(23-24八年级·河南许昌·期中)小明照镜子的时候,发现T恤上的英文单词 APPLE在镜子中呈现的样子( )
A. B. C. D.
【答案】A
【分析】根据镜面对称的性质,在平面镜中的像与现实中的事物恰好左右颠倒,且关于镜面对称,分析并作答.
【详解】解:根据镜面对称的性质,分析可得题中所给的图片与A显示的图片成轴对称,
故选A.
【点睛】本题考查镜面反射的原理与性质.解决此类题应认真观察,注意技巧.
【变式6-2】(23-24八年级·内蒙古呼和浩特·期中)小明在镜中看到身后墙上的时钟如下,你认为实际时间最接近9:00( )
A.B.C.D.
【答案】B
【分析】根据镜面对称的性质,在平面镜中的钟面上的时针、分针的位置和实物应关于过12时、6时的直线成轴对称.
【详解】9点的时钟,在镜子里看起来应该是3点,所以最接近9点的时间在镜子里看起来就更接近3点,所以应该是图B所示,最接近9点时间.
故选:B.
【点睛】主要考查镜面对称的性质:在平面镜中的像与现实中的事物恰好左右或上下顺序颠倒,且关于镜面对称.
【变式6-3】(23-24八年级·福建龙岩·阶段练习)在平面镜里看到背后墙上的电子钟示数如图所示,这时的实际时间应是 .
【答案】
【分析】本题考查镜面反射的原理与性质.根据镜面对称的性质求解,在平面镜中的像与现实中的事物恰好左右或上下顺序颠倒,且关于镜面对称.
【详解】根据镜面对称的性质,题中所显示的时刻与成轴对称,所以此时实际时刻为:.
故答案为:.
【题型7 画轴对称图形】
【例7】(23-24八年级·山东枣庄·期末)如图,的三个顶点分别位于正方形网格线的交点上,我们把称为格点三角形,请你分别在图①,图②,图③的正方形网格中作一个格点三角形与成轴对称(所作图形不能重复),并画出对称轴.
【答案】见解析(画出三个即可)
【分析】本题主要考查的是画轴对称图形,属于基础题型.首先画出对称轴,然后根据轴对称图形的性质画出图形即可.
【详解】解:如图,即为所求作的三角形.
【变式7-1】(23-24八年级·陕西西安·期末)如图,方格纸中每个小正方形的边长均为,的顶点都在小正方形的顶点上,
(1)在图中画出,使与关于所在直线对称,点与点是对称点;
(2)求四边形的面积.
【答案】(1)见解析
(2)
【分析】本题考查了作图——轴对称变换,解题的关键是掌握轴对称的性质.
(1)根据轴对称的性质作图即可;
(2)根据,即可求解.
【详解】(1)解:如图,即为所求;
(2)解:.
【变式7-2】(23-24八年级·山东济南·期末)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.已知的顶点均在格点上.
(1)画出格点三角形关于直线对称的;
(2)的面积是
(3)在直线上找出点P,使最大,并求出最大值为 .(保留作图痕迹)
【答案】(1)见解析
(2)
(3)见解析,
【分析】本题考查作图-轴对称变换,线段最短,勾股定理;
(1)根据轴对称的性质作图即可.
(2)利用割补法求三角形的面积即可.
(3)延长,交直线于点,则点即为所求.利用勾股定理求出的长,即可得出答案.
【详解】(1)解:如图所示,即为所求;
(2)的面积是
(3)如图所示,延长,交直线于点,
此时,为最大值,
则点即为所求.
由勾股定理得,,
最大值为.
故答案为:.
【变式7-3】(23-24八年级·全国·假期作业)如图1,在的网格中,三个顶点均在格点上,这样的三角形叫做“格点三角形”.在图中画出一个“格点三角形”(阴影部分)与原关于某条直线成轴对称.请在图2、图3、图4中,各画一个和原三角形成轴对称的“格点三角形”,并将所画的“格点三角形”用“斜线”涂成“阴影部分”(图图4不重复).
【答案】见解析
【分析】本题考查了作图轴对称变换:先确定图形的关键点;再利用轴对称性质作出关键点的对称点;然后按原图形中的方式顺次连接对称点.根据轴对称的性质画图.
【详解】解:如图,
【题型8 台球桌上的轴对称】
【例8】(23-24八年级·山东德州·期中)如图,桌球的桌面上有M,N两个球,若要将M球射向桌面的一边,反弹一次后击中N球,则A,B,C,D,4个点中,可以反弹击中N球的是 点.
【答案】D
【分析】本题考查了轴对称的知识,注意结合图形解答,不要凭空想象,实际操作一下.
【详解】解:如图,
可以瞄准点击球.
故答案为:.
【变式8-1】(23-24八年级·江苏苏州·阶段练习)如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是 ( )
A.点A B.点B C.点C D.点D
【答案】D
【分析】如下图
【详解】如图,
由图可知可以瞄准的点为点D.故选D.
【变式8-2】(23-24八年级·全国·课堂例题)如图所示,长方形是台球台面,有白、黑两球分别位于点M,N处,试问:怎样撞击白球M,才能使白球M碰撞台边反弹后击中黑球N?
【答案】见解析
【分析】本题是日常生活中常见的台球问题,通过感知并描述台球的运动规律,想象出小球被撞击后的运动路线,可利用轴对称的性质作出图形,培养了空间观念和应用意识.要使白球M碰撞台边反弹后击中黑球N,可画点M关于的对称点,连接交于点O,则沿方向撞击白球可满足要求.
【详解】解:如图所示,画点M关于的对称点;连接交于点O,则白球M沿碰撞台边,必沿反弹击中黑球N.
理由:由轴对称性质得.
又∵,
∴.
∴白球M沿碰撞台边,必沿反弹击中黑球N.
【变式8-3】(23-24八年级·江苏常州·期中)如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到矩形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到矩形的边时的点为Q,第2次碰到矩形的边时的点为M,….第2022次碰到矩形的边时的点为图中的( )
A.点P B.点Q C.点M D.点N
【答案】A
【分析】根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2022除以6,根据商和余数的情况确定所对应的点的坐标即可.
【详解】解:如图,经过6次反弹后动点回到出发点P,
∵2022÷6=337,
∴当点P第2022次碰到矩形的边时为第337个循环组的最后一次反弹,
∴第2022次碰到矩形的边时的点为图中的点P,
故选:A.
【点睛】此题主要考查了点的坐标的规律,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
【题型9 添加图形使成为轴对称图形】
【例9】(2024·河北石家庄·模拟预测)如图所示的方格纸,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个被涂黑的图案构成一个轴对称图形,那么涂法共有( )种.
A.6 B.5 C.4 D.3
【答案】A
【分析】根据轴对称的概念作答,如果一个图形沿一条直线对折,直线两旁的部分能互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴进行分析,得出共有6处满足题意.
【详解】选择一个正方形涂黑,使得3个涂黑的正方形组成轴对称图形,
选择的位置有以下几种:1处,2处,3处,4处,5处,6处,选择的位置共有6处.
故选:A.
【点睛】本题考查了轴对称图形的定义,根据定义构建轴对称图形,成为轴对称图形每种可能性都必须考虑到,不能有遗漏.
【变式9-1】(23-24八年级·河南安阳·期末)(1)如图,在由小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑2个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰为轴对称图形.请在下图中画出两种不同的填涂方案设计,并用虚线标出对称轴;
【答案】见解析.
【分析】直接利用轴对称图形的性质分别作出符合题意的图形即可;
【详解】解:如图所示:
【点睛】此题主要考查了利用轴对称设计图案,正确掌握轴对称图形的性质是解题关键.
【变式9-2】(23-24八年级·山东聊城·期中)乐乐觉得轴对称图形很有意思,如图是4个完全相同的小正方形组成的形图,请你用三种方法分别在图中添画一个小正方形,使添画后的图形成为轴对称图形.
【答案】见解析
【分析】根据轴对称图形的定义添加即可.
【详解】解: 如图.
【点睛】此题考查轴对称图形的定义,掌握轴对称图形的特点是解题的关键.
【变式9-3】(23-24八年级·江苏无锡·期中)在4×4的方格中有五个同样大小的正方形如图摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有 种.
【答案】13
【分析】根据轴对称图形的性质,分别移动一个正方形,即可得出符合要求的答案.
【详解】如图所示:
一共有13画法,
故答案为:13
【题型10 设计轴对称图案】
【例10】(23-24八年级·河北保定·期中)如图,是由4×4个大小完在一样的小正方形组成的方格纸,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)
【答案】见解析.
【分析】直接利用轴对称图形的性质分别得出符合题意的答案.
【详解】解:如图所示:
【点睛】此题主要考查了利用轴对称设计图案,正确掌握轴对称图形的性质是解题关键.
【变式10-1】(23-24八年级·江苏扬州·期末)如图1是3×3的正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,(要求:绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图2中的两幅图就视为同一种图案),请在图3中的四幅图中完成你的设计.
【答案】见解析
【分析】根据轴对称的性质画出图形即可.
【详解】解:如图所示.
【点睛】本题考查的是利用轴对称设计图案,熟知轴对称的性质是解答此题的关键.
【变式10-2】(23-24八年级·甘肃平凉·期末)如图所示,
(1)观察图①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征:
(2)借助图⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所给出的两个共同特征.(注意:新图案与图①~④的图案不能重合)
【答案】(1)一、都是轴对称图形;二、阴影部分面积都等于四个小正方形的面积之和
(2)见详解
【分析】本题主要考查从不同图形中寻找共同特征的能力,考查观察能力、抽象概括能力、数学语言表述能力和空间观念;
(1)可以从图形的对称性和图形阴影部分的面积来考虑;
(2)根据两个特征设计出一个图案即可;
【详解】(1)所给的四个图案具有的共同特征:一都是轴对称图形;二,阴影部分面积都等于四个小正方形的面积之和;
(2)同时具备上述两个特征的部分图案如下:
【变式10-3】(2024·山东枣庄·中考真题)(1)观察分析:在一次数学综合实践活动中,老师向同学们展示了图①,图②,图③三幅图形,请你结合自己所学的知识,观察图中阴影部分构成的图案,写出三个图案都具有的两个共同特征:___________,___________.
(2)动手操作:请在图④中设计一个新的图案,使其满足你在(1)中发现的共同特征.
【答案】(1)观察发现四个图形都是轴对称图形,且面积相等;(2)见解析
【分析】(1)应从对称方面,阴影部分的面积等方面入手思考;
(2)应画出既是轴对称图形,且面积为4的图形.
【详解】解:(1)观察发现四个图形都是轴对称图形,且面积相等;
故答案为:观察发现四个图形都是轴对称图形,且面积相等;
(2)如图:
【点睛】此题主要考查了利用轴对称图形设计图案,关键是掌握利用轴对称的作图方法来作图,通过变换对称轴来得到不同的图案.
21世纪教育网(www.21cnjy.com)
