初中数学人教版八年级上册11.1.2三角形的高、中线与角平分线 教学课件(共24张PPT)
文档属性
| 名称 | 初中数学人教版八年级上册11.1.2三角形的高、中线与角平分线 教学课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 18.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
11.1.2 三角形的高、中线与角平分线
第十一章——三角形
CONTENTS
了解三角形的高、中线与角平分线的概念;
了解三角形的重心的概念;
能正确画出一个三角形的高、中线、角平分线,并掌握其相关性质.
01
02
03
回顾我们之前所学的垂线、线段中点、角平分线的概念
垂线:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
线段中点:把一条线段分成两条相等的线段的点
角平分线:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
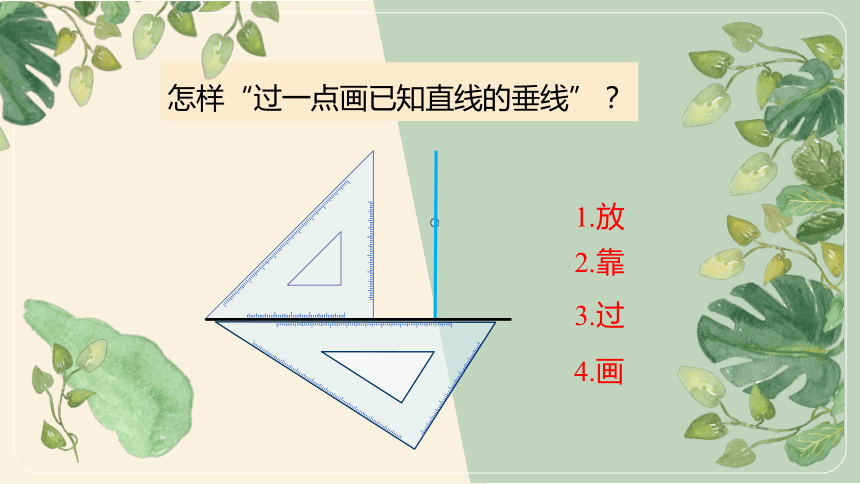
怎样“过一点画已知直线的垂线”?
1.放
2.靠
3.过
4.画
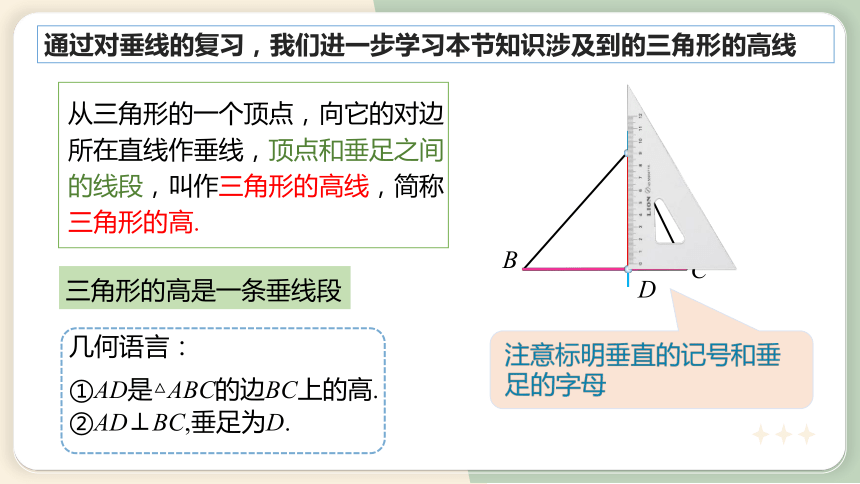
通过对垂线的复习,我们进一步学习本节知识涉及到的三角形的高线
三角形的高是一条垂线段
从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段,叫作三角形的高线,简称三角形的高.
A
B
C
D
注意标明垂直的记号和垂足的字母
几何语言:
①AD是△ABC的边BC上的高.
②AD⊥BC,垂足为D.
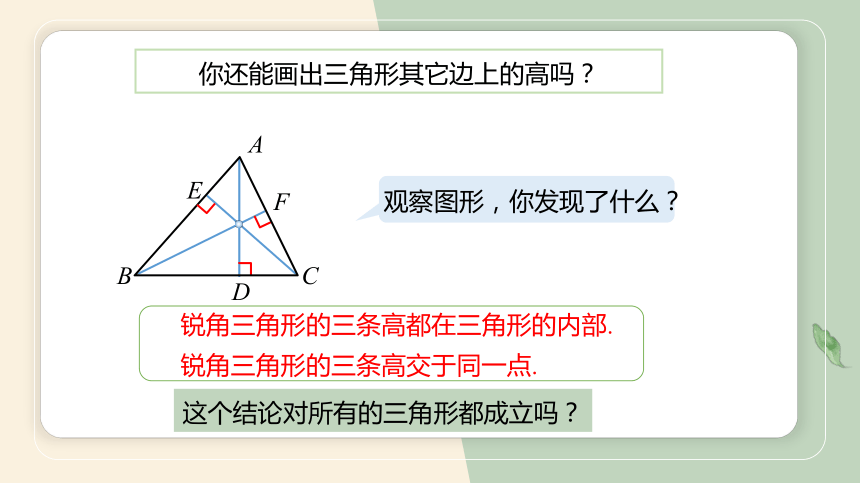
你还能画出三角形其它边上的高吗?
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
观察图形,你发现了什么?
锐角三角形的三条高都在三角形的内部.
这个结论对所有的三角形都成立吗?
A
B
C
D
E
F
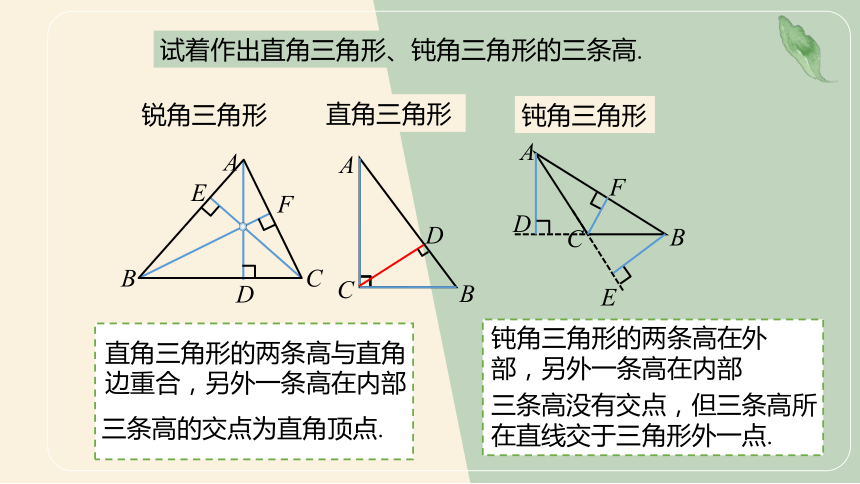
试着作出直角三角形、钝角三角形的三条高.
A
B
C
D
锐角三角形
直角三角形
A
B
C
D
钝角三角形
E
F
直角三角形的两条高与直角边重合,另外一条高在内部
三条高的交点为直角顶点.
钝角三角形的两条高在外部,另外一条高在内部
三条高没有交点,但三条高所在直线交于三角形外一点.
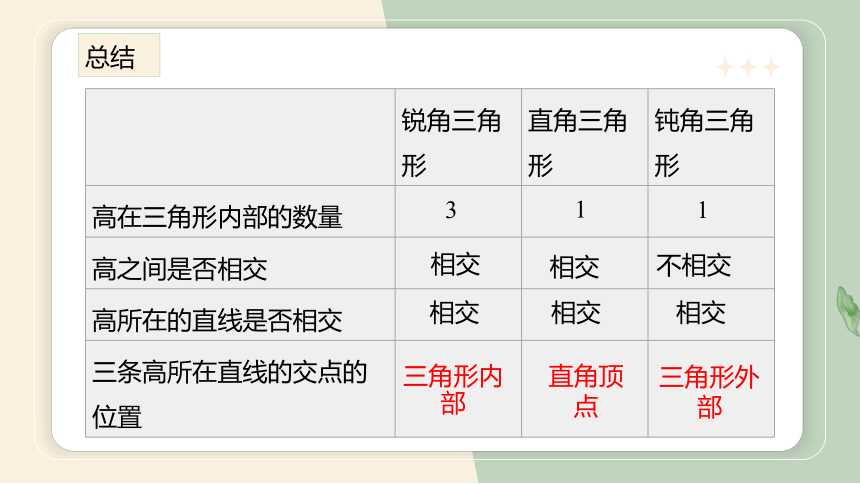
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在直线的交点的位置
3
1
1
相交
相交
不相交
相交
相交
相交
三角形内部
直角顶点
三角形外部
总结
C
A
B
C
定义:连接三角形的一个顶点和它所对的边的中点,所得线段叫做三角形的这条边上的中线.如图,AD就是△ABC的中线.
几何表达形式:如图,AD是△ABC的边BC上的中线,或点 D 是边 BC 的中点或 BD = CD = BC
三角形的中线将这个三角形分为面积相等的两个三角形
三角形的中线是一条线段
D
画一画:分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
A
B
C
D
E
F
A
B
C
锐角三角形
直角三角形
A
B
C
钝角三角形
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心.
A
准备一个三角形纸片ABC,按图所示的方法折叠,展开后,折痕AD把 ∠ABC 分成∠1和∠2两个角.∠1和∠2有什么关系?
C
A
B
C
A
B
D
C'
三角形的角平分线:在三角形中,一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
几何表达形式:如图,AD是△ABC的角平分线,或AD平分∠BAC交BC于点D,或∠BAD =∠CAD = ∠BAC.
注意:三角形的角平分线是一条线段,而角的平分线是一条射线.
C
A
B
1
2
D
C
A
B
D
F
F
A
B
C
C
B
A
锐角三角形
直角三角形
钝角三角形
三角形的三条角平分线在三角形的内部交于一点.
画一画:分别画出锐角三角形、直角三角形、钝角三角形的三条角平分线,并观察它们中线的交点有什么规律?
CD
∠BCE
BC
∠ACB
B
B
B
D
高线
中线
角平分线
从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段,叫作三角形的高线,简称三角形的高.
在三角形中,连接一个顶点与它对边的中点的线段叫做三角形的中线
在三角形中,一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线
三 角 形
小结
谢谢观看
11.1.2 三角形的高、中线与角平分线
第十一章——三角形
CONTENTS
了解三角形的高、中线与角平分线的概念;
了解三角形的重心的概念;
能正确画出一个三角形的高、中线、角平分线,并掌握其相关性质.
01
02
03
回顾我们之前所学的垂线、线段中点、角平分线的概念
垂线:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
线段中点:把一条线段分成两条相等的线段的点
角平分线:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
怎样“过一点画已知直线的垂线”?
1.放
2.靠
3.过
4.画
通过对垂线的复习,我们进一步学习本节知识涉及到的三角形的高线
三角形的高是一条垂线段
从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段,叫作三角形的高线,简称三角形的高.
A
B
C
D
注意标明垂直的记号和垂足的字母
几何语言:
①AD是△ABC的边BC上的高.
②AD⊥BC,垂足为D.
你还能画出三角形其它边上的高吗?
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
观察图形,你发现了什么?
锐角三角形的三条高都在三角形的内部.
这个结论对所有的三角形都成立吗?
A
B
C
D
E
F
试着作出直角三角形、钝角三角形的三条高.
A
B
C
D
锐角三角形
直角三角形
A
B
C
D
钝角三角形
E
F
直角三角形的两条高与直角边重合,另外一条高在内部
三条高的交点为直角顶点.
钝角三角形的两条高在外部,另外一条高在内部
三条高没有交点,但三条高所在直线交于三角形外一点.
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在直线的交点的位置
3
1
1
相交
相交
不相交
相交
相交
相交
三角形内部
直角顶点
三角形外部
总结
C
A
B
C
定义:连接三角形的一个顶点和它所对的边的中点,所得线段叫做三角形的这条边上的中线.如图,AD就是△ABC的中线.
几何表达形式:如图,AD是△ABC的边BC上的中线,或点 D 是边 BC 的中点或 BD = CD = BC
三角形的中线将这个三角形分为面积相等的两个三角形
三角形的中线是一条线段
D
画一画:分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
A
B
C
D
E
F
A
B
C
锐角三角形
直角三角形
A
B
C
钝角三角形
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心.
A
准备一个三角形纸片ABC,按图所示的方法折叠,展开后,折痕AD把 ∠ABC 分成∠1和∠2两个角.∠1和∠2有什么关系?
C
A
B
C
A
B
D
C'
三角形的角平分线:在三角形中,一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
几何表达形式:如图,AD是△ABC的角平分线,或AD平分∠BAC交BC于点D,或∠BAD =∠CAD = ∠BAC.
注意:三角形的角平分线是一条线段,而角的平分线是一条射线.
C
A
B
1
2
D
C
A
B
D
F
F
A
B
C
C
B
A
锐角三角形
直角三角形
钝角三角形
三角形的三条角平分线在三角形的内部交于一点.
画一画:分别画出锐角三角形、直角三角形、钝角三角形的三条角平分线,并观察它们中线的交点有什么规律?
CD
∠BCE
BC
∠ACB
B
B
B
D
高线
中线
角平分线
从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段,叫作三角形的高线,简称三角形的高.
在三角形中,连接一个顶点与它对边的中点的线段叫做三角形的中线
在三角形中,一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线
三 角 形
小结
谢谢观看
