初中数学人教版八年级上册11.2.1三角形的内角 教学课件(共26张PPT)
文档属性
| 名称 | 初中数学人教版八年级上册11.2.1三角形的内角 教学课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 17.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 18:29:36 | ||
图片预览



文档简介
(共26张PPT)
11.2.1三角形的内角
第十一章——三角形
CONTENTS
了解并掌握三角形的内角和定理;
了解直角三角形两个锐角的关系;
掌握直角三角形的判定方法.
01
02
03
我们在小学就已经知道,任意一个三角形的内角和等于180°. 当时我们是通过度量或剪拼得出这一结论的,可是这种方法不能完全让人信服,所以我们需要通过推理的方法去证明这一定理.下面开始本节知识的学习.
剪刀
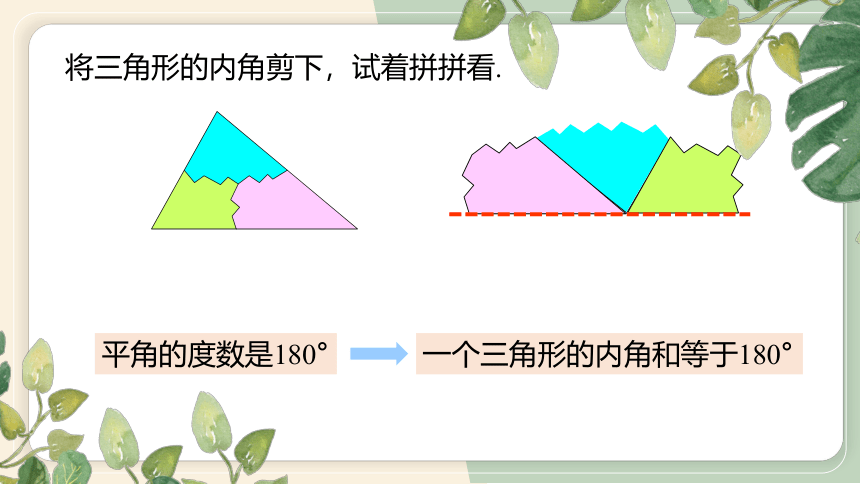
将三角形的内角剪下,试着拼拼看.
平角的度数是180°
一个三角形的内角和等于180°
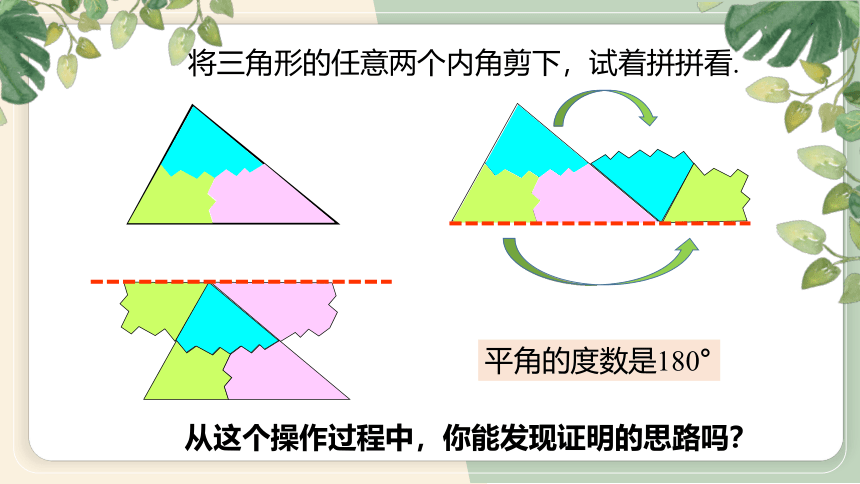
将三角形的任意两个内角剪下,试着拼拼看.
从这个操作过程中,你能发现证明的思路吗?
平角的度数是180°
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
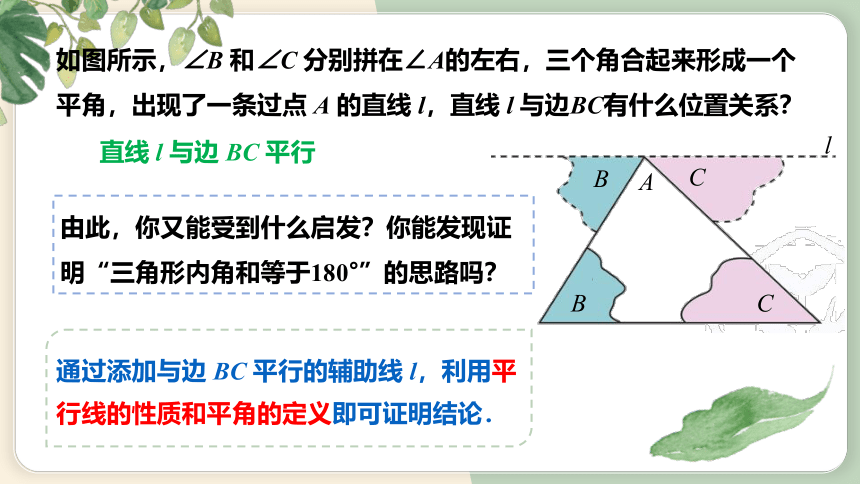
直线 l 与边 BC 平行
B
B
C
C
A
l
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
通过添加与边 BC 平行的辅助线 l,利用平行线的性质和平角的定义即可证明结论.
如图所示,∠B 和∠C 分别拼在∠A的左右,三个角合起来形成一个平角,出现了一条过点 A 的直线 l,直线 l 与边BC有什么位置关系?
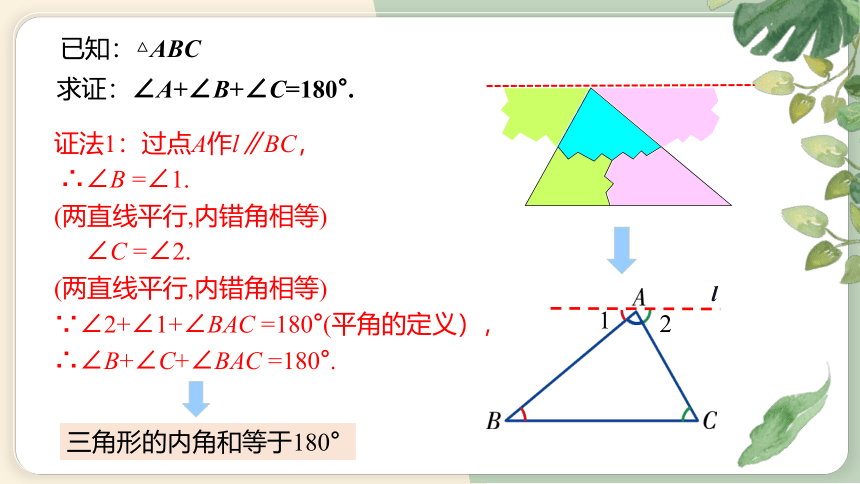
求证:∠A+∠B+∠C=180°.
已知:△ABC
证法1:过点A作l∥BC,
∴∠B =∠1.
(两直线平行,内错角相等)
∠C =∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC =180°(平角的定义),
∴∠B+∠C+∠BAC =180°.
1
2
三角形的内角和等于180°
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
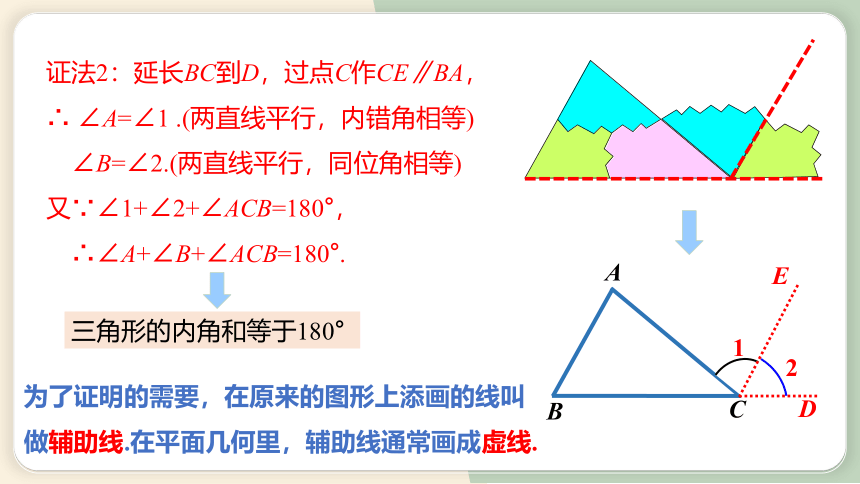
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .(两直线平行,内错角相等)
∠B=∠2.(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
三角形的内角和等于180°
例题练习
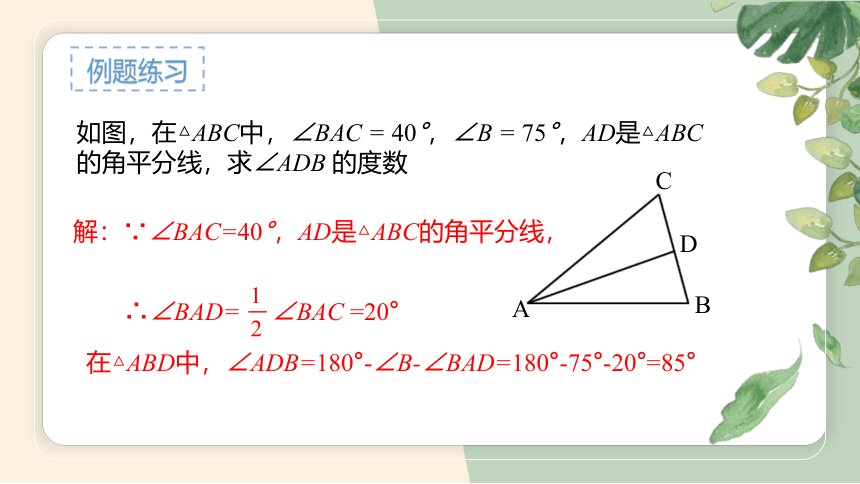
如图,在△ABC中,∠BAC = 40°,∠B = 75°,AD是△ABC 的角平分线,求∠ADB 的度数
解:∵∠BAC=40°,AD是△ABC的角平分线,
∴∠BAD= ∠BAC =20°
在△ABD中,∠ADB=180°-∠B-∠BAD=180°-75°-20°=85°
C
B
D
A
如图是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向.从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
北
北
C
A
B
D
E
分析:∠ACB是△ABC的一个内角,
求∠ACB需先求 ∠CAB 、∠CBA.
例题练习
解: ∠CAB= ∠BAD- ∠CAD=80 °-50°=30°.
由 AD//BE,得∠BAD+ ∠ABE=180 °.
所以∠ABE=180 °- ∠BAD=180°-80°=100°,
∠ABC= ∠ABE- ∠EBC=100°-40°=60°.
在△ABC中,∠ACB=180 °- ∠ABC- ∠ CAB=180°-60°-30° =90°,
答:从B岛看A,C两岛的视角∠ABC是60 °,从C岛看A,B两岛的视角
∠ACB是90°.
∠C=90°
如图,在直角△ABC 中,∠C=90°,两锐角的和等于多少?
三角形内角和定理
∠A +∠B +∠C=180°
∠A + ∠B=90°
∠C=90°
∠A +∠B +90°=180°
直角三角形的性质:
直角三角形的两个锐角_____.
互余
几何语言:
在 Rt△ABC 中,
∵∠C=90°,
∴∠A +∠B=90°.
“Rt△”
如图,∠C=∠D=90°,AD,BC 相交于点E.∠CAE与∠DBE有什么关系?说明理由.
解:∠CAE=∠DBE.
理由如下:在 Rt △ACE 中,∠CAE=90°-∠AEC.
在 Rt △BDE 中,∠DBE=90°-∠BED.
∵∠AEC=∠BED,∴∠CAE=∠DBE.
例题练习
【思考】如果一个三角形的直角三角形,那么这个三角形有两个角互余,反之,有两个角互余的三角形是直角三角形吗?
如图,在 △ABC 中,∠A +∠B=90°, 那么△ABC 是直角三角形吗?
三角形内角和定理
∠A +∠B +∠C=180°
∠C + 90°=180°
∠A +∠B=90°
∴△ABC 是直角三角形
∠C = 90°
直角三角形的判定:
有两个角_____的三角形是直角三角形.
互余
几何语言:
在△ABC 中,
∵∠A +∠B=90°,
∴△ABC 是直角三角形.
C
A
B
B
直角
45°
三角形内角和定理:三角三个内角的和等于180°
直角三角形的两个锐角互余
有两个角互余的三角形是直角三角形
三角形的内角
小结
谢谢观看
11.2.1三角形的内角
第十一章——三角形
CONTENTS
了解并掌握三角形的内角和定理;
了解直角三角形两个锐角的关系;
掌握直角三角形的判定方法.
01
02
03
我们在小学就已经知道,任意一个三角形的内角和等于180°. 当时我们是通过度量或剪拼得出这一结论的,可是这种方法不能完全让人信服,所以我们需要通过推理的方法去证明这一定理.下面开始本节知识的学习.
剪刀
将三角形的内角剪下,试着拼拼看.
平角的度数是180°
一个三角形的内角和等于180°
将三角形的任意两个内角剪下,试着拼拼看.
从这个操作过程中,你能发现证明的思路吗?
平角的度数是180°
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
直线 l 与边 BC 平行
B
B
C
C
A
l
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
通过添加与边 BC 平行的辅助线 l,利用平行线的性质和平角的定义即可证明结论.
如图所示,∠B 和∠C 分别拼在∠A的左右,三个角合起来形成一个平角,出现了一条过点 A 的直线 l,直线 l 与边BC有什么位置关系?
求证:∠A+∠B+∠C=180°.
已知:△ABC
证法1:过点A作l∥BC,
∴∠B =∠1.
(两直线平行,内错角相等)
∠C =∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC =180°(平角的定义),
∴∠B+∠C+∠BAC =180°.
1
2
三角形的内角和等于180°
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .(两直线平行,内错角相等)
∠B=∠2.(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
三角形的内角和等于180°
例题练习
如图,在△ABC中,∠BAC = 40°,∠B = 75°,AD是△ABC 的角平分线,求∠ADB 的度数
解:∵∠BAC=40°,AD是△ABC的角平分线,
∴∠BAD= ∠BAC =20°
在△ABD中,∠ADB=180°-∠B-∠BAD=180°-75°-20°=85°
C
B
D
A
如图是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向.从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
北
北
C
A
B
D
E
分析:∠ACB是△ABC的一个内角,
求∠ACB需先求 ∠CAB 、∠CBA.
例题练习
解: ∠CAB= ∠BAD- ∠CAD=80 °-50°=30°.
由 AD//BE,得∠BAD+ ∠ABE=180 °.
所以∠ABE=180 °- ∠BAD=180°-80°=100°,
∠ABC= ∠ABE- ∠EBC=100°-40°=60°.
在△ABC中,∠ACB=180 °- ∠ABC- ∠ CAB=180°-60°-30° =90°,
答:从B岛看A,C两岛的视角∠ABC是60 °,从C岛看A,B两岛的视角
∠ACB是90°.
∠C=90°
如图,在直角△ABC 中,∠C=90°,两锐角的和等于多少?
三角形内角和定理
∠A +∠B +∠C=180°
∠A + ∠B=90°
∠C=90°
∠A +∠B +90°=180°
直角三角形的性质:
直角三角形的两个锐角_____.
互余
几何语言:
在 Rt△ABC 中,
∵∠C=90°,
∴∠A +∠B=90°.
“Rt△”
如图,∠C=∠D=90°,AD,BC 相交于点E.∠CAE与∠DBE有什么关系?说明理由.
解:∠CAE=∠DBE.
理由如下:在 Rt △ACE 中,∠CAE=90°-∠AEC.
在 Rt △BDE 中,∠DBE=90°-∠BED.
∵∠AEC=∠BED,∴∠CAE=∠DBE.
例题练习
【思考】如果一个三角形的直角三角形,那么这个三角形有两个角互余,反之,有两个角互余的三角形是直角三角形吗?
如图,在 △ABC 中,∠A +∠B=90°, 那么△ABC 是直角三角形吗?
三角形内角和定理
∠A +∠B +∠C=180°
∠C + 90°=180°
∠A +∠B=90°
∴△ABC 是直角三角形
∠C = 90°
直角三角形的判定:
有两个角_____的三角形是直角三角形.
互余
几何语言:
在△ABC 中,
∵∠A +∠B=90°,
∴△ABC 是直角三角形.
C
A
B
B
直角
45°
三角形内角和定理:三角三个内角的和等于180°
直角三角形的两个锐角互余
有两个角互余的三角形是直角三角形
三角形的内角
小结
谢谢观看
