初中数学人教版八年级上册11.3.2多边形的内角和 教学课件(共23张PPT)
文档属性
| 名称 | 初中数学人教版八年级上册11.3.2多边形的内角和 教学课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 22.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 18:38:30 | ||
图片预览





文档简介
(共23张PPT)
11.3.2多边形的内角和
第十一章——三角形
CONTENTS
掌握多边形的内角和公式;
应用多边形的内角和与外角和公式解决问题
01
02
03
掌握多边形的外角和等于360°;
学习目标
1.从 n (n ≥ 3) 边形的一个顶点可以作出________条对角线,将多边形分成______个三角形.
2.n (n≥3) 边形共有对角线_________条.
(n - 3)
(n - 2)
知识回顾
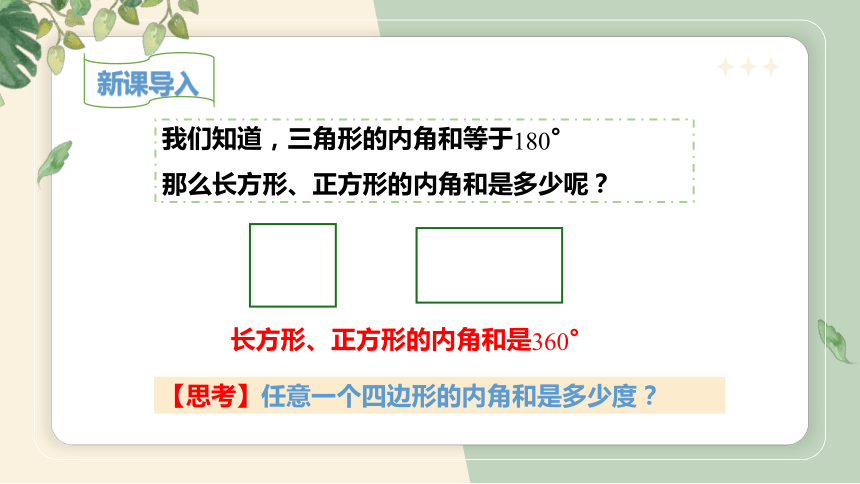
新课导入
我们知道,三角形的内角和等于180°
那么长方形、正方形的内角和是多少呢?
长方形、正方形的内角和是360°
【思考】任意一个四边形的内角和是多少度?
剪刀
你能利用三角形内角和定理证明你的猜想是否正确吗?
【猜想】任意一个四边形的内角和是360°
从四边形的一个顶点出发,
可以作_____条对角线,它们将
四边形分为 个三角形,
四边形的内角和等于180°×____= .
1
2
2
360°
A
B
C
D
A
B
C
D
E
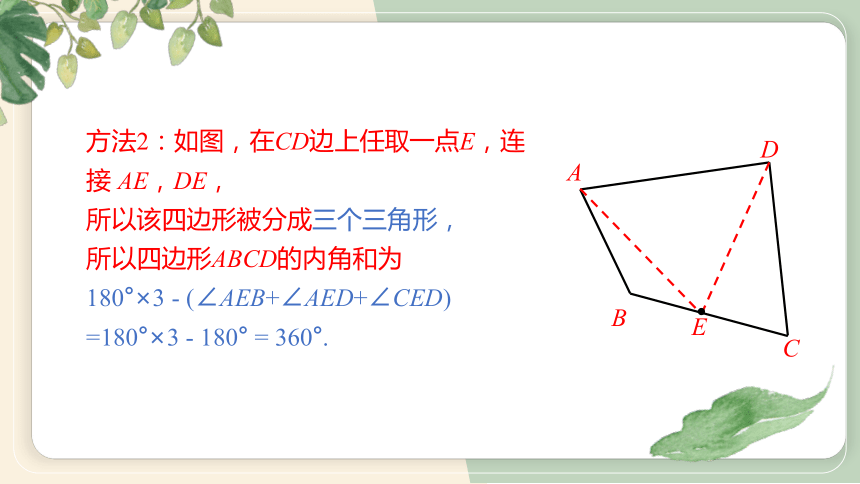
方法2:如图,在CD边上任取一点E,连接 AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3 - (∠AEB+∠AED+∠CED)
=180°×3 - 180° = 360°.
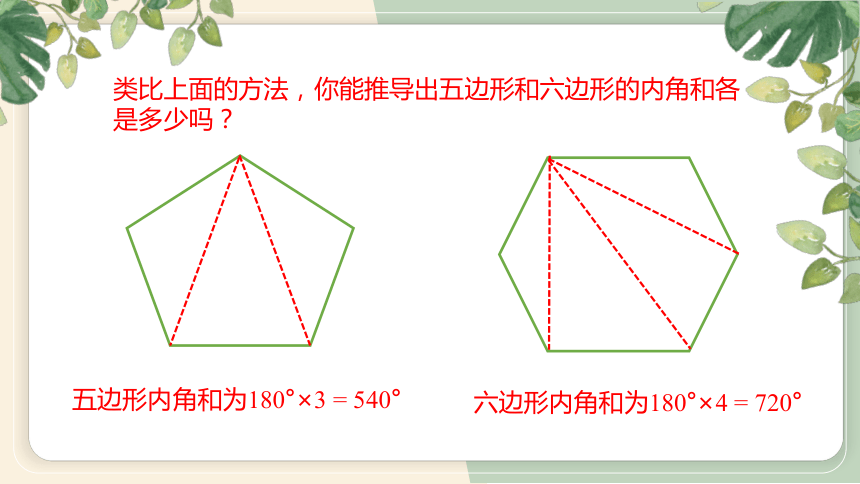
类比上面的方法,你能推导出五边形和六边形的内角和各是多少吗?
五边形内角和为180°×3 = 540°
六边形内角和为180°×4 = 720°
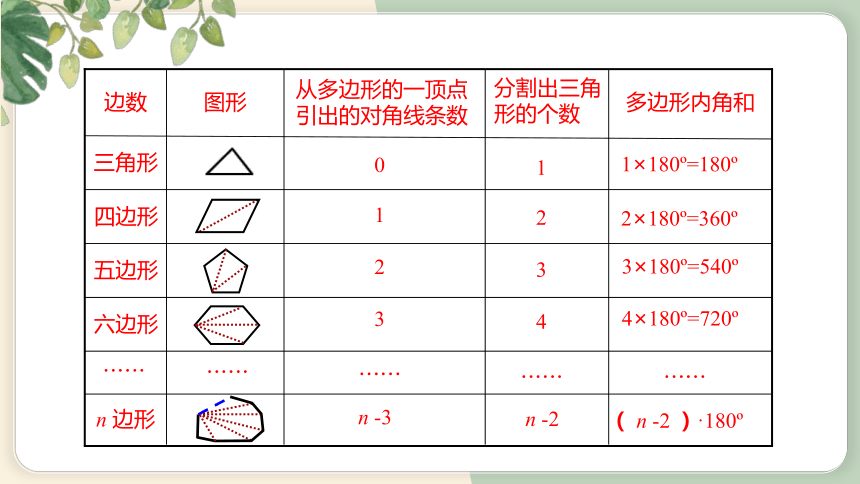
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
0
n -3
1
2
3
1
2
3
4
n -2
( n -2 )·180
1×180 =180
2×180 =360
3×180 =540
4×180 =720
······
······
······
······
【总结】
分割
多边形
三角形
转化思想
多边形内角和公式:n边形内角和等于(n-2)×180 °.
例题练习
如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
如图,在四边形 ABCD 中,
∠A +∠C = 180°.
∵ ∠A +∠B +∠C +∠D = 360°,
∴ ∠B +∠D = 360° - (∠A +∠C )
= 360° - 180° = 180°.
如果一个四边形的一组对角互补,那么另一组对角也互补.
如图,在六边形的每个顶点处取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
问题1:任意一个外角和它相邻的内角有什么关系?
互补
问题2:六边形的6个外角加上与它们相邻的内角,所得总和是多少?
6×180°=1080°
如图,在六边形的各个顶点处取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
因此六边形的外角和
= 360 °
= 总和 - 六边形内角和
= 6×180° - (6-2) × 180°
结论:六边形的外角和等于360°.
问题3:上述总和六边形的内角和、外角和有什么关系?
六边形的外角和加上内角和等于这个总和
将六边形换成n边形(n是不小于3的任意整数)可以得到同样的结果吗?
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
= 360 °
= n边形内外角总和 - n边形内角和
= n×180 °- (n-2) × 180°
n边形的外角和等于360°.
与边数无关
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
A
B
C
D
E
1
2
3
4
5
如图,从多边形的一个顶点A出发,沿着多边形的各边走过各顶点,再回到点A,然后转向出发时的方向.在行程中所转的各个角的和,就是多边形的外角和.由于走了一周,所转的各个角的和等于一个周角,所以多边形的外角和等于360°
B
B
C
C
10
多边形的内角和等于
________________
多边形的外角和等于______
多边形
小结
(n - 2)×180°
360°
谢谢观看
11.3.2多边形的内角和
第十一章——三角形
CONTENTS
掌握多边形的内角和公式;
应用多边形的内角和与外角和公式解决问题
01
02
03
掌握多边形的外角和等于360°;
学习目标
1.从 n (n ≥ 3) 边形的一个顶点可以作出________条对角线,将多边形分成______个三角形.
2.n (n≥3) 边形共有对角线_________条.
(n - 3)
(n - 2)
知识回顾
新课导入
我们知道,三角形的内角和等于180°
那么长方形、正方形的内角和是多少呢?
长方形、正方形的内角和是360°
【思考】任意一个四边形的内角和是多少度?
剪刀
你能利用三角形内角和定理证明你的猜想是否正确吗?
【猜想】任意一个四边形的内角和是360°
从四边形的一个顶点出发,
可以作_____条对角线,它们将
四边形分为 个三角形,
四边形的内角和等于180°×____= .
1
2
2
360°
A
B
C
D
A
B
C
D
E
方法2:如图,在CD边上任取一点E,连接 AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3 - (∠AEB+∠AED+∠CED)
=180°×3 - 180° = 360°.
类比上面的方法,你能推导出五边形和六边形的内角和各是多少吗?
五边形内角和为180°×3 = 540°
六边形内角和为180°×4 = 720°
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
0
n -3
1
2
3
1
2
3
4
n -2
( n -2 )·180
1×180 =180
2×180 =360
3×180 =540
4×180 =720
······
······
······
······
【总结】
分割
多边形
三角形
转化思想
多边形内角和公式:n边形内角和等于(n-2)×180 °.
例题练习
如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
如图,在四边形 ABCD 中,
∠A +∠C = 180°.
∵ ∠A +∠B +∠C +∠D = 360°,
∴ ∠B +∠D = 360° - (∠A +∠C )
= 360° - 180° = 180°.
如果一个四边形的一组对角互补,那么另一组对角也互补.
如图,在六边形的每个顶点处取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
问题1:任意一个外角和它相邻的内角有什么关系?
互补
问题2:六边形的6个外角加上与它们相邻的内角,所得总和是多少?
6×180°=1080°
如图,在六边形的各个顶点处取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
因此六边形的外角和
= 360 °
= 总和 - 六边形内角和
= 6×180° - (6-2) × 180°
结论:六边形的外角和等于360°.
问题3:上述总和六边形的内角和、外角和有什么关系?
六边形的外角和加上内角和等于这个总和
将六边形换成n边形(n是不小于3的任意整数)可以得到同样的结果吗?
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
= 360 °
= n边形内外角总和 - n边形内角和
= n×180 °- (n-2) × 180°
n边形的外角和等于360°.
与边数无关
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
A
B
C
D
E
1
2
3
4
5
如图,从多边形的一个顶点A出发,沿着多边形的各边走过各顶点,再回到点A,然后转向出发时的方向.在行程中所转的各个角的和,就是多边形的外角和.由于走了一周,所转的各个角的和等于一个周角,所以多边形的外角和等于360°
B
B
C
C
10
多边形的内角和等于
________________
多边形的外角和等于______
多边形
小结
(n - 2)×180°
360°
谢谢观看
