初中数学人教版八年级上册11.2.2三角形的外角 教学课件(共24张PPT)
文档属性
| 名称 | 初中数学人教版八年级上册11.2.2三角形的外角 教学课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 31.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 18:40:53 | ||
图片预览



文档简介
(共24张PPT)
11.2.2三角形的外角
第十一章——三角形
CONTENTS
理解三角形的外角的概念;
理解并掌握三角形的外角的性质;
能够在图形中找到三角形的外角;
01
02
03
04
了解三角形的外角和.
教学目标
2.在△ABC中,∠A=85°, ∠B=44°,则∠C= .
3.在△ABC中,∠A=22°, ∠B=76°,则∠C= .
82 °
51 °
1.什么是三角形的内角?三角形内角和定理是什么?
三角形相邻两边组成的角叫作三角形的内角
三角形三个内角的和等于180°
复习导入
剪刀
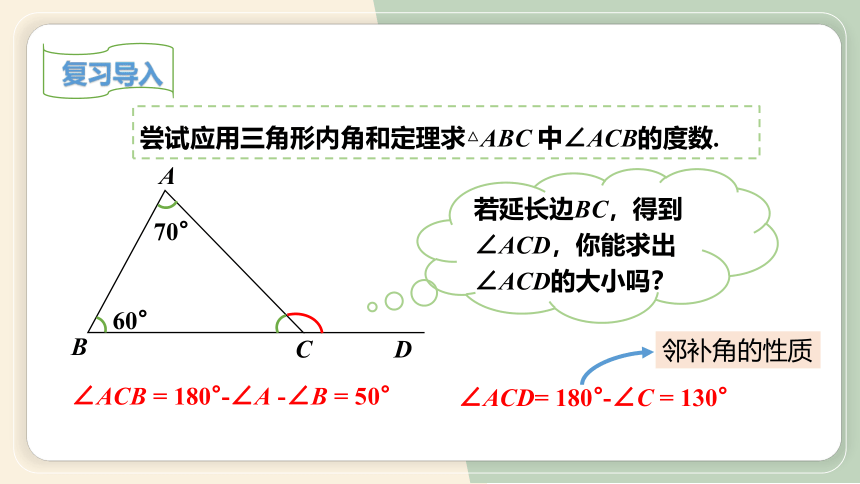
尝试应用三角形内角和定理求△ABC 中∠ACB的度数.
60°
70°
B
A
C
∠ACB = 180°-∠A -∠B = 50°
D
若延长边BC,得到∠ACD,你能求出∠ACD的大小吗?
∠ACD= 180°-∠C = 130°
邻补角的性质
复习导入
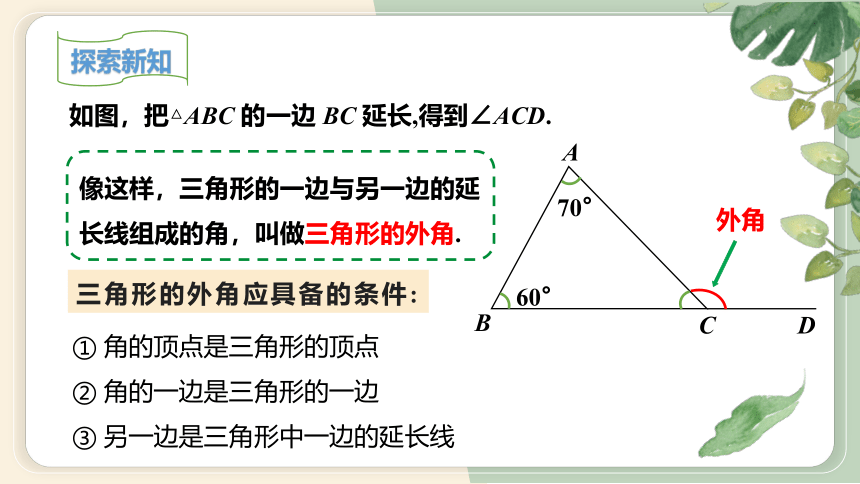
像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
外角
如图,把△ABC 的一边 BC 延长,得到∠ACD.
探索新知
60°
70°
B
A
C
D
三角形的外角应具备的条件:
① 角的顶点是三角形的顶点
② 角的一边是三角形的一边
③ 另一边是三角形中一边的延长线
F
A
B
C
D
E
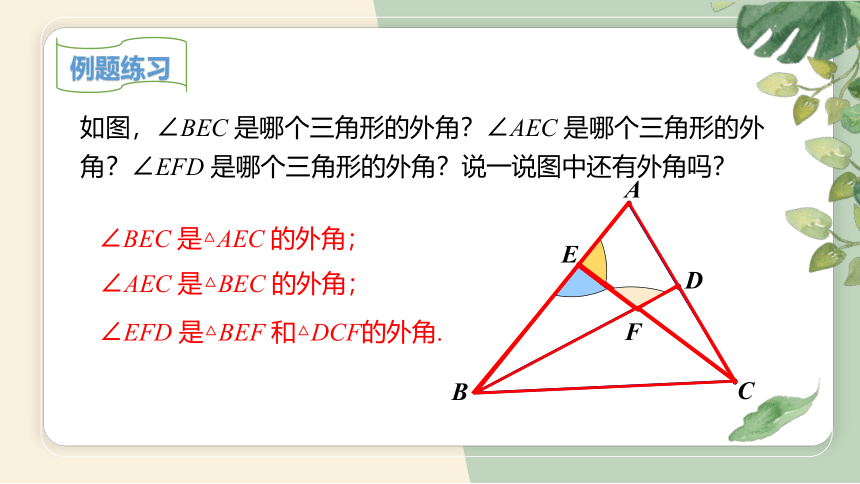
如图,∠BEC 是哪个三角形的外角?∠AEC 是哪个三角形的外角?∠EFD 是哪个三角形的外角?说一说图中还有外角吗?
∠BEC 是△AEC 的外角;
∠AEC 是△BEC 的外角;
∠EFD 是△BEF 和△DCF的外角.
例题练习
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
每个顶点处有几个外角?它们有何关系?
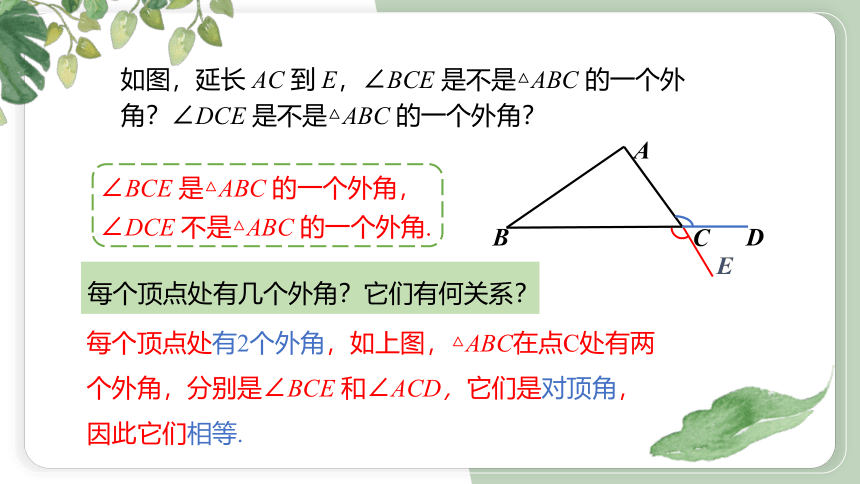
如图,延长 AC 到 E,∠BCE 是不是△ABC 的一个外角?∠DCE 是不是△ABC 的一个外角?
E
C
B
A
D
∠BCE 是△ABC 的一个外角,∠DCE 不是△ABC 的一个外角.
每个顶点处有2个外角,如上图,△ABC在点C处有两个外角,分别是∠BCE 和∠ACD,它们是对顶角,因此它们相等.
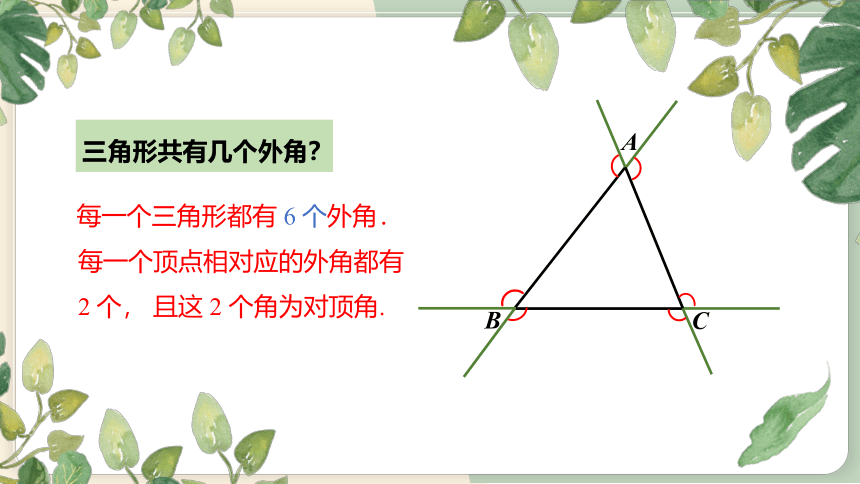
三角形共有几个外角?
每一个三角形都有 6 个外角.
每一个顶点相对应的外角都有 2 个, 且这 2 个角为对顶角.
A
B
C
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
D
C
B
A
60°
70°
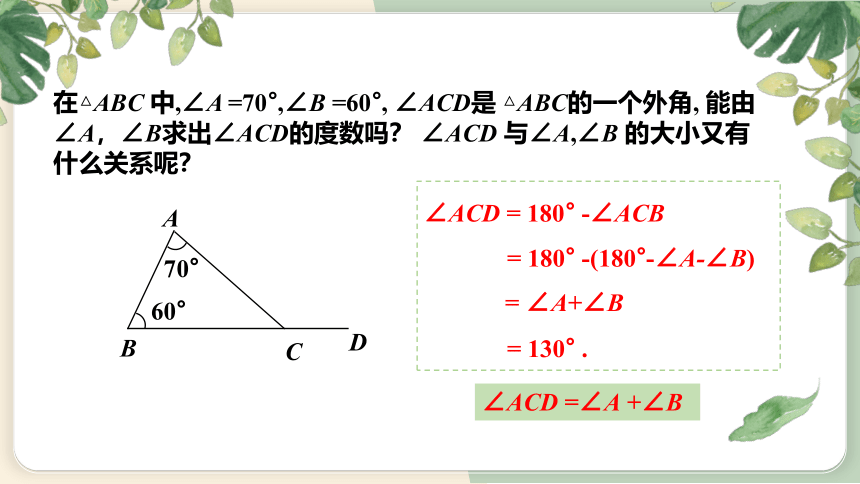
∠ACD = 180° -∠ACB
= 180° -(180°-∠A-∠B)
= ∠A+∠B
= 130° .
∠ACD =∠A +∠B
在△ABC 中,∠A =70°,∠B =60°, ∠ACD是 △ABC的一个外角, 能由∠A,∠B求出∠ACD的度数吗? ∠ACD 与∠A,∠B 的大小又有什么关系呢?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
证明1:
∵∠A +∠B+∠ACB=180°,∠BCD +∠ACB=180°
∴∠A+∠B=∠BCD.
你还能用其他方法证明此结论吗?
如图,任意一个△ABC 的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
D
证明2:过 C 作 CE 平行于 AB,
A
B
C
1
2
∴∠ACD = ∠1+ ∠2 = ∠A+ ∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
∴∠1= ∠B,
(两直线平行,同位角相等)
∠2= ∠A ,
(两直线平行,内错角相等)
一般地,由三角形内角和定理可以推出下面的推论:
三角形的外角等于与它不相邻的两个内角的和.
符号语言
∵∠ACD 是△ABC 的外角,
∴∠ACD = ∠A +∠B.
D
C
B
A
∠BCD >∠A,∠BCD >∠B .
由推论可知 ∠BCD =∠A+∠B
因此
三角形的一个外角大于任何一个与它不相邻的内角.
推论是由定理直接推出的结论.和定理一样,推论可以作为进一步推理的依据.
如图,∠BAE,∠CBF,∠ACD是△ABC 的三个外角,它们的和是多少?
D
C
B
A
1
3
2
E
F
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE =∠2 +∠3,
∠CBF =∠1 +∠3,
∠ACD =∠1 +∠2,
∴∠BAE +∠CBF +∠ACD= 2(∠1 +∠2 +∠3).
由∠1 +∠2 +∠3 = 180°,得
∴ ∠BAE +∠CBF +∠ACD =2× 180°=360°.
你还有其他解法吗?
例题练习
如图,∠BAE,∠CBF,∠ACD是△ABC 的三个外角,它们的和是多少?
解法二:如图,∠BAE+∠1=180 ° ① ,
∠CBF +∠2=180 ° ②,
∠ACD +∠3=180 ° ③,
又知∠1+ ∠2+ ∠3=180 °,
①+ ②+ ③得
∠BAE + ∠CBF + ∠ACD +(∠1+ ∠2+ ∠3) = 540 °,
所以∠BAE + ∠CBF + ∠ACD = 540 °- 180°= 360°.
例题练习
D
C
B
A
1
3
2
E
F
三角形的每个顶点处有两个外角,它们相等,所以每个顶点处只取一个外角(按同一个方向取三个角),把它们的和叫做三角形的外角和.
三角形的外角和等于 360°.
D
C
B
A
1
3
2
E
F
D
B
B
F
D
235
定义:三角形的一边与另外一边的延长线所组成的角
性质:三角形的一个外角等于与它不相邻的两个内角的和
三角形外角和:三角形的外角和等于360°
三角形的外角
小结
谢谢观看
11.2.2三角形的外角
第十一章——三角形
CONTENTS
理解三角形的外角的概念;
理解并掌握三角形的外角的性质;
能够在图形中找到三角形的外角;
01
02
03
04
了解三角形的外角和.
教学目标
2.在△ABC中,∠A=85°, ∠B=44°,则∠C= .
3.在△ABC中,∠A=22°, ∠B=76°,则∠C= .
82 °
51 °
1.什么是三角形的内角?三角形内角和定理是什么?
三角形相邻两边组成的角叫作三角形的内角
三角形三个内角的和等于180°
复习导入
剪刀
尝试应用三角形内角和定理求△ABC 中∠ACB的度数.
60°
70°
B
A
C
∠ACB = 180°-∠A -∠B = 50°
D
若延长边BC,得到∠ACD,你能求出∠ACD的大小吗?
∠ACD= 180°-∠C = 130°
邻补角的性质
复习导入
像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
外角
如图,把△ABC 的一边 BC 延长,得到∠ACD.
探索新知
60°
70°
B
A
C
D
三角形的外角应具备的条件:
① 角的顶点是三角形的顶点
② 角的一边是三角形的一边
③ 另一边是三角形中一边的延长线
F
A
B
C
D
E
如图,∠BEC 是哪个三角形的外角?∠AEC 是哪个三角形的外角?∠EFD 是哪个三角形的外角?说一说图中还有外角吗?
∠BEC 是△AEC 的外角;
∠AEC 是△BEC 的外角;
∠EFD 是△BEF 和△DCF的外角.
例题练习
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
每个顶点处有几个外角?它们有何关系?
如图,延长 AC 到 E,∠BCE 是不是△ABC 的一个外角?∠DCE 是不是△ABC 的一个外角?
E
C
B
A
D
∠BCE 是△ABC 的一个外角,∠DCE 不是△ABC 的一个外角.
每个顶点处有2个外角,如上图,△ABC在点C处有两个外角,分别是∠BCE 和∠ACD,它们是对顶角,因此它们相等.
三角形共有几个外角?
每一个三角形都有 6 个外角.
每一个顶点相对应的外角都有 2 个, 且这 2 个角为对顶角.
A
B
C
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
D
C
B
A
60°
70°
∠ACD = 180° -∠ACB
= 180° -(180°-∠A-∠B)
= ∠A+∠B
= 130° .
∠ACD =∠A +∠B
在△ABC 中,∠A =70°,∠B =60°, ∠ACD是 △ABC的一个外角, 能由∠A,∠B求出∠ACD的度数吗? ∠ACD 与∠A,∠B 的大小又有什么关系呢?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
证明1:
∵∠A +∠B+∠ACB=180°,∠BCD +∠ACB=180°
∴∠A+∠B=∠BCD.
你还能用其他方法证明此结论吗?
如图,任意一个△ABC 的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
D
证明2:过 C 作 CE 平行于 AB,
A
B
C
1
2
∴∠ACD = ∠1+ ∠2 = ∠A+ ∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
∴∠1= ∠B,
(两直线平行,同位角相等)
∠2= ∠A ,
(两直线平行,内错角相等)
一般地,由三角形内角和定理可以推出下面的推论:
三角形的外角等于与它不相邻的两个内角的和.
符号语言
∵∠ACD 是△ABC 的外角,
∴∠ACD = ∠A +∠B.
D
C
B
A
∠BCD >∠A,∠BCD >∠B .
由推论可知 ∠BCD =∠A+∠B
因此
三角形的一个外角大于任何一个与它不相邻的内角.
推论是由定理直接推出的结论.和定理一样,推论可以作为进一步推理的依据.
如图,∠BAE,∠CBF,∠ACD是△ABC 的三个外角,它们的和是多少?
D
C
B
A
1
3
2
E
F
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE =∠2 +∠3,
∠CBF =∠1 +∠3,
∠ACD =∠1 +∠2,
∴∠BAE +∠CBF +∠ACD= 2(∠1 +∠2 +∠3).
由∠1 +∠2 +∠3 = 180°,得
∴ ∠BAE +∠CBF +∠ACD =2× 180°=360°.
你还有其他解法吗?
例题练习
如图,∠BAE,∠CBF,∠ACD是△ABC 的三个外角,它们的和是多少?
解法二:如图,∠BAE+∠1=180 ° ① ,
∠CBF +∠2=180 ° ②,
∠ACD +∠3=180 ° ③,
又知∠1+ ∠2+ ∠3=180 °,
①+ ②+ ③得
∠BAE + ∠CBF + ∠ACD +(∠1+ ∠2+ ∠3) = 540 °,
所以∠BAE + ∠CBF + ∠ACD = 540 °- 180°= 360°.
例题练习
D
C
B
A
1
3
2
E
F
三角形的每个顶点处有两个外角,它们相等,所以每个顶点处只取一个外角(按同一个方向取三个角),把它们的和叫做三角形的外角和.
三角形的外角和等于 360°.
D
C
B
A
1
3
2
E
F
D
B
B
F
D
235
定义:三角形的一边与另外一边的延长线所组成的角
性质:三角形的一个外角等于与它不相邻的两个内角的和
三角形外角和:三角形的外角和等于360°
三角形的外角
小结
谢谢观看
