12.2三角形全等的判定(第四课时)教学课件(共19张PPT)初中数学人教版八年级上册
文档属性
| 名称 | 12.2三角形全等的判定(第四课时)教学课件(共19张PPT)初中数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 16.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 20:08:32 | ||
图片预览






文档简介
(共19张PPT)
12.2三角形全等的判定(第四课时)
第十二章——全等三角形
COTENTS
会用直角三角形全等的判定方法“HL”判定两个直角三角形全等
理解并掌握直角三角形全等的判定方法“HL”;
01
02
学习目标
复习导入
目前我们已经学习了哪些判定两个三角形全等的方法?
3.两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
4.两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.
2.两边和它们的夹角分别相等的两个三角形全等(简写为“边角边”或“SAS”)
1.三边分别相等的两个三角形全等.(简写为“边边边”或“SSS”)
这四种判定方法是否同样适用于直角三角形
1.两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
2.两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?为什么?
A
B
C
A′
B′
C′
AAS 或 ASA
全等
全等
AAS 或 ASA
4.两个直角三角形中,斜边和一条直角边分别相等,这两个直角三角形全等吗?为什么?
A
B
C
A′
B′
C′
SSA
不全等?
SAS
3.两个直角三角形中,两直角边分别相等,这两个直角三角形全等吗?为什么?
全等
【探究】任意画出一个 Rt△ABC,使∠C = 90°. 再画一个 Rt△A′B′C′ ,使∠C′ = 90°,B′C′ = BC,A′B′ = AB,把画好的 Rt△A′B′C′ 剪下来,放到 Rt△ABC 上,它们全等吗?
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
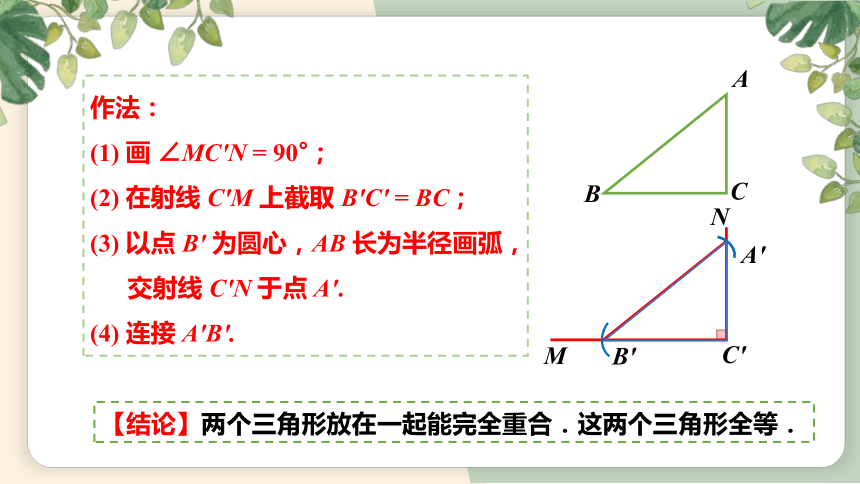
【结论】两个三角形放在一起能完全重合.这两个三角形全等.
作法:
(1) 画 ∠MC'N = 90°;
(2) 在射线 C'M 上截取 B'C' = BC;
(3) 以点 B' 为圆心,AB 长为半径画弧,
交射线 C'N 于点 A'.
(4) 连接 A'B'.
M
C′
N
B′
A′
A
B
C
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【总结】斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
几何语言:
在 Rt△ABC 和 Rt△A′B′C′ 中,
∴ Rt△ABC ≌ Rt△DEF(HL).
AB = A′B′,
BC = B′C′,
C′
B′
A′
A
B
C
例题练习
如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.
求证BC=AD.
A
B
D
C
证明:∵AC⊥BC,BD⊥AD,
∴∠C =∠D = 90°.
在 Rt△ABC 和 Rt△BAD 中,
∴Rt△ABC ≌ Rt△BAD (HL).
∴BC = AD.
应用“HL”的前提条件是在直角三角形中.
一般三角形 已知 方法 特别说明
三边 SSS
两边一角 SAS 其中角为两边的夹角
两角一边 ASA AAS 对于两个三角形只需有两个角和一边
对应相等则其全等
直角三角形 两边 HL SAS 两边可以为斜边和直角边,或两直角边
一边一角 ASA AAS 一角是指除直角之外的另一角
D
C
斜边、直角边
(HL)
小结
斜边和一条直角边分别相等的两个直角三角形全等(HL)
SSS、AAS、ASA、SAS适用于一般三角形; HL只适用于直角三角形.
谢谢观看
12.2三角形全等的判定(第四课时)
第十二章——全等三角形
COTENTS
会用直角三角形全等的判定方法“HL”判定两个直角三角形全等
理解并掌握直角三角形全等的判定方法“HL”;
01
02
学习目标
复习导入
目前我们已经学习了哪些判定两个三角形全等的方法?
3.两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
4.两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.
2.两边和它们的夹角分别相等的两个三角形全等(简写为“边角边”或“SAS”)
1.三边分别相等的两个三角形全等.(简写为“边边边”或“SSS”)
这四种判定方法是否同样适用于直角三角形
1.两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
2.两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?为什么?
A
B
C
A′
B′
C′
AAS 或 ASA
全等
全等
AAS 或 ASA
4.两个直角三角形中,斜边和一条直角边分别相等,这两个直角三角形全等吗?为什么?
A
B
C
A′
B′
C′
SSA
不全等?
SAS
3.两个直角三角形中,两直角边分别相等,这两个直角三角形全等吗?为什么?
全等
【探究】任意画出一个 Rt△ABC,使∠C = 90°. 再画一个 Rt△A′B′C′ ,使∠C′ = 90°,B′C′ = BC,A′B′ = AB,把画好的 Rt△A′B′C′ 剪下来,放到 Rt△ABC 上,它们全等吗?
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【结论】两个三角形放在一起能完全重合.这两个三角形全等.
作法:
(1) 画 ∠MC'N = 90°;
(2) 在射线 C'M 上截取 B'C' = BC;
(3) 以点 B' 为圆心,AB 长为半径画弧,
交射线 C'N 于点 A'.
(4) 连接 A'B'.
M
C′
N
B′
A′
A
B
C
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【总结】斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
几何语言:
在 Rt△ABC 和 Rt△A′B′C′ 中,
∴ Rt△ABC ≌ Rt△DEF(HL).
AB = A′B′,
BC = B′C′,
C′
B′
A′
A
B
C
例题练习
如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.
求证BC=AD.
A
B
D
C
证明:∵AC⊥BC,BD⊥AD,
∴∠C =∠D = 90°.
在 Rt△ABC 和 Rt△BAD 中,
∴Rt△ABC ≌ Rt△BAD (HL).
∴BC = AD.
应用“HL”的前提条件是在直角三角形中.
一般三角形 已知 方法 特别说明
三边 SSS
两边一角 SAS 其中角为两边的夹角
两角一边 ASA AAS 对于两个三角形只需有两个角和一边
对应相等则其全等
直角三角形 两边 HL SAS 两边可以为斜边和直角边,或两直角边
一边一角 ASA AAS 一角是指除直角之外的另一角
D
C
斜边、直角边
(HL)
小结
斜边和一条直角边分别相等的两个直角三角形全等(HL)
SSS、AAS、ASA、SAS适用于一般三角形; HL只适用于直角三角形.
谢谢观看
