12.1全等三角形 教学课件(共25张PPT)初中数学人教版八年级上册
文档属性
| 名称 | 12.1全等三角形 教学课件(共25张PPT)初中数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 18.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 20:08:50 | ||
图片预览






文档简介
(共25张PPT)
12.1全等三角形
第十二章——全等三角形
CONTENTS
了解全等形的概念;
理解并掌握全等三角形的性质.
理解并掌握全等三角形的概念和符号表示;
01
02
03
学习目标
情境导入
有人曾经说:“世界上没有两片完全相同的叶子 ”,但是在我们的日常生活中却有着许多形状、大小完全相同的图形,比如:
你能再举出一些类似的例子吗
剪刀
【探究】把手中的三角形板按在纸上,画出三角形并裁下来,裁下来的三角形纸板与三角尺放在一起形状、大小完全一样吗?能够完全重合吗?
形状、大小完全一样,能够完全重合
1.若两个图形形状、大小完全一样,能够完全重合,他们叫什么?
能够完全重合的两个图形叫做全等形.
2.两个三角形能够完全重合,又叫什么呢
能够完全重合的两个三角形叫做全等三角形.
A
B
C
A
B
C
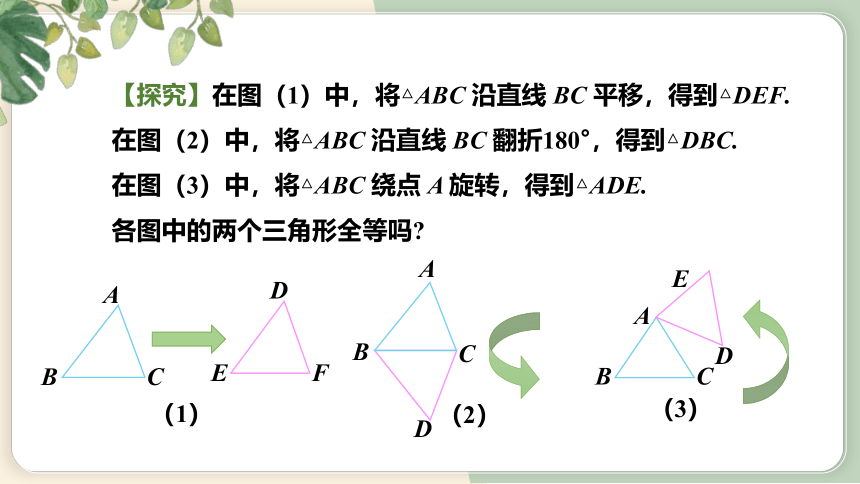
【探究】在图(1)中,将△ABC 沿直线 BC 平移,得到△DEF.
在图(2)中,将△ABC 沿直线 BC 翻折180°,得到△DBC.
在图(3)中,将△ABC 绕点 A 旋转,得到△ADE.
各图中的两个三角形全等吗
(3)
D
(2)
A
B
C
D
E
D
E
F
(1)
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
A
B
C
D
E
F
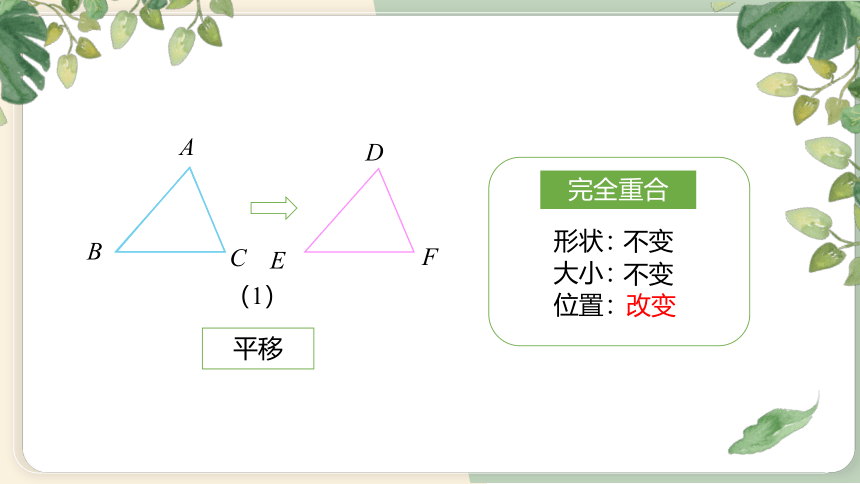
(1)
完全重合
平移
形状:
大小:
位置:
不变
不变
改变
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
翻折
D
(2)
A
B
C
完全重合
形状:
大小:
位置:
不变
不变
改变
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
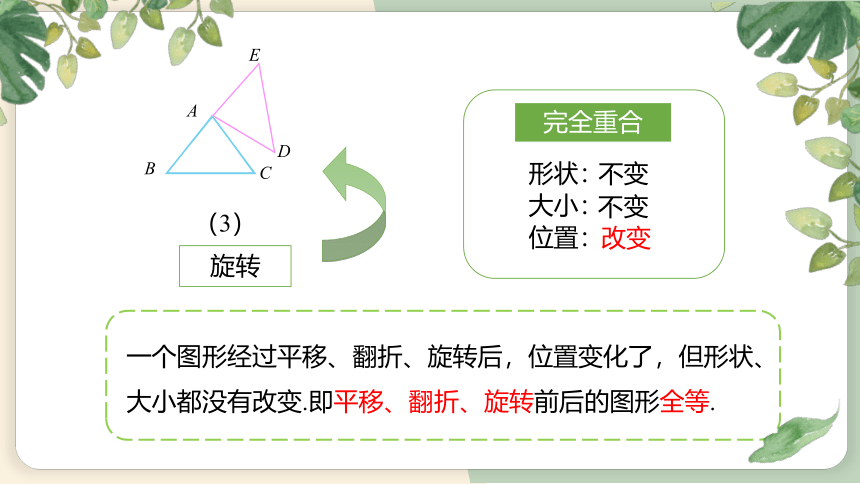
旋转
(3)
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变.即平移、翻折、旋转前后的图形全等.
完全重合
形状:
大小:
位置:
不变
不变
改变
A
B
C
D
E
B
C
A
E
F
D
观察△ABC与△DEF重合的情况.
点 A 和点 A′,点 B 和点 B′,点C 和点 C′ 互为对应顶点.
把两个全等三角形重合到一起,互相重合的顶点叫做对应顶点.
把两个全等三角形重合到一起,互相重合的角叫做对应角.
∠A 和∠A′, ∠B 和∠B′, ∠C 和∠C′ 互为对应角.
B
C
A
E
F
D
观察△ABC与△DEF重合的情况.
把两个全等三角形重合到一起,互相重合的边叫做对应边.
AB与A′B′, AC与A′C′, BC与B′C′互为对应边.
B
C
A
E
F
D
观察△ABC与△DEF重合的情况.
【总结】把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
“全等”用符号“≌”表示,读作“全等于”.
△ABC ≌ △DEF
B
C
A
E
F
D
【注意】记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
如图所示,△ABC≌△DEF 对应边有什么关系
A
B
C
D
E
F
AB=DE
BC=EF
AC=DF
全等三角形的对应边相等.
∵△ABC≌△DEF
∴AB=DE,BC=EF,AC=DF
几何语言
如图所示,△ABC≌△DEF.对应角有什么关系
A
B
C
D
E
F
∠A=∠D
∠B=∠E
∠C=∠F
全等三角形的对应角相等.
∵△ABC≌△DEF
∴∠A=∠D,∠B=∠E,∠C=∠F
几何语言
【总结】全等三角形的性质:全等三角形的对应边相等,对应角相等
D
C
A
85°
60
4
全等形:能够完全重合的两个图形叫做全等形
全等三角形:能够完全重合的两个三角形
性质:全等三角形对应边相等,对应角相等
全等三角形
小结
全等的表示方法:“全等”用符号“≌”表示,读作“全等于”.
谢谢观看
12.1全等三角形
第十二章——全等三角形
CONTENTS
了解全等形的概念;
理解并掌握全等三角形的性质.
理解并掌握全等三角形的概念和符号表示;
01
02
03
学习目标
情境导入
有人曾经说:“世界上没有两片完全相同的叶子 ”,但是在我们的日常生活中却有着许多形状、大小完全相同的图形,比如:
你能再举出一些类似的例子吗
剪刀
【探究】把手中的三角形板按在纸上,画出三角形并裁下来,裁下来的三角形纸板与三角尺放在一起形状、大小完全一样吗?能够完全重合吗?
形状、大小完全一样,能够完全重合
1.若两个图形形状、大小完全一样,能够完全重合,他们叫什么?
能够完全重合的两个图形叫做全等形.
2.两个三角形能够完全重合,又叫什么呢
能够完全重合的两个三角形叫做全等三角形.
A
B
C
A
B
C
【探究】在图(1)中,将△ABC 沿直线 BC 平移,得到△DEF.
在图(2)中,将△ABC 沿直线 BC 翻折180°,得到△DBC.
在图(3)中,将△ABC 绕点 A 旋转,得到△ADE.
各图中的两个三角形全等吗
(3)
D
(2)
A
B
C
D
E
D
E
F
(1)
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
A
B
C
D
E
F
(1)
完全重合
平移
形状:
大小:
位置:
不变
不变
改变
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
翻折
D
(2)
A
B
C
完全重合
形状:
大小:
位置:
不变
不变
改变
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
旋转
(3)
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变.即平移、翻折、旋转前后的图形全等.
完全重合
形状:
大小:
位置:
不变
不变
改变
A
B
C
D
E
B
C
A
E
F
D
观察△ABC与△DEF重合的情况.
点 A 和点 A′,点 B 和点 B′,点C 和点 C′ 互为对应顶点.
把两个全等三角形重合到一起,互相重合的顶点叫做对应顶点.
把两个全等三角形重合到一起,互相重合的角叫做对应角.
∠A 和∠A′, ∠B 和∠B′, ∠C 和∠C′ 互为对应角.
B
C
A
E
F
D
观察△ABC与△DEF重合的情况.
把两个全等三角形重合到一起,互相重合的边叫做对应边.
AB与A′B′, AC与A′C′, BC与B′C′互为对应边.
B
C
A
E
F
D
观察△ABC与△DEF重合的情况.
【总结】把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
“全等”用符号“≌”表示,读作“全等于”.
△ABC ≌ △DEF
B
C
A
E
F
D
【注意】记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
如图所示,△ABC≌△DEF 对应边有什么关系
A
B
C
D
E
F
AB=DE
BC=EF
AC=DF
全等三角形的对应边相等.
∵△ABC≌△DEF
∴AB=DE,BC=EF,AC=DF
几何语言
如图所示,△ABC≌△DEF.对应角有什么关系
A
B
C
D
E
F
∠A=∠D
∠B=∠E
∠C=∠F
全等三角形的对应角相等.
∵△ABC≌△DEF
∴∠A=∠D,∠B=∠E,∠C=∠F
几何语言
【总结】全等三角形的性质:全等三角形的对应边相等,对应角相等
D
C
A
85°
60
4
全等形:能够完全重合的两个图形叫做全等形
全等三角形:能够完全重合的两个三角形
性质:全等三角形对应边相等,对应角相等
全等三角形
小结
全等的表示方法:“全等”用符号“≌”表示,读作“全等于”.
谢谢观看
