12.2三角形全等的判定(第二课时)教学课件(共22张PPT)初中数学人教版八年级上册
文档属性
| 名称 | 12.2三角形全等的判定(第二课时)教学课件(共22张PPT)初中数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
12.2三角形全等的判定(第二课时)
第十二章——全等三角形
CONTENTS
了解利用边边角(SSA)不一定能证明三角形全等.
理解并掌握全等三角形“边角边(SAS)”的判定方法和应用;
01
02
学习目标
复习导入
上节课我们学习的“SSS”判断方法,你能说出关于它的哪些知识
B
C
A
E
F
D
三边分别相等的两个三角形全等.
(简写为“边边边”或“SSS”)
在△ABC 和△DEF中,
∴ △ABC≌△DEF(SSS)
AB = DE ,
BC = EF ,
AC = DF ,
几何语言:
复习导入
通过上节课的学习我们知道两个三角形只有一个或两个条件相等时,不能保证两个三角形全等.
给出三个条件时,有四种可能.你能说出是哪四种吗?
(1)三内角
(2)三条边
(3)两边一内角
(4)两内角一边
SSS
不能
?
?
这节课我们一起探究两边一内角相等能否判定两个三角形全等
剪刀
(1)两边及其夹角;
(2)两边及一边的对角.
两边一内角相等判定两个三角形全等存在两种情况
下面我们分别探究两种情况是否都能够判定两个三角形全等
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
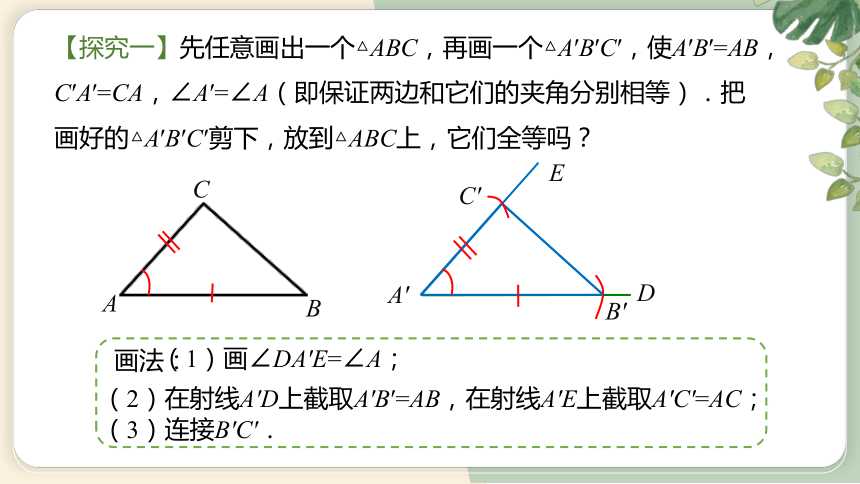
【探究一】先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,C′A′=CA,∠A′=∠A(即保证两边和它们的夹角分别相等).把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
A
B
C
A′
D
E
B′
C′
(2)在射线A′D上截取A′B′=AB,在射线A′E上截取A′C′=AC;
画法:
(3)连接B′C′.
(1)画∠DA′E=∠A;
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
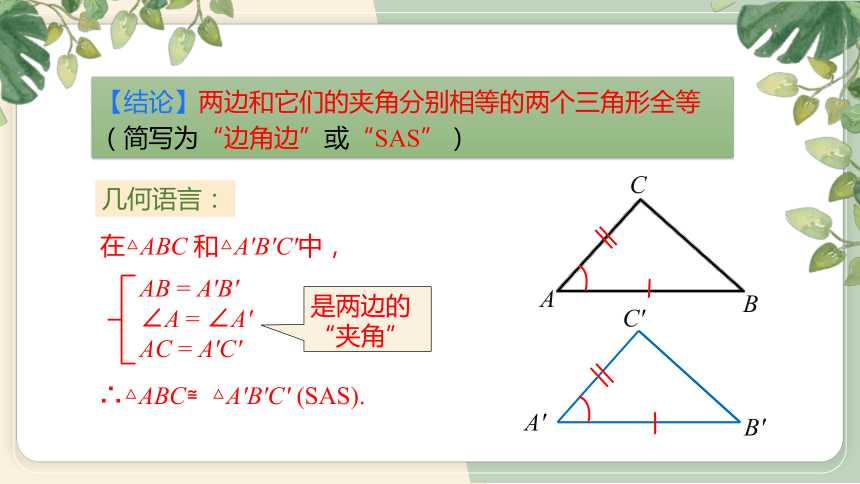
【结论】两边和它们的夹角分别相等的两个三角形全等
(简写为“边角边”或“SAS”)
几何语言:
在△ABC 和△A′B′C′中,
AB = A′B′
∠A = ∠A′
AC = A′C′
∴△ABC≌△A′B′C′ (SAS).
是两边的“夹角”
A
B
C
A′
B′
C′
例题练习
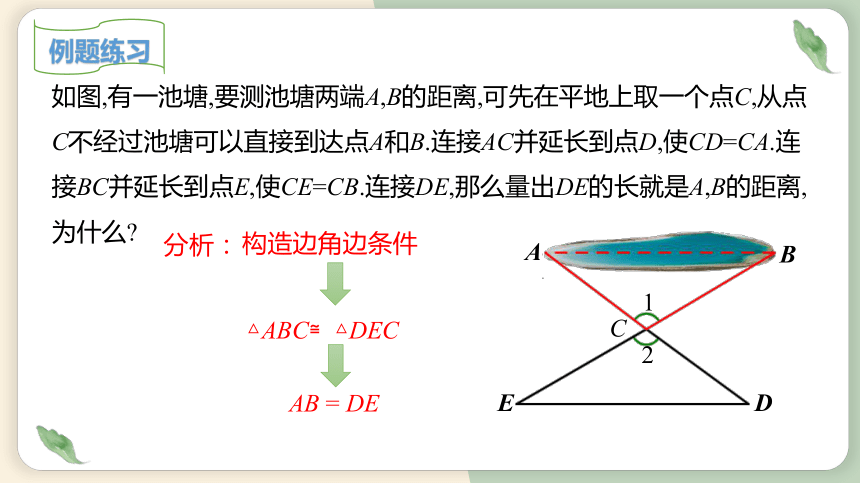
如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离,为什么
A
B
C
D
E
1
2
构造边角边条件
分析:
△ABC≌△DEC
AB = DE
例题练习
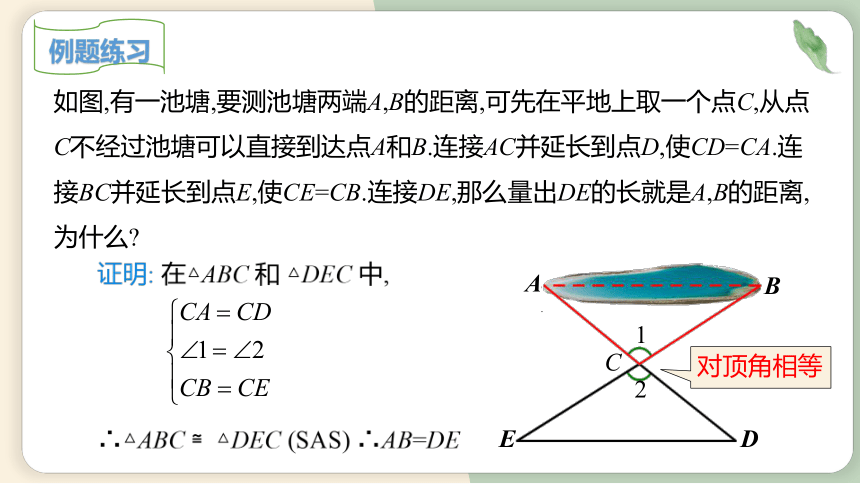
如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离,为什么
A
B
C
D
E
1
2
证明: 在△ABC 和 △DEC 中,
∴△ABC≌△DEC (SAS) ∴AB=DE
对顶角相等
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【探究二】如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC 和△ABD 满足两边和其中一边的对角分别相等,即 AB=AB ,AC=AD,∠B=∠B,但△ABC 与△ABD 不全等.
【结论】两边和其中一边的对角分别相等的两个三角形不一定全等.
1.两边和它们的夹角分别相等的两个三角形全等,简写为“边角边”或“SAS”.
2.两边和其中一边的对角分别相等的两个三角形不一定全等.
【总结】
D
C
B
边边边(SSS)
小结
判定:两边和它们的夹角分别相等的两个三角形全等(SAS).
两边和其中一边的对角分别相等的两个三角形不一定全等.
谢谢观看
12.2三角形全等的判定(第二课时)
第十二章——全等三角形
CONTENTS
了解利用边边角(SSA)不一定能证明三角形全等.
理解并掌握全等三角形“边角边(SAS)”的判定方法和应用;
01
02
学习目标
复习导入
上节课我们学习的“SSS”判断方法,你能说出关于它的哪些知识
B
C
A
E
F
D
三边分别相等的两个三角形全等.
(简写为“边边边”或“SSS”)
在△ABC 和△DEF中,
∴ △ABC≌△DEF(SSS)
AB = DE ,
BC = EF ,
AC = DF ,
几何语言:
复习导入
通过上节课的学习我们知道两个三角形只有一个或两个条件相等时,不能保证两个三角形全等.
给出三个条件时,有四种可能.你能说出是哪四种吗?
(1)三内角
(2)三条边
(3)两边一内角
(4)两内角一边
SSS
不能
?
?
这节课我们一起探究两边一内角相等能否判定两个三角形全等
剪刀
(1)两边及其夹角;
(2)两边及一边的对角.
两边一内角相等判定两个三角形全等存在两种情况
下面我们分别探究两种情况是否都能够判定两个三角形全等
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【探究一】先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,C′A′=CA,∠A′=∠A(即保证两边和它们的夹角分别相等).把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
A
B
C
A′
D
E
B′
C′
(2)在射线A′D上截取A′B′=AB,在射线A′E上截取A′C′=AC;
画法:
(3)连接B′C′.
(1)画∠DA′E=∠A;
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【结论】两边和它们的夹角分别相等的两个三角形全等
(简写为“边角边”或“SAS”)
几何语言:
在△ABC 和△A′B′C′中,
AB = A′B′
∠A = ∠A′
AC = A′C′
∴△ABC≌△A′B′C′ (SAS).
是两边的“夹角”
A
B
C
A′
B′
C′
例题练习
如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离,为什么
A
B
C
D
E
1
2
构造边角边条件
分析:
△ABC≌△DEC
AB = DE
例题练习
如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离,为什么
A
B
C
D
E
1
2
证明: 在△ABC 和 △DEC 中,
∴△ABC≌△DEC (SAS) ∴AB=DE
对顶角相等
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【探究二】如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC 和△ABD 满足两边和其中一边的对角分别相等,即 AB=AB ,AC=AD,∠B=∠B,但△ABC 与△ABD 不全等.
【结论】两边和其中一边的对角分别相等的两个三角形不一定全等.
1.两边和它们的夹角分别相等的两个三角形全等,简写为“边角边”或“SAS”.
2.两边和其中一边的对角分别相等的两个三角形不一定全等.
【总结】
D
C
B
边边边(SSS)
小结
判定:两边和它们的夹角分别相等的两个三角形全等(SAS).
两边和其中一边的对角分别相等的两个三角形不一定全等.
谢谢观看
