12.2三角形全等的判定(第三课时)教学课件(共23张PPT)初中数学人教版八年级上册
文档属性
| 名称 | 12.2三角形全等的判定(第三课时)教学课件(共23张PPT)初中数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
12.2三角形全等的判定(第三课时)
第十二章——全等三角形
COTENTS
理解并掌握全等三角形“角角边(AAS)”的判定方法和应用.
理解并掌握全等三角形“角边角(ASA)”的判定方法和应用;
01
02
学习目标
回顾旧知
目前我们已经学习了证明三角形全等的两种判定方法,分别是“边边边(SSS)”和边角边(SAS),回顾一下关于这两种判定方法的具体内容
B
C
A
E
F
D
三边分别相等的两个三角形全等(简写为“边边边”或“SSS”)
在△ABC 和△DEF中,
∴ △ABC≌△DEF(SSS)
AB = DE ,
BC = EF ,
AC = DF ,
几何语言:
回顾旧知
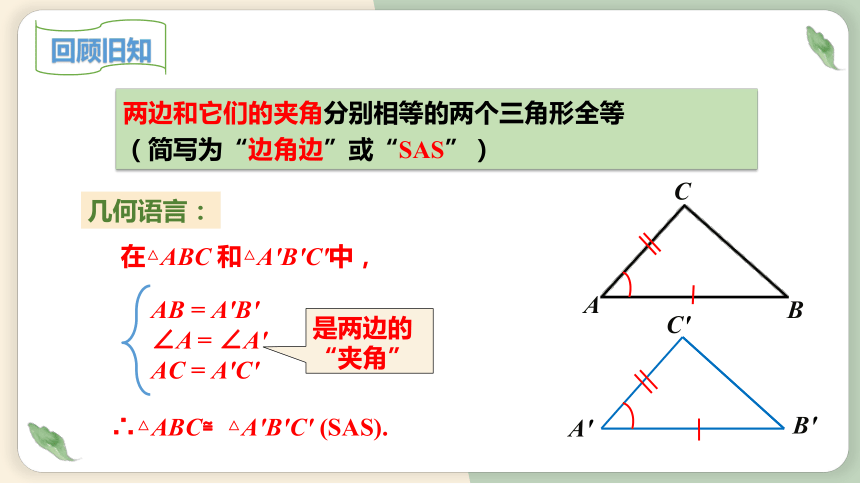
两边和它们的夹角分别相等的两个三角形全等
(简写为“边角边”或“SAS”)
几何语言:
在△ABC 和△A′B′C′中,
AB = A′B′
∠A = ∠A′
AC = A′C′
∴△ABC≌△A′B′C′ (SAS).
是两边的“夹角”
A
B
C
A′
C′
B′
复习导入
给出三个条件证明两个三角形全等时,有四种可能,分别是
(1)三内角
(2)三条边
(3)两边一内角
(4)两内角一边
SSS
不能
SAS
?
这节课我们一起探究两内角一边相等能否判定两个三角形全等
剪刀
(1)两角及夹边;
(2)两角和其中一角的对边.
两内角一边相等判定两个三角形全等存在两种情况
下面我们分别探究两种情况是否都能够判定两个三角形全等
【探究一】先任意画出一个△ABC,再画出一个△A′B′C′ , 使A′B′=AB, ∠A′=∠A, ∠B′ =∠B (即两角和它们的夹边分别相等).把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
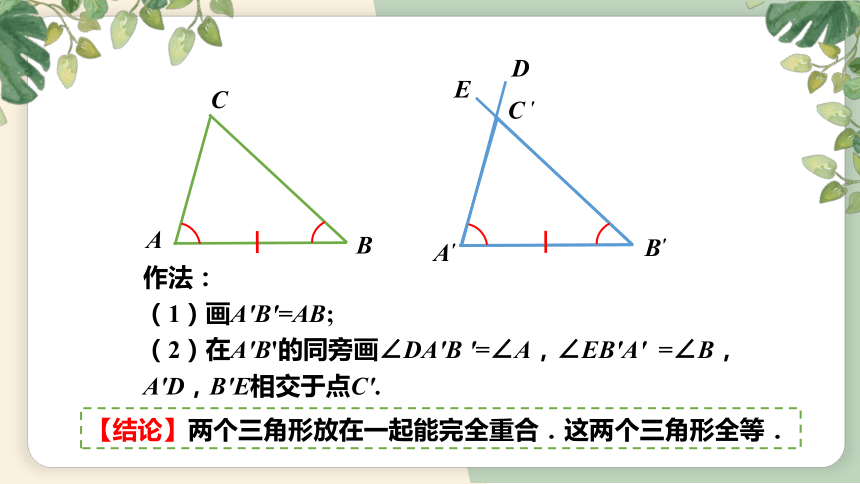
作法:
(1)画A'B'=AB;
(2)在A'B'的同旁画∠DA'B '=∠A,∠EB'A' =∠B,A'D,B'E相交于点C'.
【结论】两个三角形放在一起能完全重合.这两个三角形全等.
A
C
B
A′
B′
C ′
E
D
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
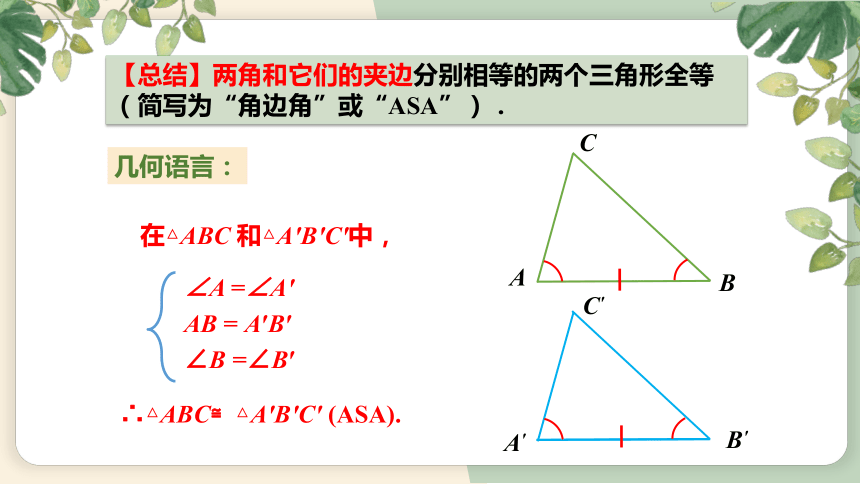
【总结】两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
几何语言:
在△ABC 和△A′B′C′中,
∴△ABC≌△A′B′C′ (ASA).
A
C
B
A′
B′
C′
∠A =∠A′
AB = A′B′
∠B =∠B′
例题练习
如图为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是只带第③块碎片.其理论依据是( )
①
②
③
A
例题练习
如图,点 D 在 AB 上,点 E 在 AC上,AB=AC,∠B =∠C.
求证 AD =AE.
分析:证明△ACD≌△ABE,就可以得出AD=AE.
证明:在△ACD和△ABE中,
∠A = ∠A(公共角)
AC = AB
∠C = ∠B
∴ △ACD≌△ABE(ASA),
∴AD=AE.
例题练习
如图,在△ABC 和△DEF 中,∠A =∠D,∠B =∠E,BC =EF . 求证△ABC ≌△DEF.
A
B
C
F
E
D
分析:
△ABC ≌△DEF(ASA)
证明∠C=∠F
三角形内角和定理
例题练习
A
B
C
F
E
D
∠B=∠E
BC=EF
∠C=∠F
证明:
在△ABC 中,∠A+∠B+∠C=180°.
∴△ABC≌△DEF(ASA ).
∴ ∠C=180°-∠A-∠B.
同理 ∠F=180°-∠D-∠E.
又 ∠A=∠D,∠B= ∠E,
∴ ∠C=∠F.
在△ABC 和△DEF 中,
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【总结】两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.
几何语言:
在△ABC 和△A′B′C′中,
∴△ABC≌△A′B′C′ (AAS).
A
C
B
A′
B′
C ′
∠A = ∠A′
∠B = ∠B′
AC = A′C ′
1.两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
2.两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS ”.
【总结】
D
C
∠B=∠E
角边角(ASA)角角边(AAS)
小结
两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.
谢谢观看
12.2三角形全等的判定(第三课时)
第十二章——全等三角形
COTENTS
理解并掌握全等三角形“角角边(AAS)”的判定方法和应用.
理解并掌握全等三角形“角边角(ASA)”的判定方法和应用;
01
02
学习目标
回顾旧知
目前我们已经学习了证明三角形全等的两种判定方法,分别是“边边边(SSS)”和边角边(SAS),回顾一下关于这两种判定方法的具体内容
B
C
A
E
F
D
三边分别相等的两个三角形全等(简写为“边边边”或“SSS”)
在△ABC 和△DEF中,
∴ △ABC≌△DEF(SSS)
AB = DE ,
BC = EF ,
AC = DF ,
几何语言:
回顾旧知
两边和它们的夹角分别相等的两个三角形全等
(简写为“边角边”或“SAS”)
几何语言:
在△ABC 和△A′B′C′中,
AB = A′B′
∠A = ∠A′
AC = A′C′
∴△ABC≌△A′B′C′ (SAS).
是两边的“夹角”
A
B
C
A′
C′
B′
复习导入
给出三个条件证明两个三角形全等时,有四种可能,分别是
(1)三内角
(2)三条边
(3)两边一内角
(4)两内角一边
SSS
不能
SAS
?
这节课我们一起探究两内角一边相等能否判定两个三角形全等
剪刀
(1)两角及夹边;
(2)两角和其中一角的对边.
两内角一边相等判定两个三角形全等存在两种情况
下面我们分别探究两种情况是否都能够判定两个三角形全等
【探究一】先任意画出一个△ABC,再画出一个△A′B′C′ , 使A′B′=AB, ∠A′=∠A, ∠B′ =∠B (即两角和它们的夹边分别相等).把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
作法:
(1)画A'B'=AB;
(2)在A'B'的同旁画∠DA'B '=∠A,∠EB'A' =∠B,A'D,B'E相交于点C'.
【结论】两个三角形放在一起能完全重合.这两个三角形全等.
A
C
B
A′
B′
C ′
E
D
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【总结】两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
几何语言:
在△ABC 和△A′B′C′中,
∴△ABC≌△A′B′C′ (ASA).
A
C
B
A′
B′
C′
∠A =∠A′
AB = A′B′
∠B =∠B′
例题练习
如图为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是只带第③块碎片.其理论依据是( )
①
②
③
A
例题练习
如图,点 D 在 AB 上,点 E 在 AC上,AB=AC,∠B =∠C.
求证 AD =AE.
分析:证明△ACD≌△ABE,就可以得出AD=AE.
证明:在△ACD和△ABE中,
∠A = ∠A(公共角)
AC = AB
∠C = ∠B
∴ △ACD≌△ABE(ASA),
∴AD=AE.
例题练习
如图,在△ABC 和△DEF 中,∠A =∠D,∠B =∠E,BC =EF . 求证△ABC ≌△DEF.
A
B
C
F
E
D
分析:
△ABC ≌△DEF(ASA)
证明∠C=∠F
三角形内角和定理
例题练习
A
B
C
F
E
D
∠B=∠E
BC=EF
∠C=∠F
证明:
在△ABC 中,∠A+∠B+∠C=180°.
∴△ABC≌△DEF(ASA ).
∴ ∠C=180°-∠A-∠B.
同理 ∠F=180°-∠D-∠E.
又 ∠A=∠D,∠B= ∠E,
∴ ∠C=∠F.
在△ABC 和△DEF 中,
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【总结】两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.
几何语言:
在△ABC 和△A′B′C′中,
∴△ABC≌△A′B′C′ (AAS).
A
C
B
A′
B′
C ′
∠A = ∠A′
∠B = ∠B′
AC = A′C ′
1.两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
2.两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS ”.
【总结】
D
C
∠B=∠E
角边角(ASA)角角边(AAS)
小结
两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.
谢谢观看
