13.1.2线段的垂直平分线的性质 课件(共29张PPT) 初中数学人教版八年级上册
文档属性
| 名称 | 13.1.2线段的垂直平分线的性质 课件(共29张PPT) 初中数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 21.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 20:54:54 | ||
图片预览






文档简介
(共28张PPT)
13.1.2线段的垂直平分线的性质
第十三章——轴对称
COTENTS
能用尺规作图过一点作已知直线的垂线;
理解并掌握线段垂直平分线的性质及判定;
01
02
学习目标
能作出轴对称图形的对称轴,即线段垂直平分线的尺规作图.
03
知识回顾
上节课我们学习了线段垂直平分线的概念,什么叫线段垂直平分线?
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.也把这条直线叫做中垂线.
N
M
P
如图,MN⊥AA′,垂足为P,
且 AP = A′P,则称直线MN是线段AA′ 的垂直平分线.
A′
A
探究新知
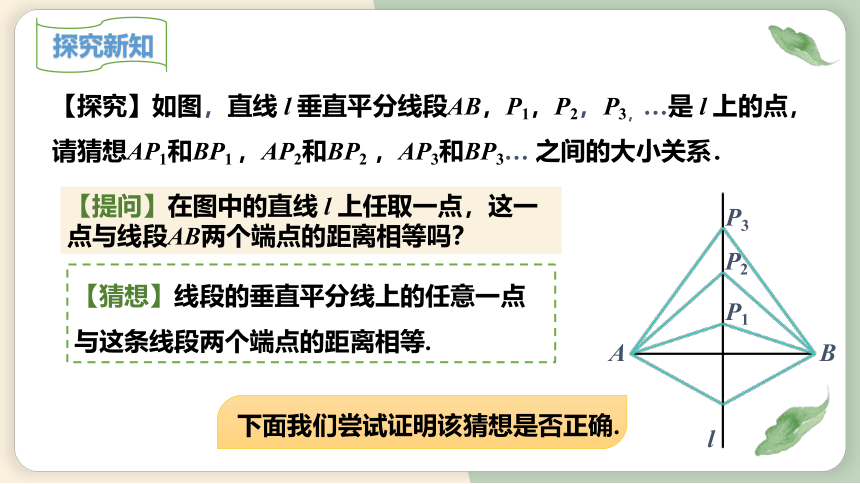
【探究】如图,直线 l 垂直平分线段AB,P1,P2,P3,…是 l 上的点,请猜想AP1和BP1 ,AP2和BP2 ,AP3和BP3… 之间的大小关系.
A
B
l
P1
P2
P3
AP1=BP1 ,AP2=BP2 ,AP3 =BP3 …
探究新知
A
B
l
P1
P2
P3
【猜想】线段的垂直平分线上的任意一点与这条线段两个端点的距离相等.
【提问】在图中的直线 l 上任取一点,这一点与线段AB两个端点的距离相等吗?
下面我们尝试证明该猜想是否正确.
【探究】如图,直线 l 垂直平分线段AB,P1,P2,P3,…是 l 上的点,请猜想AP1和BP1 ,AP2和BP2 ,AP3和BP3… 之间的大小关系.
A
B
l
┐
C
P
已知:如图,直线 l⊥AB,垂足为C,AC =CB,点
P 在 l 上.求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB = 90°.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
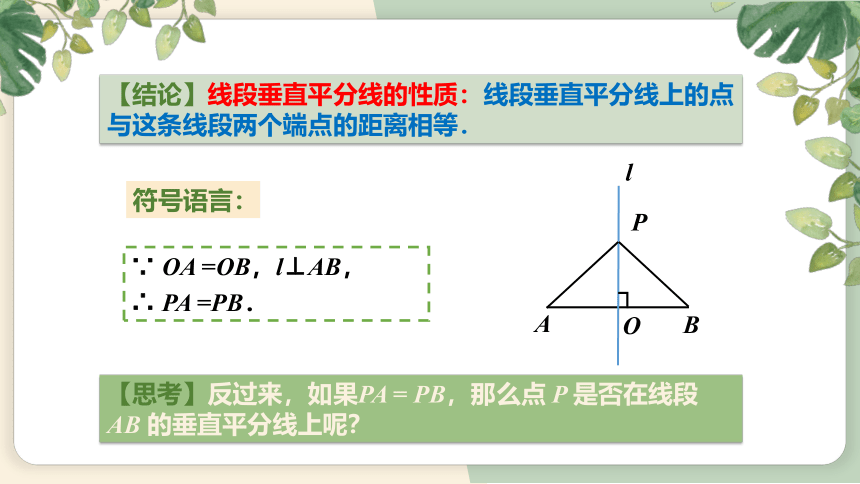
【结论】线段垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.
符号语言:
∵ OA =OB,l⊥AB,
∴ PA =PB.
A
B
l
┐
O
P
【思考】反过来,如果PA = PB,那么点 P 是否在线段 AB 的垂直平分线上呢?
【猜想】与一条线段两个端点距离相等的点在这条线段的垂直平分线上,即如果 PA=PB,则点P在线段AB的垂直平分线上.
已知:如图,PA =PB.求证:点P在线段AB 的垂直平分线上.
证明:如图作PC⊥AB
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌ Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上
A
B
P
┐
C
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
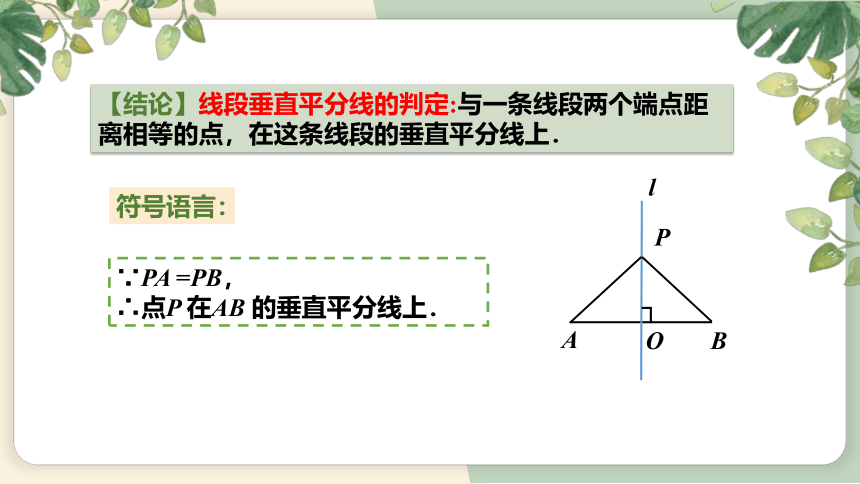
【结论】线段垂直平分线的判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
符号语言:
∵PA =PB,
∴点P 在AB 的垂直平分线上.
A
B
l
┐
O
P
1、从上面两个结论可以看出,在线段AB的垂直平分线l上的点与点A,B的距离都相等.
2、反过来,与A,B的距离相等的点都在l上,所以直线 l 可以看成与两点A,B的距离相等的所有点的集合.
A
B
l
┐
O
P
例题练习
尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线AB和AB外一点C.求作:AB的垂线,使它经过点C.
作法:(1)任意取一点K,使点K 和点C 在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E.
(3)分别以点D和E为圆心,以大于DE一半的长为半径作弧,两弧相交于点F.
(4)作直线CF.直线CF 就是所求的垂线.
为什么直线CF 就是所求作的垂线?
K
A
B
C
D
E
F
剪刀
从作法的(2)(3)步可知CD=CE,DF=EF,
∴点C,F 都在DE的垂直平分线上.
∴CF 就是线段DE的垂直平分线.
又∵点D,E 在直线 AB 上,
∴CF 就是所求直线 AB 的垂线.
【思考】为什么直线CF 就是所求作的垂线?
A
B
C
D
E
F
剪刀
【思考】有时我们感觉两个平面图形是成轴对称的,但是如何验证呢?在不折叠图形的情况下,你能准确地做出轴对称图形的对称轴吗?
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.因此,只要能找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
【分析】我们只要连接点A和点B,作出线段AB的垂直平分线,就可以得到点A和点B的对称轴,为此作出到点A、B距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
A
B
作法:如图所示:
(1)分别以点A和点B为圆心,大于 AB的长为半径作弧(想一想为什么),两弧线相交于C,D两点;
(2)作直线CD,即是所求作的直线.
A
B
C
D
这种作法的依据是什么?
这种作图方法还有哪些作用?
线段垂直平分线的尺规作图
如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
确定线段的中点
作对称轴的步骤:
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:做出对应点所连线段的垂直平分线.
找对应点时,一般找图形的顶点或转折点,这样做出的图形更准确.
例题练习
如图中的五角星,请作出它的一条对称轴.
A
A′
l
可以选择一对对应点A和A′,连接AA′,作出线段AA′的垂直平分线 l,则 l 就是这个五角星的一条对称轴.
类似地,请你尝试作出这个五角星的其他对称轴.
A
C
线段的垂直平分线
小结
性质:线段垂直平分线上的点与这条线段
两个端点的距离相等
判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
谢谢观看
13.1.2线段的垂直平分线的性质
第十三章——轴对称
COTENTS
能用尺规作图过一点作已知直线的垂线;
理解并掌握线段垂直平分线的性质及判定;
01
02
学习目标
能作出轴对称图形的对称轴,即线段垂直平分线的尺规作图.
03
知识回顾
上节课我们学习了线段垂直平分线的概念,什么叫线段垂直平分线?
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.也把这条直线叫做中垂线.
N
M
P
如图,MN⊥AA′,垂足为P,
且 AP = A′P,则称直线MN是线段AA′ 的垂直平分线.
A′
A
探究新知
【探究】如图,直线 l 垂直平分线段AB,P1,P2,P3,…是 l 上的点,请猜想AP1和BP1 ,AP2和BP2 ,AP3和BP3… 之间的大小关系.
A
B
l
P1
P2
P3
AP1=BP1 ,AP2=BP2 ,AP3 =BP3 …
探究新知
A
B
l
P1
P2
P3
【猜想】线段的垂直平分线上的任意一点与这条线段两个端点的距离相等.
【提问】在图中的直线 l 上任取一点,这一点与线段AB两个端点的距离相等吗?
下面我们尝试证明该猜想是否正确.
【探究】如图,直线 l 垂直平分线段AB,P1,P2,P3,…是 l 上的点,请猜想AP1和BP1 ,AP2和BP2 ,AP3和BP3… 之间的大小关系.
A
B
l
┐
C
P
已知:如图,直线 l⊥AB,垂足为C,AC =CB,点
P 在 l 上.求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB = 90°.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【结论】线段垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.
符号语言:
∵ OA =OB,l⊥AB,
∴ PA =PB.
A
B
l
┐
O
P
【思考】反过来,如果PA = PB,那么点 P 是否在线段 AB 的垂直平分线上呢?
【猜想】与一条线段两个端点距离相等的点在这条线段的垂直平分线上,即如果 PA=PB,则点P在线段AB的垂直平分线上.
已知:如图,PA =PB.求证:点P在线段AB 的垂直平分线上.
证明:如图作PC⊥AB
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌ Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上
A
B
P
┐
C
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【结论】线段垂直平分线的判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
符号语言:
∵PA =PB,
∴点P 在AB 的垂直平分线上.
A
B
l
┐
O
P
1、从上面两个结论可以看出,在线段AB的垂直平分线l上的点与点A,B的距离都相等.
2、反过来,与A,B的距离相等的点都在l上,所以直线 l 可以看成与两点A,B的距离相等的所有点的集合.
A
B
l
┐
O
P
例题练习
尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线AB和AB外一点C.求作:AB的垂线,使它经过点C.
作法:(1)任意取一点K,使点K 和点C 在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E.
(3)分别以点D和E为圆心,以大于DE一半的长为半径作弧,两弧相交于点F.
(4)作直线CF.直线CF 就是所求的垂线.
为什么直线CF 就是所求作的垂线?
K
A
B
C
D
E
F
剪刀
从作法的(2)(3)步可知CD=CE,DF=EF,
∴点C,F 都在DE的垂直平分线上.
∴CF 就是线段DE的垂直平分线.
又∵点D,E 在直线 AB 上,
∴CF 就是所求直线 AB 的垂线.
【思考】为什么直线CF 就是所求作的垂线?
A
B
C
D
E
F
剪刀
【思考】有时我们感觉两个平面图形是成轴对称的,但是如何验证呢?在不折叠图形的情况下,你能准确地做出轴对称图形的对称轴吗?
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.因此,只要能找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
【分析】我们只要连接点A和点B,作出线段AB的垂直平分线,就可以得到点A和点B的对称轴,为此作出到点A、B距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
A
B
作法:如图所示:
(1)分别以点A和点B为圆心,大于 AB的长为半径作弧(想一想为什么),两弧线相交于C,D两点;
(2)作直线CD,即是所求作的直线.
A
B
C
D
这种作法的依据是什么?
这种作图方法还有哪些作用?
线段垂直平分线的尺规作图
如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
确定线段的中点
作对称轴的步骤:
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:做出对应点所连线段的垂直平分线.
找对应点时,一般找图形的顶点或转折点,这样做出的图形更准确.
例题练习
如图中的五角星,请作出它的一条对称轴.
A
A′
l
可以选择一对对应点A和A′,连接AA′,作出线段AA′的垂直平分线 l,则 l 就是这个五角星的一条对称轴.
类似地,请你尝试作出这个五角星的其他对称轴.
A
C
线段的垂直平分线
小结
性质:线段垂直平分线上的点与这条线段
两个端点的距离相等
判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
谢谢观看
