13.3.2等边三角形 课件(共29张PPT) 初中数学人教版八年级上册
文档属性
| 名称 | 13.3.2等边三角形 课件(共29张PPT) 初中数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 17.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 00:00:00 | ||
图片预览



文档简介
(共29张PPT)
13.3.2等边三角形
第十三章——轴对称
探索等边三角形的轴对称性;
理解并掌握等边三角形的性质和判定方法;
01
02
学习目标
理解并掌握有一个角是30°的直角三角形的性质
03
知识回顾
上节课我们学习了等腰三角形,回顾一下关于等腰三角形的知识.
名称 图形 定义 性质 判定
等腰三角形 有两条边相等的三角形叫做等腰三角形 两腰相等 两边相等
等边对等角 等角对等边
三线合一
轴对称图形
引入新知
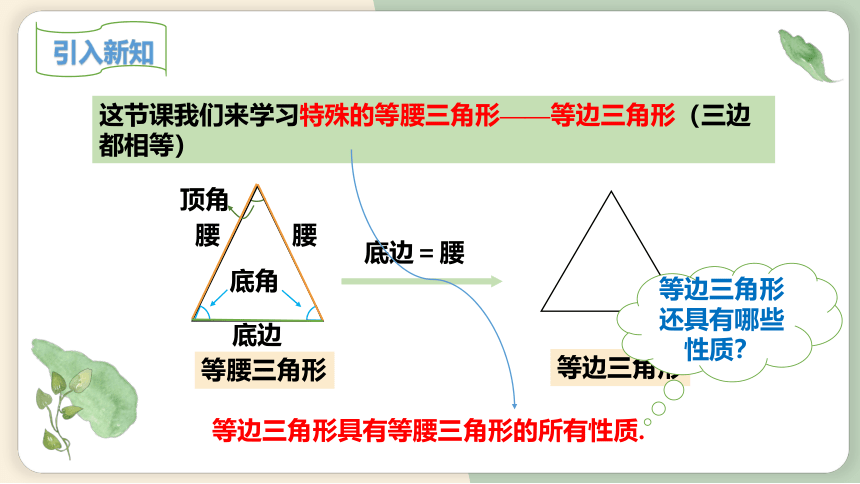
这节课我们来学习特殊的等腰三角形——等边三角形(三边都相等)
等腰三角形
等边三角形
腰
腰
底边
底角
顶角
底边=腰
等边三角形具有等腰三角形的所有性质.
等边三角形还具有哪些性质?
【探究1】把等腰三角形的性质用于等边三角形,能得到等边三角形的什么性质?
等腰三角形的性质1:等腰三角形的两个底角相等.
等边三角形的三个内角都相等,并且每一个角都等于60°.
A
B
C
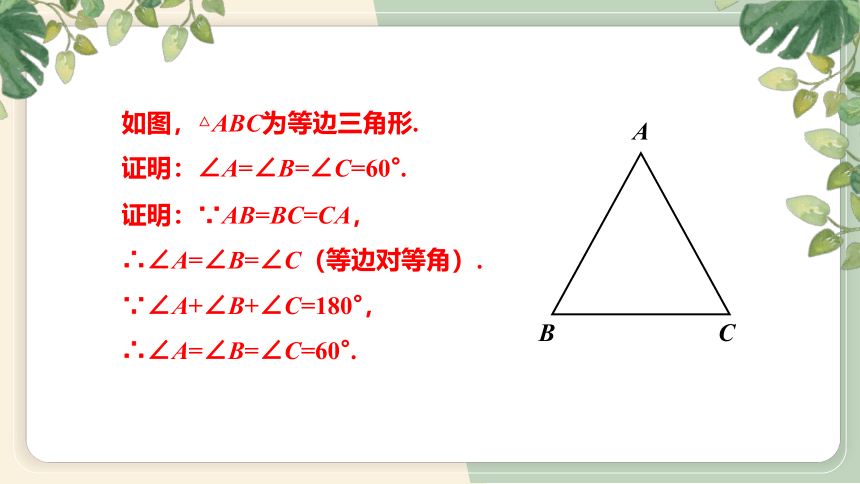
证明:∵AB=BC=CA,
∴∠A=∠B=∠C(等边对等角).
∵∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°.
如图,△ABC为等边三角形.
证明:∠A=∠B=∠C=60°.
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
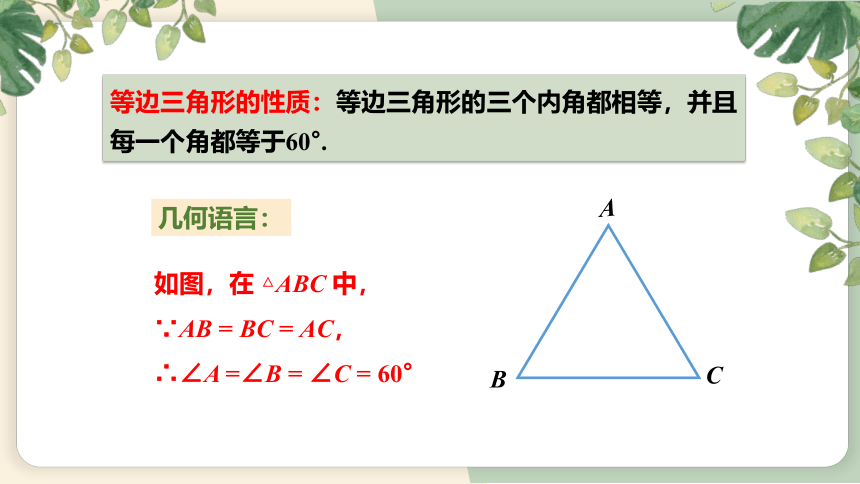
等边三角形的性质:等边三角形的三个内角都相等,并且每一个角都等于60°.
几何语言:
A
B
C
如图,在 △ABC 中,
∵AB = BC = AC,
∴∠A =∠B = ∠C = 60°
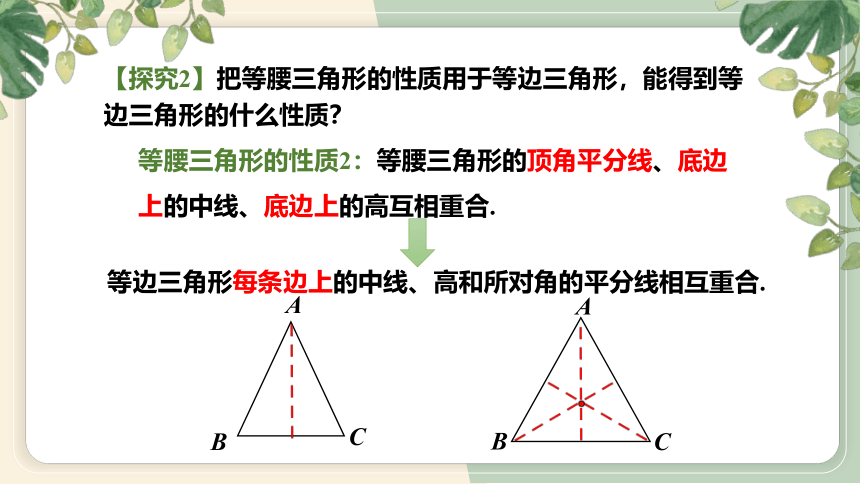
【探究2】把等腰三角形的性质用于等边三角形,能得到等边三角形的什么性质?
等边三角形每条边上的中线、高和所对角的平分线相互重合.
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
A
B
C
A
B
C
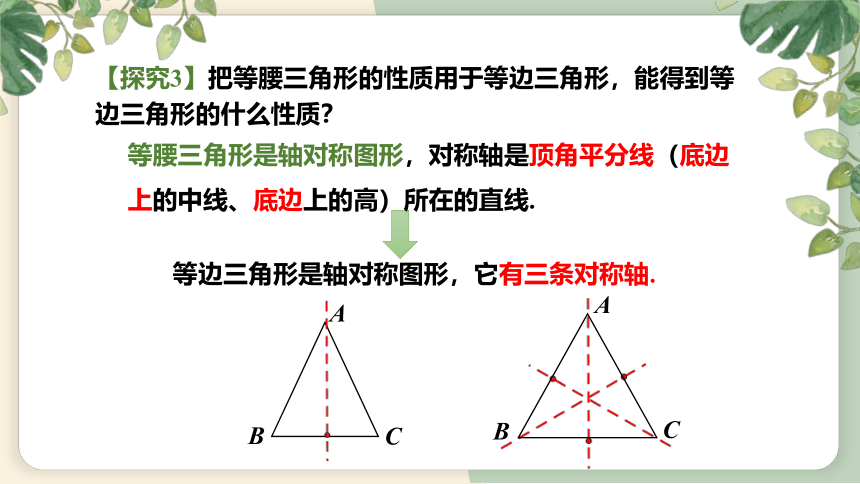
【探究3】把等腰三角形的性质用于等边三角形,能得到等边三角形的什么性质?
等边三角形是轴对称图形,它有三条对称轴.
等腰三角形是轴对称图形,对称轴是顶角平分线(底边上的中线、底边上的高)所在的直线.
A
B
C
A
B
C
图形 等腰三角形 等边三角形
性质 边
角
三线合一
对称性
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,且都是 60°
3 条对称轴
1 条对称轴
两个底角相等
底边上的中线、高和顶角的平分线互相重合
两条边相等
三条边都相等
总结
【探究4】类比等腰三角形的判定,一个三角形的三个内角满足什么条件才是等边三角形?
图形 等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
【思考】等边三角形还有其他的判定方法吗?
有一个角是60°的等腰三角形是等边三角形
【总结】等边三角形的判定方法:
3. 有一个角是______的等腰三角形是等边三角形.
2. 三个角都______的三角形是等边三角形;
1. 三边都______的三角形是等边三角形;
相等
相等
60°
例题练习
如图,在等边三角形 ABC 中,DE∥BC.
求证:△ADE 是等边三角形.
A
C
B
D
E
证明:
∵△ABC 是等边三角形,
∴∠A =∠B =∠C.
∵ DE∥BC,
∴∠ADE =∠B,∠AED =∠C.
∴∠A =∠ADE =∠AED.
∴△ADE 是等边三角形.
本题还有其他证法吗?
若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然成立吗?
证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C
∵ DE∥BC,∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.
A
D
E
B
C
【探究5】如图,将两个相同的含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
A
C
B
∵△ABC 是 △ADC 的轴对称图形
∴AB=AD
又∵∠B=60°
∴ △ABD 是等边三角形
又∵AC⊥BD
∴BC=DC= AB
A
C
B
D
在直角三角形中,如果一个锐角等于30°,那么,它所对的直角边等于斜边的一半.
你还有其他方法证明该结论吗?
E
A
B
C
证明: 在BA上截取 BE=BC,连接 EC.
∵ ∠B= 60° ,BE = BC. ∴ △BCE是等边三角形,
∴ ∠BEC= 60°,BE=EC.
∵ ∠A= 30°,
∴ ∠ECA=∠BEC-∠A=60°-30° = 30°.
∴ AE=EC,
∴ AE=BE=BC,
∴ AB=AE+BE=2BC,
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°,
求证:BC = AB.
∴BC = AB.
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
含30°角的直角三角形的性质 :在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言:
∵ 在Rt△ABC 中,∠C =90°,∠A =30°,
∴ BC = AB.
A
B
C
例题练习
如图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4 m,∠A = 30°,立柱 BC,DE 的长是多少?
A
B
C
D
E
分析:
BC
Rt△ACB
DE
Rt△AED
例题练习
如图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4 m,∠A = 30°,立柱 BC,DE 的长是多少?
A
B
C
D
E
解:∵DE⊥AC,BC⊥AC,∠A=30°,
答:立柱BC的长是3.7m,DE的长是1.85m
∴
∴ 7.4=3.7(m)
又AD=,
∴DE== 3.7=1.85(m)
C
50
3
4
小结
1. __________的三角形等边三角形
3.____________的三角形是等边三角形
2.等边三角形的三个内角______ ,并且每一个内角________
三个角都相等
都相等
4.有____个角是___的______三角形是等边三角形
一
60°
等腰
三边都相等
等于 60°
5.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的 .
一半
谢谢观看
13.3.2等边三角形
第十三章——轴对称
探索等边三角形的轴对称性;
理解并掌握等边三角形的性质和判定方法;
01
02
学习目标
理解并掌握有一个角是30°的直角三角形的性质
03
知识回顾
上节课我们学习了等腰三角形,回顾一下关于等腰三角形的知识.
名称 图形 定义 性质 判定
等腰三角形 有两条边相等的三角形叫做等腰三角形 两腰相等 两边相等
等边对等角 等角对等边
三线合一
轴对称图形
引入新知
这节课我们来学习特殊的等腰三角形——等边三角形(三边都相等)
等腰三角形
等边三角形
腰
腰
底边
底角
顶角
底边=腰
等边三角形具有等腰三角形的所有性质.
等边三角形还具有哪些性质?
【探究1】把等腰三角形的性质用于等边三角形,能得到等边三角形的什么性质?
等腰三角形的性质1:等腰三角形的两个底角相等.
等边三角形的三个内角都相等,并且每一个角都等于60°.
A
B
C
证明:∵AB=BC=CA,
∴∠A=∠B=∠C(等边对等角).
∵∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°.
如图,△ABC为等边三角形.
证明:∠A=∠B=∠C=60°.
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
等边三角形的性质:等边三角形的三个内角都相等,并且每一个角都等于60°.
几何语言:
A
B
C
如图,在 △ABC 中,
∵AB = BC = AC,
∴∠A =∠B = ∠C = 60°
【探究2】把等腰三角形的性质用于等边三角形,能得到等边三角形的什么性质?
等边三角形每条边上的中线、高和所对角的平分线相互重合.
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
A
B
C
A
B
C
【探究3】把等腰三角形的性质用于等边三角形,能得到等边三角形的什么性质?
等边三角形是轴对称图形,它有三条对称轴.
等腰三角形是轴对称图形,对称轴是顶角平分线(底边上的中线、底边上的高)所在的直线.
A
B
C
A
B
C
图形 等腰三角形 等边三角形
性质 边
角
三线合一
对称性
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,且都是 60°
3 条对称轴
1 条对称轴
两个底角相等
底边上的中线、高和顶角的平分线互相重合
两条边相等
三条边都相等
总结
【探究4】类比等腰三角形的判定,一个三角形的三个内角满足什么条件才是等边三角形?
图形 等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
【思考】等边三角形还有其他的判定方法吗?
有一个角是60°的等腰三角形是等边三角形
【总结】等边三角形的判定方法:
3. 有一个角是______的等腰三角形是等边三角形.
2. 三个角都______的三角形是等边三角形;
1. 三边都______的三角形是等边三角形;
相等
相等
60°
例题练习
如图,在等边三角形 ABC 中,DE∥BC.
求证:△ADE 是等边三角形.
A
C
B
D
E
证明:
∵△ABC 是等边三角形,
∴∠A =∠B =∠C.
∵ DE∥BC,
∴∠ADE =∠B,∠AED =∠C.
∴∠A =∠ADE =∠AED.
∴△ADE 是等边三角形.
本题还有其他证法吗?
若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然成立吗?
证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C
∵ DE∥BC,∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.
A
D
E
B
C
【探究5】如图,将两个相同的含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
A
C
B
∵△ABC 是 △ADC 的轴对称图形
∴AB=AD
又∵∠B=60°
∴ △ABD 是等边三角形
又∵AC⊥BD
∴BC=DC= AB
A
C
B
D
在直角三角形中,如果一个锐角等于30°,那么,它所对的直角边等于斜边的一半.
你还有其他方法证明该结论吗?
E
A
B
C
证明: 在BA上截取 BE=BC,连接 EC.
∵ ∠B= 60° ,BE = BC. ∴ △BCE是等边三角形,
∴ ∠BEC= 60°,BE=EC.
∵ ∠A= 30°,
∴ ∠ECA=∠BEC-∠A=60°-30° = 30°.
∴ AE=EC,
∴ AE=BE=BC,
∴ AB=AE+BE=2BC,
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°,
求证:BC = AB.
∴BC = AB.
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
含30°角的直角三角形的性质 :在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言:
∵ 在Rt△ABC 中,∠C =90°,∠A =30°,
∴ BC = AB.
A
B
C
例题练习
如图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4 m,∠A = 30°,立柱 BC,DE 的长是多少?
A
B
C
D
E
分析:
BC
Rt△ACB
DE
Rt△AED
例题练习
如图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4 m,∠A = 30°,立柱 BC,DE 的长是多少?
A
B
C
D
E
解:∵DE⊥AC,BC⊥AC,∠A=30°,
答:立柱BC的长是3.7m,DE的长是1.85m
∴
∴ 7.4=3.7(m)
又AD=,
∴DE== 3.7=1.85(m)
C
50
3
4
小结
1. __________的三角形等边三角形
3.____________的三角形是等边三角形
2.等边三角形的三个内角______ ,并且每一个内角________
三个角都相等
都相等
4.有____个角是___的______三角形是等边三角形
一
60°
等腰
三边都相等
等于 60°
5.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的 .
一半
谢谢观看
