13.3.1等腰三角形 课件(共35张PPT) 初中数学人教版八年级上册
文档属性
| 名称 | 13.3.1等腰三角形 课件(共35张PPT) 初中数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 00:00:00 | ||
图片预览


文档简介
(共35张PPT)
13.3.1等腰三角形
第十三章——轴对称
探索等腰三角形的轴对称性;
理解并掌握等腰三角形的性质和判定方法;
01
02
学习目标
能用尺规作图:已知底边及底边上的高作等腰三角形.
03
复习旧知
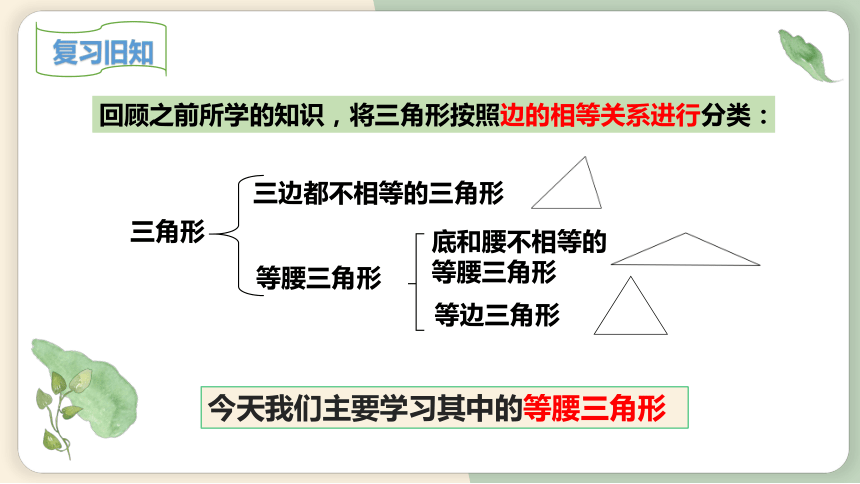
回顾之前所学的知识,将三角形按照边的相等关系进行分类:
三角形
三边都不相等的三角形
等腰三角形
底和腰不相等的等腰三角形
等边三角形
今天我们主要学习其中的等腰三角形
引入新知
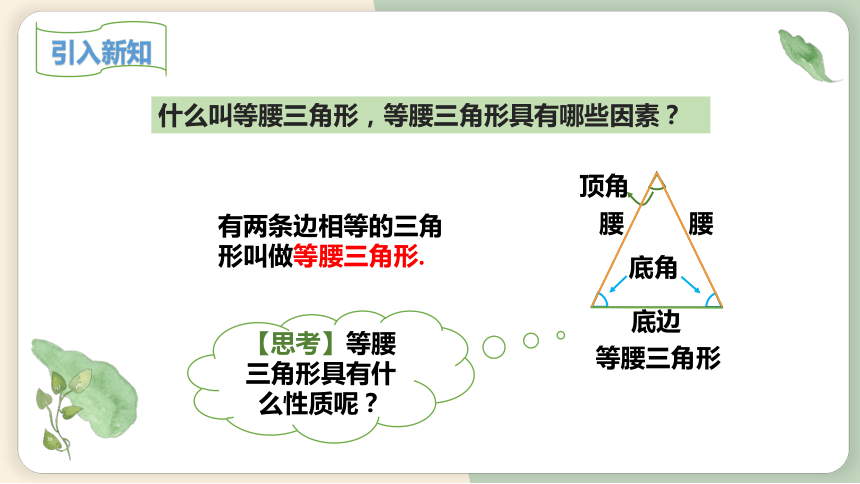
等腰三角形
腰
腰
底边
底角
顶角
什么叫等腰三角形,等腰三角形具有哪些因素?
有两条边相等的三角形叫做等腰三角形.
【思考】等腰三角形具有什么性质呢?
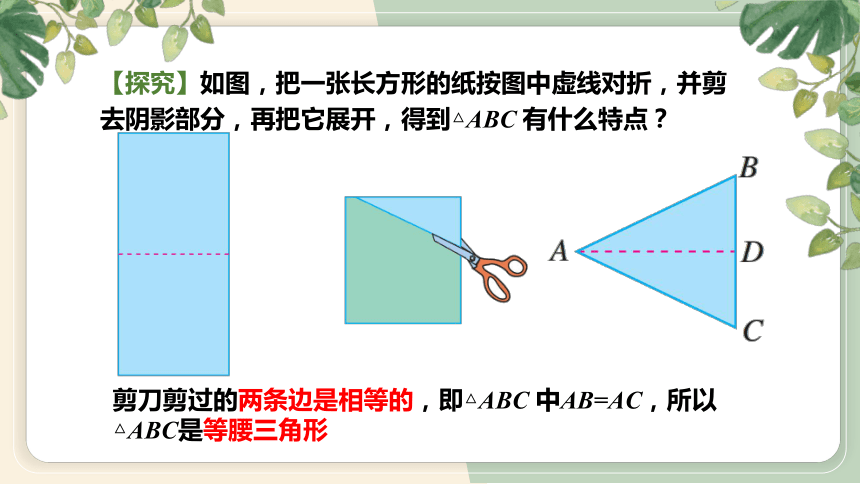
【探究】如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到△ABC 有什么特点?
剪刀剪过的两条边是相等的,即△ABC 中AB=AC,所以△ABC是等腰三角形
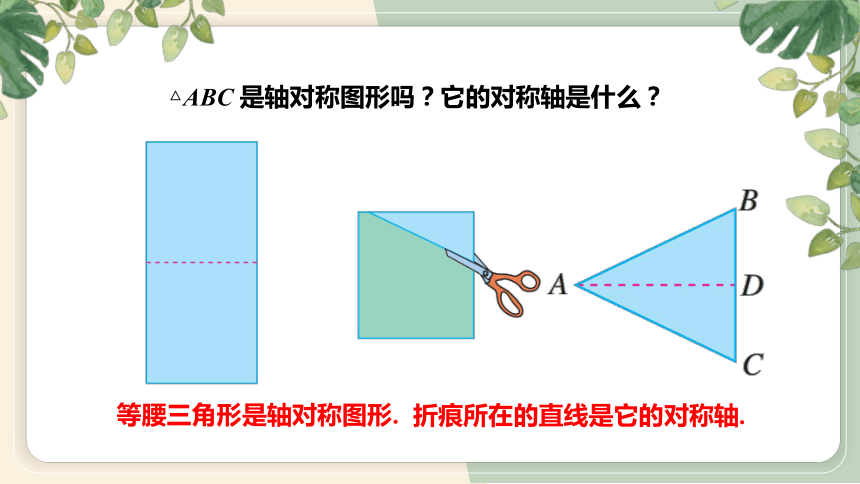
△ABC 是轴对称图形吗?它的对称轴是什么?
折痕所在的直线是它的对称轴.
等腰三角形是轴对称图形.
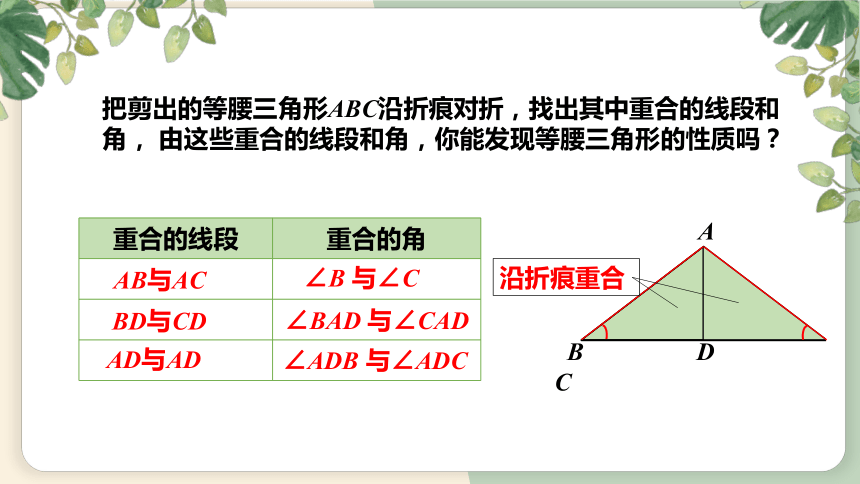
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角, 由这些重合的线段和角,你能发现等腰三角形的性质吗?
重合的线段 重合的角
AB与AC
BD与CD
AD与AD
∠B 与∠C
∠BAD 与∠CAD
∠ADB 与∠ADC
A
B D C
沿折痕重合
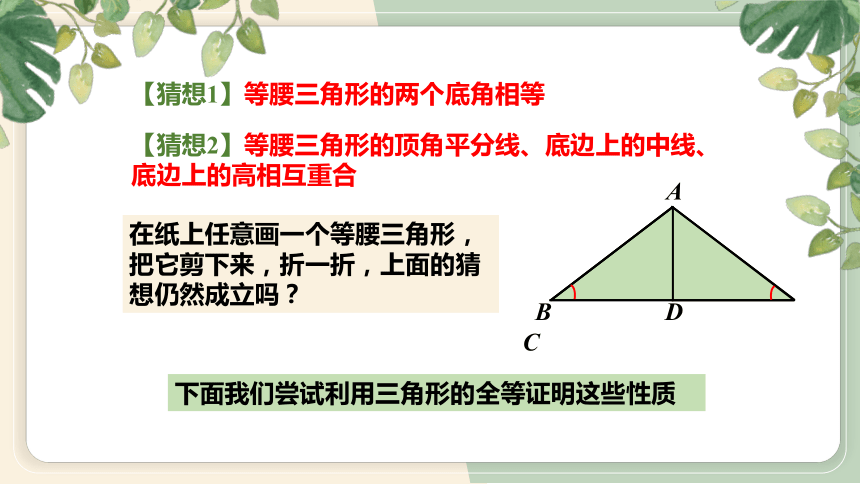
【猜想1】等腰三角形的两个底角相等
A
B D C
【猜想2】等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
在纸上任意画一个等腰三角形,把它剪下来,折一折,上面的猜想仍然成立吗?
下面我们尝试利用三角形的全等证明这些性质
A
B
C
D
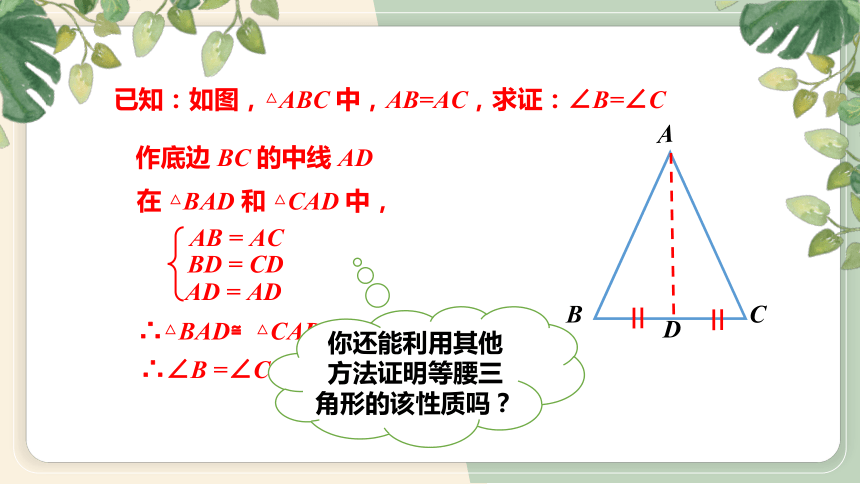
已知:如图,△ABC 中,AB=AC,求证:∠B=∠C
作底边 BC 的中线 AD
AB = AC
BD = CD
AD = AD
∴△BAD≌△CAD (SSS).
∴∠B =∠C .
在 △BAD 和 △CAD 中,
你还能利用其他方法证明等腰三角形的该性质吗?
A
B
C
D
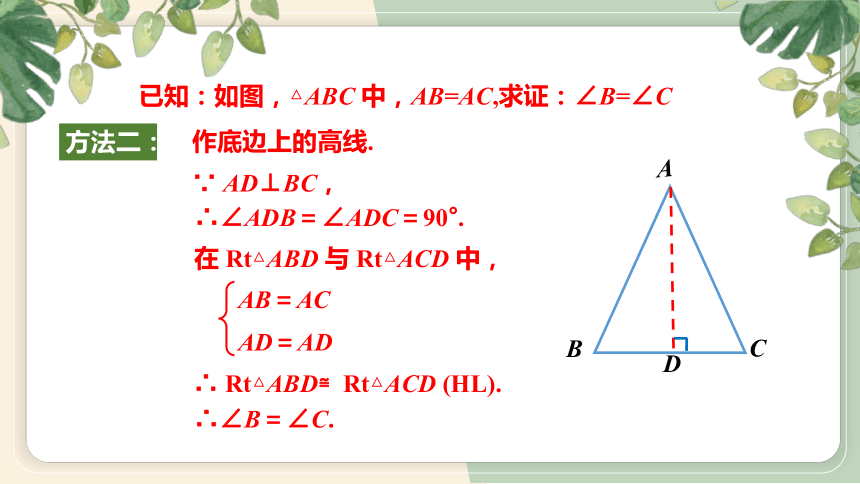
已知:如图,△ABC 中,AB=AC,求证:∠B=∠C
作底边上的高线.
方法二:
在 Rt△ABD 与 Rt△ACD 中,
AB=AC
AD=AD
∵ AD⊥BC,
∴∠B=∠C.
∴ Rt△ABD≌Rt△ACD (HL).
∴∠ADB=∠ADC=90°.
A
B
C
D
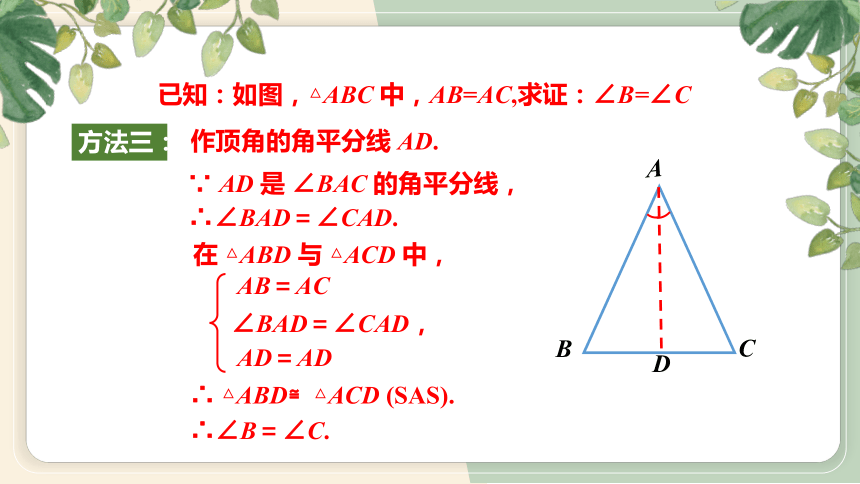
已知:如图,△ABC 中,AB=AC,求证:∠B=∠C
在 △ABD 与 △ACD 中,
AB=AC
∠BAD=∠CAD,
AD=AD
∵ AD 是 ∠BAC 的角平分线,
作顶角的角平分线 AD.
∴∠B=∠C.
∴ △ABD≌△ACD (SAS).
∴∠BAD=∠CAD.
方法三:
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
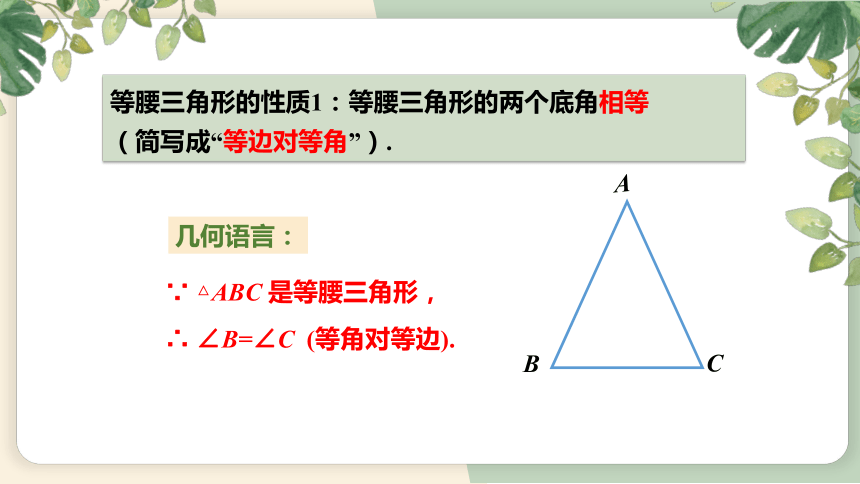
等腰三角形的性质1:等腰三角形的两个底角相等
(简写成“等边对等角”).
几何语言:
∵ △ABC 是等腰三角形,
∴ ∠B=∠C (等角对等边).
A
B
C
在上述不同方法的证明过程中,由三角形顶角作的底边上的中线、高线、顶角角平分线有什么特点?
A
B
C
D
A
B
C
D
A
B
C
D
完全重合
尝试证明猜想二,等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
已知:如图,在△ABC 中,AB = AC,BD = DC,求证 AD⊥BC,DA 平分∠BAC.
证明:∵AB = AC,BD = DC,
∴∠ADB =∠ADC =90°即AD⊥BC.
∵∠ADB +∠ADC = 180°,
∴ ∠BAD =∠CAD,∠ADB=∠ADC.
∴△BAD≌△CAD (SSS).
∴在△ABD 和△ADC 中,
AB=AC ,
AD=AD ,
BD = DC .
∴底边 BC 的中线也是∠A 的平分线和底边上的高.
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称“三线合一”)
【注意】腰上的高和中线与底角的平分线不具有这一性质
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
几何语言:
(1)∵△ABC是等腰三角形,BD = CD (已知)
∴______________,________ (等腰三角形的“三线合一”)
(2)∵△ABC是等腰三角形,∠BAD=∠CAD (已知)
∴_________,AD⊥BC,_________________________
(3)∵△ABC 是等腰三角形,AD⊥BC
∴BD = CD,______________(等腰三角形的“三线合一”)
∠BAD =∠CAD
AD⊥BC
BD = CD
(等腰三角形的“三线合一”)
∠BAD =∠CAD
例题练习
A
B
C
D
如图,在△ABC 中,AB = AC,点 D 在 AC 上,且 BD = BC = AD,求 △ABC 各角的度数.
解:∵ AB = AC,BD = BC = AD,
∴∠A = 36°,∠ABC =∠C = 72°.
解得 x = 36°.
于是在△ABC 中,有∠A +∠ABC +∠C = x + 2x + 2x = 180°,
设∠A = x,则∠BDC = ∠A+ ∠ABD = 2x,
从而∠ABC = ∠C = ∠BDC =2x,
∴∠ABC =∠C =∠BDC,∠A =∠ABD.(等边对等角)
【探究】如果一个三角形有两条边相等,那么它们所对的角相等.反之,如果一个三角形有两个角相等,那么它们所对的边有什么关系呢?
相等?
已知:如图,在△ABC 中,∠B =∠C.求证:AB = AC.
分析:
构造两个全等三角形
证明边相等
作∠BAC 的
角平分线
作BC边上的高
添加“BC边上的中线 ”
这条辅助线可以吗?
SSA(╳)
AAS(√)
AAS(√)
在△ABD和△ACD中,
∠1=∠2,
∴ △ABD≌△ACD(AAS).
∠B=∠C,
AD=AD,
∴AB=AC.
证明:过点A作AD平分∠BAC交BC于点D.
∴∠1=∠2,
方法一
D
1
2
在△ABE和△ACE中 ,
∴∠AEB=∠AEC = 90°,
证明:过点A作AE⊥BC交BC于点E.
∠AEB=∠AEC,
∠B=∠C,
AE=AE,
∴ △ABE≌△ACE(AAS).
∴AB=AC.
方法二
E
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
等腰三角形的判定:如果有一个三角形的两个角相等,那么这两个角所对的边也相等. (简写成“等角对等边”)
几何语言:
∵ 在△ABC 中,∠B =∠C,
∴AB=AC. (等角对等边)
即△ABC为等腰三角形.
例题练习
A
B
C
E
(
(
1
2
D
求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:如图,∠CAE 是△ABC 的外角,∠1 =∠2,AD∥BC.
求证:AB = AC.
分析:
证明 AB = AC
先证明 ∠B = ∠C
利用∠1 =∠2,AD∥BC
例题练习
已知:如图,∠CAE 是△ABC 的外角,∠1 =∠2,AD∥BC.
求证:AB = AC.
∴ AB = AC(__________).
∴∠1 =∠B (_______________________),
∠2 =∠C (_______________________).
证明:∵ AD∥BC,
两直线平行,同位角相等
两直线平行,内错角相等
等角对等边
∴∠B =∠C,
又∵∠1 =∠2,
A
B
C
E
(
(
1
2
D
例题练习
已知等腰三角形底边长为 a,底边上的高的长为 h,求作这个等腰三角形.
(4) 连接 AC,BC,则△ABC 即为所求.
(3) 在 MN 上取一点 C,使 DC = h;
(2) 作线段 AB 的垂直平分线 MN,
交 AB 于点 D;
作法:
(1) 作线段 AB = a;
D
A
等腰三角形的性质1:等腰三角形的两个底角等.(简写成“等边对等角”).
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称 “三线合一”)
等腰三角形的判定:如果有一个三角形的两个角相等,那么这两个角所对的边也相等. (简写成“等角对等边”)
等腰三角形
小结
谢谢观看
13.3.1等腰三角形
第十三章——轴对称
探索等腰三角形的轴对称性;
理解并掌握等腰三角形的性质和判定方法;
01
02
学习目标
能用尺规作图:已知底边及底边上的高作等腰三角形.
03
复习旧知
回顾之前所学的知识,将三角形按照边的相等关系进行分类:
三角形
三边都不相等的三角形
等腰三角形
底和腰不相等的等腰三角形
等边三角形
今天我们主要学习其中的等腰三角形
引入新知
等腰三角形
腰
腰
底边
底角
顶角
什么叫等腰三角形,等腰三角形具有哪些因素?
有两条边相等的三角形叫做等腰三角形.
【思考】等腰三角形具有什么性质呢?
【探究】如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到△ABC 有什么特点?
剪刀剪过的两条边是相等的,即△ABC 中AB=AC,所以△ABC是等腰三角形
△ABC 是轴对称图形吗?它的对称轴是什么?
折痕所在的直线是它的对称轴.
等腰三角形是轴对称图形.
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角, 由这些重合的线段和角,你能发现等腰三角形的性质吗?
重合的线段 重合的角
AB与AC
BD与CD
AD与AD
∠B 与∠C
∠BAD 与∠CAD
∠ADB 与∠ADC
A
B D C
沿折痕重合
【猜想1】等腰三角形的两个底角相等
A
B D C
【猜想2】等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
在纸上任意画一个等腰三角形,把它剪下来,折一折,上面的猜想仍然成立吗?
下面我们尝试利用三角形的全等证明这些性质
A
B
C
D
已知:如图,△ABC 中,AB=AC,求证:∠B=∠C
作底边 BC 的中线 AD
AB = AC
BD = CD
AD = AD
∴△BAD≌△CAD (SSS).
∴∠B =∠C .
在 △BAD 和 △CAD 中,
你还能利用其他方法证明等腰三角形的该性质吗?
A
B
C
D
已知:如图,△ABC 中,AB=AC,求证:∠B=∠C
作底边上的高线.
方法二:
在 Rt△ABD 与 Rt△ACD 中,
AB=AC
AD=AD
∵ AD⊥BC,
∴∠B=∠C.
∴ Rt△ABD≌Rt△ACD (HL).
∴∠ADB=∠ADC=90°.
A
B
C
D
已知:如图,△ABC 中,AB=AC,求证:∠B=∠C
在 △ABD 与 △ACD 中,
AB=AC
∠BAD=∠CAD,
AD=AD
∵ AD 是 ∠BAC 的角平分线,
作顶角的角平分线 AD.
∴∠B=∠C.
∴ △ABD≌△ACD (SAS).
∴∠BAD=∠CAD.
方法三:
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
等腰三角形的性质1:等腰三角形的两个底角相等
(简写成“等边对等角”).
几何语言:
∵ △ABC 是等腰三角形,
∴ ∠B=∠C (等角对等边).
A
B
C
在上述不同方法的证明过程中,由三角形顶角作的底边上的中线、高线、顶角角平分线有什么特点?
A
B
C
D
A
B
C
D
A
B
C
D
完全重合
尝试证明猜想二,等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
已知:如图,在△ABC 中,AB = AC,BD = DC,求证 AD⊥BC,DA 平分∠BAC.
证明:∵AB = AC,BD = DC,
∴∠ADB =∠ADC =90°即AD⊥BC.
∵∠ADB +∠ADC = 180°,
∴ ∠BAD =∠CAD,∠ADB=∠ADC.
∴△BAD≌△CAD (SSS).
∴在△ABD 和△ADC 中,
AB=AC ,
AD=AD ,
BD = DC .
∴底边 BC 的中线也是∠A 的平分线和底边上的高.
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称“三线合一”)
【注意】腰上的高和中线与底角的平分线不具有这一性质
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
几何语言:
(1)∵△ABC是等腰三角形,BD = CD (已知)
∴______________,________ (等腰三角形的“三线合一”)
(2)∵△ABC是等腰三角形,∠BAD=∠CAD (已知)
∴_________,AD⊥BC,_________________________
(3)∵△ABC 是等腰三角形,AD⊥BC
∴BD = CD,______________(等腰三角形的“三线合一”)
∠BAD =∠CAD
AD⊥BC
BD = CD
(等腰三角形的“三线合一”)
∠BAD =∠CAD
例题练习
A
B
C
D
如图,在△ABC 中,AB = AC,点 D 在 AC 上,且 BD = BC = AD,求 △ABC 各角的度数.
解:∵ AB = AC,BD = BC = AD,
∴∠A = 36°,∠ABC =∠C = 72°.
解得 x = 36°.
于是在△ABC 中,有∠A +∠ABC +∠C = x + 2x + 2x = 180°,
设∠A = x,则∠BDC = ∠A+ ∠ABD = 2x,
从而∠ABC = ∠C = ∠BDC =2x,
∴∠ABC =∠C =∠BDC,∠A =∠ABD.(等边对等角)
【探究】如果一个三角形有两条边相等,那么它们所对的角相等.反之,如果一个三角形有两个角相等,那么它们所对的边有什么关系呢?
相等?
已知:如图,在△ABC 中,∠B =∠C.求证:AB = AC.
分析:
构造两个全等三角形
证明边相等
作∠BAC 的
角平分线
作BC边上的高
添加“BC边上的中线 ”
这条辅助线可以吗?
SSA(╳)
AAS(√)
AAS(√)
在△ABD和△ACD中,
∠1=∠2,
∴ △ABD≌△ACD(AAS).
∠B=∠C,
AD=AD,
∴AB=AC.
证明:过点A作AD平分∠BAC交BC于点D.
∴∠1=∠2,
方法一
D
1
2
在△ABE和△ACE中 ,
∴∠AEB=∠AEC = 90°,
证明:过点A作AE⊥BC交BC于点E.
∠AEB=∠AEC,
∠B=∠C,
AE=AE,
∴ △ABE≌△ACE(AAS).
∴AB=AC.
方法二
E
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
等腰三角形的判定:如果有一个三角形的两个角相等,那么这两个角所对的边也相等. (简写成“等角对等边”)
几何语言:
∵ 在△ABC 中,∠B =∠C,
∴AB=AC. (等角对等边)
即△ABC为等腰三角形.
例题练习
A
B
C
E
(
(
1
2
D
求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:如图,∠CAE 是△ABC 的外角,∠1 =∠2,AD∥BC.
求证:AB = AC.
分析:
证明 AB = AC
先证明 ∠B = ∠C
利用∠1 =∠2,AD∥BC
例题练习
已知:如图,∠CAE 是△ABC 的外角,∠1 =∠2,AD∥BC.
求证:AB = AC.
∴ AB = AC(__________).
∴∠1 =∠B (_______________________),
∠2 =∠C (_______________________).
证明:∵ AD∥BC,
两直线平行,同位角相等
两直线平行,内错角相等
等角对等边
∴∠B =∠C,
又∵∠1 =∠2,
A
B
C
E
(
(
1
2
D
例题练习
已知等腰三角形底边长为 a,底边上的高的长为 h,求作这个等腰三角形.
(4) 连接 AC,BC,则△ABC 即为所求.
(3) 在 MN 上取一点 C,使 DC = h;
(2) 作线段 AB 的垂直平分线 MN,
交 AB 于点 D;
作法:
(1) 作线段 AB = a;
D
A
等腰三角形的性质1:等腰三角形的两个底角等.(简写成“等边对等角”).
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称 “三线合一”)
等腰三角形的判定:如果有一个三角形的两个角相等,那么这两个角所对的边也相等. (简写成“等角对等边”)
等腰三角形
小结
谢谢观看
