13.1.1轴对称 课件(共33张PPT) 初中数学人教版八年级上册
文档属性
| 名称 | 13.1.1轴对称 课件(共33张PPT) 初中数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 30.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 00:00:00 | ||
图片预览










文档简介
(共33张PPT)
13.1.1轴对称
第十三章——轴对称
COTENTS
掌握轴对称图形与两个图形关于某直线对称的区别和联系;
理解轴对称图形、两个图形关于某直线对称的概念;
01
02
学习目标
应用轴对称的性质解决简单的问题
03
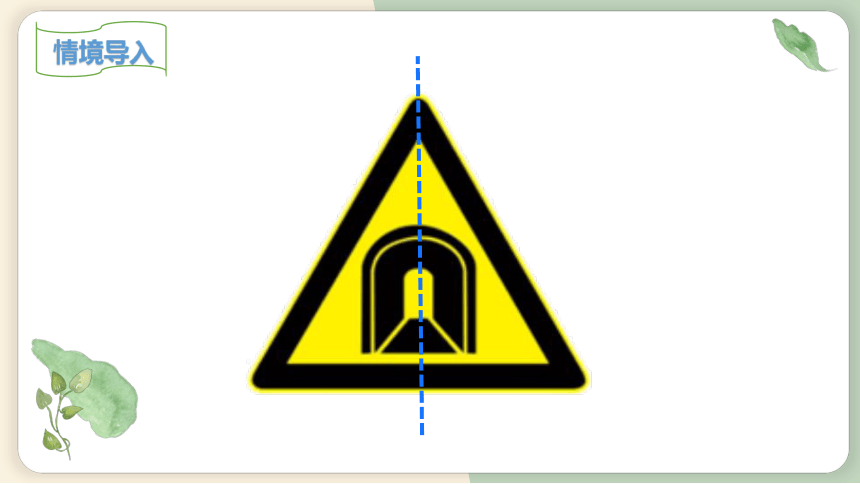
情境导入
观察下列图片,你能发现他们有什么共同的特征?
情境导入
情境导入
情境导入
情境导入
情境导入
情境导入
探究新知
如图,把一张纸对折,剪出一个图案(折痕处不要完全剪断),再打开这张对折的纸,就得到了美丽的窗花.观察得到的窗花,你能发现它们有什么共同的特点吗?
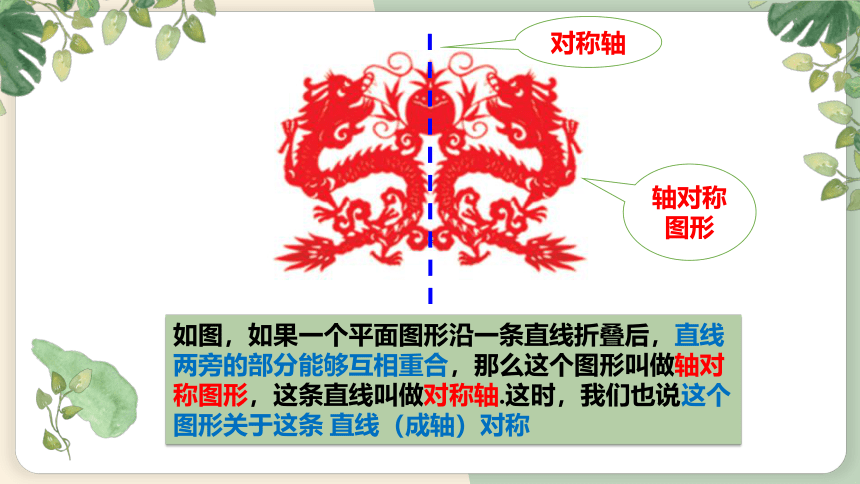
如图,如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.这时,我们也说这个图形关于这条 直线(成轴)对称
轴对称图形
对称轴
下面这些图形是轴对称图形吗?如果是,有几条对称轴?
【总结】
2.对称轴通常画成虚线,是直线,不能画成线段.
1.有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条.
剪刀
【探究】观察下面每对图形,你发现它们有什么共同特点?
共同特征:每一对图形沿着虚线折叠,左边的图形都能与右边的图形重合.
B
A
C
像这样,把一个图形沿着一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线就是对称轴.折叠后重合的点是对应点,叫做对称点.
B
A′
A
C
B′
C′
l
点 A' 是点 A 的对称点;
点 B' 是点 B 的对称点;
点 C' 是点 C 的对称点.
对称轴
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
通过学习,你能发现轴对称图形和两个图形成轴对称有什么区别与联系吗?
轴对称图形 两个图形成轴对称
图形
区别
联系 一个图形具有的特殊形状
两个全等图形的对称关系
1.都能沿着某条直线折叠后重合;都有对称轴
2.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条轴对称;如果把两个成轴对称的图形看成一个整体,那么这个图形就是轴对称图形
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【思考】如图,△ABC 和△A′B′C′关于直线MN 对称,点A′,B′,C′分别是点A,B,C 的对称点,则图中线段AA′,BB′,CC′与直线MN 有什么关系?
A
B
C
N
M
C′
A′
P
B'
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
如图所示: 点 A 与点 A′ 是对称点,设 AA′ 交对称轴MN 于点 P,将△ABC 或 △A′B′C′ 沿 MN 折叠后,点A与点 A′ 重合.
A
B
C
N
M
C′
P1
P2
A′
P
B'
AP=PA′
BP1=P1B′
CP2=P2C′
AA′⊥MN
BB′⊥MN
CC′⊥MN
对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【总结】经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.也把这条直线叫做中垂线.
符号语言:
若MN⊥AA′,垂足为P,
且 AP=A′P,则称直线MN是线段AA ′的垂直平分线.
A
B
C
N
M
C′
A′
P
B'
类似地,轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
如图,直线 l 垂直线段AA′、BB′,
直线 l 平分线段 AA′、BB′,
l
【总结】
1.图形轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线
2.轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
B
D
C
A
D
3
轴对称图形
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
小结
两个图形成轴对称
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线
轴对称
谢谢观看
13.1.1轴对称
第十三章——轴对称
COTENTS
掌握轴对称图形与两个图形关于某直线对称的区别和联系;
理解轴对称图形、两个图形关于某直线对称的概念;
01
02
学习目标
应用轴对称的性质解决简单的问题
03
情境导入
观察下列图片,你能发现他们有什么共同的特征?
情境导入
情境导入
情境导入
情境导入
情境导入
情境导入
探究新知
如图,把一张纸对折,剪出一个图案(折痕处不要完全剪断),再打开这张对折的纸,就得到了美丽的窗花.观察得到的窗花,你能发现它们有什么共同的特点吗?
如图,如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.这时,我们也说这个图形关于这条 直线(成轴)对称
轴对称图形
对称轴
下面这些图形是轴对称图形吗?如果是,有几条对称轴?
【总结】
2.对称轴通常画成虚线,是直线,不能画成线段.
1.有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条.
剪刀
【探究】观察下面每对图形,你发现它们有什么共同特点?
共同特征:每一对图形沿着虚线折叠,左边的图形都能与右边的图形重合.
B
A
C
像这样,把一个图形沿着一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线就是对称轴.折叠后重合的点是对应点,叫做对称点.
B
A′
A
C
B′
C′
l
点 A' 是点 A 的对称点;
点 B' 是点 B 的对称点;
点 C' 是点 C 的对称点.
对称轴
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
通过学习,你能发现轴对称图形和两个图形成轴对称有什么区别与联系吗?
轴对称图形 两个图形成轴对称
图形
区别
联系 一个图形具有的特殊形状
两个全等图形的对称关系
1.都能沿着某条直线折叠后重合;都有对称轴
2.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条轴对称;如果把两个成轴对称的图形看成一个整体,那么这个图形就是轴对称图形
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【思考】如图,△ABC 和△A′B′C′关于直线MN 对称,点A′,B′,C′分别是点A,B,C 的对称点,则图中线段AA′,BB′,CC′与直线MN 有什么关系?
A
B
C
N
M
C′
A′
P
B'
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
如图所示: 点 A 与点 A′ 是对称点,设 AA′ 交对称轴MN 于点 P,将△ABC 或 △A′B′C′ 沿 MN 折叠后,点A与点 A′ 重合.
A
B
C
N
M
C′
P1
P2
A′
P
B'
AP=PA′
BP1=P1B′
CP2=P2C′
AA′⊥MN
BB′⊥MN
CC′⊥MN
对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.
由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
【总结】经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.也把这条直线叫做中垂线.
符号语言:
若MN⊥AA′,垂足为P,
且 AP=A′P,则称直线MN是线段AA ′的垂直平分线.
A
B
C
N
M
C′
A′
P
B'
类似地,轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
如图,直线 l 垂直线段AA′、BB′,
直线 l 平分线段 AA′、BB′,
l
【总结】
1.图形轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线
2.轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
B
D
C
A
D
3
轴对称图形
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
小结
两个图形成轴对称
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线
轴对称
谢谢观看
