14.2.2完全平方公式 课件(共31张PPT) 初中数学人教版八年级上册
文档属性
| 名称 | 14.2.2完全平方公式 课件(共31张PPT) 初中数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 16.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
14.2.2完全平方公式
第十四章——整式的乘法与因式分解
理解完全平方公式,能运用完全平方公式进行计算.
经历完全平方公式的探索及推导过程,掌握完全平方公式的结构特征;
01
02
学习目标
知识回顾
(a+b) (a-b) = a2-b2.
两个数的和
两个数的差
平方差
两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式:
引入新知
【探究1】计算下列多项式的积,你能发现什么规律?
(p+1)2 = = = ;
(m+2)2 = = = .
p2+2p+1
m2+4m+4
(p+1)(p+1)
(m+2)(m+2)
多项式乘多项式
两个数的和的平方
p2 + p + p + 12
m2 +2m+2m+22
【探究1】计算下列多项式的积,你能发现什么规律?
(p+1)2 = = = ;
(m+2)2 = = = .
p2+2p+1
m2+4m+4
(p+1)(p+1)
(m+2)(m+2)
p2 + 1p +1p + 12
m2 +2m+2m+22
【发现】两个数的和的平方,等于这两个数的平方和,加上这两个数的积的2倍.
探究新知
验证:
对于任意数字,探究上述发现是否仍成立?
(a+b)2 = (a+b)(a+b)
= a2+2ab+b2.
= a2 + ab + ab + b2
两个数的和的平方
两个数的平方和,加上这两个数的积的2倍
多项式乘法法则
合并同类项
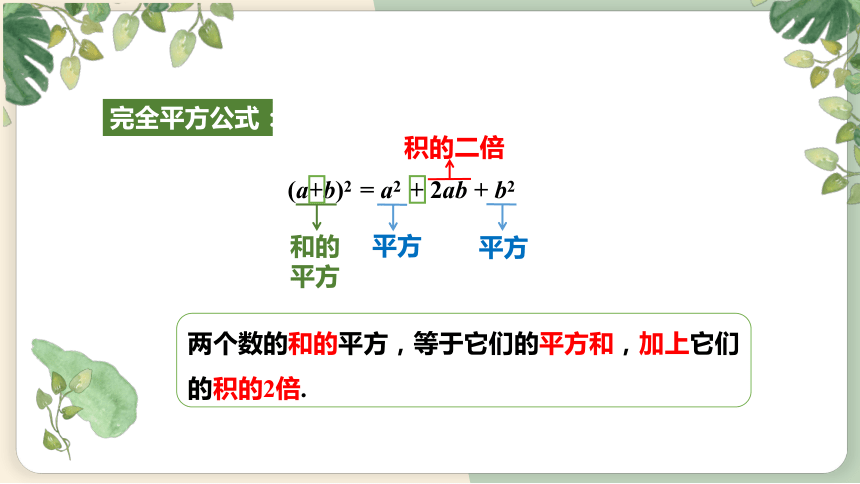
两个数的和的平方,等于它们的平方和,加上它们的积的2倍.
完全平方公式:
(a+b)2 = a2 + 2ab + b2
和的平方
平方
积的二倍
平方
【探究2】结合探究1 计算下列多项式的积,你能发现什么规律?
( p 1 )2 = = = ;
( m 2 )2 = = = .
p2 2p+1
m2 4m+4
(p 1)(p 1)
(m 2)(m 2)
多项式乘多项式
两个数的差的平方
p2 p p + 12
m2 2m 2m+22
探究新知
(p 1)2 = = = ;
(m 2)2 = = = .
【发现】两个数的差的平方,等于这两个数的平方和,减去这两个数的积的2倍.
探究新知
p2 2p+1
(p 1)(p 1)
p2 p p + 12
m2 4m+4
(m 2)(m 2)
m2 2m 2m+22
【探究2】结合探究1 计算下列多项式的积,你能发现什么规律?
验证:
对于任意数字,探究上述发现是否仍成立?
两个数的差的平方
两个数的平方和,减去这两个数的积的2倍
多项式乘法法则
合并同类项
(a-b)2 = (a-b)(a-b)
= a2-2ab-b2.
= a2 - ab - ab - b2
两个数的差的平方,等于它们的平方和,减去它们的积的2倍.
完全平方公式:
(a - b)2 = a2 - 2ab + b2
差的平方
平方
积的二倍
平方
完全平方公式:
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
b
a
a
b
a2
ab
ab
b2
你能根据图1和图2中图形的面积说明完全平方公式吗
(a-b)2
a
b
b
a
ab
ab
b2
图 1
图2
b
a
a
b
a2
ab
ab
b2
图 1
如图,边长为 (a + b) 的正方形的面积是 .
(a+b)2
它的面积还可以视为两个小正方形和两个小长方形面积的和:
.
a2+ab+ab+b2 = a2+2ab+b2
【结论】 (a+b)2 = a2+2ab+b2
如图,边长为 (a b) 的正方形的面积是 .
(a b)2
它的面积还可以视为大正方形的面积减去两个小长方形面积的差:
.
a2 ab ab+b2 = a2+2ab+b2
【结论】 (a b)2 = a2 2ab+b2
(a-b)2
a
b
b
a
ab
ab
b2
图2
例题练习
运用完全平分公式计算:
(1) (4m+n)2 ;
(2) (y )2
解:(1) (4m+n)2=(4m)2+2 (4m) n+n2
= 16m2+8mn+n2;
(2) ( y )2
= y2 2 y +( )2
= y2 y + .
探究新知
思考:
(a+b)2 与 ( a b)2 相等吗?
(a b)2 与 (b a)2 相等吗?
(a b)2 与 a2 b2 相等吗?
( a b)2=[ (a+b)]2=(a+b)2
相等
相等
(a b)2 (a2 b2)=2b2 2ab
不一定相等
若2b2 2ab=0,则b2=ab.
当a=b或b=0时,两式相等.
(b a)2=[ (a b)]2=(a b)2
探究新知
回顾之前所学的去括号法则吗?试着去掉下面式子中的括号.
a+(b+c)=
a–(b+c)=
a+b+c
a–b–c
把上面两个等式的左右两边对换,等式仍成立,
即 a + b + c = a + (b + c);a – b – c = a – (b + c).
添括号法则
探究新知
将等号左右两边对换,等式仍然成立.
a+b+c=a+(b+c)
a b c=a (b+c)
符号不变
符号不变
添上“+( )”,括号里的各项都不变符号.
符号改变
符号改变
添上“ ( )”,括号里的各项都改变符号.
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
6
25
12
49
4或-4
16或-16
8
小结
完全平方公式:
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
添括号法则:
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
谢谢观看
14.2.2完全平方公式
第十四章——整式的乘法与因式分解
理解完全平方公式,能运用完全平方公式进行计算.
经历完全平方公式的探索及推导过程,掌握完全平方公式的结构特征;
01
02
学习目标
知识回顾
(a+b) (a-b) = a2-b2.
两个数的和
两个数的差
平方差
两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式:
引入新知
【探究1】计算下列多项式的积,你能发现什么规律?
(p+1)2 = = = ;
(m+2)2 = = = .
p2+2p+1
m2+4m+4
(p+1)(p+1)
(m+2)(m+2)
多项式乘多项式
两个数的和的平方
p2 + p + p + 12
m2 +2m+2m+22
【探究1】计算下列多项式的积,你能发现什么规律?
(p+1)2 = = = ;
(m+2)2 = = = .
p2+2p+1
m2+4m+4
(p+1)(p+1)
(m+2)(m+2)
p2 + 1p +1p + 12
m2 +2m+2m+22
【发现】两个数的和的平方,等于这两个数的平方和,加上这两个数的积的2倍.
探究新知
验证:
对于任意数字,探究上述发现是否仍成立?
(a+b)2 = (a+b)(a+b)
= a2+2ab+b2.
= a2 + ab + ab + b2
两个数的和的平方
两个数的平方和,加上这两个数的积的2倍
多项式乘法法则
合并同类项
两个数的和的平方,等于它们的平方和,加上它们的积的2倍.
完全平方公式:
(a+b)2 = a2 + 2ab + b2
和的平方
平方
积的二倍
平方
【探究2】结合探究1 计算下列多项式的积,你能发现什么规律?
( p 1 )2 = = = ;
( m 2 )2 = = = .
p2 2p+1
m2 4m+4
(p 1)(p 1)
(m 2)(m 2)
多项式乘多项式
两个数的差的平方
p2 p p + 12
m2 2m 2m+22
探究新知
(p 1)2 = = = ;
(m 2)2 = = = .
【发现】两个数的差的平方,等于这两个数的平方和,减去这两个数的积的2倍.
探究新知
p2 2p+1
(p 1)(p 1)
p2 p p + 12
m2 4m+4
(m 2)(m 2)
m2 2m 2m+22
【探究2】结合探究1 计算下列多项式的积,你能发现什么规律?
验证:
对于任意数字,探究上述发现是否仍成立?
两个数的差的平方
两个数的平方和,减去这两个数的积的2倍
多项式乘法法则
合并同类项
(a-b)2 = (a-b)(a-b)
= a2-2ab-b2.
= a2 - ab - ab - b2
两个数的差的平方,等于它们的平方和,减去它们的积的2倍.
完全平方公式:
(a - b)2 = a2 - 2ab + b2
差的平方
平方
积的二倍
平方
完全平方公式:
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
b
a
a
b
a2
ab
ab
b2
你能根据图1和图2中图形的面积说明完全平方公式吗
(a-b)2
a
b
b
a
ab
ab
b2
图 1
图2
b
a
a
b
a2
ab
ab
b2
图 1
如图,边长为 (a + b) 的正方形的面积是 .
(a+b)2
它的面积还可以视为两个小正方形和两个小长方形面积的和:
.
a2+ab+ab+b2 = a2+2ab+b2
【结论】 (a+b)2 = a2+2ab+b2
如图,边长为 (a b) 的正方形的面积是 .
(a b)2
它的面积还可以视为大正方形的面积减去两个小长方形面积的差:
.
a2 ab ab+b2 = a2+2ab+b2
【结论】 (a b)2 = a2 2ab+b2
(a-b)2
a
b
b
a
ab
ab
b2
图2
例题练习
运用完全平分公式计算:
(1) (4m+n)2 ;
(2) (y )2
解:(1) (4m+n)2=(4m)2+2 (4m) n+n2
= 16m2+8mn+n2;
(2) ( y )2
= y2 2 y +( )2
= y2 y + .
探究新知
思考:
(a+b)2 与 ( a b)2 相等吗?
(a b)2 与 (b a)2 相等吗?
(a b)2 与 a2 b2 相等吗?
( a b)2=[ (a+b)]2=(a+b)2
相等
相等
(a b)2 (a2 b2)=2b2 2ab
不一定相等
若2b2 2ab=0,则b2=ab.
当a=b或b=0时,两式相等.
(b a)2=[ (a b)]2=(a b)2
探究新知
回顾之前所学的去括号法则吗?试着去掉下面式子中的括号.
a+(b+c)=
a–(b+c)=
a+b+c
a–b–c
把上面两个等式的左右两边对换,等式仍成立,
即 a + b + c = a + (b + c);a – b – c = a – (b + c).
添括号法则
探究新知
将等号左右两边对换,等式仍然成立.
a+b+c=a+(b+c)
a b c=a (b+c)
符号不变
符号不变
添上“+( )”,括号里的各项都不变符号.
符号改变
符号改变
添上“ ( )”,括号里的各项都改变符号.
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
6
25
12
49
4或-4
16或-16
8
小结
完全平方公式:
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
添括号法则:
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
谢谢观看
