人教版(2024)八年级上册12.2 三角形全等的判定 同步练习(无答案)
文档属性
| 名称 | 人教版(2024)八年级上册12.2 三角形全等的判定 同步练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 271.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-12 08:46:24 | ||
图片预览

文档简介
12.2 三角形全等的判定 同步练习
一、选择题
如图,已知 ,则不一定能使 的条件是
A. B.
C. D.
如图,点 , 在 上,,,要使 ,还需要添加的一个条件是
A. B. C. D.
对于 与 ,已知 ,,则下列条件① ;② ;③ ;④ 中能判定它们全等的有
A.①② B.①③ C.②③ D.③④
下列四个条件中,能证明两个直角三角形全等的是
A.两个锐角相等 B.一条直角边相等
C.两条直角边对应相等 D.斜边对应相等
如图,小明不小心把一块三角形形状的玻璃打碎成了三块,他想要到玻璃店去配一块大小、形状完全一样的玻璃,你认为应该带的是
A.① B.② C.③ D.①和②
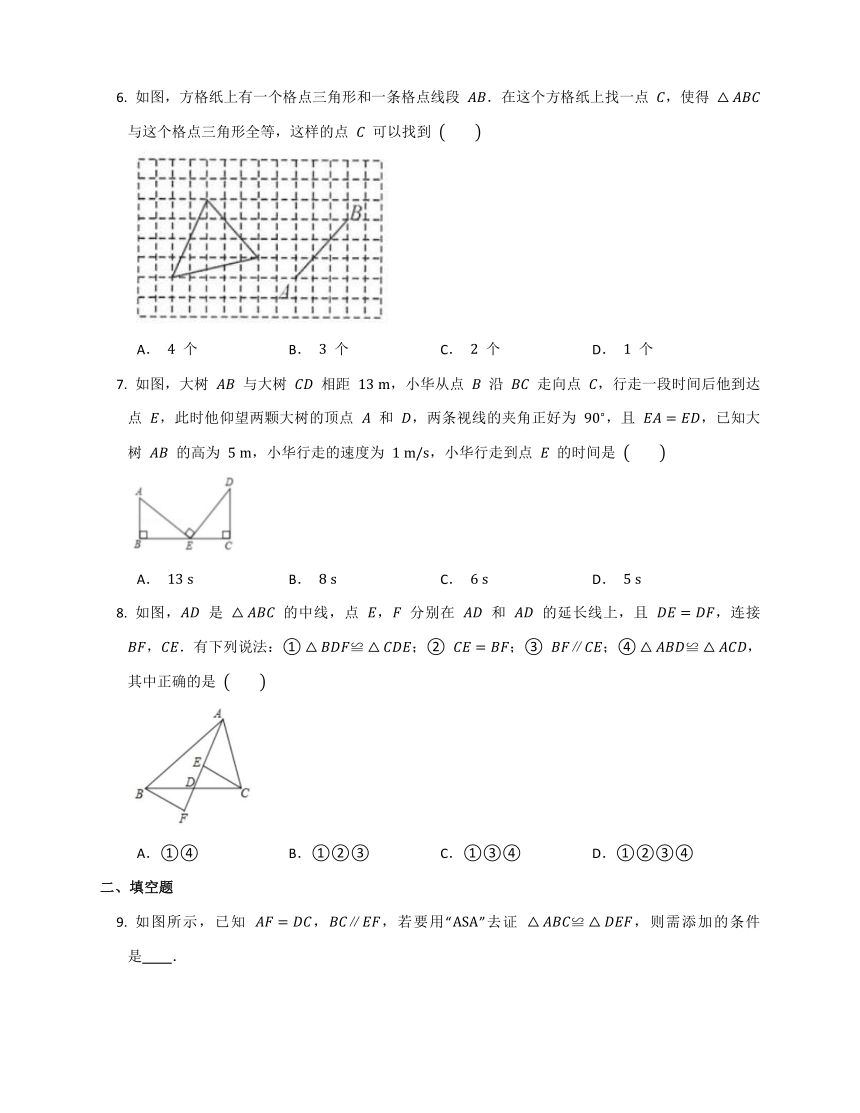
如图,方格纸上有一个格点三角形和一条格点线段 .在这个方格纸上找一点 ,使得 与这个格点三角形全等,这样的点 可以找到
A. 个 B. 个 C. 个 D. 个
如图,大树 与大树 相距 ,小华从点 沿 走向点 ,行走一段时间后他到达点 ,此时他仰望两颗大树的顶点 和 ,两条视线的夹角正好为 ,且 ,已知大树 的高为 ,小华行走的速度为 ,小华行走到点 的时间是
A. B. C. D.
如图, 是 的中线,点 , 分别在 和 的延长线上,且 ,连接 ,.有下列说法:① ;② ;③ ;④ ,其中正确的是
A.①④ B.①②③ C.①③④ D.①②③④
二、填空题
如图所示,已知 ,,若要用“”去证 ,则需添加的条件是 .
如图,把 的中线 延长到点 ,使 ,连接 ,若 且 的周长比 的周长大 ,则 .
如图, 点为 的边 中点,,过 点作直线交 与 点,交 于 点,若 ,,则 .
如图,已知 ,, 与 相交于点 ,如果 经过点 ,点 , 分别在 , 上,那么图中的全等三角形共有 对.
已知:在 与 中,,,,,且 ,则这两个三角形 (选填“全等”或“不全等”).
如图,点 和动点 在直线 上,点 关于点 的对称点为点 ,以 为边作 ,使 ,.直线 上有一点 在点 右侧,,过点 作射线 ,点 为射线 上的一个动点,连接 .当 与 全等时, 的长度为 .
三、解答题(共6题)
如图,已知 ,,.
(1) 全等吗?为什么?
(2) 连接 ,,那么 , 相等吗?为什么?
如图,已知 ,,.
(1) 与 全等吗?为什么?
(2) 如果 , 相交于点 ,连接 ,你还能找出哪几对全等三角形?并直接写出所用的判定方法.
如图,在 中,已知 ,垂足是点 ,,.试说明 的理由.
如图,,,点 在 上,且 .求证:.
如图,在 中, 是边 上的点,,,垂足分别为 ,,且 ,.求证:.
如图,已知 ,,, 分别是 , 的中点,说明 的理由.
一、选择题
如图,已知 ,则不一定能使 的条件是
A. B.
C. D.
如图,点 , 在 上,,,要使 ,还需要添加的一个条件是
A. B. C. D.
对于 与 ,已知 ,,则下列条件① ;② ;③ ;④ 中能判定它们全等的有
A.①② B.①③ C.②③ D.③④
下列四个条件中,能证明两个直角三角形全等的是
A.两个锐角相等 B.一条直角边相等
C.两条直角边对应相等 D.斜边对应相等
如图,小明不小心把一块三角形形状的玻璃打碎成了三块,他想要到玻璃店去配一块大小、形状完全一样的玻璃,你认为应该带的是
A.① B.② C.③ D.①和②
如图,方格纸上有一个格点三角形和一条格点线段 .在这个方格纸上找一点 ,使得 与这个格点三角形全等,这样的点 可以找到
A. 个 B. 个 C. 个 D. 个
如图,大树 与大树 相距 ,小华从点 沿 走向点 ,行走一段时间后他到达点 ,此时他仰望两颗大树的顶点 和 ,两条视线的夹角正好为 ,且 ,已知大树 的高为 ,小华行走的速度为 ,小华行走到点 的时间是
A. B. C. D.
如图, 是 的中线,点 , 分别在 和 的延长线上,且 ,连接 ,.有下列说法:① ;② ;③ ;④ ,其中正确的是
A.①④ B.①②③ C.①③④ D.①②③④
二、填空题
如图所示,已知 ,,若要用“”去证 ,则需添加的条件是 .
如图,把 的中线 延长到点 ,使 ,连接 ,若 且 的周长比 的周长大 ,则 .
如图, 点为 的边 中点,,过 点作直线交 与 点,交 于 点,若 ,,则 .
如图,已知 ,, 与 相交于点 ,如果 经过点 ,点 , 分别在 , 上,那么图中的全等三角形共有 对.
已知:在 与 中,,,,,且 ,则这两个三角形 (选填“全等”或“不全等”).
如图,点 和动点 在直线 上,点 关于点 的对称点为点 ,以 为边作 ,使 ,.直线 上有一点 在点 右侧,,过点 作射线 ,点 为射线 上的一个动点,连接 .当 与 全等时, 的长度为 .
三、解答题(共6题)
如图,已知 ,,.
(1) 全等吗?为什么?
(2) 连接 ,,那么 , 相等吗?为什么?
如图,已知 ,,.
(1) 与 全等吗?为什么?
(2) 如果 , 相交于点 ,连接 ,你还能找出哪几对全等三角形?并直接写出所用的判定方法.
如图,在 中,已知 ,垂足是点 ,,.试说明 的理由.
如图,,,点 在 上,且 .求证:.
如图,在 中, 是边 上的点,,,垂足分别为 ,,且 ,.求证:.
如图,已知 ,,, 分别是 , 的中点,说明 的理由.
