2024年山西省长治市中考数学模拟预测试题(含答案)
文档属性
| 名称 | 2024年山西省长治市中考数学模拟预测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 832.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 22:27:18 | ||
图片预览




文档简介
姓名__________ 准考证号__________
2024年山西省初中学业水平测试信息卷
数 学
注意事项:
1.本试卷分第Ⅰ卷和第Ⅱ卷两部分.本试卷共8页,满分120分,考试时间120分钟.
2.答卷前,考生务必将自已的姓名、准考证号填写在本试卷相应的位置.
3.答案全部在答题卡上完成,答在本试卷上无效.
4.考试结束后,将本试卷与答题卡一并交回.
第Ⅰ卷 选择题(共30分)
一、选择题(本大题共10小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑.)
1.在2024年,科技发展迅速,人工智能和大数据在各个领域都得到了广泛的应用,同时2024年人们的环境保护意识也得到了提高,可再生能源的使用更加广泛.的相反数是( ).
A. B. C. D.2024
2.下列运算正确的是( ).
A. B. C. D.
3.国家电影局2月18日发布数据,我国2024年春节档电影票房达80.16亿元,创造了新的春节档票房纪录,观影人次为1.63亿.将数据80.16亿用科学记数法表示为( ).
A. B. C. D.
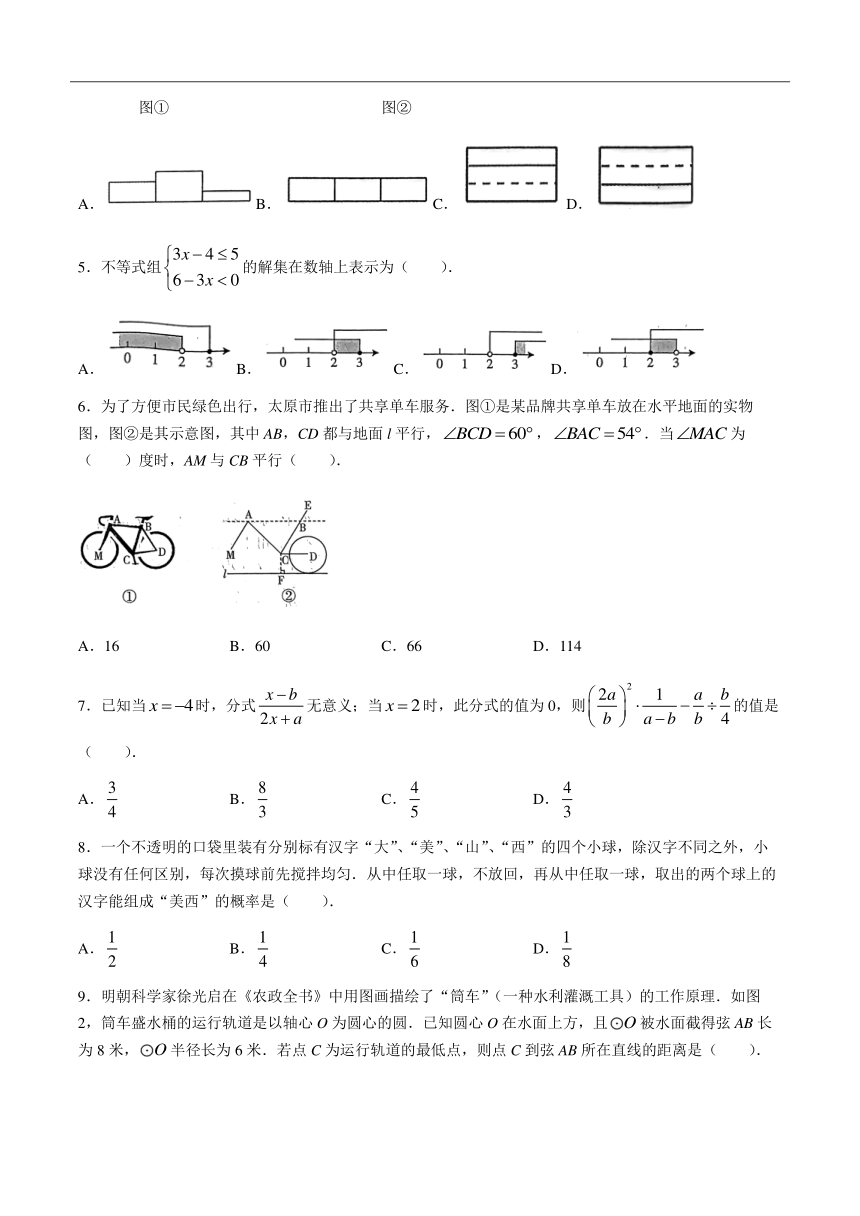
4.中国代表团在杭州亚运会共收获201金、111银、71铜,总计383枚奖牌,创历史纪录.图①是2023年10月2日乒乓球男单颁奖现场.图②是领奖台的示意图,则此领奖台的主视图是( ).
图① 图②
A.B.C.D.
5.不等式组的解集在数轴上表示为( ).
A.B.C.D.
6.为了方便市民绿色出行,太原市推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,,.当为( )度时,AM与CB平行( ).
A.16 B.60 C.66 D.114
7.已知当时,分式无意义;当时,此分式的值为0,则的值是( ).
A. B. C. D.
8.一个不透明的口袋里装有分别标有汉字“大”、“美”、“山”、“西”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.从中任取一球,不放回,再从中任取一球,取出的两个球上的汉字能组成“美西”的概率是( ).
A. B. C. D.
9.明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”(一种水利灌溉工具)的工作原理.如图2,筒车盛水桶的运行轨道是以轴心O为圆心的圆.已知圆心O在水面上方,且被水面截得弦AB长为8米,半径长为6米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( ).
图1 图2
A.2米 B.4米 C.米 D.米
10.题目:“如图,已知抛物线,点是y轴上的一点,将点M向右平移5个单位长度得到点N,若线段MN与L只有一个公共点,直接写出n的取值范围.”对于其答案,甲答:,乙答:,丙答:,丁答:,则下列说法正确的是( ).
A.只有甲答的对 B.甲、乙答案合在一起才完整
C.甲、丙答案合在一起才完整 D.甲、丁答案合在一起才完整
第Ⅱ卷 非选择题(共90分)
二、填空题(本大题共5个小题,每小题3分,共15分)
11.在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式因式分解的结果是,若取,时,则各个因式的值是:,,,把这些值从小到大排列得到016128,于是就可以把“016128”作为一个六位数的密码,对于多项式,取,时,请你写出用上述方法产生的密码__________.
12.2023年11月20日,“第40届太原双塔牡丹文化节”精彩集锦登上美国纽约时代广场大屏,国色牡丹“走”向世界,锦绣太原“火”遍全球.在公园内,牡丹按正方形形状种植,在它的周围种植芍药,如图反映了牡丹的列数(n)和芍药的数量规律,那么当时,芍药的数量为__________株.
……
13.在两个不透明的袋子中分别装有一些除颜色外完全相同的球.甲袋中装有2个白球、1个黄球,乙袋中装有1个白球、2个黄球,这些球除颜色外无其他差别,在看不到球的情况下,从两个袋子中各随机摸出一个球,摸出的两个球的颜色都是白色的概率是__________.
14.如图,在一坡度的斜面上,一木箱沿斜面向上推进了10米,则木箱升高了__________米.
15.如图,在平面直角坐标系中,正方形ABCD的边长为4,,则点C的坐标为__________.
三、解答题(本大题共8个小题,共75分.解答应写出文字说明、证明过程或演算步骤.)
16.(本题共2个小题,每小题4分,共8分)
(1)计算:;
(2)解方程组:.
17.(本题8分)
如图,一次函数的图象与反比例函数的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知点A坐标为,点B的坐标为.
(1)求反比例函数的解析式和一次函数的解析式;
(2)连接OA,OB,求的面积;
(3)观察图象直接写出时,x的取值范围是__________.
18.(本题8分)
2023年10月10日,《2023年度中国精神心理健康》蓝皮书发布.中学生心理健康受到社会的广泛关注,某校开展心理健康教育专题讲座,就学生对心理健康知识的了解程度,采用随机抽样调查的方式,根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
扇形统计图 条形统计图
(1)接受问卷调查的学生共有__________人,条形统计图中m的值为__________,扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为__________;
(2)若该校共有学生800人,根据上述调查结果,可以估计出该校学生中对心理健康知识“不了解”的总人数为__________人;
(3)若某班要从对心理健康知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加心理健康知识竞赛;请用列表或画树状图的方法,求恰好抽到2名女生的概率.
19.(本题9分)阅读与思考:
【阅读材料】如图1,点A是外一点,点P是上一动点.若的半径为3,OA长度为5,则根据:,得到点P到点A的最短距离为:.
解决问题:
(1)如图2,已知正方形ABCD的边长为4,点M,N分别从点B,C同时出发,以相同的速度沿边BC,CD方向向终点C和D运动,连接AM和BN交于点P.
①证明:≌;
②求点P到点C的最短距离.
图1 图2 图3
(2)如图3,在平面直角坐标系中,等边的边OB在x轴正半轴上,点,,点D从点B出发,沿BO运动到点O,点E同时从点O以相同的速度出发,沿OA运动到点A,连接AD,BE,交点为点F,点M是y轴上一点,直接写出FM的最小值.
20.(本题9分)
“畅游山西,逛代县边靖楼”成为今年山西旅游新特色.某数学兴趣小组用无人机测量边靖楼AB的高度,测量方案如图:在坡底D处测得塔顶A的仰角为,沿坡比为的斜坡CD前行26米到达平台C处,在C处测得塔顶A的仰角为.
(1)求坡顶C到地面的距离;
(2)计算边靖楼AB的高度.
21.(本题9分)
2023年11月28日,2023龙芯产品发布暨用户大会举行.芯片目前是全球紧缺资源,某市政府通过招商引进“芯屏汽合、集终生智”等优势产业,发展新兴产业,某芯片公司引进了一条内存芯片生产线,开工第一季度生产300万个,第三季度生产432万个.试回答下列问题:
(1)已知每季度生产量的平均增长率相等,求前三季度生产量的平均增长率;
(2)经调查发现,1条生产线最大产能是600万个/季度,若每增加1条生产线,每条生产线的最大产能将减少20万个/季度,现该公司要保证每季度生产内存芯片2600万个,在增加产能同时又要节省投入成本的条件下(生产线越多,投入成本越大),应该再增加几条生产线?
22.(本题11分)综合与实践:
【问题情境】某数学兴趣小组在学完《平行四边形》之后,研究了新人教版数学教材第64页的数学活动1.其内容如下:
如果我们身旁没有量角器或三角尺,又需要作,,等大小的角,可以采用下面的方法(如图1); (1)对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平. (2)再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM.同时,得到了线段BN.
【知识运用】请根据上述过程完成下列问题:
图1 图2
(1)已知矩形纸片ABCD,,.求线段BM的长;
(2)通过观察猜测的度数是多少?并进行证明;
【综合提升】
(3)乐乐在探究活动的第(2)步基础上再次动手操作(如图2),将MN延长交BC于点G.将沿MG折叠,点B刚好落在AD边上点H处,连接GH,把纸片再次展平.请判断四边形BGHM的形状,并说明理由.
23.(本题13分)综合与探究:
如图,在平面直角坐标系中,抛物线与x轴交于点和点C,与y轴交于点,点P是抛物线上点A与点C之间的动点(不包括点A,点C).
备用图
(1)求抛物线的解析式;
(2)动点P在抛物线上,且在直线AB上方,求面积的最大值及此时点P的坐标;
(3)在(2)的条件下,将该抛物线向右平移2.5个单位,点F为点P的对应点,平移后的抛物线与y轴交于点E,Q为平移后的抛物线的对称轴上任意一点.若是以QE为腰的等腰三角形.求出所有符合条件的点Q的坐标.
2024年山西省初中学业水平测试信息卷
数学参考答案
一、(每小题3分,共30分)
1 2 3 4 5 6 7 8 9 10
D B C A B C B C C B
二、(每小题3分,共15分)
11.111213 12.80 13. 14.5 15、
三、(本大题共8个小题,共75分)
16.(1)解:原式
.(4分)
(2)解:
①×2+②,得,解得:,
把代入①,得,解得:,
所以方程组的解是.(8分)
17.解:(1)∵函数经过,∴,,
∴反比例函数的解析式是.(1分)
经过点,则,∴.
∵一次函数的图象经过点,点,
∴,解得,
∴一次函数的解析式为.(3分)
(2)一次函数,
当时,,∴,,
∴的面积.(6分)
(3)反比例函数与一次函数交于,,
∴时x的取值范围是或.(8分)
18.解:(1)∵基本了解的有40人,占50%,
∴接受问卷调查的学生共有%=80(人),
条形统计图中m的值为:,
扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为:.
故答案为:80,16,.(3分)
(2)可以估计出该校学生中对心理健康知识“不了解”的总人数为:(人).
故答案为:40.(4分)
(3)画树状图如下:
一共有12种等可能的结果,其中恰好抽到2名女生的结果有2种,
∴P(恰好抽到2名女生).(8分)
19.(1)①证明:由题可知,
∵,,∴≌(SAS).(2分)
②解:∵≌,∴,(3分)
∵,∴,
∴,
∴P点在以AB为直径的圆上.(4分)
取AB的中点O,连接OP,PC,OC,
∴,(5分)
又∵,,
∴,(6分)
∴PC的最短距离是.(7分)
(2)(9分)
提示:
20.解:(1)延长AB交PQ于点E,过点C作,垂足为点F,
则,,
设米,则米,
在中,米,
∴,∴,
解得,(负值舍去),
∴米,米,
即坡顶C到地面的距离为10米.(4分)
(2)设米,
在中,,
∴,;
在中,,,
∴,
∴,∴,解得,
∴米,
即边靖楼AB的高度为米.(9分)
21.解:(1)设前三季度生产量的平均增长率为x,
依题意得:,(2分)
解得:%,(不符合题意,舍去),
答:前三季度生产量的平均增长率为20%.(4分)
(2)设应该再增加m条生产线,
则每条生产线的最大产能为万个/季度,
依题意得:,(6分)
整理得:,
解得:,,(7分)
又∵在增加产能同时又要节省投入成本,
∴.(8分)
答:应该再增加4条生产线.(9分)
22.解:(1)∵四边形ABCD为矩形,∴,
∵,,∴.(2分)
(2)猜测:,
证明:连接AN,如图:
∵EF为折痕,∴EF垂直平分AB,∴,
∵由折叠所得,∴,
∴,则为等边三角形,
∴,∴.(7分)
(3)四边形BGHM为菱形,理由:
由题易得,BN平分,∴,
由折叠可得,∴,
又∵,∴四边形BGHM是平行四边形,
∴四边形BGHM是菱形.(11分)
23.解:(1)由抛物线经过,得:
,解得:,
∴抛物线的解析式为:.(2分)
(2)设直线AB的解析式为,
经过,得:,解得:,
∴直线AB的解析式为,
过点P作x轴的垂线交AB于点H,
设,,
则,
则面积,
即,
∴当时,面积最大值为,
此时.(7分)
(3),
则平移后的抛物线表达式为:,则点,
当时,,则点,设点,
由点Q,E,F的坐标得,
,,,
当时,则,解得:,
则点Q的坐标为:.
当时,则,解得:,
则点Q的坐标为:,
检验得点Q,点E,点F三点不共线.
综上,点Q的坐标为:或或.(13分)
2024年山西省初中学业水平测试信息卷
数 学
注意事项:
1.本试卷分第Ⅰ卷和第Ⅱ卷两部分.本试卷共8页,满分120分,考试时间120分钟.
2.答卷前,考生务必将自已的姓名、准考证号填写在本试卷相应的位置.
3.答案全部在答题卡上完成,答在本试卷上无效.
4.考试结束后,将本试卷与答题卡一并交回.
第Ⅰ卷 选择题(共30分)
一、选择题(本大题共10小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑.)
1.在2024年,科技发展迅速,人工智能和大数据在各个领域都得到了广泛的应用,同时2024年人们的环境保护意识也得到了提高,可再生能源的使用更加广泛.的相反数是( ).
A. B. C. D.2024
2.下列运算正确的是( ).
A. B. C. D.
3.国家电影局2月18日发布数据,我国2024年春节档电影票房达80.16亿元,创造了新的春节档票房纪录,观影人次为1.63亿.将数据80.16亿用科学记数法表示为( ).
A. B. C. D.
4.中国代表团在杭州亚运会共收获201金、111银、71铜,总计383枚奖牌,创历史纪录.图①是2023年10月2日乒乓球男单颁奖现场.图②是领奖台的示意图,则此领奖台的主视图是( ).
图① 图②
A.B.C.D.
5.不等式组的解集在数轴上表示为( ).
A.B.C.D.
6.为了方便市民绿色出行,太原市推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,,.当为( )度时,AM与CB平行( ).
A.16 B.60 C.66 D.114
7.已知当时,分式无意义;当时,此分式的值为0,则的值是( ).
A. B. C. D.
8.一个不透明的口袋里装有分别标有汉字“大”、“美”、“山”、“西”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.从中任取一球,不放回,再从中任取一球,取出的两个球上的汉字能组成“美西”的概率是( ).
A. B. C. D.
9.明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”(一种水利灌溉工具)的工作原理.如图2,筒车盛水桶的运行轨道是以轴心O为圆心的圆.已知圆心O在水面上方,且被水面截得弦AB长为8米,半径长为6米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( ).
图1 图2
A.2米 B.4米 C.米 D.米
10.题目:“如图,已知抛物线,点是y轴上的一点,将点M向右平移5个单位长度得到点N,若线段MN与L只有一个公共点,直接写出n的取值范围.”对于其答案,甲答:,乙答:,丙答:,丁答:,则下列说法正确的是( ).
A.只有甲答的对 B.甲、乙答案合在一起才完整
C.甲、丙答案合在一起才完整 D.甲、丁答案合在一起才完整
第Ⅱ卷 非选择题(共90分)
二、填空题(本大题共5个小题,每小题3分,共15分)
11.在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式因式分解的结果是,若取,时,则各个因式的值是:,,,把这些值从小到大排列得到016128,于是就可以把“016128”作为一个六位数的密码,对于多项式,取,时,请你写出用上述方法产生的密码__________.
12.2023年11月20日,“第40届太原双塔牡丹文化节”精彩集锦登上美国纽约时代广场大屏,国色牡丹“走”向世界,锦绣太原“火”遍全球.在公园内,牡丹按正方形形状种植,在它的周围种植芍药,如图反映了牡丹的列数(n)和芍药的数量规律,那么当时,芍药的数量为__________株.
……
13.在两个不透明的袋子中分别装有一些除颜色外完全相同的球.甲袋中装有2个白球、1个黄球,乙袋中装有1个白球、2个黄球,这些球除颜色外无其他差别,在看不到球的情况下,从两个袋子中各随机摸出一个球,摸出的两个球的颜色都是白色的概率是__________.
14.如图,在一坡度的斜面上,一木箱沿斜面向上推进了10米,则木箱升高了__________米.
15.如图,在平面直角坐标系中,正方形ABCD的边长为4,,则点C的坐标为__________.
三、解答题(本大题共8个小题,共75分.解答应写出文字说明、证明过程或演算步骤.)
16.(本题共2个小题,每小题4分,共8分)
(1)计算:;
(2)解方程组:.
17.(本题8分)
如图,一次函数的图象与反比例函数的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知点A坐标为,点B的坐标为.
(1)求反比例函数的解析式和一次函数的解析式;
(2)连接OA,OB,求的面积;
(3)观察图象直接写出时,x的取值范围是__________.
18.(本题8分)
2023年10月10日,《2023年度中国精神心理健康》蓝皮书发布.中学生心理健康受到社会的广泛关注,某校开展心理健康教育专题讲座,就学生对心理健康知识的了解程度,采用随机抽样调查的方式,根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
扇形统计图 条形统计图
(1)接受问卷调查的学生共有__________人,条形统计图中m的值为__________,扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为__________;
(2)若该校共有学生800人,根据上述调查结果,可以估计出该校学生中对心理健康知识“不了解”的总人数为__________人;
(3)若某班要从对心理健康知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加心理健康知识竞赛;请用列表或画树状图的方法,求恰好抽到2名女生的概率.
19.(本题9分)阅读与思考:
【阅读材料】如图1,点A是外一点,点P是上一动点.若的半径为3,OA长度为5,则根据:,得到点P到点A的最短距离为:.
解决问题:
(1)如图2,已知正方形ABCD的边长为4,点M,N分别从点B,C同时出发,以相同的速度沿边BC,CD方向向终点C和D运动,连接AM和BN交于点P.
①证明:≌;
②求点P到点C的最短距离.
图1 图2 图3
(2)如图3,在平面直角坐标系中,等边的边OB在x轴正半轴上,点,,点D从点B出发,沿BO运动到点O,点E同时从点O以相同的速度出发,沿OA运动到点A,连接AD,BE,交点为点F,点M是y轴上一点,直接写出FM的最小值.
20.(本题9分)
“畅游山西,逛代县边靖楼”成为今年山西旅游新特色.某数学兴趣小组用无人机测量边靖楼AB的高度,测量方案如图:在坡底D处测得塔顶A的仰角为,沿坡比为的斜坡CD前行26米到达平台C处,在C处测得塔顶A的仰角为.
(1)求坡顶C到地面的距离;
(2)计算边靖楼AB的高度.
21.(本题9分)
2023年11月28日,2023龙芯产品发布暨用户大会举行.芯片目前是全球紧缺资源,某市政府通过招商引进“芯屏汽合、集终生智”等优势产业,发展新兴产业,某芯片公司引进了一条内存芯片生产线,开工第一季度生产300万个,第三季度生产432万个.试回答下列问题:
(1)已知每季度生产量的平均增长率相等,求前三季度生产量的平均增长率;
(2)经调查发现,1条生产线最大产能是600万个/季度,若每增加1条生产线,每条生产线的最大产能将减少20万个/季度,现该公司要保证每季度生产内存芯片2600万个,在增加产能同时又要节省投入成本的条件下(生产线越多,投入成本越大),应该再增加几条生产线?
22.(本题11分)综合与实践:
【问题情境】某数学兴趣小组在学完《平行四边形》之后,研究了新人教版数学教材第64页的数学活动1.其内容如下:
如果我们身旁没有量角器或三角尺,又需要作,,等大小的角,可以采用下面的方法(如图1); (1)对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平. (2)再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM.同时,得到了线段BN.
【知识运用】请根据上述过程完成下列问题:
图1 图2
(1)已知矩形纸片ABCD,,.求线段BM的长;
(2)通过观察猜测的度数是多少?并进行证明;
【综合提升】
(3)乐乐在探究活动的第(2)步基础上再次动手操作(如图2),将MN延长交BC于点G.将沿MG折叠,点B刚好落在AD边上点H处,连接GH,把纸片再次展平.请判断四边形BGHM的形状,并说明理由.
23.(本题13分)综合与探究:
如图,在平面直角坐标系中,抛物线与x轴交于点和点C,与y轴交于点,点P是抛物线上点A与点C之间的动点(不包括点A,点C).
备用图
(1)求抛物线的解析式;
(2)动点P在抛物线上,且在直线AB上方,求面积的最大值及此时点P的坐标;
(3)在(2)的条件下,将该抛物线向右平移2.5个单位,点F为点P的对应点,平移后的抛物线与y轴交于点E,Q为平移后的抛物线的对称轴上任意一点.若是以QE为腰的等腰三角形.求出所有符合条件的点Q的坐标.
2024年山西省初中学业水平测试信息卷
数学参考答案
一、(每小题3分,共30分)
1 2 3 4 5 6 7 8 9 10
D B C A B C B C C B
二、(每小题3分,共15分)
11.111213 12.80 13. 14.5 15、
三、(本大题共8个小题,共75分)
16.(1)解:原式
.(4分)
(2)解:
①×2+②,得,解得:,
把代入①,得,解得:,
所以方程组的解是.(8分)
17.解:(1)∵函数经过,∴,,
∴反比例函数的解析式是.(1分)
经过点,则,∴.
∵一次函数的图象经过点,点,
∴,解得,
∴一次函数的解析式为.(3分)
(2)一次函数,
当时,,∴,,
∴的面积.(6分)
(3)反比例函数与一次函数交于,,
∴时x的取值范围是或.(8分)
18.解:(1)∵基本了解的有40人,占50%,
∴接受问卷调查的学生共有%=80(人),
条形统计图中m的值为:,
扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为:.
故答案为:80,16,.(3分)
(2)可以估计出该校学生中对心理健康知识“不了解”的总人数为:(人).
故答案为:40.(4分)
(3)画树状图如下:
一共有12种等可能的结果,其中恰好抽到2名女生的结果有2种,
∴P(恰好抽到2名女生).(8分)
19.(1)①证明:由题可知,
∵,,∴≌(SAS).(2分)
②解:∵≌,∴,(3分)
∵,∴,
∴,
∴P点在以AB为直径的圆上.(4分)
取AB的中点O,连接OP,PC,OC,
∴,(5分)
又∵,,
∴,(6分)
∴PC的最短距离是.(7分)
(2)(9分)
提示:
20.解:(1)延长AB交PQ于点E,过点C作,垂足为点F,
则,,
设米,则米,
在中,米,
∴,∴,
解得,(负值舍去),
∴米,米,
即坡顶C到地面的距离为10米.(4分)
(2)设米,
在中,,
∴,;
在中,,,
∴,
∴,∴,解得,
∴米,
即边靖楼AB的高度为米.(9分)
21.解:(1)设前三季度生产量的平均增长率为x,
依题意得:,(2分)
解得:%,(不符合题意,舍去),
答:前三季度生产量的平均增长率为20%.(4分)
(2)设应该再增加m条生产线,
则每条生产线的最大产能为万个/季度,
依题意得:,(6分)
整理得:,
解得:,,(7分)
又∵在增加产能同时又要节省投入成本,
∴.(8分)
答:应该再增加4条生产线.(9分)
22.解:(1)∵四边形ABCD为矩形,∴,
∵,,∴.(2分)
(2)猜测:,
证明:连接AN,如图:
∵EF为折痕,∴EF垂直平分AB,∴,
∵由折叠所得,∴,
∴,则为等边三角形,
∴,∴.(7分)
(3)四边形BGHM为菱形,理由:
由题易得,BN平分,∴,
由折叠可得,∴,
又∵,∴四边形BGHM是平行四边形,
∴四边形BGHM是菱形.(11分)
23.解:(1)由抛物线经过,得:
,解得:,
∴抛物线的解析式为:.(2分)
(2)设直线AB的解析式为,
经过,得:,解得:,
∴直线AB的解析式为,
过点P作x轴的垂线交AB于点H,
设,,
则,
则面积,
即,
∴当时,面积最大值为,
此时.(7分)
(3),
则平移后的抛物线表达式为:,则点,
当时,,则点,设点,
由点Q,E,F的坐标得,
,,,
当时,则,解得:,
则点Q的坐标为:.
当时,则,解得:,
则点Q的坐标为:,
检验得点Q,点E,点F三点不共线.
综上,点Q的坐标为:或或.(13分)
同课章节目录
