15.1.1从分数到分式 课件(共21张PPT) 初中数学人教版八年级上册
文档属性
| 名称 | 15.1.1从分数到分式 课件(共21张PPT) 初中数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 16.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
15.1.1从分数到分式
第十五章——分式
能熟练地求出分式有意义、无意义及分式值为零的条件.
理解分式的概念;
01
02
学习目标
新知导入
阅读本章引言部分的问题,一艘轮船在静水中的最大航速是30km/h,它以最大船速沿江顺流航行90km所用时间,与以最大航速逆流航行60千米所用的时间相等.江水的流速是多少
如果设江水的流速为 v km/h.
以最大船速顺流航行90千米所用时间
以最大航速逆流航行60千米所用的时间
探究新知
(1)长方形的面积为10 cm ,长为 7 cm,则宽为_____cm;长方形的面积为S,长为a,则宽为_____.
(2)把体积为200 cm 的水倒入底面积为 33 cm 的圆柱形容器中,则水面高度为_____cm;把体积为V 的水倒入底面积为S的圆柱形容器中,则水面高度为____.
探究新知
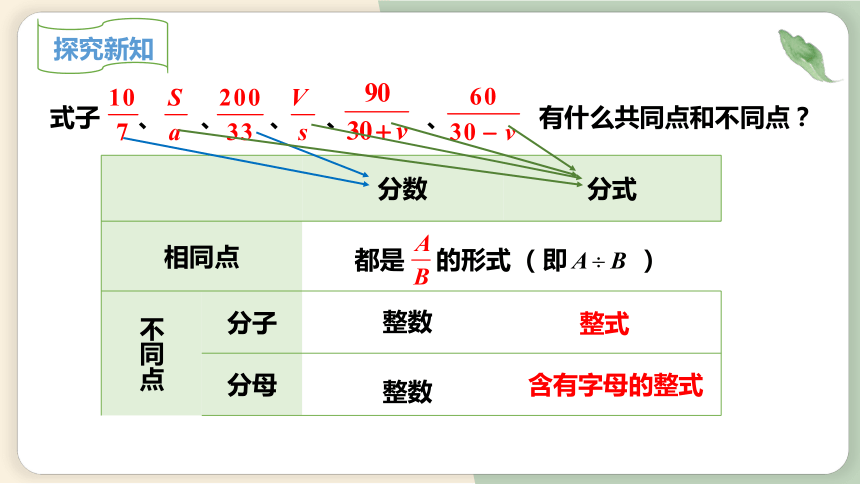
式子 、 、 、 、 、 有什么共同点和不同点?
分数 分式
相同点 不同点 分子
分母
都是 的形式 (即 )
整数
整数
整式
含有字母的整式
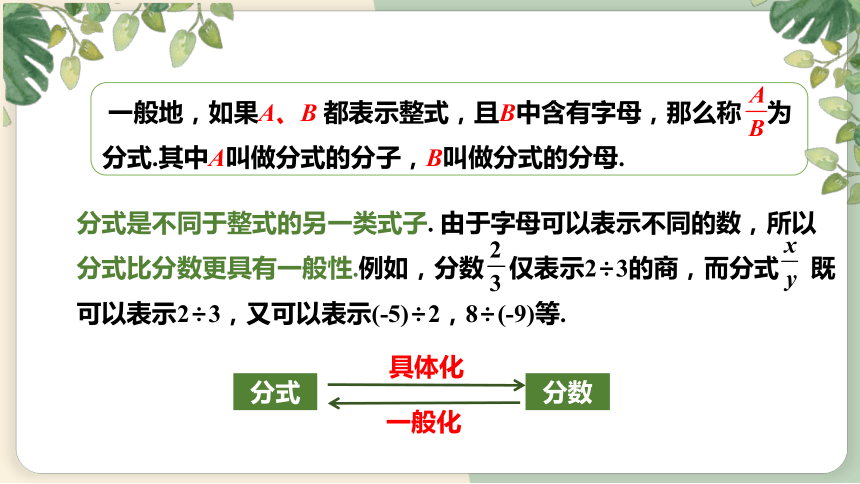
一般地,如果A、B 都表示整式,且B中含有字母,那么称 为分式.其中A叫做分式的分子,B叫做分式的分母.
分式是不同于整式的另一类式子. 由于字母可以表示不同的数,所以分式比分数更具有一般性.例如,分数 仅表示2÷3的商,而分式 既可以表示2÷3,又可以表示(-5)÷2,8÷(-9)等.
分数
分式
具体化
一般化
应用新知
下列各式哪些是整式?哪些是分式?
整式
整式
分式
整式
分式
分式
分式
分式
整式
1.判断时,注意含有π的式子,π是常数.
2.式子中含有多项时,若其中有一项分母含有字母,则该式也为分式,如:
3.判断时,不用化简只看形式,如
区分整式与分式的标准就是看分母中是否含有字母,含有字母的是分式,不含字母的是整式.
总结:
探究新知
【思考】要使分数有意义,分数中的分母不能为0.要使分式有意义,分式中的分母应满足什么条件?
分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B≠0时,分式 才有意义.
除数
探究新知
【思考】分式 的值为零,分式的分子和分母应满足什么条件?
分式的值是在分式有意义的前提下才可以考虑的,所以使分式 的值为0的条件是 A=0且 B≠0,二者缺一不可.
对于分式 :
当_______时,分式有意义;
当_______时,分式无意义;
当 时,分式值为0.
B≠0
B=0
B≠0,A=0
总结:
例题练习
下列分式中的字母满足什么条件时分式有意义?
(1) (2) (3) (4)
解:
(1)要使分式 有意义,则分母 3x≠0,即x ≠0.
(2)要使分式 有意义,则分母 x-1≠0,即x ≠1.
(3)要使分式 有意义,则分母 5-3b≠0,即 .
(4)要使分式 有意义,则分母x-y ≠ 0,即 x ≠ y.
B
B
A
小结
对于分式 :
当_______时,分式有意义;
当_______时,分式无意义;
当 时,分式值为0.
B≠0
B=0
B≠0,A=0
一般地,如果A、B都表示整式,且B中含有字母,那么称 为分式.其中A叫做分式的分子,B叫做分式的分母.
谢谢观看
15.1.1从分数到分式
第十五章——分式
能熟练地求出分式有意义、无意义及分式值为零的条件.
理解分式的概念;
01
02
学习目标
新知导入
阅读本章引言部分的问题,一艘轮船在静水中的最大航速是30km/h,它以最大船速沿江顺流航行90km所用时间,与以最大航速逆流航行60千米所用的时间相等.江水的流速是多少
如果设江水的流速为 v km/h.
以最大船速顺流航行90千米所用时间
以最大航速逆流航行60千米所用的时间
探究新知
(1)长方形的面积为10 cm ,长为 7 cm,则宽为_____cm;长方形的面积为S,长为a,则宽为_____.
(2)把体积为200 cm 的水倒入底面积为 33 cm 的圆柱形容器中,则水面高度为_____cm;把体积为V 的水倒入底面积为S的圆柱形容器中,则水面高度为____.
探究新知
式子 、 、 、 、 、 有什么共同点和不同点?
分数 分式
相同点 不同点 分子
分母
都是 的形式 (即 )
整数
整数
整式
含有字母的整式
一般地,如果A、B 都表示整式,且B中含有字母,那么称 为分式.其中A叫做分式的分子,B叫做分式的分母.
分式是不同于整式的另一类式子. 由于字母可以表示不同的数,所以分式比分数更具有一般性.例如,分数 仅表示2÷3的商,而分式 既可以表示2÷3,又可以表示(-5)÷2,8÷(-9)等.
分数
分式
具体化
一般化
应用新知
下列各式哪些是整式?哪些是分式?
整式
整式
分式
整式
分式
分式
分式
分式
整式
1.判断时,注意含有π的式子,π是常数.
2.式子中含有多项时,若其中有一项分母含有字母,则该式也为分式,如:
3.判断时,不用化简只看形式,如
区分整式与分式的标准就是看分母中是否含有字母,含有字母的是分式,不含字母的是整式.
总结:
探究新知
【思考】要使分数有意义,分数中的分母不能为0.要使分式有意义,分式中的分母应满足什么条件?
分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B≠0时,分式 才有意义.
除数
探究新知
【思考】分式 的值为零,分式的分子和分母应满足什么条件?
分式的值是在分式有意义的前提下才可以考虑的,所以使分式 的值为0的条件是 A=0且 B≠0,二者缺一不可.
对于分式 :
当_______时,分式有意义;
当_______时,分式无意义;
当 时,分式值为0.
B≠0
B=0
B≠0,A=0
总结:
例题练习
下列分式中的字母满足什么条件时分式有意义?
(1) (2) (3) (4)
解:
(1)要使分式 有意义,则分母 3x≠0,即x ≠0.
(2)要使分式 有意义,则分母 x-1≠0,即x ≠1.
(3)要使分式 有意义,则分母 5-3b≠0,即 .
(4)要使分式 有意义,则分母x-y ≠ 0,即 x ≠ y.
B
B
A
小结
对于分式 :
当_______时,分式有意义;
当_______时,分式无意义;
当 时,分式值为0.
B≠0
B=0
B≠0,A=0
一般地,如果A、B都表示整式,且B中含有字母,那么称 为分式.其中A叫做分式的分子,B叫做分式的分母.
谢谢观看
