15.3分式方程(第二课时) 课件(共26张PPT) 初中数学人教版八年级上册
文档属性
| 名称 | 15.3分式方程(第二课时) 课件(共26张PPT) 初中数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-11 21:33:25 | ||
图片预览








文档简介
(共26张PPT)
15.3分式方程
(第二课时)
第十五章——分式
能根据题意找出正确的等量关系,列出分式方程并求解,会根据实际意义验证结果是否合理.
会列分式方程解决实际问题;
01
02
学习目标
知识回顾
上节课我们学习了分式方程及其解法:
解分式方程的一般步骤.
(1)在方程的两边都乘以最简公分母,约去分母,化成整式方程;
(2)解这个整式方程;
(3)把整式方程的根代入最简公分母,看结果是不是为零,使最简公分母为零的根是原方程的增根,必须舍去;
(4)写出原方程的根.
分母中含未知数的方程叫做分式方程.
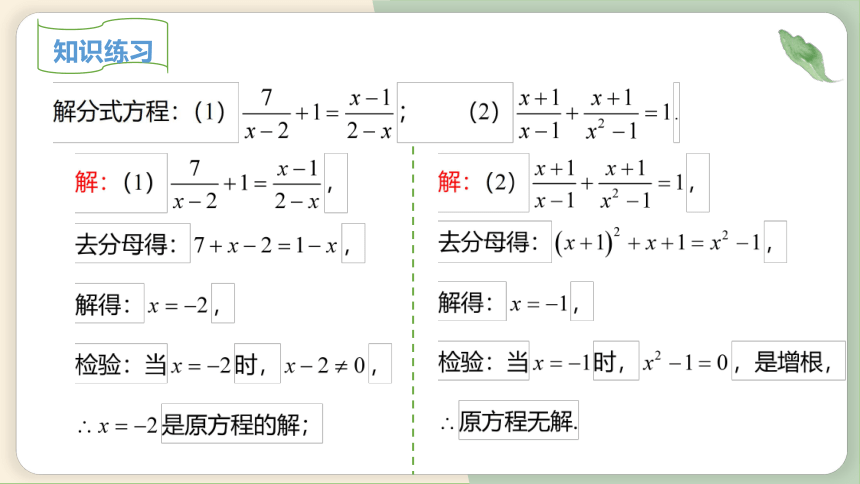
知识练习
新知导入
【问题1】两个工程队共同参与一项筑路工程,甲队单独施工 1 个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
尝试利用分式方程解决该问题
探究新知
工作总量=工作效率×工作时间
【分析】甲队1个月完成总工程的_____,设乙队单独施工1个月能完成总工程的 ,那么甲队半个月完成总工程的____,乙队半个月完成总工程____,两队半个月完成总工程的 .
【问题1】两个工程队共同参与一项筑路工程,甲队单独施工 1 个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
探究新知
找等量关系
甲队施工1个月的工程量 + 甲队施工半个月的工程量 + 乙队施工半个月的工程量 = 总工程量(记为1).
【问题1】两个工程队共同参与一项筑路工程,甲队单独施工 1 个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
+
+
探究新知
解:设乙队单独施工1个月能完成总工程的 ,记总工程量为1,
根据工程的实际进度,得 .
方程两边同时乘以6x,得 2x+x+3=6x .解得 x=1.
检验:当x=1时,6x≠0.
所以原分式方程的解为 x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队的施工速度快.
甲队施工1个月的工程量 + 甲队施工半个月的工程量 + 乙队施工半个月的工程量 = 总工程量(记为1).
探究新知
【问题2】某次列车平均提速 v km/h.用相同的时间,列车提速前行驶 s km,提速后比提速前多行驶 50 km,提速前列车的平均速度为多少?
行程问题:路程 = 速度×时间
【分析】这里的字母 v,s表示已知数据,设提速前列车的平均速度为 x km/h,那么提速前列车行驶 s km所用时间为_______h,提速后列车的平均速度为_______ km/h,提速后列车运行(s+50)km所用时间为_______h.
探究新知
找等量关系
提速后的行驶时间 = 提速前的行驶时间
【问题2】某次列车平均提速 v km/h.用相同的时间,列车提速前行驶 s km,提速后比提速前多行驶 50 km,提速前列车的平均速度为多少?
探究新知
提速后的行驶时间 = 提速前的行驶时间
解:根据行驶时间的等量关系,得
=
方程两边同乘 ,得
=
去括号,得
解得 x = .
检验:由于 v,s 都是正数,当x = 时;x(x+v)≠0,
所以,x = 是原分式方程的解,且符合题意.
答:提速前列车的平均速度为 km/h.
审:审清题意,找出题中的相等关系,分清题中的已知量、未知量;
设:设出恰当的未知数,注意单位和语言的完整性;
列:根据题中的相等关系,正确列出分式方程;
解:解所列分式方程;
验:既要检验所得的解是否为所列分式方程的解,又要检验所得的解是否符合实际问题的要求;
答:写出答案.
列分式方程解决实际问题的一般步骤
D
B
D
小结
审
设
列
解
验
答
设:_______
未知数
解:_______
列:_________
检验:1.__________________;
2.______________
分式方程
分式方程
是否是分式方程的解
是否符合题意
谢谢观看
15.3分式方程
(第二课时)
第十五章——分式
能根据题意找出正确的等量关系,列出分式方程并求解,会根据实际意义验证结果是否合理.
会列分式方程解决实际问题;
01
02
学习目标
知识回顾
上节课我们学习了分式方程及其解法:
解分式方程的一般步骤.
(1)在方程的两边都乘以最简公分母,约去分母,化成整式方程;
(2)解这个整式方程;
(3)把整式方程的根代入最简公分母,看结果是不是为零,使最简公分母为零的根是原方程的增根,必须舍去;
(4)写出原方程的根.
分母中含未知数的方程叫做分式方程.
知识练习
新知导入
【问题1】两个工程队共同参与一项筑路工程,甲队单独施工 1 个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
尝试利用分式方程解决该问题
探究新知
工作总量=工作效率×工作时间
【分析】甲队1个月完成总工程的_____,设乙队单独施工1个月能完成总工程的 ,那么甲队半个月完成总工程的____,乙队半个月完成总工程____,两队半个月完成总工程的 .
【问题1】两个工程队共同参与一项筑路工程,甲队单独施工 1 个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
探究新知
找等量关系
甲队施工1个月的工程量 + 甲队施工半个月的工程量 + 乙队施工半个月的工程量 = 总工程量(记为1).
【问题1】两个工程队共同参与一项筑路工程,甲队单独施工 1 个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
+
+
探究新知
解:设乙队单独施工1个月能完成总工程的 ,记总工程量为1,
根据工程的实际进度,得 .
方程两边同时乘以6x,得 2x+x+3=6x .解得 x=1.
检验:当x=1时,6x≠0.
所以原分式方程的解为 x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队的施工速度快.
甲队施工1个月的工程量 + 甲队施工半个月的工程量 + 乙队施工半个月的工程量 = 总工程量(记为1).
探究新知
【问题2】某次列车平均提速 v km/h.用相同的时间,列车提速前行驶 s km,提速后比提速前多行驶 50 km,提速前列车的平均速度为多少?
行程问题:路程 = 速度×时间
【分析】这里的字母 v,s表示已知数据,设提速前列车的平均速度为 x km/h,那么提速前列车行驶 s km所用时间为_______h,提速后列车的平均速度为_______ km/h,提速后列车运行(s+50)km所用时间为_______h.
探究新知
找等量关系
提速后的行驶时间 = 提速前的行驶时间
【问题2】某次列车平均提速 v km/h.用相同的时间,列车提速前行驶 s km,提速后比提速前多行驶 50 km,提速前列车的平均速度为多少?
探究新知
提速后的行驶时间 = 提速前的行驶时间
解:根据行驶时间的等量关系,得
=
方程两边同乘 ,得
=
去括号,得
解得 x = .
检验:由于 v,s 都是正数,当x = 时;x(x+v)≠0,
所以,x = 是原分式方程的解,且符合题意.
答:提速前列车的平均速度为 km/h.
审:审清题意,找出题中的相等关系,分清题中的已知量、未知量;
设:设出恰当的未知数,注意单位和语言的完整性;
列:根据题中的相等关系,正确列出分式方程;
解:解所列分式方程;
验:既要检验所得的解是否为所列分式方程的解,又要检验所得的解是否符合实际问题的要求;
答:写出答案.
列分式方程解决实际问题的一般步骤
D
B
D
小结
审
设
列
解
验
答
设:_______
未知数
解:_______
列:_________
检验:1.__________________;
2.______________
分式方程
分式方程
是否是分式方程的解
是否符合题意
谢谢观看
