11.1.1 三角形的边 课件(共24张PPT)
文档属性
| 名称 | 11.1.1 三角形的边 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-12 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
第11章 与三角形有关的线段
11.1.1 三角形的边
导入新课-讲授新课-课堂练习-课堂小结
学习目标
1.了解三角形的相关概念,会按边对三角形进行分类。(抽象能力)
2.掌握三角形的三边关系,会运用三角形的三边关系解决问题。
生活链接
这些都是生活中常见的三角形
知识点一
三角形及相关概念
1.三角形的概念
由不在同一条直线上的三条线段首位顺次所组成的图形叫做三角形。
巧学巧记
巧记三角形定义
三条线段不共线,
首尾相接是关键。
线段即为三条边,
公共端点为顶点。
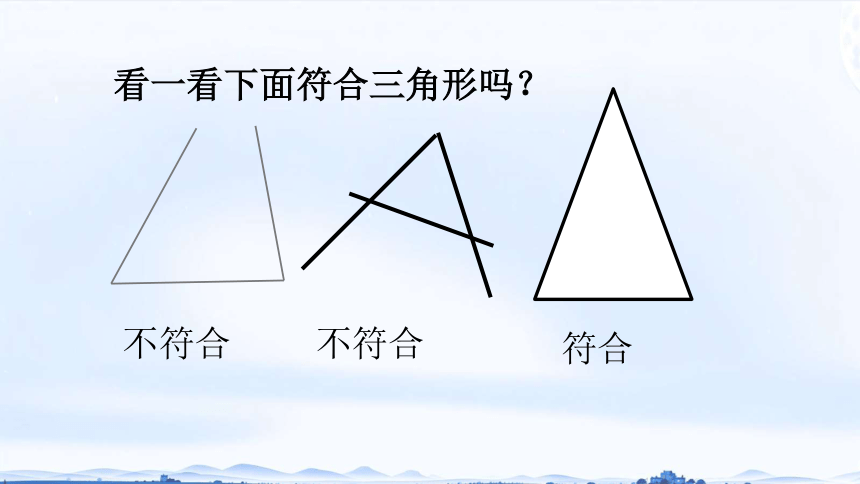
看一看下面符合三角形吗?
不符合
不符合
符合
2.三角形的三要素
(
(
(
B
A
C
α
b
c
角
:相邻两边组成三角形的内角,简称三角形的角。
顶点
边
:相邻两边的公共端点是三角形的顶点。
:组成三角形的线段叫做三角形的边。
如图:△ABC有三条边,三个内角,三个顶点。
3.三角形的表示
顶点A,B,C的三角形,记作“△ABC”,读作“三角形ABC”。
注意:在△ABC中,∠A的对边可以用BC表示,也可以用a表示;∠B对边可以用AC表示,也可以用b表示;∠C的对边可以用AB表示,也可以用c表示。
如图所示,图中有几个三角形?用符号表示出这些三角形,并写出它们的边和角。
A
B
C
D
解:图中有三个三角形,分别是△ABC,△ABD,△ADC.
△ABC的三边分别是线段AB,BC,AC,三个内角分别是∠BAC,∠B,∠C;
△ABD的三边分别是线段AB,BD,AD,三个内角分别是∠BAD,∠B,∠ADB;
△ADC的三边分别是线段AD,DC,AC,三个内角分别是∠ADC,∠DAC,∠C.
知识点二
1.特殊的三角形
三角形的分类
(1)等腰三角形:有两条边相等三角形,如图.
A
B
C
底边
腰
腰
(
顶角
(
底角
(
底角
(2)等边三角形:三边都相等的三角形.
2.三角形的分类
(1)文字语言
按角分类:三角形分为锐角三角形、直角三角形、钝角三角形.
(2)图示
三边都不相等的三角形
等腰三角形
等边三角形
直角三角形
钝角三角形
锐角三角形
若△ABC的三边长a,b,c满足(α-b)+|b-c|=0,则△ABC的形状是
练一练
A.钝角三角形
B.直角三角形
C.等边三角形
D.以上均不正确
解析:根据非负数的性质,得α-b=0,b-c=0,所以α=b,b=c,所以△ABC是等边三角形.故选C
(C)
知识点三
三角形的三边关系
三边关系
(1)文字语言:三角形两边的和大于第三边
符号语言:α+b>c,b+c>α,α+c>b
应用:判断三条线段能否成三角形;
(2)文字语言:三角形两边的差小于第三边
符号语言:|α-b|应用:已知两边长,求第三边长的取值范围;
若一个三角形的两边长分别是2和4,第三边的长可能是( )
当堂练习
A.2
B.4
C.6
D.8
解析:设第三边的长为x,由三角形的三边关系,得4-2<ⅹ<4+2,即2<ⅹ<6.观察四个选项,知B项正确.
B
特别提醒
“两边的和”“两边的差”中的“两边”是指三角形的任意两边。
总结
根据三角形的三边关系可得三角形的任意一边总是大于另两边之差,小于另两边之和,据此通过列不等式(组)求出三角形的待求边长的取值范围.
巩固练习
1.已知一个三角形的两边长分别是3和7,且第三边的长是整数,这个三角形的周长的最小值是多少?
解:设第三边的长为x,由三角形的三边关系,得7-32.下列长度的三条线段能组成三角形的是( )
A.2,2,4
B.5,6,12
C.5,7,2
D.6,8,10
思路分析:根据“三角形两边之和大于第三边”可以判断长度为各个选项中数值的三条线段是否能组成三角形。
D
3.若一个等腰三角形中的两边长分别是4cm和8cm,则此三角形的周长为( )
A.16cm
B.20cm
C.16cm或20cm
解析:当腰长是4cm时,则三角形的三边长分别是4cm,4cm,8cm,4+4=8,不满足三角形的三边关系,舍去;当腰长是8cm时,三角形的三边长分别是8cm,8cm,4cm,8+4>8,符合三角形的三边关系,此时三角形的周长是20cm.
B
4.如图,三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
D
5.在△ABC中,AB=10,BC=1,并且AC的长为偶数,则△ABC的周长为( )
A.20 B.21 C.22 D.23
B.
6.已知α,b,c是△ABC的三边长,化简lα-b-cl+lb-c-αl+Ⅰc+α-bl.
解:因为α-(b+c)<0,b-(c+a)<0,c+a-b>0,所以lα-b-cl+lb-c-αl+lc+α-bl
=lα-(b+c)l+lb-(c+α)Ⅰ+lc+α-bl
=(b+c)-α+(c+α)-b+c+α-b
=α-b+3c
知识梳理
谢谢观看
第11章 与三角形有关的线段
11.1.1 三角形的边
导入新课-讲授新课-课堂练习-课堂小结
学习目标
1.了解三角形的相关概念,会按边对三角形进行分类。(抽象能力)
2.掌握三角形的三边关系,会运用三角形的三边关系解决问题。
生活链接
这些都是生活中常见的三角形
知识点一
三角形及相关概念
1.三角形的概念
由不在同一条直线上的三条线段首位顺次所组成的图形叫做三角形。
巧学巧记
巧记三角形定义
三条线段不共线,
首尾相接是关键。
线段即为三条边,
公共端点为顶点。
看一看下面符合三角形吗?
不符合
不符合
符合
2.三角形的三要素
(
(
(
B
A
C
α
b
c
角
:相邻两边组成三角形的内角,简称三角形的角。
顶点
边
:相邻两边的公共端点是三角形的顶点。
:组成三角形的线段叫做三角形的边。
如图:△ABC有三条边,三个内角,三个顶点。
3.三角形的表示
顶点A,B,C的三角形,记作“△ABC”,读作“三角形ABC”。
注意:在△ABC中,∠A的对边可以用BC表示,也可以用a表示;∠B对边可以用AC表示,也可以用b表示;∠C的对边可以用AB表示,也可以用c表示。
如图所示,图中有几个三角形?用符号表示出这些三角形,并写出它们的边和角。
A
B
C
D
解:图中有三个三角形,分别是△ABC,△ABD,△ADC.
△ABC的三边分别是线段AB,BC,AC,三个内角分别是∠BAC,∠B,∠C;
△ABD的三边分别是线段AB,BD,AD,三个内角分别是∠BAD,∠B,∠ADB;
△ADC的三边分别是线段AD,DC,AC,三个内角分别是∠ADC,∠DAC,∠C.
知识点二
1.特殊的三角形
三角形的分类
(1)等腰三角形:有两条边相等三角形,如图.
A
B
C
底边
腰
腰
(
顶角
(
底角
(
底角
(2)等边三角形:三边都相等的三角形.
2.三角形的分类
(1)文字语言
按角分类:三角形分为锐角三角形、直角三角形、钝角三角形.
(2)图示
三边都不相等的三角形
等腰三角形
等边三角形
直角三角形
钝角三角形
锐角三角形
若△ABC的三边长a,b,c满足(α-b)+|b-c|=0,则△ABC的形状是
练一练
A.钝角三角形
B.直角三角形
C.等边三角形
D.以上均不正确
解析:根据非负数的性质,得α-b=0,b-c=0,所以α=b,b=c,所以△ABC是等边三角形.故选C
(C)
知识点三
三角形的三边关系
三边关系
(1)文字语言:三角形两边的和大于第三边
符号语言:α+b>c,b+c>α,α+c>b
应用:判断三条线段能否成三角形;
(2)文字语言:三角形两边的差小于第三边
符号语言:|α-b|
若一个三角形的两边长分别是2和4,第三边的长可能是( )
当堂练习
A.2
B.4
C.6
D.8
解析:设第三边的长为x,由三角形的三边关系,得4-2<ⅹ<4+2,即2<ⅹ<6.观察四个选项,知B项正确.
B
特别提醒
“两边的和”“两边的差”中的“两边”是指三角形的任意两边。
总结
根据三角形的三边关系可得三角形的任意一边总是大于另两边之差,小于另两边之和,据此通过列不等式(组)求出三角形的待求边长的取值范围.
巩固练习
1.已知一个三角形的两边长分别是3和7,且第三边的长是整数,这个三角形的周长的最小值是多少?
解:设第三边的长为x,由三角形的三边关系,得7-3
A.2,2,4
B.5,6,12
C.5,7,2
D.6,8,10
思路分析:根据“三角形两边之和大于第三边”可以判断长度为各个选项中数值的三条线段是否能组成三角形。
D
3.若一个等腰三角形中的两边长分别是4cm和8cm,则此三角形的周长为( )
A.16cm
B.20cm
C.16cm或20cm
解析:当腰长是4cm时,则三角形的三边长分别是4cm,4cm,8cm,4+4=8,不满足三角形的三边关系,舍去;当腰长是8cm时,三角形的三边长分别是8cm,8cm,4cm,8+4>8,符合三角形的三边关系,此时三角形的周长是20cm.
B
4.如图,三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
D
5.在△ABC中,AB=10,BC=1,并且AC的长为偶数,则△ABC的周长为( )
A.20 B.21 C.22 D.23
B.
6.已知α,b,c是△ABC的三边长,化简lα-b-cl+lb-c-αl+Ⅰc+α-bl.
解:因为α-(b+c)<0,b-(c+a)<0,c+a-b>0,所以lα-b-cl+lb-c-αl+lc+α-bl
=lα-(b+c)l+lb-(c+α)Ⅰ+lc+α-bl
=(b+c)-α+(c+α)-b+c+α-b
=α-b+3c
知识梳理
谢谢观看
