11.3.1 多边形课件
图片预览








文档简介
(共24张PPT)
人
新课标
数学
8年级/上
八年级数学·上 新课标 [人]
第十一章 三角形
学习新知
检测反馈
11.3.1 多边形
问题情景
学 习 新 知
中国第一奇村诸葛八卦村
美国国防部大楼——五角大楼
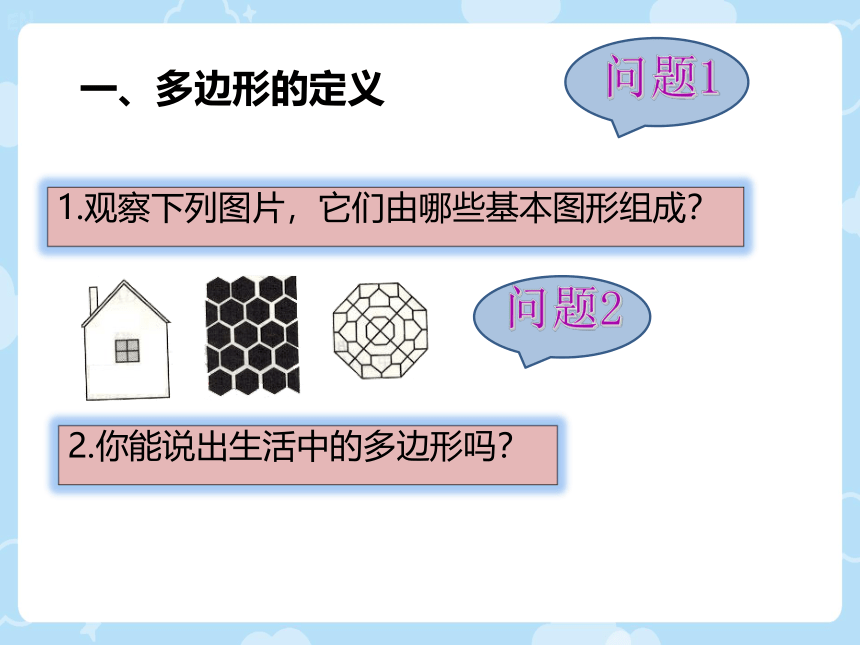
一、多边形的定义
1.观察下列图片,它们由哪些基本图形组成?
2.你能说出生活中的多边形吗?
问题1
问题2
总结
多边形:在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.按组成多边形线段的条数分为三角形、四边形、五边形……如果一个多边形由 条线段组成,这个多边形叫做 边形.
说 明
三角形中有三条线段,多边形中不止有三条线段,其定义中还加了一个条件:“在平面内”,这是因为三角形中的三个顶点肯定都在同一平面内,而四点、五点甚至更多的点就有可能在同一平面内,也有可能不在同一个平面内,而我们初中阶段主要探讨的是平面几何,所以应在前面加上条件:“ 在平面内”。
①在同一平面内;
②若干条线段;
③首尾顺次连接;
④封闭图形。
多边形定义的几个要素
二、多边形的相关概念
你能结合图1指出这个多边形的内角和外角吗?
小问题
∠A、∠B、∠BCD、∠D、∠E、∠F 是六边形的内角,∠DCM 是六边形的一个外角.
提醒
多边形相邻两边组成的角叫做多边形的内角,多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
连接多边形不相邻的两个顶点的线段叫做对角线,如图2所示,CF为对角线,那么从六边形的一个顶点出发可以得到几条对角线?那么六边形一共有多少条对角线呢?
小问题
知识拓展
1.多边形的有关问题,都是将多边形转化为三角形问题来解决的,体现了转化的思想方法。
2.从多边形的一个顶点引对角线时,这个顶点和相邻的两个顶点不能引对角线,那么还剩下(n-3)个顶点,就能引出(n-3)条对角线,从而得出结论:从n边形的一个顶点可引出(n-3)条对角线。
3.从一个顶点可以引出(n-3)条对角线,有n个顶点,共有n(n-3)条对角线,但每条对角线都重复两遍,所以n边
形对角线的条数为 。
你能说出下图中两个四边形的异同点吗?
思考
三、多边形的分类
图(1)中,画出四边形ABCD 的任何一条边所在的直线,整个四边形都在这条直线的同一侧;图(2)中,画出边CD 所在的直线,整个四边形不都在这条直线的同一侧.
总结
凸多边形:画出多边形的任何一条边所在的直线,如果整个多边形都在这条直线的同侧,那么这个多边形就是凸多边形.
凹多边形:画出多边形的某一条边所在的直线,如果整个多边形不在这条直线的同侧,那么这个多边形就是凹多边形.
四、认识正多边形
正方形的边长、角有什么特点,你能给正多边形下定义吗?
思考
总结
正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.
分析:正六边形的特点是有六个边,每条边相等.
解:因为正多边形的边长相等,
所以正六边形的六条边都相等,
所以每条边长为36÷6=6cm.
1.若一个正六边形的周长为36cm,请求出它的边长.
本题考查的是正多边形的性质,能够熟记正多边形的特征是解题关键.
解题策略
补充例题
解题策略
解:设多边形的边数为 n,
根据n边形过一个顶点有 (n-3) 条对角线,
所以 n-2=6,解得n=8,
它们把 n 边形分割成了 (n-2) 个三角形,
2.若一个多边形自一个顶点引对角线把它分割为六个三角形,则这个多边形的边数有几条?
解答此类问题可以运用对角线计算过程进行分析,也可以画图形进行考虑,明确对角线是不相邻顶点之间的线段,所以n边形由一个顶点出发可作(n-3)条对角线,即可分出(n-2)个三角形.
所以这个多边形是八边形.
1.多边形的定义、内角、外角、对角线等概念,n边形对角线的计算公式: ;
2. 多边形的分类;
3.正多边形的定义及其性质.
D
解析:根据外角的定义可知,外角是多边形的一边延长线与另一边所成的夹角,选项A中∠1是两边延长线的夹角,选项B 中∠1的一边不是多边形一边的延长线,选项C 中∠1是多边形的内角.
1.在下列图形中,∠1是多边形外角的是( )
检测反馈
解析:因为从n边形的一个顶点引对角线,最多可引(n-3)条,所以n-3=10,得n=13.
A
2.若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( )
A.十三边形 B.十二边形
C.十一边形 D.十边形
解析:因为从七边形的一个顶点出发会有4条对角线,共有7个顶点,所以共作28条对角线,由于重复,所以七边形共有14条对角线;或者利用公式求解.
D
3.七边形的对角线共有( )
A.42条 B.28条
C.21条 D.14条
解析:根据三角形的稳定性进行判定,所以从五边形的一个顶点出发作对角线即可.
4.要使五边形木架(用5根木条钉成)不变形,至少需要钉( )木条.
A . 1根 B.2根 C.3根 D.4根
B
解析:根据规律可知,从n边形的一个顶点引对角线可分割为(n-2)个三角形,所以n-2=5,得n=7.
5.过一个多边形的一个顶点的所有对角线把多边形分成5个三角形,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
C
谢 谢
人
新课标
数学
8年级/上
八年级数学·上 新课标 [人]
第十一章 三角形
学习新知
检测反馈
11.3.1 多边形
问题情景
学 习 新 知
中国第一奇村诸葛八卦村
美国国防部大楼——五角大楼
一、多边形的定义
1.观察下列图片,它们由哪些基本图形组成?
2.你能说出生活中的多边形吗?
问题1
问题2
总结
多边形:在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.按组成多边形线段的条数分为三角形、四边形、五边形……如果一个多边形由 条线段组成,这个多边形叫做 边形.
说 明
三角形中有三条线段,多边形中不止有三条线段,其定义中还加了一个条件:“在平面内”,这是因为三角形中的三个顶点肯定都在同一平面内,而四点、五点甚至更多的点就有可能在同一平面内,也有可能不在同一个平面内,而我们初中阶段主要探讨的是平面几何,所以应在前面加上条件:“ 在平面内”。
①在同一平面内;
②若干条线段;
③首尾顺次连接;
④封闭图形。
多边形定义的几个要素
二、多边形的相关概念
你能结合图1指出这个多边形的内角和外角吗?
小问题
∠A、∠B、∠BCD、∠D、∠E、∠F 是六边形的内角,∠DCM 是六边形的一个外角.
提醒
多边形相邻两边组成的角叫做多边形的内角,多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
连接多边形不相邻的两个顶点的线段叫做对角线,如图2所示,CF为对角线,那么从六边形的一个顶点出发可以得到几条对角线?那么六边形一共有多少条对角线呢?
小问题
知识拓展
1.多边形的有关问题,都是将多边形转化为三角形问题来解决的,体现了转化的思想方法。
2.从多边形的一个顶点引对角线时,这个顶点和相邻的两个顶点不能引对角线,那么还剩下(n-3)个顶点,就能引出(n-3)条对角线,从而得出结论:从n边形的一个顶点可引出(n-3)条对角线。
3.从一个顶点可以引出(n-3)条对角线,有n个顶点,共有n(n-3)条对角线,但每条对角线都重复两遍,所以n边
形对角线的条数为 。
你能说出下图中两个四边形的异同点吗?
思考
三、多边形的分类
图(1)中,画出四边形ABCD 的任何一条边所在的直线,整个四边形都在这条直线的同一侧;图(2)中,画出边CD 所在的直线,整个四边形不都在这条直线的同一侧.
总结
凸多边形:画出多边形的任何一条边所在的直线,如果整个多边形都在这条直线的同侧,那么这个多边形就是凸多边形.
凹多边形:画出多边形的某一条边所在的直线,如果整个多边形不在这条直线的同侧,那么这个多边形就是凹多边形.
四、认识正多边形
正方形的边长、角有什么特点,你能给正多边形下定义吗?
思考
总结
正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.
分析:正六边形的特点是有六个边,每条边相等.
解:因为正多边形的边长相等,
所以正六边形的六条边都相等,
所以每条边长为36÷6=6cm.
1.若一个正六边形的周长为36cm,请求出它的边长.
本题考查的是正多边形的性质,能够熟记正多边形的特征是解题关键.
解题策略
补充例题
解题策略
解:设多边形的边数为 n,
根据n边形过一个顶点有 (n-3) 条对角线,
所以 n-2=6,解得n=8,
它们把 n 边形分割成了 (n-2) 个三角形,
2.若一个多边形自一个顶点引对角线把它分割为六个三角形,则这个多边形的边数有几条?
解答此类问题可以运用对角线计算过程进行分析,也可以画图形进行考虑,明确对角线是不相邻顶点之间的线段,所以n边形由一个顶点出发可作(n-3)条对角线,即可分出(n-2)个三角形.
所以这个多边形是八边形.
1.多边形的定义、内角、外角、对角线等概念,n边形对角线的计算公式: ;
2. 多边形的分类;
3.正多边形的定义及其性质.
D
解析:根据外角的定义可知,外角是多边形的一边延长线与另一边所成的夹角,选项A中∠1是两边延长线的夹角,选项B 中∠1的一边不是多边形一边的延长线,选项C 中∠1是多边形的内角.
1.在下列图形中,∠1是多边形外角的是( )
检测反馈
解析:因为从n边形的一个顶点引对角线,最多可引(n-3)条,所以n-3=10,得n=13.
A
2.若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( )
A.十三边形 B.十二边形
C.十一边形 D.十边形
解析:因为从七边形的一个顶点出发会有4条对角线,共有7个顶点,所以共作28条对角线,由于重复,所以七边形共有14条对角线;或者利用公式求解.
D
3.七边形的对角线共有( )
A.42条 B.28条
C.21条 D.14条
解析:根据三角形的稳定性进行判定,所以从五边形的一个顶点出发作对角线即可.
4.要使五边形木架(用5根木条钉成)不变形,至少需要钉( )木条.
A . 1根 B.2根 C.3根 D.4根
B
解析:根据规律可知,从n边形的一个顶点引对角线可分割为(n-2)个三角形,所以n-2=5,得n=7.
5.过一个多边形的一个顶点的所有对角线把多边形分成5个三角形,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
C
谢 谢
