15.1.2 平移的特征 课件
图片预览


文档简介
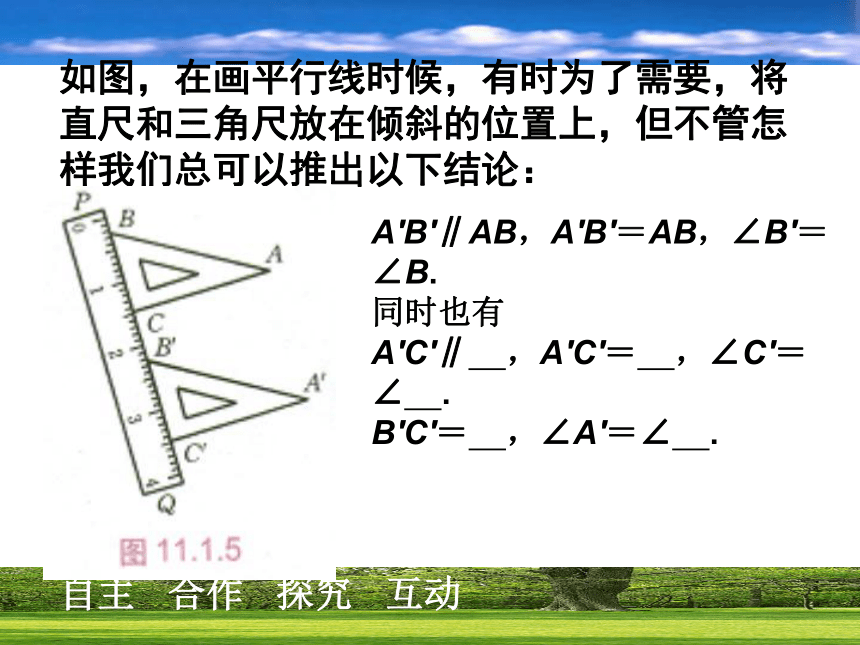
课件16张PPT。15.1.2平移的特征如图,在画平行线时候,有时为了需要,将直尺和三角尺放在倾斜的位置上,但不管怎样我们总可以推出以下结论: A′B′∥AB,A′B′=AB,∠B′=∠B.
同时也有
A′C′∥ ,A′C′= ,∠C′=∠ .
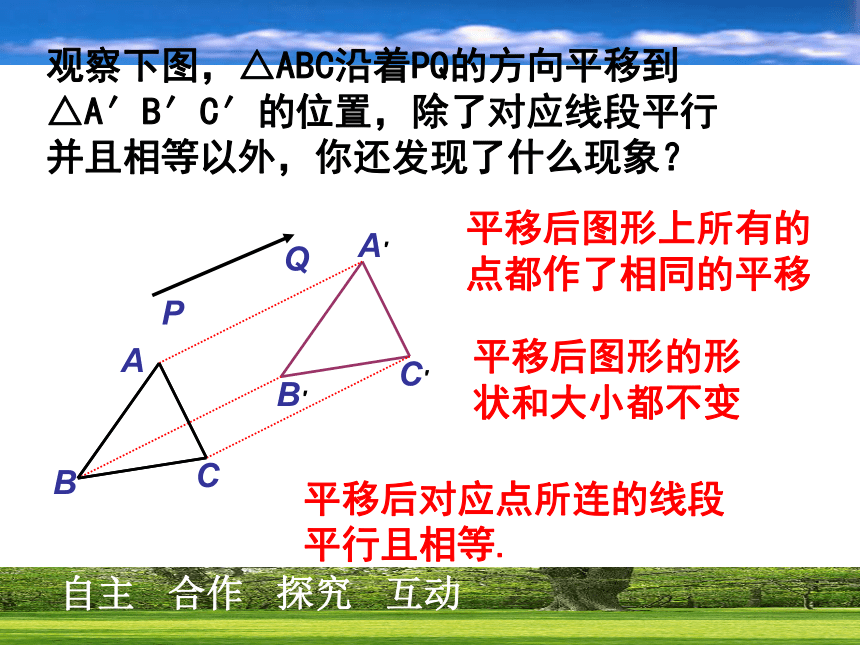
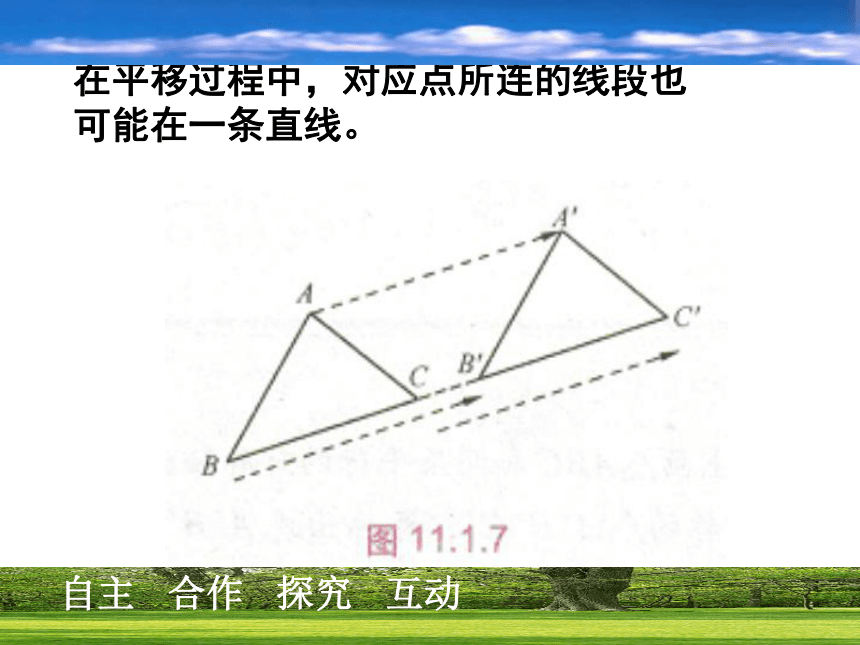
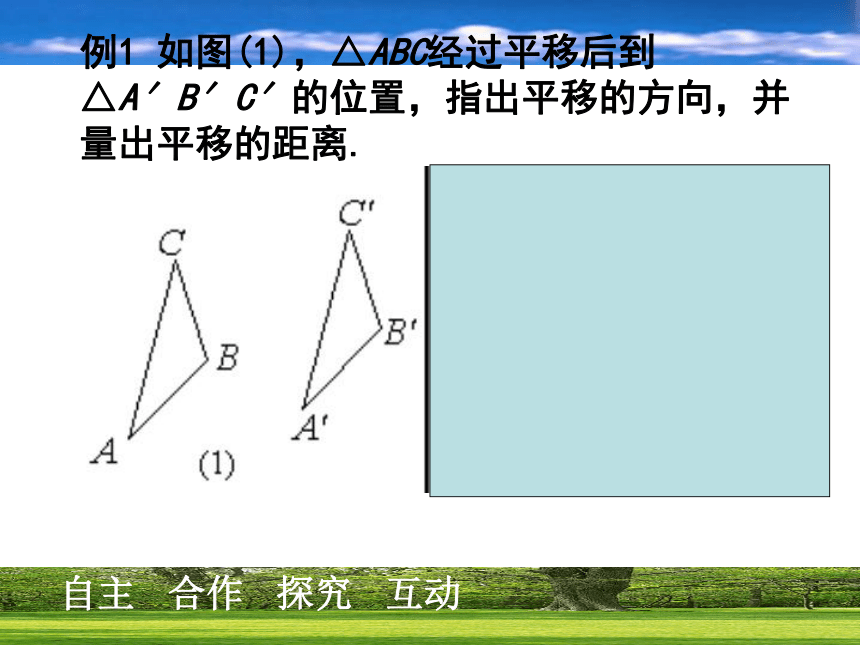
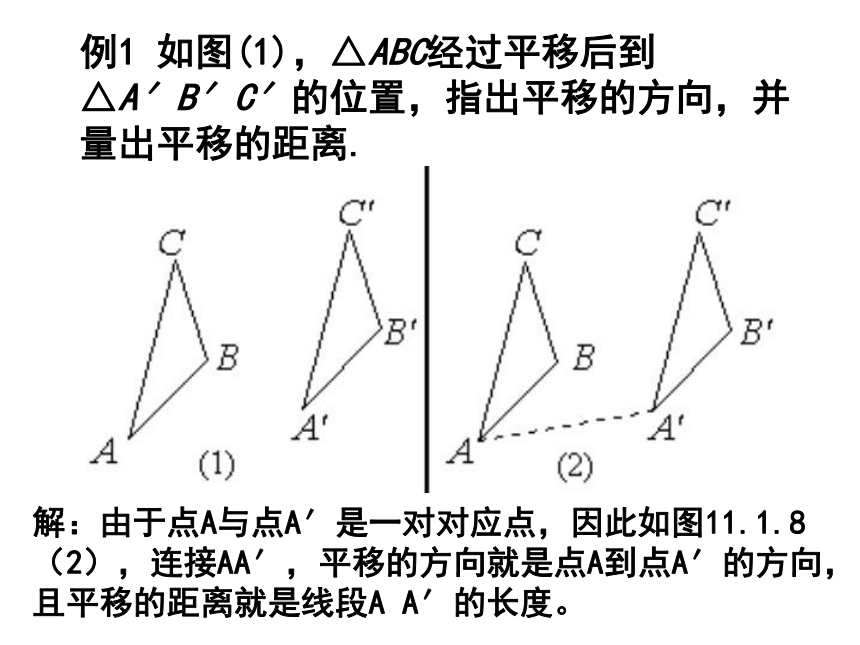
B′C′= ,∠A′=∠ . 请大家结合上题说说平移有什么特征? 对应线段平行(或在一条直线上)对应线段相等对应角相等.观察下图,△ABC沿着PQ的方向平移到△A′B′C′的位置,除了对应线段平行并且相等以外,你还发现了什么现象? BAPCA′QB′C′平移后对应点所连的线段平行且相等.平移后图形的形状和大小都不变 平移后图形上所有的点都作了相同的平移在平移过程中,对应点所连的线段也可能在一条直线。例1 如图(1),△ABC经过平移后到△A′B′C′的位置,指出平移的方向,并量出平移的距离. 例1 如图(1),△ABC经过平移后到△A′B′C′的位置,指出平移的方向,并量出平移的距离. 解:由于点A与点A′是一对对应点,因此如图11.1.8(2),连接AA′,平移的方向就是点A到点A′的方向,且平移的距离就是线段A A′的长度。试一试在如图的方格纸中,画出将图中的△ABC向右平移5格后的△A′B′C′,然后再画出将△A′B′C′向上平移2格后的△A′′B′′C′′. △A′′B′′C′′是否可以看成是△ABC经过一次平移而得到的呢?如果是,那么平移的方向和距离是什么呢? 试一试在如图的方格纸中,画出将图中的△ABC向右平移5格后的△A′B′C′,然后再画出将△A′B′C′向上平移2格后的△A′′B′′C′′. △A′′B′′C′′是否可以看成是△ABC经过一次平移而得到的呢?如果是,那么平移的方向和距离是什么呢? 解 如上图右.△A′′B′′C′′可以看成是△ABC经过一次平移而得到的,平移的方向是点A到点A′′的方向,平移的距离是线段AA′′的长度. 例2 按下列要求画出图形:
(1)画出点A沿着线段PQ的方向平移到点A′的位置,平移的距离是线段PQ的长度; PQA(2)画出线段AB沿着线段MN的方向平移到A′B′的位置,平移的距离是3cm;MNAB(3)画出△ABC沿着线段MN的方向平移后的位置,平移的距离是线段MN的长度;NMBAC要正确画出一个图形按要求平移后的新图形,只要先画出关键点的对应点,如线段的端点、三角形的顶点、圆的圆心等等,就很容易画出新图形了mABCn(4)如图,画出关于直线m对称的,再画出关于直线n对称的观察和,两个三角形有什么关系吗?挑战自我如图,梯形ABCD中,AD∥BC,且AB=CD,
(1)怎样将线段AB作平移,使得经变换所得的像把梯形ABCD分割成一个平行四边形和一个三角形?请叙述这个平移的过程,并画出图形;
(2)说出第(1)题中所得三角形的一个性质,并说明理由。小结1、平移的要素(1)平移的方向,(2)平移的距离。2、平移后对应点的连结线段互相平行且相等,或是在同一条直线上;对应线段平行且相等(或在同一直线上);对应角相等。3、平移后的图形形状和大小不变。4、“多次平移相当于一次平移”。祝同学们学习进步!
同时也有
A′C′∥ ,A′C′= ,∠C′=∠ .
B′C′= ,∠A′=∠ . 请大家结合上题说说平移有什么特征? 对应线段平行(或在一条直线上)对应线段相等对应角相等.观察下图,△ABC沿着PQ的方向平移到△A′B′C′的位置,除了对应线段平行并且相等以外,你还发现了什么现象? BAPCA′QB′C′平移后对应点所连的线段平行且相等.平移后图形的形状和大小都不变 平移后图形上所有的点都作了相同的平移在平移过程中,对应点所连的线段也可能在一条直线。例1 如图(1),△ABC经过平移后到△A′B′C′的位置,指出平移的方向,并量出平移的距离. 例1 如图(1),△ABC经过平移后到△A′B′C′的位置,指出平移的方向,并量出平移的距离. 解:由于点A与点A′是一对对应点,因此如图11.1.8(2),连接AA′,平移的方向就是点A到点A′的方向,且平移的距离就是线段A A′的长度。试一试在如图的方格纸中,画出将图中的△ABC向右平移5格后的△A′B′C′,然后再画出将△A′B′C′向上平移2格后的△A′′B′′C′′. △A′′B′′C′′是否可以看成是△ABC经过一次平移而得到的呢?如果是,那么平移的方向和距离是什么呢? 试一试在如图的方格纸中,画出将图中的△ABC向右平移5格后的△A′B′C′,然后再画出将△A′B′C′向上平移2格后的△A′′B′′C′′. △A′′B′′C′′是否可以看成是△ABC经过一次平移而得到的呢?如果是,那么平移的方向和距离是什么呢? 解 如上图右.△A′′B′′C′′可以看成是△ABC经过一次平移而得到的,平移的方向是点A到点A′′的方向,平移的距离是线段AA′′的长度. 例2 按下列要求画出图形:
(1)画出点A沿着线段PQ的方向平移到点A′的位置,平移的距离是线段PQ的长度; PQA(2)画出线段AB沿着线段MN的方向平移到A′B′的位置,平移的距离是3cm;MNAB(3)画出△ABC沿着线段MN的方向平移后的位置,平移的距离是线段MN的长度;NMBAC要正确画出一个图形按要求平移后的新图形,只要先画出关键点的对应点,如线段的端点、三角形的顶点、圆的圆心等等,就很容易画出新图形了mABCn(4)如图,画出关于直线m对称的,再画出关于直线n对称的观察和,两个三角形有什么关系吗?挑战自我如图,梯形ABCD中,AD∥BC,且AB=CD,
(1)怎样将线段AB作平移,使得经变换所得的像把梯形ABCD分割成一个平行四边形和一个三角形?请叙述这个平移的过程,并画出图形;
(2)说出第(1)题中所得三角形的一个性质,并说明理由。小结1、平移的要素(1)平移的方向,(2)平移的距离。2、平移后对应点的连结线段互相平行且相等,或是在同一条直线上;对应线段平行且相等(或在同一直线上);对应角相等。3、平移后的图形形状和大小不变。4、“多次平移相当于一次平移”。祝同学们学习进步!
