苏教版五年级上册数学多边形的面积课件(共24张PPT)
文档属性
| 名称 | 苏教版五年级上册数学多边形的面积课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-12 08:42:18 | ||
图片预览







文档简介
(共24张PPT)
面 积 那 些 事
苏教版五年级数学上册
多边形的面积这单元主要学习了哪些知识呢?
活动一
理一理
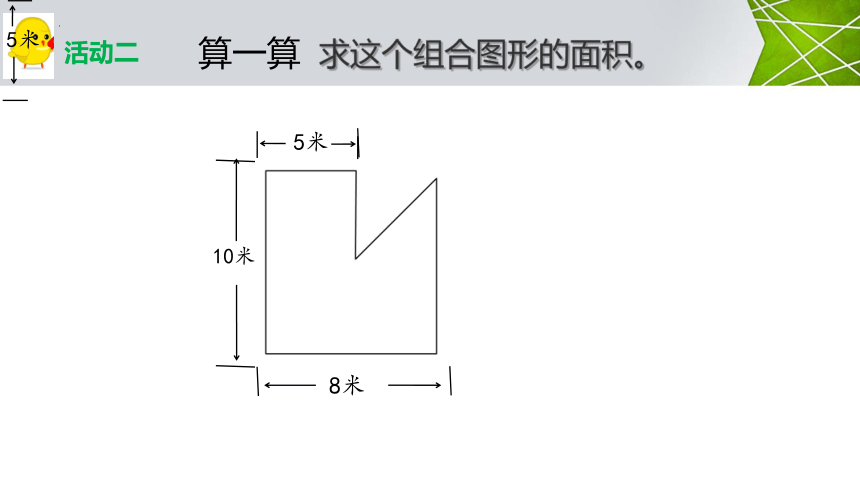
算一算 求这个组合图形的面积。
活动二
5米
10米
8米
5米
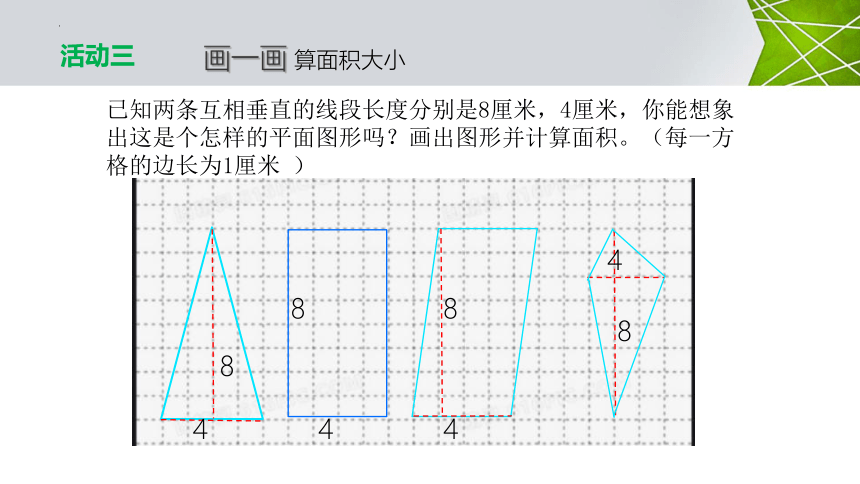
已知两条互相垂直的线段长度分别是8厘米,4厘米,你能想象出这是个怎样的平面图形吗?画出图形并计算面积。(每一方格的边长为1厘米 )
活动三
画一画 算面积大小
已知两条互相垂直的线段长度分别是8厘米,4厘米,你能想象出这是个怎样的平面图形吗?画出图形并计算面积。(每一方格的边长为1厘米 )
活动三
画一画 算面积大小
4
8
4
4
4
8
8
8
已知两条互相垂直的线段长度分别是8厘米,4厘米,你能想象出这是个怎样的平面图形吗?画出图形并计算面积。(每一方格的边长为1厘米 )
活动三
画一画 算面积大小
已知两条互相垂直的线段长度分别是8厘米,4厘米,你能想象出这是个怎样的平面图形吗?画出图形并计算面积。(每一方格的边长为1厘米 )
活动三
画一画 算面积大小
甲
乙
下课了!
再见!
总结梳理
正确应用公式
合理使用单位
灵活选择方法
简单图形(公式)
组合图形(割补法)
不规则图形(数方格等)
统一单位(进率)
理解推导过程(关系)
面积
那些事
通过今天的学习,你有哪些收获?
甲、乙两块绿地的面积,哪一块更大。
活动三
10m
10m
甲
乙
10m
活动四
说一说
总结梳理
正确应用公式
合理使用单位
灵活选择方法
简单图形(公式)
组合图形(割补法)
不规则图形(数方格等)
统一单位(进率)
理解推导过程(关系)
面积
那些事
转化
整体、联系
合理、简便
通过今天的学习,你有哪些收获?
典型例题
根据图形特点,选择合理、简便的方法
在利用割补法进行转化的过程中要注意什么?
组合图形
转化
(割补法)
基本图形
刨根问底
5
8
6
10
正确应用公式
内容梳理
合理使用单位
灵活选择方法
简单图形(公式)
组合图形(割补法)
不规则图形(数方格等)
统一单位(进率)
理解推导过程(联系)
面积
那点事
计算下面图形的面积。(单位:米)
典型例题
5×6=30(平方米)
30+15=45(平方米)
长方形面积:
梯形的面积:
总面积:
(5+10)×(8-6)÷2
=15×2÷2
=15(平方米)
分割
2.计算下面图形的面积。(单位:米)
典型例题
10×(8-6)÷2=10(平方米)
10+35=45(平方米)
三角形面积:
梯形的面积:
总面积:
(6+8)×5÷2
=14×5÷2
=35(平方米)
分割
典型例题
5×8=40(平方米)
40+5=45(平方米)
长方形面积:
三角形的面积:
总面积:
(10-5)×(8-6)÷2
=5×2÷2
=5(平方米)
计算下面图形的面积。(单位:米)
分割
2.计算下面图形的面积。(单位:米)
典型例题
10×8=80(平方米)
80-35=45(平方米)
长方形面积:
梯形面积:
总面积:
(6+8)×(10-5)÷2
=14×5÷2
=35(平方米)
添补
典型例题
分割
分割
分割
添补
分割成几个简单图形,分别算出面积,再求和。
添补成简单的图形,从补成的图形中去掉一部分。
组合图形
转化
(割补法)
基本图形
典型例题
根据图形特点,选择合理、简便的方法
在利用割补法进行转化的过程中要注意什么?
组合图形
转化
(割补法)
基本图形
刨根问底
典型例题
3.不规则图形面积计算。
估算
只算整格,得到的结果比实际面积小。
不满整格当作整格,得到的结果比实际面积大。
(实际面积的范围在这两种结果之间。)
先数整格的,再数不满整格的,把不满整格的
按半格计算,让估算的结果更加接近实际面积。
巩固练习
2.下图是由两个正方形组成,求阴影部分的面积。(单位:米)
总:8×8+4×4=80(平方米)
三角形:(8+4)×8÷2=48(平方米)
阴影:80-48=32 (平方米)
8
4
活动四
下图中,大平行四边形的底是20厘米,高是5厘米,虚线将大平行四边形分成两个小平行四边形,涂色部分的面积是多少厘米?请说明理由。
面 积 那 些 事
苏教版五年级数学上册
多边形的面积这单元主要学习了哪些知识呢?
活动一
理一理
算一算 求这个组合图形的面积。
活动二
5米
10米
8米
5米
已知两条互相垂直的线段长度分别是8厘米,4厘米,你能想象出这是个怎样的平面图形吗?画出图形并计算面积。(每一方格的边长为1厘米 )
活动三
画一画 算面积大小
已知两条互相垂直的线段长度分别是8厘米,4厘米,你能想象出这是个怎样的平面图形吗?画出图形并计算面积。(每一方格的边长为1厘米 )
活动三
画一画 算面积大小
4
8
4
4
4
8
8
8
已知两条互相垂直的线段长度分别是8厘米,4厘米,你能想象出这是个怎样的平面图形吗?画出图形并计算面积。(每一方格的边长为1厘米 )
活动三
画一画 算面积大小
已知两条互相垂直的线段长度分别是8厘米,4厘米,你能想象出这是个怎样的平面图形吗?画出图形并计算面积。(每一方格的边长为1厘米 )
活动三
画一画 算面积大小
甲
乙
下课了!
再见!
总结梳理
正确应用公式
合理使用单位
灵活选择方法
简单图形(公式)
组合图形(割补法)
不规则图形(数方格等)
统一单位(进率)
理解推导过程(关系)
面积
那些事
通过今天的学习,你有哪些收获?
甲、乙两块绿地的面积,哪一块更大。
活动三
10m
10m
甲
乙
10m
活动四
说一说
总结梳理
正确应用公式
合理使用单位
灵活选择方法
简单图形(公式)
组合图形(割补法)
不规则图形(数方格等)
统一单位(进率)
理解推导过程(关系)
面积
那些事
转化
整体、联系
合理、简便
通过今天的学习,你有哪些收获?
典型例题
根据图形特点,选择合理、简便的方法
在利用割补法进行转化的过程中要注意什么?
组合图形
转化
(割补法)
基本图形
刨根问底
5
8
6
10
正确应用公式
内容梳理
合理使用单位
灵活选择方法
简单图形(公式)
组合图形(割补法)
不规则图形(数方格等)
统一单位(进率)
理解推导过程(联系)
面积
那点事
计算下面图形的面积。(单位:米)
典型例题
5×6=30(平方米)
30+15=45(平方米)
长方形面积:
梯形的面积:
总面积:
(5+10)×(8-6)÷2
=15×2÷2
=15(平方米)
分割
2.计算下面图形的面积。(单位:米)
典型例题
10×(8-6)÷2=10(平方米)
10+35=45(平方米)
三角形面积:
梯形的面积:
总面积:
(6+8)×5÷2
=14×5÷2
=35(平方米)
分割
典型例题
5×8=40(平方米)
40+5=45(平方米)
长方形面积:
三角形的面积:
总面积:
(10-5)×(8-6)÷2
=5×2÷2
=5(平方米)
计算下面图形的面积。(单位:米)
分割
2.计算下面图形的面积。(单位:米)
典型例题
10×8=80(平方米)
80-35=45(平方米)
长方形面积:
梯形面积:
总面积:
(6+8)×(10-5)÷2
=14×5÷2
=35(平方米)
添补
典型例题
分割
分割
分割
添补
分割成几个简单图形,分别算出面积,再求和。
添补成简单的图形,从补成的图形中去掉一部分。
组合图形
转化
(割补法)
基本图形
典型例题
根据图形特点,选择合理、简便的方法
在利用割补法进行转化的过程中要注意什么?
组合图形
转化
(割补法)
基本图形
刨根问底
典型例题
3.不规则图形面积计算。
估算
只算整格,得到的结果比实际面积小。
不满整格当作整格,得到的结果比实际面积大。
(实际面积的范围在这两种结果之间。)
先数整格的,再数不满整格的,把不满整格的
按半格计算,让估算的结果更加接近实际面积。
巩固练习
2.下图是由两个正方形组成,求阴影部分的面积。(单位:米)
总:8×8+4×4=80(平方米)
三角形:(8+4)×8÷2=48(平方米)
阴影:80-48=32 (平方米)
8
4
活动四
下图中,大平行四边形的底是20厘米,高是5厘米,虚线将大平行四边形分成两个小平行四边形,涂色部分的面积是多少厘米?请说明理由。
