第12章 全等三角形 单元同步检测试题(含答案)
文档属性
| 名称 | 第12章 全等三角形 单元同步检测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 264.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-13 13:33:25 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十二章《全等三角形》单元检测题
一、选择题(每题3分,共30分)
1.如图所示的图形全等的是( )
A. B. C. D.
2.如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A.12 B.7 C.2 D.14
3.如图,△AOC≌△BOD,点A与点B是对应点,那么下列结论中错误的是( )
A.AB=CD B.AC=BD C.AO=BO D.∠A=∠B
4.下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等,其中真命题的个数有 ( )
A.3个 B.2个 C.1个 D.0个
5.如图12 -4-3,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌△POD的是 ( )
A.PC⊥ OA ,PD⊥ OB B.OC= OD C.∠OPC = ∠OPD D.PC = PD
6.如图12-4-4,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是 ( )
A.AC=BD B.∠CAB= ∠DBA C.∠C= ∠D D.BC=AD
7.如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=12,AC=8,则CD的长为( )
A. 5.5 B.4 C.4.5 D.3
8.如图,AD是△ABC的角平分线,DF⊥AB于点F,且DE=DG,S△ADG=24,S△AED=18,则△DEF的面积为( )
A.2 B.3 C.4 D.6
9.如图,△ABC≌△A′B′C′,边B′C′过点A且平分∠BAC交BC于点D,∠B=26°,∠CDB′=94°,则∠C′的度数为( )
A.34° B.40° C.45° D.60°
10.如图,在△ABC中,BD、AE分别是△ABC的角平分线和高线,过点D作DF⊥AB于点F,若AB=4,BC=6,DF=2,则AE的长为( )
A.3 B. C. D.
二、填空题(每题3分,共24分)
11.如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是 .
12.如图,已知AB=DB,只添加一个条件就能判定△ABC≌△DBC,则你添加的条件是 .(写出一个即可)
13.如图,AB⊥AC,DC⊥DB,AC,BD相交于点O,若AB=CD,利用 可判定△ABC≌△DCB.
14.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,若利用“HL”证明Rt△ABC≌Rt△DCB,你添加的条件是 .(不添加字母和辅助线)
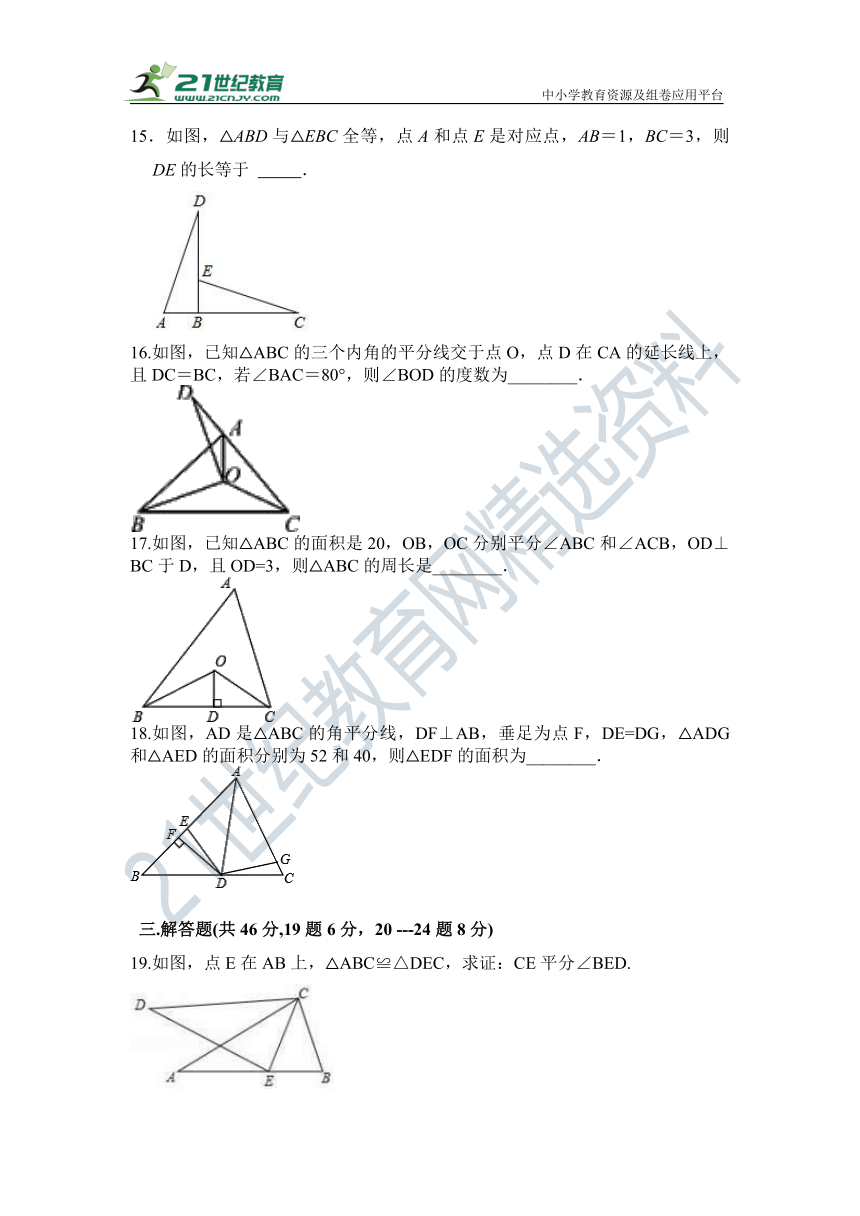
15.如图,△ABD与△EBC全等,点A和点E是对应点,AB=1,BC=3,则DE的长等于 .
16.如图,已知△ABC的三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,若∠BAC=80°,则∠BOD的度数为________.
17.如图,已知△ABC的面积是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是________.
18.如图,AD是△ABC的角平分线,DF⊥AB,垂足为点F,DE=DG,△ADG和△AED的面积分别为52和40,则△EDF的面积为________.
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.
20.如图,点O是线段AB的中点,OD∥BC且OD=BC.
(1)求证:△AOD≌△OBC;
(2)若∠ADO=35°,求∠DOC的度数.
21.如图,AD⊥AE,AB⊥AC,AD=AE,AB=AC.求证:△ABD≌△ACE.
22.如图,AC∥BE,点D在BC上,AB=DE,∠ABE=∠CDE.
求证:DC=BE-AC.
23.如图,四边形ABCD中,AB∥CD,CD=AD,∠ADC=60°,对角线BD平分∠ABC交AC于点P.CE是∠ACB的角平分线,交BD于点O.
(1)请求出∠BAC的度数;
(2)试用等式表示线段BE、BC、CP之间的数量关系,并说明理由.
24.为了解学生对所学知识的应用能力,某校老师在七年级数学兴趣小组活动中,设置了这样的问题:因为池塘两端A,B的距离无法直接测量,请同学们设计方案测量A,B的距离.甲、乙两位同学分别设计出了如下两种方案:
甲:如图①,先在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使CO=AO,DO=BO,连接DC,测出DC的长即可.
乙:如图②,先确定直线AB,过点B作直线BE,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即可.
(1)甲、乙两同学的方案哪个可行?
(2)请说明方案可行的理由.
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A C C B D B A C
二、填空题
11.解:∵四边形ABCD≌四边形A'B'C'D',
∴∠D=∠D′=130°,
∴∠A=360°﹣∠B﹣∠C﹣∠D=360°﹣75°﹣60°﹣130°=95°,
故答案为:95°.
12.解:∵AB=DB,
而BC=BC,
∴当AC=CD时,可根据“SSS”判断△ABC≌△DBC;
当∠ABC=∠DBC时,可根据“SAS”判断△ABC≌△DBC.
故答案为AC=DC或∠ABC=∠DBC.
13.解:∵AB⊥AC,DC⊥DB,
∴∠BAC=∠CDB=90°,
在Rt△ABC和Rt△DCB中,
,
∴Rt△ABC≌Rt△DCB(HL),
故答案为:HL.
14.解:∵斜边与直角边对应相等的两个直角三角形全等,
∴在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,使Rt△ABC≌Rt△DCB,添加的条件是:AB=DC.
故答案为:AB=DC(答案不唯一)
15.解:∵△ABD≌△EBC,AB=1,BC=3,
∴BE=AB=1,BD=BC=3,
∴DE=BD﹣BE=3﹣1=2,
故答案为:2.
16.【答案】 100°
17.【答案】
18.【答案】 6
三、解答题
19.证明:∵△ABC≌△DEC,
∴∠B=∠DEC,BC=EC,
∴∠B=∠BEC,
∴∠BEC=∠DEC,
∴CE平分∠BED.
20. (1)证明:
∵点O是线段AB的中点,∴AO=BO,
∵OD∥BC,∴∠AOD=∠OBC,
在△AOD与△OBC中,
,
∴△AOD≌△OBC(SAS);
(2)解:∵△AOD≌△OBC,∴∠ADO=∠OCB=35°,
∵OD∥BC,
∴∠DOC=∠OCB=35°.
21.证明:∵AD⊥AE,AB⊥AC,∴∠CAB=∠DAE=90°.
∴∠CAB+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE.
22.证明:∵AC∥BE,∴∠DBE=∠C.∵∠CDE=∠DBE+∠E,∠ABE=∠ABC+∠DBE,∠ABE=∠CDE,∴∠E=∠ABC.在△ABC与△DEB中,∴△ABC≌△DEB(AAS).∴BC=BE,AC=BD.∴DC=BC-BD=BE-AC.
23.【解答】(1)解:∵CD=AD,∠ADC=60°,
∴△ACD为等边三角形,
∴∠ACD=60°,
∵AB∥CD,
∴∠BAC=∠ACD=60°;
(2)证明:在BC上截取BF=BE,
∵BD平分∠ABC,
∴∠EBO=∠OBF,
∵OB=OB,
∴△BEO≌△BFO(SAS),
∴∠BOE=∠BOF,
∵∠BAC=60°,CE是∠ACB的角平分线,
∴∠OBC+∠OCB=60°,
∴∠POC=∠BOE=60°,
∴∠COF=60°,
∴∠COF=∠POC,
又∵OC=OC,∠OCP=∠OCF,
∴△CPO≌△CFO(ASA),
∴CP=CF,
∴BC=BF+CF=BE+CP.
24.【解答】解:(1)甲同学的方案可行;
(2)甲同学方案:
在△ABO和△CDO中,
,
∴△ABO≌△CDO(SAS),
∴AB=CD;
乙同学方案:
在△ABD和△CBD中,
只能知道DC=DA,DB=DB,不能判定△ABD与△CBD全等,故方案不可行.
www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第十二章《全等三角形》单元检测题
一、选择题(每题3分,共30分)
1.如图所示的图形全等的是( )
A. B. C. D.
2.如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A.12 B.7 C.2 D.14
3.如图,△AOC≌△BOD,点A与点B是对应点,那么下列结论中错误的是( )
A.AB=CD B.AC=BD C.AO=BO D.∠A=∠B
4.下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等,其中真命题的个数有 ( )
A.3个 B.2个 C.1个 D.0个
5.如图12 -4-3,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌△POD的是 ( )
A.PC⊥ OA ,PD⊥ OB B.OC= OD C.∠OPC = ∠OPD D.PC = PD
6.如图12-4-4,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是 ( )
A.AC=BD B.∠CAB= ∠DBA C.∠C= ∠D D.BC=AD
7.如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=12,AC=8,则CD的长为( )
A. 5.5 B.4 C.4.5 D.3
8.如图,AD是△ABC的角平分线,DF⊥AB于点F,且DE=DG,S△ADG=24,S△AED=18,则△DEF的面积为( )
A.2 B.3 C.4 D.6
9.如图,△ABC≌△A′B′C′,边B′C′过点A且平分∠BAC交BC于点D,∠B=26°,∠CDB′=94°,则∠C′的度数为( )
A.34° B.40° C.45° D.60°
10.如图,在△ABC中,BD、AE分别是△ABC的角平分线和高线,过点D作DF⊥AB于点F,若AB=4,BC=6,DF=2,则AE的长为( )
A.3 B. C. D.
二、填空题(每题3分,共24分)
11.如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是 .
12.如图,已知AB=DB,只添加一个条件就能判定△ABC≌△DBC,则你添加的条件是 .(写出一个即可)
13.如图,AB⊥AC,DC⊥DB,AC,BD相交于点O,若AB=CD,利用 可判定△ABC≌△DCB.
14.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,若利用“HL”证明Rt△ABC≌Rt△DCB,你添加的条件是 .(不添加字母和辅助线)
15.如图,△ABD与△EBC全等,点A和点E是对应点,AB=1,BC=3,则DE的长等于 .
16.如图,已知△ABC的三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,若∠BAC=80°,则∠BOD的度数为________.
17.如图,已知△ABC的面积是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是________.
18.如图,AD是△ABC的角平分线,DF⊥AB,垂足为点F,DE=DG,△ADG和△AED的面积分别为52和40,则△EDF的面积为________.
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.
20.如图,点O是线段AB的中点,OD∥BC且OD=BC.
(1)求证:△AOD≌△OBC;
(2)若∠ADO=35°,求∠DOC的度数.
21.如图,AD⊥AE,AB⊥AC,AD=AE,AB=AC.求证:△ABD≌△ACE.
22.如图,AC∥BE,点D在BC上,AB=DE,∠ABE=∠CDE.
求证:DC=BE-AC.
23.如图,四边形ABCD中,AB∥CD,CD=AD,∠ADC=60°,对角线BD平分∠ABC交AC于点P.CE是∠ACB的角平分线,交BD于点O.
(1)请求出∠BAC的度数;
(2)试用等式表示线段BE、BC、CP之间的数量关系,并说明理由.
24.为了解学生对所学知识的应用能力,某校老师在七年级数学兴趣小组活动中,设置了这样的问题:因为池塘两端A,B的距离无法直接测量,请同学们设计方案测量A,B的距离.甲、乙两位同学分别设计出了如下两种方案:
甲:如图①,先在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使CO=AO,DO=BO,连接DC,测出DC的长即可.
乙:如图②,先确定直线AB,过点B作直线BE,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即可.
(1)甲、乙两同学的方案哪个可行?
(2)请说明方案可行的理由.
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A C C B D B A C
二、填空题
11.解:∵四边形ABCD≌四边形A'B'C'D',
∴∠D=∠D′=130°,
∴∠A=360°﹣∠B﹣∠C﹣∠D=360°﹣75°﹣60°﹣130°=95°,
故答案为:95°.
12.解:∵AB=DB,
而BC=BC,
∴当AC=CD时,可根据“SSS”判断△ABC≌△DBC;
当∠ABC=∠DBC时,可根据“SAS”判断△ABC≌△DBC.
故答案为AC=DC或∠ABC=∠DBC.
13.解:∵AB⊥AC,DC⊥DB,
∴∠BAC=∠CDB=90°,
在Rt△ABC和Rt△DCB中,
,
∴Rt△ABC≌Rt△DCB(HL),
故答案为:HL.
14.解:∵斜边与直角边对应相等的两个直角三角形全等,
∴在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,使Rt△ABC≌Rt△DCB,添加的条件是:AB=DC.
故答案为:AB=DC(答案不唯一)
15.解:∵△ABD≌△EBC,AB=1,BC=3,
∴BE=AB=1,BD=BC=3,
∴DE=BD﹣BE=3﹣1=2,
故答案为:2.
16.【答案】 100°
17.【答案】
18.【答案】 6
三、解答题
19.证明:∵△ABC≌△DEC,
∴∠B=∠DEC,BC=EC,
∴∠B=∠BEC,
∴∠BEC=∠DEC,
∴CE平分∠BED.
20. (1)证明:
∵点O是线段AB的中点,∴AO=BO,
∵OD∥BC,∴∠AOD=∠OBC,
在△AOD与△OBC中,
,
∴△AOD≌△OBC(SAS);
(2)解:∵△AOD≌△OBC,∴∠ADO=∠OCB=35°,
∵OD∥BC,
∴∠DOC=∠OCB=35°.
21.证明:∵AD⊥AE,AB⊥AC,∴∠CAB=∠DAE=90°.
∴∠CAB+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE.
22.证明:∵AC∥BE,∴∠DBE=∠C.∵∠CDE=∠DBE+∠E,∠ABE=∠ABC+∠DBE,∠ABE=∠CDE,∴∠E=∠ABC.在△ABC与△DEB中,∴△ABC≌△DEB(AAS).∴BC=BE,AC=BD.∴DC=BC-BD=BE-AC.
23.【解答】(1)解:∵CD=AD,∠ADC=60°,
∴△ACD为等边三角形,
∴∠ACD=60°,
∵AB∥CD,
∴∠BAC=∠ACD=60°;
(2)证明:在BC上截取BF=BE,
∵BD平分∠ABC,
∴∠EBO=∠OBF,
∵OB=OB,
∴△BEO≌△BFO(SAS),
∴∠BOE=∠BOF,
∵∠BAC=60°,CE是∠ACB的角平分线,
∴∠OBC+∠OCB=60°,
∴∠POC=∠BOE=60°,
∴∠COF=60°,
∴∠COF=∠POC,
又∵OC=OC,∠OCP=∠OCF,
∴△CPO≌△CFO(ASA),
∴CP=CF,
∴BC=BF+CF=BE+CP.
24.【解答】解:(1)甲同学的方案可行;
(2)甲同学方案:
在△ABO和△CDO中,
,
∴△ABO≌△CDO(SAS),
∴AB=CD;
乙同学方案:
在△ABD和△CBD中,
只能知道DC=DA,DB=DB,不能判定△ABD与△CBD全等,故方案不可行.
www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
