人教版2024-2025学年九年级上册数学同步讲义专题22.6二次函数的图象与系数的关系专项训练(30题)(学生版+解析)
文档属性
| 名称 | 人教版2024-2025学年九年级上册数学同步讲义专题22.6二次函数的图象与系数的关系专项训练(30题)(学生版+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 776.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-12 11:16:58 | ||
图片预览




文档简介
专题22.6 二次函数的图象与系数的关系专项训练(30题)
【人教版】
考卷信息:
本套训练卷共30题,题型针对性较高,覆盖面广,选题有深度,可加强学生对二次函数图象与各项系数符号之间的关系的理解!
【题型1 二次函数图象与系数的关系的单结论问题】
1.(23-24·四川成都·模拟预测)如图,二次函数的图象与轴交于,两点,下列说法正确的是( )
A.
B.抛物线的对称轴是直线
C.当时,的值随值的增大而减小
D.
2.(23-24九年级·河南商丘·阶段练习)如图为抛物线的图象,A、B、C 为抛物线与坐标轴的交点,且,则下列关系中正确的是( )
A. B. C. D.
3.(23-24·湖北鄂州·模拟预测)如图,二次函数()的图象关于直线对称,则下列结论正确的是( )
A.
B.若抛物线与x轴交于,两点,则
C.
D.对任意实数t,总有
4.(23-24·广西钦州·三模)在平面直角坐标系中,二次函数的图像如图所示,以下结论中正确的是( )
A.
B.
C.
D.若为任意实数,则
5.(23-24·浙江温州·二模)已知二次函数的图象如图所示,则下列选项中错误的是( ).
A. B.的解为,
C. D.点在第三象限
6.(23-24九年级·湖北黄冈·期中)已知二次函数的图象如图所示,对称轴为直线,且经过点,下列结论中正确的是( )
A. B.
C. D.当时,y随x的增大而增大
7.(23-24·山东青岛·一模)如图,已知抛物线()的顶点坐标是,与x轴的两个交点是A,B,其中点B的坐标是,则下列结论正确的是:( )
A. B.
C.点A的坐标为 D.
8.(23-24九年级·湖北黄冈·期中)在平面直角坐标系xOy中,O为坐标原点,抛物线 的对称轴为 与x轴的一个交点位于,两点之间.下列结论:其中正确的是( )
A. B.
C. D.若、为方程 的两个根,则
9.(23-24·浙江·一模)抛物线的顶点为,且经过点,其部分图象如图所示,则下列结论正确的是( )
A.若抛物线经过点,则必过点
B.若点和都在抛物线上,则
C.
D.
10.(23-24九年级·四川绵阳·阶段练习)已知抛物线,且,.则下列结论中错误的是( )
A.点和在抛物线上 B.抛物线与x轴负半轴必有一个交点
C. D.当时,y有最小值为8a
11.(23-24九年级·全国·竞赛)已知开口向上的抛物线经过点,且,则的取值范围是( ).
A. B.
C. D.
12.(23-24九年级·河南郑州·期末)如图,二次函数的图象与轴分别交于A、B两点,与轴交于点,点的坐标为,下列结论中正确的是( )
A. B. C. D.
【题型2 二次函数图象与系数的关系的多结论问题】
13.(23-24·四川成都·模拟预测)如图,抛物线与x轴交于点,,
与y轴交于点C.有下列说法:①;②抛物线的对称轴为直线;③当时,;④当时,y的值随x值的增大而减小;⑤(m为任意实数).其中正确的有( )
A.1个 B.2个 C.3个 D.4个
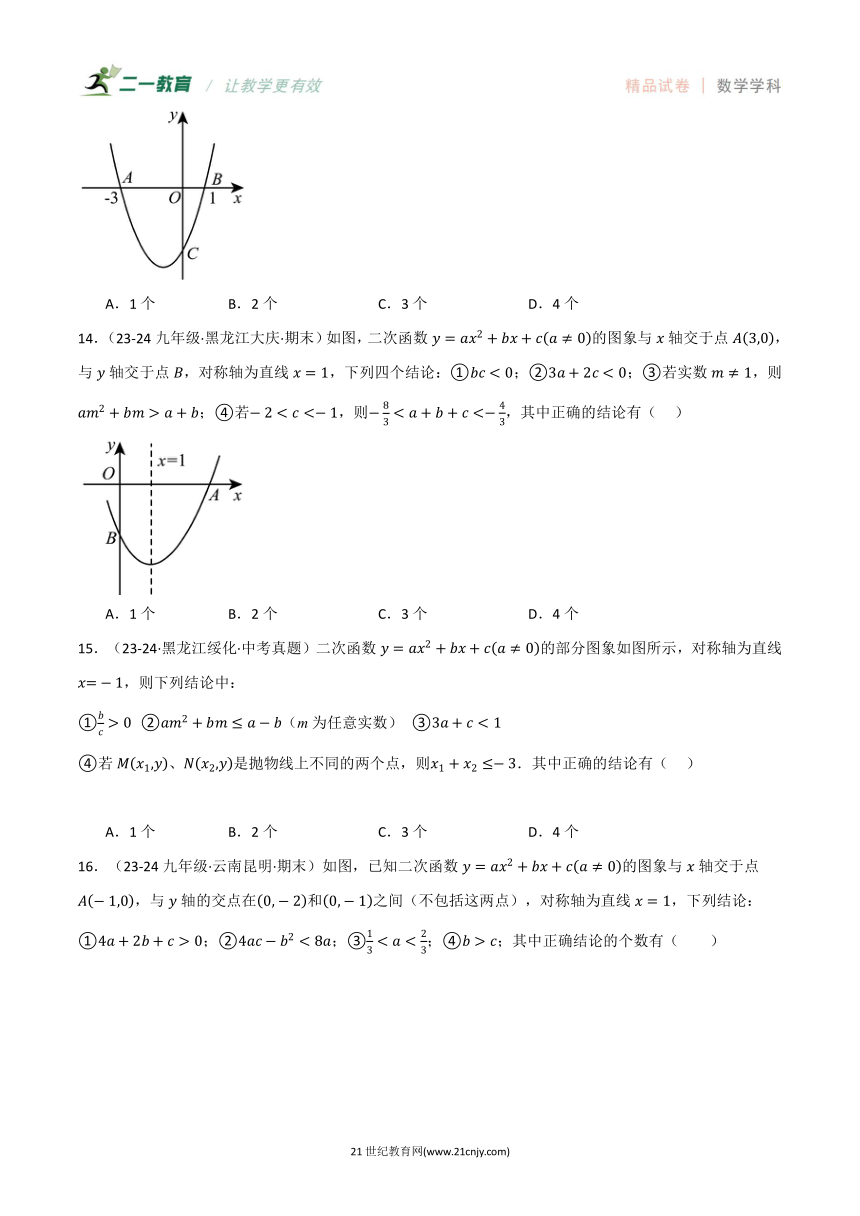
14.(23-24九年级·黑龙江大庆·期末)如图,二次函数的图象与轴交于点,与轴交于点,对称轴为直线,下列四个结论:①;②;③若实数,则;④若,则,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
15.(23-24·黑龙江绥化·中考真题)二次函数的部分图象如图所示,对称轴为直线,则下列结论中:
① ②(m为任意实数) ③
④若、是抛物线上不同的两个点,则.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
16.(23-24九年级·云南昆明·期末)如图,已知二次函数的图象与轴交于点,与轴的交点在和之间(不包括这两点),对称轴为直线,下列结论:①;②;③;④;其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
17.(23-24九年级·湖北宜昌·阶段练习)如图,己知开口向下的抛物线与x轴交于点,对称轴为直线.则下列结论:①;②;③;④抛物线上有两点和,若且,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
18.(23-24九年级·云南·期末)二次函数的部分图象如图,图象过点下列结论:①;②;③;④;⑤若顶点坐标为,则方程没有实数根.其中正确的结论有( )
A.个 B.个 C.个 D.个
19.(23-24·新疆乌鲁木齐·一模)如图,二次函数的图象与x轴负半轴交于,顶点坐标为,有以下结论:①;②;③若点,,,均在函数图象上,则;④对于任意m都有;⑤点M,N是抛物线与x轴的两个交点,若在x轴下方的抛物线上存在一点P,使得,则a的范围为.其中结论正确的有( )
A.5个 B.4个 C.3个 D.2个
20.(23-24九年级·山东烟台·期中)已知二次函数,图象的一部分如图所示,该函数图象经过点,顶点坐标为.对于下列结论:①;②;③若关于x的一元二次方程无实数根,则;④)(其中)﹔⑤若和均在该函数图象上,且,则.其中正确结论有( )
A.②③④ B.②③⑤ C.②③ D.④⑤
21.(23-24·山东滨州·一模)如图,抛物线经过点,顶点为,且抛物线与y轴的交点B在和之间(不含端点),小明同学得出了下列结论:①当时,;②a的取范围为;③当时,的面积为.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
22.(23-24九年级·湖北武汉·期末)已知二次函数(,为常数且)经过,且,下列结论: ; ;若关于的方程有整数解,则符合条件的的值有个;当时,二次函数的最大值为,则.
其中一定正确的有 .(填序号即可)
23.(23-24九年级·湖北·阶段练习)已知抛物线 (a,b,c均为常数)的顶点坐标为 其中,与x轴的一个交点位于和之间,则下列结论:
① ;
②;
③若该抛物线经过点,,则
④若关于x的一元二次方程 无实数根,则.
其中正确的结论是 .(只填序号)
24.(23-24九年级·福建福州·阶段练习)如图所示,二次函数的图像的对称轴是直线,且经过点.有下列结论:①;②;③(为常数);④和时函数值相等;⑤若,,在该函数图像上,则;⑥.其中错误的结论是 (填序号).
25.(23-24九年级·广西贵港·期末)如图,抛物线与轴正半轴交于两点,轴负半轴交于点.若点,则下列结论中: ; ; 与是抛物线上两点,若,则;若抛物线的对称轴是直线,为任意实数,则;若则其中正确结论的个数共有 个.
26.(23-24九年级·湖北武汉·阶段练习)如图,抛物线与x轴交于点,,交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①;②(m为任意实数);③若点P为对称轴上的动点,则有最大值,最大值为;④若m是方程的一个根,则一定有成立.其中正确的序号有 .
27.(23-24九年级·江西上饶·期末)如图,已知抛物线与x轴交于A、B两点,与y轴交于点C,顶点为D,其中点B坐标为(3,0),顶点D的横坐标为1,轴,垂足为E,下列结论:①当时,y随x增大而减小;②;③;④;⑤当时,.其中结论正确的有 .(填序号)(多填错填倒扣一分)
28.(23-24九年级·重庆·期末)如图,函数的图象过点和,下列判断:
①;
②;
③;
④和处的函数值相等.
其中正确的是 (只填序号).
29.(23-24九年级·广东广州·期末)抛物线y=ax2+bx+c中,b=4a,它的图象如图,有以下结论:①c>0;②a+b+c>0;③a﹣b+c>0 ④b2﹣4ac<0;⑤abc<0;⑥4a>c;其中正确的为 (填序号).
30.(23-24九年级·湖北武汉·阶段练习)已知二次函数的图象过点,,,且交轴的正半轴于点,下列结论: ; ;若直线与抛物线只有一个公共点,则;抛物线上的两点,,在的左边,若,则; ,请将所有正确的序号填在横线上 .21世纪教育网(www.21cnjy.com)
专题22.6 二次函数的图象与系数的关系专项训练(30题)
【人教版】
考卷信息:
本套训练卷共30题,题型针对性较高,覆盖面广,选题有深度,可加强学生对二次函数图象与各项系数符号之间的关系的理解!
【题型1 二次函数图象与系数的关系的单结论问题】
1.(23-24·四川成都·模拟预测)如图,二次函数的图象与轴交于,两点,下列说法正确的是( )
A.
B.抛物线的对称轴是直线
C.当时,的值随值的增大而减小
D.
【答案】C
【分析】本题主要考查了二次函数的图象与性质,根据图象与y轴交点即可判定,再利用二次函数的对称性和与轴交点求出对称轴,根据图象即可判断当时,图象位于对称轴右侧,随的增大而减小,再由当时,可得.
【详解】解:由图象可知:抛物线与y轴交于正半轴,
∴,A选项的结论不正确,不符合题意;
二次函数的图象与轴交于,两点,
∴对称轴为,故B选项的结论不正确,不符合题意;
由图象知:当时,图象位于对称轴右侧,随的增大而减小,故C选项的结论正确,符合题意;
当时,,故D选项的结论不正确,不符合题意.
故选:C.
2.(23-24九年级·河南商丘·阶段练习)如图为抛物线的图象,A、B、C 为抛物线与坐标轴的交点,且,则下列关系中正确的是( )
A. B. C. D.
【答案】D
【分析】根据以下知识点分析即可:①二次项系数决定抛物线的开口方向和大小:当时,抛物线向上开口;当时,抛物线向下开口;②一次项系数和二次项系数共同决定对称轴的位置:当与同号时(即,对称轴在轴左;当与异号时(即,对称轴在轴右.(简称:左同右异)③常数项决定抛物线与轴交点.抛物线与轴交于.此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确二次函数各项的系数和图形的关系.
【详解】解:,
,
又时,,
,
,
选项C不正确;
抛物线开口向上,
;
又,
,
选项A不正确;
,
,
又,
,
选项D正确;
,
时,,
,
又,
,
选项B不正确.
故选:D.
3.(23-24·湖北鄂州·模拟预测)如图,二次函数()的图象关于直线对称,则下列结论正确的是( )
A.
B.若抛物线与x轴交于,两点,则
C.
D.对任意实数t,总有
【答案】B
【分析】本题考查二次函数图象与系数的关系及抛物线与轴的交点,能根据所给函数图象得出,,的正负,再利用抛物线的对称性来求解,根据所给函数图象中抛物线的对称轴可得出,之间的等量关系,再结合抛物线与轴的交点情况可解决问题.
【详解】解:由图知开口向下,
,
与交于正半轴,
,
图象关于直线对称,
,
,
,A选项错误;
若抛物线与x轴交于,两点,
,则,故B选项正确;
,
,
由图知,当时,,
不成立,故C选项错误;
当时,有,故D选项错误.
故选:B.
4.(23-24·广西钦州·三模)在平面直角坐标系中,二次函数的图像如图所示,以下结论中正确的是( )
A.
B.
C.
D.若为任意实数,则
【答案】B
【分析】本题考查了二次函数的性质,根据二次函数的图象判断的符号,根据抛物线与轴的交点即可判断B,C选项,根据抛物线开口向上,对称轴为直线,得出最小值为,进而即可求解.
【详解】解:抛物线开口向上,则,
抛物线的对称轴为直线,则
∴,
抛物线与轴交于负半轴,则
∴,故A选项错误;
∵当时,,
∴
∴,故B正确
∵抛物线的对称轴为直线,和时,
∴,故C错误;
∵,对称轴为直线
∴若为任意实数,则,即,故D错误,
故选:B.
5.(23-24·浙江温州·二模)已知二次函数的图象如图所示,则下列选项中错误的是( ).
A. B.的解为,
C. D.点在第三象限
【答案】D
【分析】本题主要考查了二次函数图象的性质、不等式的性质等知识点,熟练掌握二次函数图象的性质成为解题的关键.
根据二次函数图象的性质逐项分析判断即可.
【详解】解:A、由图象可得:对称轴,即,即A选项正确,不符合题意;
B、由函数图象可知:的解为,另一个解为:,即B选项正确,不符合题意;
C、由函数图象可知:且,则有;又当时,,即,即,即C选项正确,不符合题意;
D、由意义可知:,则,又,则,可得点在第二象限,故D选项错误,符合题意.
故选D.
6.(23-24九年级·湖北黄冈·期中)已知二次函数的图象如图所示,对称轴为直线,且经过点,下列结论中正确的是( )
A. B.
C. D.当时,y随x的增大而增大
【答案】B
【分析】本题考查二次函数的图象与性质,能从图象中获取信息是解答的关键.根据图象的开口方向、与坐标轴的交点、对称轴位置、函数的增减性、特殊点的位置等进行逐项判断求解即可.
【详解】解:A、由图象知,当时,,故选项A错误,不符合题意;
B、∵图象的开口向下,与y轴的正半轴相交,其对称轴为直线,图象经过点,
∴,,,,
∴,故选项B正确,符合题意;
C、,故选项C错误,不符合题意;
D、∵当时,y随x的增大而增大,当时,y随x的增大而减小,
∴当时,y随x的增大而增大是错误的,故选项D不符合题意;
故选:B.
7.(23-24·山东青岛·一模)如图,已知抛物线()的顶点坐标是,与x轴的两个交点是A,B,其中点B的坐标是,则下列结论正确的是:( )
A. B.
C.点A的坐标为 D.
【答案】D
【分析】依据题意,由抛物线开口向上,从而,又顶点为,故对称轴是直线,从而,再结合抛物线交轴于负半轴,则故可判断;又抛物线与轴有两个交点,判别式,故可判断;又对称轴是直线,,从而,故可判断C;又,再结合当时,,从而可以判断D.本题主要考查了二次函数的图象与性质,解题时要熟练掌握并能灵活运用是关键.
【详解】解:抛物线开口向上,
.
顶点为,
对称轴是直线.
.
又抛物线交轴于负半轴,
.
,故A错误.
又∵抛物线与轴有两个交点,
判别式,故B错误.
对称轴是直线,,
,故C错误.
,
又当时,,
.
,故D正确.
故选:D.
8.(23-24九年级·湖北黄冈·期中)在平面直角坐标系xOy中,O为坐标原点,抛物线 的对称轴为 与x轴的一个交点位于,两点之间.下列结论:其中正确的是( )
A. B.
C. D.若、为方程 的两个根,则
【答案】D
【分析】由对称轴得,,;抛物线与x轴的一个交点位于,两点之间,对称性知另一个交点在,之间,得 ,,于是,进一步推知,由根与系数关系知
【详解】解:依题意可画出草图:
因为对称轴,,所以,故选项A错误;
抛物线与x轴的一个交点位于,两点之间,对称轴为,故知另一个交点在,之间,
因为,所以抛物线开口向下,
故时,, 时,,
故 故选项B错误;
∴,得,故C错误;
由,,知,
∵,为方程的两个根,
∴
∴,故D正确;
故选:D
【点睛】本题考查二次函数图象性质,一元二次方程根与系数关系,不等式变形,掌握函数图象性质,注意利用特殊点是解题的关键.
9.(23-24·浙江·一模)抛物线的顶点为,且经过点,其部分图象如图所示,则下列结论正确的是( )
A.若抛物线经过点,则必过点
B.若点和都在抛物线上,则
C.
D.
【答案】D
【分析】本题主要考查了抛物线图象与系数的关系以及一元二次方程的根与系数的关系,根据抛物线的开口方向和对称轴的位置可判断、、的符号,然后再根据两根关系和抛物线与的交点情况逐项判定即可,熟练掌握抛物线图象与系数的关系是解题的关键.
【详解】解:A、由图象可知,抛物线对称轴为直线,若经过点,则经过点,故选项不符合题意;
B、由图象可知,图象开口向下,
∴,
由离对称轴越近的值越大,
∵,
∴,故选项不符合题意;
C、∵抛物线对称轴为直线,且过点,
∴与的另一个交点为,
∴,故选项不符合题意;
D、∵抛物线的顶点为,且经过点,,
∴代入抛物线得:,则,
,则,
由得:,故选项符合题意;
故选:D.
10.(23-24九年级·四川绵阳·阶段练习)已知抛物线,且,.则下列结论中错误的是( )
A.点和在抛物线上 B.抛物线与x轴负半轴必有一个交点
C. D.当时,y有最小值为8a
【答案】C
【分析】本题主要考查了二次函数的图象和性质,根据,解方程,然后结合二次函数图象性质判断即可.
【详解】∵当时,,当时,,
∴点和在抛物线上,故选项A正确,不符合题意;
联立,解得,
∵,
∴,
∵
∴函数开口向下,对称轴在y轴左侧,
∴抛物线与x轴负半轴必有一个交点,故B正确,不符合题意;
∵,,,
∴,故C不正确,符合题意;
∵函数开口向下,对称轴在y轴左侧,
∴当时,y随x增大而减小,
∴当时,y有最小值,故D正确,不符合题意;
故选:C.
11.(23-24九年级·全国·竞赛)已知开口向上的抛物线经过点,且,则的取值范围是( ).
A. B.
C. D.
【答案】C
【分析】本题考查了二次函数的图象与性质,一元二次方程根与系数的关系,利用完全平方公式的变形进行计算,由抛物线过点得出,结合以及抛物线开口向上得出,由题意得出、是一元二次方程的两根,由一元二次方程根与系数的关系得出,再由,计算即可得出答案.
【详解】解:抛物线经过点,
,
,
由得,
抛物线开口向上,
,
,
解得,
抛物线经过点,
、是一元二次方程的两根,
,
,
,
故选:C.
12.(23-24九年级·河南郑州·期末)如图,二次函数的图象与轴分别交于A、B两点,与轴交于点,点的坐标为,下列结论中正确的是( )
A. B. C. D.
【答案】C
【分析】本题考查二次函数的图象和性质,根据图象获取信息,根据二次函数的性质,进行判断即可.掌握二次函数的图象和性质,是解题的关键.
【详解】解:∵抛物线的开口向下,对称轴为,交轴于正半轴,
∴,
∴,故选项A错误;
∵图象经过点,
∴,故选项B错误;
由图象可知当时,,故选项C正确;
∵对称轴为,
∴与时的函数值相同,即:,故选项D错误;
故选:C.
【题型2 二次函数图象与系数的关系的多结论问题】
13.(23-24·四川成都·模拟预测)如图,抛物线与x轴交于点,,
与y轴交于点C.有下列说法:①;②抛物线的对称轴为直线;③当时,;④当时,y的值随x值的增大而减小;⑤(m为任意实数).其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】本题主要考查了抛物线的图象与系数的关系、抛物线的性质等知识点,熟练掌握抛物线的相关知识是解题的关键.
根据抛物线开口向上可得,对称轴为可得通时判定②;与y轴交于负半轴可得,即可判定①;根据和点可得抛物线的对称轴为直线,即可判断②;由图象可知,当时,可推出③错误;根据函数图象即可判断④;当时,函数有最小值,进而判断⑤.
【详解】解:∵抛物线开口向上,
∴,
∵抛物线与x轴交于点,,
∴对称轴为直线,故②正确;
∵,
∴,
∵抛物线与y轴的交点在负半轴上,
∴,
∴,故①错误;
由图象可知,当时,,
∴当时,,故③错误;
由图象可知,当时,y的值随x值的增大而增大,故④错误;
∵且抛物线的对称轴为直线,
∴当时,函数有最小值,
∴当m为任意实数时,,
∴,故⑤正确.
综上所述,说法正确的是②⑤,共2个.
故选B.
14.(23-24九年级·黑龙江大庆·期末)如图,二次函数的图象与轴交于点,与轴交于点,对称轴为直线,下列四个结论:①;②;③若实数,则;④若,则,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】此题考查了二次函数的图象和性质,数形结合是解题的关键,利用开口方向和对称轴的位置即可判断①,利用对称轴和特殊点的函数值即可判断②,利用二次函数的最值即可判断③,求出,进一步得到,又根据得到,即可判断④.
【详解】解:①函数图象开口方向向上,
;
对称轴在轴右侧,
、异号,
,
∵抛物线与轴交点在轴负半轴,
,
,故①错误;
②二次函数的图象与轴交于点,与轴交于点,对称轴为直线,
,
,
时,,
,
,
,故②正确;
③对称轴为直线,,
最小值,
∵,
∴,
∴,
故③正确;
④,
∴根据抛物线与相应方程的根与系数的关系可得,
,
,
,
,
,
,
故④正确;
综上所述,正确的有②③④,
故选:C
15.(23-24·黑龙江绥化·中考真题)二次函数的部分图象如图所示,对称轴为直线,则下列结论中:
① ②(m为任意实数) ③
④若、是抛物线上不同的两个点,则.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】本题考查了二次函数的图象与性质,根据抛物线的开口方向,对称轴可得,即可判断①,时,函数值最大,即可判断②,根据时,,即可判断③,根据对称性可得即可判段④,即可求解.
【详解】解:∵二次函数图象开口向下
∴
∵对称轴为直线,
∴
∴
∵抛物线与轴交于正半轴,则
∴,故①错误,
∵抛物线开口向下,对称轴为直线,
∴当时,取得最大值,最大值为
∴(m为任意实数)
即,故②正确;
∵时,
即
∵
∴
即
∴,故③正确;
∵、是抛物线上不同的两个点,
∴关于对称,
∴即故④不正确
正确的有②③
故选:B
16.(23-24九年级·云南昆明·期末)如图,已知二次函数的图象与轴交于点,与轴的交点在和之间(不包括这两点),对称轴为直线,下列结论:①;②;③;④;其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】本题考查了二次函数图象与系数的关系.二次函数系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点位置确定.利用数形结合的思想是解题的关键.根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【详解】解:①∵图象与x轴交于点,对称轴为直线,
∴图象与x轴的另一个交点为,
∴当时,,
∴,故①错误;
②∵函数开口方向向上,
∴,
∵抛物线与y轴交点在和之间,对称轴为直线,
∴顶点纵坐标要小于,
∴,且,
∴,故②正确;
③∵图象与y轴的交点在和之间,
∴,
∵图象与x轴交于点和,
∴的两根为和3,
由韦达定理可知:,
∴,
∴,
∴,故③正确;
④∵对称轴为直线为,
∴,
∵,,
∴,故④正确.
综上所述,正确的有②③④,
故选:C.
17.(23-24九年级·湖北宜昌·阶段练习)如图,己知开口向下的抛物线与x轴交于点,对称轴为直线.则下列结论:①;②;③;④抛物线上有两点和,若且,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】本题考查二次函数图象与系数的关系,二次函数的性质,根据抛物线开口方向,对称轴位置,抛物线与y轴交点位置判断①;由抛物线的对称性可判断②;由二次函数的对称轴为可判断③;由二次函数的性质可判断④.
【详解】解:∵抛物线开口向下,
∴,
∵抛物线交y轴于正半轴,
∴,
∵,
∴,
∴,故①正确;
∵抛物线对称轴为直线时,,
∴时,,
∴,故②正确;
∵对称轴为直线,
∴
∴,
∴,
故③正确;
∵抛物线开口向下,对称轴为直线,
若且,则点到对称轴的距离小于到直线的距离,
∴,故④不正确.
故选:C.
18.(23-24九年级·云南·期末)二次函数的部分图象如图,图象过点下列结论:①;②;③;④;⑤若顶点坐标为,则方程没有实数根.其中正确的结论有( )
A.个 B.个 C.个 D.个
【答案】A
【分析】本题主要考查二次函数与系数相关代数式的判断问题,会利用对称轴求与的关系,以及二次函数与方程之间的转换,掌握根的判别式的熟练运用,是解题的关键.
由抛物线的开口方向判断,将点代入,得,由图象可得对称轴为,可得,代入上式可得,再将五个结论分别分析即可由得到答案.
【详解】解:将点代入,
即,
∵图象可得二次函数的对称轴为,开口向下,
∴,,
即,
将代入,
可得.
①∵、,
∴,,
∴,
∴,
故①正确.
②∵,
∴,
故②正确.
③∵、,
∴,,
∵,
∴,
∴,
故③错误.
④∵、,
故,
∵,
∴,
∴,
故④错误.
⑤将代入,即,
再将、代入上式,
化简可得,
∴,,
将,,,代入则方程中,
即,
根据根的判别式,
可得方程没有两个不相同的实数根,
故⑤错误.
综上作述,正确的结论有两个,
故选.
19.(23-24·新疆乌鲁木齐·一模)如图,二次函数的图象与x轴负半轴交于,顶点坐标为,有以下结论:①;②;③若点,,,均在函数图象上,则;④对于任意m都有;⑤点M,N是抛物线与x轴的两个交点,若在x轴下方的抛物线上存在一点P,使得,则a的范围为.其中结论正确的有( )
A.5个 B.4个 C.3个 D.2个
【答案】B
【分析】本题主要考查了二次函数图象与系数之间的关系,二次函数图象的性质等等,根据抛物线开口方向可判断a的取值范围,由对称轴的位置及a的符号可判断b的符合,由抛物线与y轴交点位置可判断c的符号,从而可判断①错误;由图象过 及对称轴可判断②正确;由抛物线开口向上,离对称轴水平距离越大,y越大,可判断③正确;根据函数开口向上,在对称轴处有最小值,即可判断④正确;由M,N到对称轴的距离为,当抛物线的顶点到x轴的距离不小于时,在x轴下方的抛物线上存在点P,使得,即,得可判断⑤正确.
【详解】解:∵函数开口向上,与y轴交于负半轴,
∴,,
∵顶点坐标为,即对称轴为直线,
,
,
,故①错误;
由图可知,当时,,
,即,故②正确;
抛物线开口向上,
∴离对称轴距离越大,y越大,
又∵,,,
∴;故③正确;
∵函数开口向上,
∴在对称轴处函数有最小值,
∴,即故④正确;
由题意可知:M,N到对称轴的距离为,
当抛物线的顶点到x轴的距离刚好等于时,此时顶点与M、N两个点恰好构成等腰直角三角形,
∴当抛物线的顶点到x轴的距离大于等于时在x轴下方的抛物线上存在点P,使得,
∴,
把代入解析式得,
∴,
,
,
解得:,故⑤正确;
故选:B.
20.(23-24九年级·山东烟台·期中)已知二次函数,图象的一部分如图所示,该函数图象经过点,顶点坐标为.对于下列结论:①;②;③若关于x的一元二次方程无实数根,则;④)(其中)﹔⑤若和均在该函数图象上,且,则.其中正确结论有( )
A.②③④ B.②③⑤ C.②③ D.④⑤
【答案】A
【分析】本题考查了二次函数的图象与性质、二次函数图象与直线交点问题,掌握二次函数图象与系数关系,二次函数的性质,利用数形结合思想解题是关键.
根据抛物线与轴的一个交点以及其对称轴,求出抛物线与轴的另一个交点,利用待定系数法求函数解析式,再根据抛物线开口朝下,可得,进而可得,,再结合二次函数的图象和性质逐条判断即可.
【详解】解:抛物线开口方向向下,
,
抛物线的对称轴为直线,
∴
∴
∵抛物线与抛物线与轴交点在正半轴上,
∴,
,故①错误;
抛物线的对称轴为直线,且抛物线与轴的一个交点坐标为,
抛物线与轴的另一个交点坐标为,
把代入,可得:,故②正确;
∵关于x的一元二次方程无实数根,
∴二次函数的图象与直线无交点,
∵抛物线的顶点坐标为,抛物线开口方向向下,
∴,故③正确;
,
,
,
又,,
,
即(其中,故④正确;
抛物线的对称轴为直线,且抛物线开口朝下,
可知二次函数,在时,随的增大而减小,
,
,故⑤错误,
正确的有②③④,
故选:A.
21.(23-24·山东滨州·一模)如图,抛物线经过点,顶点为,且抛物线与y轴的交点B在和之间(不含端点),小明同学得出了下列结论:①当时,;②a的取范围为;③当时,的面积为.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
【答案】B
【分析】本题考查了二次函数的图象和性质,三角形面积等知识点, ①据抛物线的对称性可得:抛物线与x轴的另一个交点坐标为,再结合抛物线的性质可判断结论①;②代入,得出,由点B在与之间(不含端点)可得出a的取值范围,进而即可判断②;③化成顶点式,得抛物线的顶点为,设抛物线对称轴交x轴于H,利用,将a值代入即可判断③;熟练掌握函数图象与系数的关系是解决此题的关键.
【详解】①∵抛物线经过点,顶点为,
∴抛物线的对称轴为直线,
∴抛物线与x轴的另一个交点坐标为,
∵抛物线的开口向上,
∴当时,;
故①正确.
②将代入得
,
解得:,
∴,
∵点B在与之间(不含端点),
∴,
∴,
故②错误;
③∵
∴抛物线的顶点为,
设抛物线对称轴交x轴于H,如图,
则,
∴,
∵,
∴,
∴
,
∵,
∴,
故③正确,
综上所述:正确的为①③;
故选:B.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
22.(23-24九年级·湖北武汉·期末)已知二次函数(,为常数且)经过,且,下列结论: ; ;若关于的方程有整数解,则符合条件的的值有个;当时,二次函数的最大值为,则.
其中一定正确的有 .(填序号即可)
【答案】/////
【分析】本题考查了二次函数的性质,当时,,则,根据得,根据,得,根据得,则,即可判断正确,根据,得,即可得点在轴的下方,根据抛物线的对称轴为直线,,得抛物线与直线交点的横坐标为整数的有,则关于x的方程有整数解,则符合条件的的值有个,故正确;根据抛物线对称轴为直线,与轴的交点为,得抛物线过,根据当时,二次函数的最大值为得或,即可得;熟练掌握二次函数的性质是解题的关键.
【详解】解:二次函数,当时,,
∴,
∵,
∴,
∵,,
∴,
∵,
∴,
,
∴正确,
∵,,
∴,
∴点在轴的下方,
∵抛物线的对称轴为直线,,,
∴抛物线与直线交点的横坐标为整数的有,
∴关于的方程有整数解,则符合条件的的值有个,
故正确;
∵抛物线对称轴为直线,与轴的交点为,
∴抛物线过,
∵当时,二次函数的最大值为,且,
∴,
∴,
故错误,
综上,正确,
故答案为:.
23.(23-24九年级·湖北·阶段练习)已知抛物线 (a,b,c均为常数)的顶点坐标为 其中,与x轴的一个交点位于和之间,则下列结论:
① ;
②;
③若该抛物线经过点,,则
④若关于x的一元二次方程 无实数根,则.
其中正确的结论是 .(只填序号)
【答案】①③/③①
【分析】本题考查了抛物线的性质,抛物线与一元二次方程的关系,熟练掌握性质是解题的关键,根据顶点坐标,根的判别式,点到对称轴的距离大小比较计算判断即可.
【详解】∵抛物线 (a,b,c均为常数)的顶点坐标为 其中,与x轴的一个交点位于和之间,
∴,,,,
∴,,,
∴,
故①正确;②错误;
∵,,距离对称轴越远,函数值越小,
∴,
故③正确;
∵关于x的一元二次方程 无实数根,
∴,
∴,
即
∵,
则.
故④错误;
故答案为:①③.
24.(23-24九年级·福建福州·阶段练习)如图所示,二次函数的图像的对称轴是直线,且经过点.有下列结论:①;②;③(为常数);④和时函数值相等;⑤若,,在该函数图像上,则;⑥.其中错误的结论是 (填序号).
【答案】①⑤
【分析】根据二次函数图像与性质逐项判断即可得到答案.
【详解】解:∵抛物线开口向下,
∴,
∵抛物线对称轴是直线,
∴,即,
∴,
∵经过点,
∴,
∴,故①错误;
∵抛物线与轴有两个交点,
∴,故②正确;
∵当时,函数取得最大值,最大值为,
∴当时,,
∴,故③正确;
∵抛物线的对称轴是直线,
∴直线和直线与对称轴距离相等,则和时的函数值相等,故④正确;
∵抛物线的对称轴是直线,且开口向下,
∴离对称轴越近,函数值越大,
∴,故⑤错误;
当时,,
∴,
∴,故⑥正确;
故答案为:①⑤.
【点睛】本题考查二次函数图像与性质,灵活掌握利用二次函数图像与性质解决代数式符号问题的解法是解决问题的关键.
25.(23-24九年级·广西贵港·期末)如图,抛物线与轴正半轴交于两点,轴负半轴交于点.若点,则下列结论中: ; ; 与是抛物线上两点,若,则;若抛物线的对称轴是直线,为任意实数,则;若则其中正确结论的个数共有 个.
【答案】4
【分析】根据图象得出,,可判断;再由图象可得对称轴在直线右侧,可得,可判断;再根据二次函数在轴右侧的增减性,判断;根据抛物线对称轴为直线,得出,再利用作差法判断;最后根据,则点的横坐标大于0且小于等于1,得出当时,,当时,,变形为,代入,可得,结合的符号可判断.
【详解】解:由抛物线图象可知,抛物线开口向下,与轴交于负半轴,对称轴在轴右侧,
,
,
,故正确;
抛物线与轴正半轴交于两点,点,
对称轴在直线右侧,
即,
,
,
,故正确;
与是抛物线上两点,由图象可得抛物线在上,随的增大而增大,在上, 随的增大而减小,
不一定成立,故错误;
若抛物线的对称轴是直线,
,即,
,
,故正确;
由得,,
当时,,
当时,,
,
,
整理得,
,
,,
,故正确;
综上所述,正确的有4个,
故答案为:4.
【点睛】本题考查了二次函数的图象和性质,解题的关键是能根据图象得出二次函数表达式各项系数的符号.
26.(23-24九年级·湖北武汉·阶段练习)如图,抛物线与x轴交于点,,交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①;②(m为任意实数);③若点P为对称轴上的动点,则有最大值,最大值为;④若m是方程的一个根,则一定有成立.其中正确的序号有 .
【答案】①②④
【分析】利用待定系数法,二次函数的相纸,两点之间线段最短逐一判断即可.
【详解】解:抛物线开口向下,
,
抛物线与x轴交于点,,
对称轴为直线,
,
抛物线交y轴的正半轴,
,
,故①正确;
对称轴为直线,开口向下,
时,y有最大值,最大值为,
(m为任意实数)
即,故②正确;
对称轴交y轴的正半轴于点C,
,
由对称性可知,
,故③不正确;
抛物线与x轴交于点,
,
,
,
,
,
m是方程的一个根,
,
当时,,
当时,,
若m是方程的一个根,则一定有成立,故④正确;
故答案为:①②④.
【点睛】本题考查二次函数图象和性质,解决本题关键是运用二次函数图像上点的坐标特征、抛物线与x轴交点进行计算.
27.(23-24九年级·江西上饶·期末)如图,已知抛物线与x轴交于A、B两点,与y轴交于点C,顶点为D,其中点B坐标为(3,0),顶点D的横坐标为1,轴,垂足为E,下列结论:①当时,y随x增大而减小;②;③;④;⑤当时,.其中结论正确的有 .(填序号)(多填错填倒扣一分)
【答案】③④⑤
【分析】①根据抛物线开口向下,对称轴为直线x=1,判定当x<1时,y随x增大而增大;②根据a<0,, 得到b=-2a,代入a+b=a-2a=-a>0;③x=3时,y=9a+3b+c=0,b=-2a,得到9a+3b+c=9a-6a+c=3a+c=0,根据,a<0,得到b>0,推出3a+b+c>0;④根据3a+c=0,得到c=-3a,推出 ;⑤根据抛物线与x轴交于A、B两点,其中点B坐标为(3,0),对称轴为直线x=1,得到A(-1,0)设抛物线解析式为,推出当时,-3a>2.
【详解】①当时,y随x增大而减小,
∵抛物线顶点D的横坐标为1,
∴对称轴为直线x=1,
∵抛物线开口向下,
∴当时,y随x增大而增大,
∴不正确;
②,
∵,a<0,
∴b=-2a>0,
∴a+b=a-2a=-a>0,
∴不正确;
③,
∵x=3时,y=9a+3b+c=0,b=-2a,
∴9a+3b+c=9a-6a+c=3a+c=0,
∵b>0,
∴3a+b+c>0,
∴正确;
④,
∵b=-2a,3a+c=0,
∴c=-3a,
,
∴正确;
⑤当时,,
∵抛物线与x轴交于A、B两点,其中点B坐标为(3,0),对称轴为直线x=1,
∴A(-1,0)
∴设抛物线解析式为,
当时,-3a>2,
∴正确.
故答案为,③④⑤.
【点睛】本题考查了二次函数图象与系数的关系,解决此类问题的关键是熟练掌握图象开口与a的关系,图象与y轴交点与c的关系,对称轴与a、b的关系,图象与x轴的交点特征.
28.(23-24九年级·重庆·期末)如图,函数的图象过点和,下列判断:
①;
②;
③;
④和处的函数值相等.
其中正确的是 (只填序号).
【答案】①③④
【分析】根据抛物线开口方向,对称轴以及与轴的交点即可判断①;根据、的符号得出,即可得到,根据时,得到,即可得到,即可判断②;根据抛物线与一元二次方程的关系即可判断③;根据抛物线的对称性即可判断④.
【详解】解:抛物线开口向下,
,
抛物线交轴于正半轴,
,
,
,
,故①正确,
,,
,
,
时,,则,
,
,故②错误,
的图象过点和,
方程的根为,,
方程的根为,
,
,故③正确;
的图象过点和,
抛物线的对称轴为直线,
,
和处的函数值相等,故④正确,
故答案为:①③④.
【点睛】本题考查了二次函数图象与系数的关系:对于二次函数,二次项系数决定抛物线的开口方向:当时,抛物线向上开口;当时,抛物线向下开口;一次项系数和二次项系数共同决定对称轴的位置:当与同号时(即,对称轴在轴左;当与异号时(即,对称轴在轴右;常数项决定抛物线与轴交点:抛物线与轴交于;△决定抛物线与轴交点个数:△时,抛物线与轴有2个交点;△时,抛物线与轴有1个交点;△时,抛物线与轴没有交点.
29.(23-24九年级·广东广州·期末)抛物线y=ax2+bx+c中,b=4a,它的图象如图,有以下结论:①c>0;②a+b+c>0;③a﹣b+c>0 ④b2﹣4ac<0;⑤abc<0;⑥4a>c;其中正确的为 (填序号).
【答案】①②⑥.
【分析】由抛物线的开口向上可知a>0,与y轴的交点为在y轴的正半轴上可得c>0,由此判定①正确;由4a-b和对称轴为x=- =-2,则a、b同号,即b>0,然后即可判定⑤错误;由抛物线与x轴有两个交点得到b2-4ac>0,由此判定④错误;当x=1时,y=a+b+c>0,由此判定②正确;当x=-1时,y=a-b+c<0,由此判定③错误;由a-b+c<0,而2a=b,可以推出cc,由此判定⑥正确
【详解】解:∵抛物线的开口向上,
∴a>0,
∵与y轴的交点为在y轴的正半轴上,
∴c>0,
∴①正确;
∵对称轴为x==﹣1,得2a=b,
∴a、b同号,即b>0,
∴abc>0,
∴⑤错误;
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴④错误;
当x=1时,y=a+b+C>0,
∴②正确;
当x=﹣1时,y=a﹣b+c<0,
∴③错误;
∵a﹣b+c<0,4a=b,
∴c<3a,
∴4a>c,
∴⑥正确.
故填空答案:①②⑥.
【点睛】本题考查了二次函数的图象与系数的关系,二次函数y=ax2+bx+c系数符号的确定以及灵活运用数形结合思想是解答本题的关键.
30.(23-24九年级·湖北武汉·阶段练习)已知二次函数的图象过点,,,且交轴的正半轴于点,下列结论: ; ;若直线与抛物线只有一个公共点,则;抛物线上的两点,,在的左边,若,则; ,请将所有正确的序号填在横线上 .
【答案】
【分析】本题考查了二次函数图象与系数的关系及二次函数的性质,抛物线与 轴的交点,抛物线的对称性等知识点,根据二次函数的图象进行逐项分析即可,灵活运用有关知识来分析是解题的关键.
【详解】∵图象过点,,,
∴抛物线对称轴为直线,,
∴与轴交于点,即有,故正确;
∵交轴的正半轴于点,
∴抛物线开口向下,
∴,,,则,故正确;
由抛物线对称轴为直线,
∴,则,
∴代入得:,
∴抛物线,直线与抛物线只有一个公共点,
∴,整理得:
∴,解得:,
∴直线,代入得:,
∴,故正确;
∵抛物线上的两点,,
∴,,
∴,
∵,,,
即,
∴,故错误;
∵,
∴错误,
∴正确;
故答案为:.
21世纪教育网(www.21cnjy.com)
【人教版】
考卷信息:
本套训练卷共30题,题型针对性较高,覆盖面广,选题有深度,可加强学生对二次函数图象与各项系数符号之间的关系的理解!
【题型1 二次函数图象与系数的关系的单结论问题】
1.(23-24·四川成都·模拟预测)如图,二次函数的图象与轴交于,两点,下列说法正确的是( )
A.
B.抛物线的对称轴是直线
C.当时,的值随值的增大而减小
D.
2.(23-24九年级·河南商丘·阶段练习)如图为抛物线的图象,A、B、C 为抛物线与坐标轴的交点,且,则下列关系中正确的是( )
A. B. C. D.
3.(23-24·湖北鄂州·模拟预测)如图,二次函数()的图象关于直线对称,则下列结论正确的是( )
A.
B.若抛物线与x轴交于,两点,则
C.
D.对任意实数t,总有
4.(23-24·广西钦州·三模)在平面直角坐标系中,二次函数的图像如图所示,以下结论中正确的是( )
A.
B.
C.
D.若为任意实数,则
5.(23-24·浙江温州·二模)已知二次函数的图象如图所示,则下列选项中错误的是( ).
A. B.的解为,
C. D.点在第三象限
6.(23-24九年级·湖北黄冈·期中)已知二次函数的图象如图所示,对称轴为直线,且经过点,下列结论中正确的是( )
A. B.
C. D.当时,y随x的增大而增大
7.(23-24·山东青岛·一模)如图,已知抛物线()的顶点坐标是,与x轴的两个交点是A,B,其中点B的坐标是,则下列结论正确的是:( )
A. B.
C.点A的坐标为 D.
8.(23-24九年级·湖北黄冈·期中)在平面直角坐标系xOy中,O为坐标原点,抛物线 的对称轴为 与x轴的一个交点位于,两点之间.下列结论:其中正确的是( )
A. B.
C. D.若、为方程 的两个根,则
9.(23-24·浙江·一模)抛物线的顶点为,且经过点,其部分图象如图所示,则下列结论正确的是( )
A.若抛物线经过点,则必过点
B.若点和都在抛物线上,则
C.
D.
10.(23-24九年级·四川绵阳·阶段练习)已知抛物线,且,.则下列结论中错误的是( )
A.点和在抛物线上 B.抛物线与x轴负半轴必有一个交点
C. D.当时,y有最小值为8a
11.(23-24九年级·全国·竞赛)已知开口向上的抛物线经过点,且,则的取值范围是( ).
A. B.
C. D.
12.(23-24九年级·河南郑州·期末)如图,二次函数的图象与轴分别交于A、B两点,与轴交于点,点的坐标为,下列结论中正确的是( )
A. B. C. D.
【题型2 二次函数图象与系数的关系的多结论问题】
13.(23-24·四川成都·模拟预测)如图,抛物线与x轴交于点,,
与y轴交于点C.有下列说法:①;②抛物线的对称轴为直线;③当时,;④当时,y的值随x值的增大而减小;⑤(m为任意实数).其中正确的有( )
A.1个 B.2个 C.3个 D.4个
14.(23-24九年级·黑龙江大庆·期末)如图,二次函数的图象与轴交于点,与轴交于点,对称轴为直线,下列四个结论:①;②;③若实数,则;④若,则,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
15.(23-24·黑龙江绥化·中考真题)二次函数的部分图象如图所示,对称轴为直线,则下列结论中:
① ②(m为任意实数) ③
④若、是抛物线上不同的两个点,则.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
16.(23-24九年级·云南昆明·期末)如图,已知二次函数的图象与轴交于点,与轴的交点在和之间(不包括这两点),对称轴为直线,下列结论:①;②;③;④;其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
17.(23-24九年级·湖北宜昌·阶段练习)如图,己知开口向下的抛物线与x轴交于点,对称轴为直线.则下列结论:①;②;③;④抛物线上有两点和,若且,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
18.(23-24九年级·云南·期末)二次函数的部分图象如图,图象过点下列结论:①;②;③;④;⑤若顶点坐标为,则方程没有实数根.其中正确的结论有( )
A.个 B.个 C.个 D.个
19.(23-24·新疆乌鲁木齐·一模)如图,二次函数的图象与x轴负半轴交于,顶点坐标为,有以下结论:①;②;③若点,,,均在函数图象上,则;④对于任意m都有;⑤点M,N是抛物线与x轴的两个交点,若在x轴下方的抛物线上存在一点P,使得,则a的范围为.其中结论正确的有( )
A.5个 B.4个 C.3个 D.2个
20.(23-24九年级·山东烟台·期中)已知二次函数,图象的一部分如图所示,该函数图象经过点,顶点坐标为.对于下列结论:①;②;③若关于x的一元二次方程无实数根,则;④)(其中)﹔⑤若和均在该函数图象上,且,则.其中正确结论有( )
A.②③④ B.②③⑤ C.②③ D.④⑤
21.(23-24·山东滨州·一模)如图,抛物线经过点,顶点为,且抛物线与y轴的交点B在和之间(不含端点),小明同学得出了下列结论:①当时,;②a的取范围为;③当时,的面积为.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
22.(23-24九年级·湖北武汉·期末)已知二次函数(,为常数且)经过,且,下列结论: ; ;若关于的方程有整数解,则符合条件的的值有个;当时,二次函数的最大值为,则.
其中一定正确的有 .(填序号即可)
23.(23-24九年级·湖北·阶段练习)已知抛物线 (a,b,c均为常数)的顶点坐标为 其中,与x轴的一个交点位于和之间,则下列结论:
① ;
②;
③若该抛物线经过点,,则
④若关于x的一元二次方程 无实数根,则.
其中正确的结论是 .(只填序号)
24.(23-24九年级·福建福州·阶段练习)如图所示,二次函数的图像的对称轴是直线,且经过点.有下列结论:①;②;③(为常数);④和时函数值相等;⑤若,,在该函数图像上,则;⑥.其中错误的结论是 (填序号).
25.(23-24九年级·广西贵港·期末)如图,抛物线与轴正半轴交于两点,轴负半轴交于点.若点,则下列结论中: ; ; 与是抛物线上两点,若,则;若抛物线的对称轴是直线,为任意实数,则;若则其中正确结论的个数共有 个.
26.(23-24九年级·湖北武汉·阶段练习)如图,抛物线与x轴交于点,,交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①;②(m为任意实数);③若点P为对称轴上的动点,则有最大值,最大值为;④若m是方程的一个根,则一定有成立.其中正确的序号有 .
27.(23-24九年级·江西上饶·期末)如图,已知抛物线与x轴交于A、B两点,与y轴交于点C,顶点为D,其中点B坐标为(3,0),顶点D的横坐标为1,轴,垂足为E,下列结论:①当时,y随x增大而减小;②;③;④;⑤当时,.其中结论正确的有 .(填序号)(多填错填倒扣一分)
28.(23-24九年级·重庆·期末)如图,函数的图象过点和,下列判断:
①;
②;
③;
④和处的函数值相等.
其中正确的是 (只填序号).
29.(23-24九年级·广东广州·期末)抛物线y=ax2+bx+c中,b=4a,它的图象如图,有以下结论:①c>0;②a+b+c>0;③a﹣b+c>0 ④b2﹣4ac<0;⑤abc<0;⑥4a>c;其中正确的为 (填序号).
30.(23-24九年级·湖北武汉·阶段练习)已知二次函数的图象过点,,,且交轴的正半轴于点,下列结论: ; ;若直线与抛物线只有一个公共点,则;抛物线上的两点,,在的左边,若,则; ,请将所有正确的序号填在横线上 .21世纪教育网(www.21cnjy.com)
专题22.6 二次函数的图象与系数的关系专项训练(30题)
【人教版】
考卷信息:
本套训练卷共30题,题型针对性较高,覆盖面广,选题有深度,可加强学生对二次函数图象与各项系数符号之间的关系的理解!
【题型1 二次函数图象与系数的关系的单结论问题】
1.(23-24·四川成都·模拟预测)如图,二次函数的图象与轴交于,两点,下列说法正确的是( )
A.
B.抛物线的对称轴是直线
C.当时,的值随值的增大而减小
D.
【答案】C
【分析】本题主要考查了二次函数的图象与性质,根据图象与y轴交点即可判定,再利用二次函数的对称性和与轴交点求出对称轴,根据图象即可判断当时,图象位于对称轴右侧,随的增大而减小,再由当时,可得.
【详解】解:由图象可知:抛物线与y轴交于正半轴,
∴,A选项的结论不正确,不符合题意;
二次函数的图象与轴交于,两点,
∴对称轴为,故B选项的结论不正确,不符合题意;
由图象知:当时,图象位于对称轴右侧,随的增大而减小,故C选项的结论正确,符合题意;
当时,,故D选项的结论不正确,不符合题意.
故选:C.
2.(23-24九年级·河南商丘·阶段练习)如图为抛物线的图象,A、B、C 为抛物线与坐标轴的交点,且,则下列关系中正确的是( )
A. B. C. D.
【答案】D
【分析】根据以下知识点分析即可:①二次项系数决定抛物线的开口方向和大小:当时,抛物线向上开口;当时,抛物线向下开口;②一次项系数和二次项系数共同决定对称轴的位置:当与同号时(即,对称轴在轴左;当与异号时(即,对称轴在轴右.(简称:左同右异)③常数项决定抛物线与轴交点.抛物线与轴交于.此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确二次函数各项的系数和图形的关系.
【详解】解:,
,
又时,,
,
,
选项C不正确;
抛物线开口向上,
;
又,
,
选项A不正确;
,
,
又,
,
选项D正确;
,
时,,
,
又,
,
选项B不正确.
故选:D.
3.(23-24·湖北鄂州·模拟预测)如图,二次函数()的图象关于直线对称,则下列结论正确的是( )
A.
B.若抛物线与x轴交于,两点,则
C.
D.对任意实数t,总有
【答案】B
【分析】本题考查二次函数图象与系数的关系及抛物线与轴的交点,能根据所给函数图象得出,,的正负,再利用抛物线的对称性来求解,根据所给函数图象中抛物线的对称轴可得出,之间的等量关系,再结合抛物线与轴的交点情况可解决问题.
【详解】解:由图知开口向下,
,
与交于正半轴,
,
图象关于直线对称,
,
,
,A选项错误;
若抛物线与x轴交于,两点,
,则,故B选项正确;
,
,
由图知,当时,,
不成立,故C选项错误;
当时,有,故D选项错误.
故选:B.
4.(23-24·广西钦州·三模)在平面直角坐标系中,二次函数的图像如图所示,以下结论中正确的是( )
A.
B.
C.
D.若为任意实数,则
【答案】B
【分析】本题考查了二次函数的性质,根据二次函数的图象判断的符号,根据抛物线与轴的交点即可判断B,C选项,根据抛物线开口向上,对称轴为直线,得出最小值为,进而即可求解.
【详解】解:抛物线开口向上,则,
抛物线的对称轴为直线,则
∴,
抛物线与轴交于负半轴,则
∴,故A选项错误;
∵当时,,
∴
∴,故B正确
∵抛物线的对称轴为直线,和时,
∴,故C错误;
∵,对称轴为直线
∴若为任意实数,则,即,故D错误,
故选:B.
5.(23-24·浙江温州·二模)已知二次函数的图象如图所示,则下列选项中错误的是( ).
A. B.的解为,
C. D.点在第三象限
【答案】D
【分析】本题主要考查了二次函数图象的性质、不等式的性质等知识点,熟练掌握二次函数图象的性质成为解题的关键.
根据二次函数图象的性质逐项分析判断即可.
【详解】解:A、由图象可得:对称轴,即,即A选项正确,不符合题意;
B、由函数图象可知:的解为,另一个解为:,即B选项正确,不符合题意;
C、由函数图象可知:且,则有;又当时,,即,即,即C选项正确,不符合题意;
D、由意义可知:,则,又,则,可得点在第二象限,故D选项错误,符合题意.
故选D.
6.(23-24九年级·湖北黄冈·期中)已知二次函数的图象如图所示,对称轴为直线,且经过点,下列结论中正确的是( )
A. B.
C. D.当时,y随x的增大而增大
【答案】B
【分析】本题考查二次函数的图象与性质,能从图象中获取信息是解答的关键.根据图象的开口方向、与坐标轴的交点、对称轴位置、函数的增减性、特殊点的位置等进行逐项判断求解即可.
【详解】解:A、由图象知,当时,,故选项A错误,不符合题意;
B、∵图象的开口向下,与y轴的正半轴相交,其对称轴为直线,图象经过点,
∴,,,,
∴,故选项B正确,符合题意;
C、,故选项C错误,不符合题意;
D、∵当时,y随x的增大而增大,当时,y随x的增大而减小,
∴当时,y随x的增大而增大是错误的,故选项D不符合题意;
故选:B.
7.(23-24·山东青岛·一模)如图,已知抛物线()的顶点坐标是,与x轴的两个交点是A,B,其中点B的坐标是,则下列结论正确的是:( )
A. B.
C.点A的坐标为 D.
【答案】D
【分析】依据题意,由抛物线开口向上,从而,又顶点为,故对称轴是直线,从而,再结合抛物线交轴于负半轴,则故可判断;又抛物线与轴有两个交点,判别式,故可判断;又对称轴是直线,,从而,故可判断C;又,再结合当时,,从而可以判断D.本题主要考查了二次函数的图象与性质,解题时要熟练掌握并能灵活运用是关键.
【详解】解:抛物线开口向上,
.
顶点为,
对称轴是直线.
.
又抛物线交轴于负半轴,
.
,故A错误.
又∵抛物线与轴有两个交点,
判别式,故B错误.
对称轴是直线,,
,故C错误.
,
又当时,,
.
,故D正确.
故选:D.
8.(23-24九年级·湖北黄冈·期中)在平面直角坐标系xOy中,O为坐标原点,抛物线 的对称轴为 与x轴的一个交点位于,两点之间.下列结论:其中正确的是( )
A. B.
C. D.若、为方程 的两个根,则
【答案】D
【分析】由对称轴得,,;抛物线与x轴的一个交点位于,两点之间,对称性知另一个交点在,之间,得 ,,于是,进一步推知,由根与系数关系知
【详解】解:依题意可画出草图:
因为对称轴,,所以,故选项A错误;
抛物线与x轴的一个交点位于,两点之间,对称轴为,故知另一个交点在,之间,
因为,所以抛物线开口向下,
故时,, 时,,
故 故选项B错误;
∴,得,故C错误;
由,,知,
∵,为方程的两个根,
∴
∴,故D正确;
故选:D
【点睛】本题考查二次函数图象性质,一元二次方程根与系数关系,不等式变形,掌握函数图象性质,注意利用特殊点是解题的关键.
9.(23-24·浙江·一模)抛物线的顶点为,且经过点,其部分图象如图所示,则下列结论正确的是( )
A.若抛物线经过点,则必过点
B.若点和都在抛物线上,则
C.
D.
【答案】D
【分析】本题主要考查了抛物线图象与系数的关系以及一元二次方程的根与系数的关系,根据抛物线的开口方向和对称轴的位置可判断、、的符号,然后再根据两根关系和抛物线与的交点情况逐项判定即可,熟练掌握抛物线图象与系数的关系是解题的关键.
【详解】解:A、由图象可知,抛物线对称轴为直线,若经过点,则经过点,故选项不符合题意;
B、由图象可知,图象开口向下,
∴,
由离对称轴越近的值越大,
∵,
∴,故选项不符合题意;
C、∵抛物线对称轴为直线,且过点,
∴与的另一个交点为,
∴,故选项不符合题意;
D、∵抛物线的顶点为,且经过点,,
∴代入抛物线得:,则,
,则,
由得:,故选项符合题意;
故选:D.
10.(23-24九年级·四川绵阳·阶段练习)已知抛物线,且,.则下列结论中错误的是( )
A.点和在抛物线上 B.抛物线与x轴负半轴必有一个交点
C. D.当时,y有最小值为8a
【答案】C
【分析】本题主要考查了二次函数的图象和性质,根据,解方程,然后结合二次函数图象性质判断即可.
【详解】∵当时,,当时,,
∴点和在抛物线上,故选项A正确,不符合题意;
联立,解得,
∵,
∴,
∵
∴函数开口向下,对称轴在y轴左侧,
∴抛物线与x轴负半轴必有一个交点,故B正确,不符合题意;
∵,,,
∴,故C不正确,符合题意;
∵函数开口向下,对称轴在y轴左侧,
∴当时,y随x增大而减小,
∴当时,y有最小值,故D正确,不符合题意;
故选:C.
11.(23-24九年级·全国·竞赛)已知开口向上的抛物线经过点,且,则的取值范围是( ).
A. B.
C. D.
【答案】C
【分析】本题考查了二次函数的图象与性质,一元二次方程根与系数的关系,利用完全平方公式的变形进行计算,由抛物线过点得出,结合以及抛物线开口向上得出,由题意得出、是一元二次方程的两根,由一元二次方程根与系数的关系得出,再由,计算即可得出答案.
【详解】解:抛物线经过点,
,
,
由得,
抛物线开口向上,
,
,
解得,
抛物线经过点,
、是一元二次方程的两根,
,
,
,
故选:C.
12.(23-24九年级·河南郑州·期末)如图,二次函数的图象与轴分别交于A、B两点,与轴交于点,点的坐标为,下列结论中正确的是( )
A. B. C. D.
【答案】C
【分析】本题考查二次函数的图象和性质,根据图象获取信息,根据二次函数的性质,进行判断即可.掌握二次函数的图象和性质,是解题的关键.
【详解】解:∵抛物线的开口向下,对称轴为,交轴于正半轴,
∴,
∴,故选项A错误;
∵图象经过点,
∴,故选项B错误;
由图象可知当时,,故选项C正确;
∵对称轴为,
∴与时的函数值相同,即:,故选项D错误;
故选:C.
【题型2 二次函数图象与系数的关系的多结论问题】
13.(23-24·四川成都·模拟预测)如图,抛物线与x轴交于点,,
与y轴交于点C.有下列说法:①;②抛物线的对称轴为直线;③当时,;④当时,y的值随x值的增大而减小;⑤(m为任意实数).其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】本题主要考查了抛物线的图象与系数的关系、抛物线的性质等知识点,熟练掌握抛物线的相关知识是解题的关键.
根据抛物线开口向上可得,对称轴为可得通时判定②;与y轴交于负半轴可得,即可判定①;根据和点可得抛物线的对称轴为直线,即可判断②;由图象可知,当时,可推出③错误;根据函数图象即可判断④;当时,函数有最小值,进而判断⑤.
【详解】解:∵抛物线开口向上,
∴,
∵抛物线与x轴交于点,,
∴对称轴为直线,故②正确;
∵,
∴,
∵抛物线与y轴的交点在负半轴上,
∴,
∴,故①错误;
由图象可知,当时,,
∴当时,,故③错误;
由图象可知,当时,y的值随x值的增大而增大,故④错误;
∵且抛物线的对称轴为直线,
∴当时,函数有最小值,
∴当m为任意实数时,,
∴,故⑤正确.
综上所述,说法正确的是②⑤,共2个.
故选B.
14.(23-24九年级·黑龙江大庆·期末)如图,二次函数的图象与轴交于点,与轴交于点,对称轴为直线,下列四个结论:①;②;③若实数,则;④若,则,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】此题考查了二次函数的图象和性质,数形结合是解题的关键,利用开口方向和对称轴的位置即可判断①,利用对称轴和特殊点的函数值即可判断②,利用二次函数的最值即可判断③,求出,进一步得到,又根据得到,即可判断④.
【详解】解:①函数图象开口方向向上,
;
对称轴在轴右侧,
、异号,
,
∵抛物线与轴交点在轴负半轴,
,
,故①错误;
②二次函数的图象与轴交于点,与轴交于点,对称轴为直线,
,
,
时,,
,
,
,故②正确;
③对称轴为直线,,
最小值,
∵,
∴,
∴,
故③正确;
④,
∴根据抛物线与相应方程的根与系数的关系可得,
,
,
,
,
,
,
故④正确;
综上所述,正确的有②③④,
故选:C
15.(23-24·黑龙江绥化·中考真题)二次函数的部分图象如图所示,对称轴为直线,则下列结论中:
① ②(m为任意实数) ③
④若、是抛物线上不同的两个点,则.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】本题考查了二次函数的图象与性质,根据抛物线的开口方向,对称轴可得,即可判断①,时,函数值最大,即可判断②,根据时,,即可判断③,根据对称性可得即可判段④,即可求解.
【详解】解:∵二次函数图象开口向下
∴
∵对称轴为直线,
∴
∴
∵抛物线与轴交于正半轴,则
∴,故①错误,
∵抛物线开口向下,对称轴为直线,
∴当时,取得最大值,最大值为
∴(m为任意实数)
即,故②正确;
∵时,
即
∵
∴
即
∴,故③正确;
∵、是抛物线上不同的两个点,
∴关于对称,
∴即故④不正确
正确的有②③
故选:B
16.(23-24九年级·云南昆明·期末)如图,已知二次函数的图象与轴交于点,与轴的交点在和之间(不包括这两点),对称轴为直线,下列结论:①;②;③;④;其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】本题考查了二次函数图象与系数的关系.二次函数系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点位置确定.利用数形结合的思想是解题的关键.根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【详解】解:①∵图象与x轴交于点,对称轴为直线,
∴图象与x轴的另一个交点为,
∴当时,,
∴,故①错误;
②∵函数开口方向向上,
∴,
∵抛物线与y轴交点在和之间,对称轴为直线,
∴顶点纵坐标要小于,
∴,且,
∴,故②正确;
③∵图象与y轴的交点在和之间,
∴,
∵图象与x轴交于点和,
∴的两根为和3,
由韦达定理可知:,
∴,
∴,
∴,故③正确;
④∵对称轴为直线为,
∴,
∵,,
∴,故④正确.
综上所述,正确的有②③④,
故选:C.
17.(23-24九年级·湖北宜昌·阶段练习)如图,己知开口向下的抛物线与x轴交于点,对称轴为直线.则下列结论:①;②;③;④抛物线上有两点和,若且,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】本题考查二次函数图象与系数的关系,二次函数的性质,根据抛物线开口方向,对称轴位置,抛物线与y轴交点位置判断①;由抛物线的对称性可判断②;由二次函数的对称轴为可判断③;由二次函数的性质可判断④.
【详解】解:∵抛物线开口向下,
∴,
∵抛物线交y轴于正半轴,
∴,
∵,
∴,
∴,故①正确;
∵抛物线对称轴为直线时,,
∴时,,
∴,故②正确;
∵对称轴为直线,
∴
∴,
∴,
故③正确;
∵抛物线开口向下,对称轴为直线,
若且,则点到对称轴的距离小于到直线的距离,
∴,故④不正确.
故选:C.
18.(23-24九年级·云南·期末)二次函数的部分图象如图,图象过点下列结论:①;②;③;④;⑤若顶点坐标为,则方程没有实数根.其中正确的结论有( )
A.个 B.个 C.个 D.个
【答案】A
【分析】本题主要考查二次函数与系数相关代数式的判断问题,会利用对称轴求与的关系,以及二次函数与方程之间的转换,掌握根的判别式的熟练运用,是解题的关键.
由抛物线的开口方向判断,将点代入,得,由图象可得对称轴为,可得,代入上式可得,再将五个结论分别分析即可由得到答案.
【详解】解:将点代入,
即,
∵图象可得二次函数的对称轴为,开口向下,
∴,,
即,
将代入,
可得.
①∵、,
∴,,
∴,
∴,
故①正确.
②∵,
∴,
故②正确.
③∵、,
∴,,
∵,
∴,
∴,
故③错误.
④∵、,
故,
∵,
∴,
∴,
故④错误.
⑤将代入,即,
再将、代入上式,
化简可得,
∴,,
将,,,代入则方程中,
即,
根据根的判别式,
可得方程没有两个不相同的实数根,
故⑤错误.
综上作述,正确的结论有两个,
故选.
19.(23-24·新疆乌鲁木齐·一模)如图,二次函数的图象与x轴负半轴交于,顶点坐标为,有以下结论:①;②;③若点,,,均在函数图象上,则;④对于任意m都有;⑤点M,N是抛物线与x轴的两个交点,若在x轴下方的抛物线上存在一点P,使得,则a的范围为.其中结论正确的有( )
A.5个 B.4个 C.3个 D.2个
【答案】B
【分析】本题主要考查了二次函数图象与系数之间的关系,二次函数图象的性质等等,根据抛物线开口方向可判断a的取值范围,由对称轴的位置及a的符号可判断b的符合,由抛物线与y轴交点位置可判断c的符号,从而可判断①错误;由图象过 及对称轴可判断②正确;由抛物线开口向上,离对称轴水平距离越大,y越大,可判断③正确;根据函数开口向上,在对称轴处有最小值,即可判断④正确;由M,N到对称轴的距离为,当抛物线的顶点到x轴的距离不小于时,在x轴下方的抛物线上存在点P,使得,即,得可判断⑤正确.
【详解】解:∵函数开口向上,与y轴交于负半轴,
∴,,
∵顶点坐标为,即对称轴为直线,
,
,
,故①错误;
由图可知,当时,,
,即,故②正确;
抛物线开口向上,
∴离对称轴距离越大,y越大,
又∵,,,
∴;故③正确;
∵函数开口向上,
∴在对称轴处函数有最小值,
∴,即故④正确;
由题意可知:M,N到对称轴的距离为,
当抛物线的顶点到x轴的距离刚好等于时,此时顶点与M、N两个点恰好构成等腰直角三角形,
∴当抛物线的顶点到x轴的距离大于等于时在x轴下方的抛物线上存在点P,使得,
∴,
把代入解析式得,
∴,
,
,
解得:,故⑤正确;
故选:B.
20.(23-24九年级·山东烟台·期中)已知二次函数,图象的一部分如图所示,该函数图象经过点,顶点坐标为.对于下列结论:①;②;③若关于x的一元二次方程无实数根,则;④)(其中)﹔⑤若和均在该函数图象上,且,则.其中正确结论有( )
A.②③④ B.②③⑤ C.②③ D.④⑤
【答案】A
【分析】本题考查了二次函数的图象与性质、二次函数图象与直线交点问题,掌握二次函数图象与系数关系,二次函数的性质,利用数形结合思想解题是关键.
根据抛物线与轴的一个交点以及其对称轴,求出抛物线与轴的另一个交点,利用待定系数法求函数解析式,再根据抛物线开口朝下,可得,进而可得,,再结合二次函数的图象和性质逐条判断即可.
【详解】解:抛物线开口方向向下,
,
抛物线的对称轴为直线,
∴
∴
∵抛物线与抛物线与轴交点在正半轴上,
∴,
,故①错误;
抛物线的对称轴为直线,且抛物线与轴的一个交点坐标为,
抛物线与轴的另一个交点坐标为,
把代入,可得:,故②正确;
∵关于x的一元二次方程无实数根,
∴二次函数的图象与直线无交点,
∵抛物线的顶点坐标为,抛物线开口方向向下,
∴,故③正确;
,
,
,
又,,
,
即(其中,故④正确;
抛物线的对称轴为直线,且抛物线开口朝下,
可知二次函数,在时,随的增大而减小,
,
,故⑤错误,
正确的有②③④,
故选:A.
21.(23-24·山东滨州·一模)如图,抛物线经过点,顶点为,且抛物线与y轴的交点B在和之间(不含端点),小明同学得出了下列结论:①当时,;②a的取范围为;③当时,的面积为.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
【答案】B
【分析】本题考查了二次函数的图象和性质,三角形面积等知识点, ①据抛物线的对称性可得:抛物线与x轴的另一个交点坐标为,再结合抛物线的性质可判断结论①;②代入,得出,由点B在与之间(不含端点)可得出a的取值范围,进而即可判断②;③化成顶点式,得抛物线的顶点为,设抛物线对称轴交x轴于H,利用,将a值代入即可判断③;熟练掌握函数图象与系数的关系是解决此题的关键.
【详解】①∵抛物线经过点,顶点为,
∴抛物线的对称轴为直线,
∴抛物线与x轴的另一个交点坐标为,
∵抛物线的开口向上,
∴当时,;
故①正确.
②将代入得
,
解得:,
∴,
∵点B在与之间(不含端点),
∴,
∴,
故②错误;
③∵
∴抛物线的顶点为,
设抛物线对称轴交x轴于H,如图,
则,
∴,
∵,
∴,
∴
,
∵,
∴,
故③正确,
综上所述:正确的为①③;
故选:B.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
22.(23-24九年级·湖北武汉·期末)已知二次函数(,为常数且)经过,且,下列结论: ; ;若关于的方程有整数解,则符合条件的的值有个;当时,二次函数的最大值为,则.
其中一定正确的有 .(填序号即可)
【答案】/////
【分析】本题考查了二次函数的性质,当时,,则,根据得,根据,得,根据得,则,即可判断正确,根据,得,即可得点在轴的下方,根据抛物线的对称轴为直线,,得抛物线与直线交点的横坐标为整数的有,则关于x的方程有整数解,则符合条件的的值有个,故正确;根据抛物线对称轴为直线,与轴的交点为,得抛物线过,根据当时,二次函数的最大值为得或,即可得;熟练掌握二次函数的性质是解题的关键.
【详解】解:二次函数,当时,,
∴,
∵,
∴,
∵,,
∴,
∵,
∴,
,
∴正确,
∵,,
∴,
∴点在轴的下方,
∵抛物线的对称轴为直线,,,
∴抛物线与直线交点的横坐标为整数的有,
∴关于的方程有整数解,则符合条件的的值有个,
故正确;
∵抛物线对称轴为直线,与轴的交点为,
∴抛物线过,
∵当时,二次函数的最大值为,且,
∴,
∴,
故错误,
综上,正确,
故答案为:.
23.(23-24九年级·湖北·阶段练习)已知抛物线 (a,b,c均为常数)的顶点坐标为 其中,与x轴的一个交点位于和之间,则下列结论:
① ;
②;
③若该抛物线经过点,,则
④若关于x的一元二次方程 无实数根,则.
其中正确的结论是 .(只填序号)
【答案】①③/③①
【分析】本题考查了抛物线的性质,抛物线与一元二次方程的关系,熟练掌握性质是解题的关键,根据顶点坐标,根的判别式,点到对称轴的距离大小比较计算判断即可.
【详解】∵抛物线 (a,b,c均为常数)的顶点坐标为 其中,与x轴的一个交点位于和之间,
∴,,,,
∴,,,
∴,
故①正确;②错误;
∵,,距离对称轴越远,函数值越小,
∴,
故③正确;
∵关于x的一元二次方程 无实数根,
∴,
∴,
即
∵,
则.
故④错误;
故答案为:①③.
24.(23-24九年级·福建福州·阶段练习)如图所示,二次函数的图像的对称轴是直线,且经过点.有下列结论:①;②;③(为常数);④和时函数值相等;⑤若,,在该函数图像上,则;⑥.其中错误的结论是 (填序号).
【答案】①⑤
【分析】根据二次函数图像与性质逐项判断即可得到答案.
【详解】解:∵抛物线开口向下,
∴,
∵抛物线对称轴是直线,
∴,即,
∴,
∵经过点,
∴,
∴,故①错误;
∵抛物线与轴有两个交点,
∴,故②正确;
∵当时,函数取得最大值,最大值为,
∴当时,,
∴,故③正确;
∵抛物线的对称轴是直线,
∴直线和直线与对称轴距离相等,则和时的函数值相等,故④正确;
∵抛物线的对称轴是直线,且开口向下,
∴离对称轴越近,函数值越大,
∴,故⑤错误;
当时,,
∴,
∴,故⑥正确;
故答案为:①⑤.
【点睛】本题考查二次函数图像与性质,灵活掌握利用二次函数图像与性质解决代数式符号问题的解法是解决问题的关键.
25.(23-24九年级·广西贵港·期末)如图,抛物线与轴正半轴交于两点,轴负半轴交于点.若点,则下列结论中: ; ; 与是抛物线上两点,若,则;若抛物线的对称轴是直线,为任意实数,则;若则其中正确结论的个数共有 个.
【答案】4
【分析】根据图象得出,,可判断;再由图象可得对称轴在直线右侧,可得,可判断;再根据二次函数在轴右侧的增减性,判断;根据抛物线对称轴为直线,得出,再利用作差法判断;最后根据,则点的横坐标大于0且小于等于1,得出当时,,当时,,变形为,代入,可得,结合的符号可判断.
【详解】解:由抛物线图象可知,抛物线开口向下,与轴交于负半轴,对称轴在轴右侧,
,
,
,故正确;
抛物线与轴正半轴交于两点,点,
对称轴在直线右侧,
即,
,
,
,故正确;
与是抛物线上两点,由图象可得抛物线在上,随的增大而增大,在上, 随的增大而减小,
不一定成立,故错误;
若抛物线的对称轴是直线,
,即,
,
,故正确;
由得,,
当时,,
当时,,
,
,
整理得,
,
,,
,故正确;
综上所述,正确的有4个,
故答案为:4.
【点睛】本题考查了二次函数的图象和性质,解题的关键是能根据图象得出二次函数表达式各项系数的符号.
26.(23-24九年级·湖北武汉·阶段练习)如图,抛物线与x轴交于点,,交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①;②(m为任意实数);③若点P为对称轴上的动点,则有最大值,最大值为;④若m是方程的一个根,则一定有成立.其中正确的序号有 .
【答案】①②④
【分析】利用待定系数法,二次函数的相纸,两点之间线段最短逐一判断即可.
【详解】解:抛物线开口向下,
,
抛物线与x轴交于点,,
对称轴为直线,
,
抛物线交y轴的正半轴,
,
,故①正确;
对称轴为直线,开口向下,
时,y有最大值,最大值为,
(m为任意实数)
即,故②正确;
对称轴交y轴的正半轴于点C,
,
由对称性可知,
,故③不正确;
抛物线与x轴交于点,
,
,
,
,
,
m是方程的一个根,
,
当时,,
当时,,
若m是方程的一个根,则一定有成立,故④正确;
故答案为:①②④.
【点睛】本题考查二次函数图象和性质,解决本题关键是运用二次函数图像上点的坐标特征、抛物线与x轴交点进行计算.
27.(23-24九年级·江西上饶·期末)如图,已知抛物线与x轴交于A、B两点,与y轴交于点C,顶点为D,其中点B坐标为(3,0),顶点D的横坐标为1,轴,垂足为E,下列结论:①当时,y随x增大而减小;②;③;④;⑤当时,.其中结论正确的有 .(填序号)(多填错填倒扣一分)
【答案】③④⑤
【分析】①根据抛物线开口向下,对称轴为直线x=1,判定当x<1时,y随x增大而增大;②根据a<0,, 得到b=-2a,代入a+b=a-2a=-a>0;③x=3时,y=9a+3b+c=0,b=-2a,得到9a+3b+c=9a-6a+c=3a+c=0,根据,a<0,得到b>0,推出3a+b+c>0;④根据3a+c=0,得到c=-3a,推出 ;⑤根据抛物线与x轴交于A、B两点,其中点B坐标为(3,0),对称轴为直线x=1,得到A(-1,0)设抛物线解析式为,推出当时,-3a>2.
【详解】①当时,y随x增大而减小,
∵抛物线顶点D的横坐标为1,
∴对称轴为直线x=1,
∵抛物线开口向下,
∴当时,y随x增大而增大,
∴不正确;
②,
∵,a<0,
∴b=-2a>0,
∴a+b=a-2a=-a>0,
∴不正确;
③,
∵x=3时,y=9a+3b+c=0,b=-2a,
∴9a+3b+c=9a-6a+c=3a+c=0,
∵b>0,
∴3a+b+c>0,
∴正确;
④,
∵b=-2a,3a+c=0,
∴c=-3a,
,
∴正确;
⑤当时,,
∵抛物线与x轴交于A、B两点,其中点B坐标为(3,0),对称轴为直线x=1,
∴A(-1,0)
∴设抛物线解析式为,
当时,-3a>2,
∴正确.
故答案为,③④⑤.
【点睛】本题考查了二次函数图象与系数的关系,解决此类问题的关键是熟练掌握图象开口与a的关系,图象与y轴交点与c的关系,对称轴与a、b的关系,图象与x轴的交点特征.
28.(23-24九年级·重庆·期末)如图,函数的图象过点和,下列判断:
①;
②;
③;
④和处的函数值相等.
其中正确的是 (只填序号).
【答案】①③④
【分析】根据抛物线开口方向,对称轴以及与轴的交点即可判断①;根据、的符号得出,即可得到,根据时,得到,即可得到,即可判断②;根据抛物线与一元二次方程的关系即可判断③;根据抛物线的对称性即可判断④.
【详解】解:抛物线开口向下,
,
抛物线交轴于正半轴,
,
,
,
,故①正确,
,,
,
,
时,,则,
,
,故②错误,
的图象过点和,
方程的根为,,
方程的根为,
,
,故③正确;
的图象过点和,
抛物线的对称轴为直线,
,
和处的函数值相等,故④正确,
故答案为:①③④.
【点睛】本题考查了二次函数图象与系数的关系:对于二次函数,二次项系数决定抛物线的开口方向:当时,抛物线向上开口;当时,抛物线向下开口;一次项系数和二次项系数共同决定对称轴的位置:当与同号时(即,对称轴在轴左;当与异号时(即,对称轴在轴右;常数项决定抛物线与轴交点:抛物线与轴交于;△决定抛物线与轴交点个数:△时,抛物线与轴有2个交点;△时,抛物线与轴有1个交点;△时,抛物线与轴没有交点.
29.(23-24九年级·广东广州·期末)抛物线y=ax2+bx+c中,b=4a,它的图象如图,有以下结论:①c>0;②a+b+c>0;③a﹣b+c>0 ④b2﹣4ac<0;⑤abc<0;⑥4a>c;其中正确的为 (填序号).
【答案】①②⑥.
【分析】由抛物线的开口向上可知a>0,与y轴的交点为在y轴的正半轴上可得c>0,由此判定①正确;由4a-b和对称轴为x=- =-2,则a、b同号,即b>0,然后即可判定⑤错误;由抛物线与x轴有两个交点得到b2-4ac>0,由此判定④错误;当x=1时,y=a+b+c>0,由此判定②正确;当x=-1时,y=a-b+c<0,由此判定③错误;由a-b+c<0,而2a=b,可以推出c
【详解】解:∵抛物线的开口向上,
∴a>0,
∵与y轴的交点为在y轴的正半轴上,
∴c>0,
∴①正确;
∵对称轴为x==﹣1,得2a=b,
∴a、b同号,即b>0,
∴abc>0,
∴⑤错误;
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴④错误;
当x=1时,y=a+b+C>0,
∴②正确;
当x=﹣1时,y=a﹣b+c<0,
∴③错误;
∵a﹣b+c<0,4a=b,
∴c<3a,
∴4a>c,
∴⑥正确.
故填空答案:①②⑥.
【点睛】本题考查了二次函数的图象与系数的关系,二次函数y=ax2+bx+c系数符号的确定以及灵活运用数形结合思想是解答本题的关键.
30.(23-24九年级·湖北武汉·阶段练习)已知二次函数的图象过点,,,且交轴的正半轴于点,下列结论: ; ;若直线与抛物线只有一个公共点,则;抛物线上的两点,,在的左边,若,则; ,请将所有正确的序号填在横线上 .
【答案】
【分析】本题考查了二次函数图象与系数的关系及二次函数的性质,抛物线与 轴的交点,抛物线的对称性等知识点,根据二次函数的图象进行逐项分析即可,灵活运用有关知识来分析是解题的关键.
【详解】∵图象过点,,,
∴抛物线对称轴为直线,,
∴与轴交于点,即有,故正确;
∵交轴的正半轴于点,
∴抛物线开口向下,
∴,,,则,故正确;
由抛物线对称轴为直线,
∴,则,
∴代入得:,
∴抛物线,直线与抛物线只有一个公共点,
∴,整理得:
∴,解得:,
∴直线,代入得:,
∴,故正确;
∵抛物线上的两点,,
∴,,
∴,
∵,,,
即,
∴,故错误;
∵,
∴错误,
∴正确;
故答案为:.
21世纪教育网(www.21cnjy.com)
同课章节目录
