苏教版六年级数学上学期第一单元培优B卷(无答案)
文档属性
| 名称 | 苏教版六年级数学上学期第一单元培优B卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 130.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-12 11:08:02 | ||
图片预览



文档简介
苏教版六年级上学期第一单元培优B卷
一、填空题
1、单位换算问题
2.1m =________dm ; 3.8L=________L________ml
4300cm =________dm ; 360ml=________L
9dm =________L; 8600cm =________dm
0.8dm =________cm =________mm ; 4.07m =________m ________dm
9.08dm =________L=________ml 0.08m =________L= ________ml
10.2L=________L________ml=________cm 9600cm =________dm =________L
9.1m =________m ________dm =________dm .
2、填上适当的单位
一间教室的占地面积48________. 一枝铅笔长大约15________.
火柴盒的体积大约是20________. 一瓶英雄牌墨水的容积大约20________.
小明每步的长度约是60________ 学校操场的占地面积大约是1000________.
一桶纯净水的体积是50________. 一节火车车厢的容积大约是40________.
小明身高是1.52________. 十枚一元硬币的体积是1.9________.
3、正方体是由________个完全相同的________围成的立体图形, 正方体有________条棱, 正方体有________个顶点。因为正方体是长、宽、高都________的长方体, 所以正方体是________的长方体。
4、正方体表面积是72dm , 占地面积是________dm ; 一根长96cm的铁丝围成一个正方体, 这个正方体的棱长是________cm, 这个正方体的体积是________dm ; 一个正方体的底面积是25dm , 它的表面积是________dm , 它的体积是________dm 。
5、相交于一个顶点的________条棱, 分别叫做长方体的________、________、________; 一个长方体的体积是90cm , 长6cm, 宽5cm, 高________cm, 表面积是________cm , 锯成最大的正方体, 最多可以锯成________个, 把它锯成棱长是3cm的小正方体, 可以锯成________个。
6、至少要________个小正方体才能拼成一个大正方体, 如果一个小正方体的棱长是5cm, 那么大正方体的表面积是________cm , 体积是________cm 。
变试题:如图是一个由棱长1cm的小正方体堆成的模型.
(1)这个模型的体积是________cm ; (2)它的占地面积是________cm ;
(3)从左面看到的图形的面积是________cm ; (4)照这样堆成5层, 需要________个小正方体.
(5)立体图形是由________个小正方体搭成的.至少还需要________个同样大小的小正方体, 才能搭成一个大正方体.
7、把三个棱长都是4cm的正方体拼成一个长方体, 它的表面积是________cm , 表面积减少了________cm , 它的体积是________cm ; 一个长方体正好分割成3个体积相等的立方体, 已知一个立方体的表面积是3cm , 原来长方体的表面积是________cm 。
8、一个棱长是5dm的正方体水池, 蓄水的水面低于池口2dm, 水的容量是________L.
挖一个长和宽都是5m的长方体菜窖, 要使菜窖的容积是50m , 应该挖________深.
9、用一根52cm长的铅丝, 正好可以焊成长6cm, 宽4cm, 高________cm的长方体教具, 用纸片把这个框架包起来, 需要纸片________cm 。
10、如果把长方体的长、宽、高都扩大3倍, 那么它的体积扩大________倍, 表面积扩大________倍, 棱长和扩大________倍。
11、一个正方体的棱长为A, 棱长之和是________, 棱长是4dm的正方体, 棱长总和是________dm, 表面积是________dm , 体积是________dm 。
12、一个长方体的长是1m4dm, 宽是5dm, 高是5 dm, 这个长方体有________个面是正方形, 每个面的面积是________dm ; 其余四个面是长方形的面积大小________, 每个面的面积是________dm ; 这个长方体的表面积是________dm , 体积是________dm 。
13、用几个体积是1cm 的正方体木块摆成一个物体, 从正面、侧面和上面看到的形状如图.这个物体的体积是________cm , 表面积是________cm .
变试题:用几个1cm 的正方体木块摆了一个物体.下面是从不同方向看到的图形.这个物体的体积是________cm .
14、一个正方体的棱长总和是72cm, 它的一个面是边长________cm的正方形, 它的表面积是________cm , 体积是________cm 。
15、至少需要________cm长的铁丝, 才能做一个底面周长是18cm, 高3cm的长方体框架。
16、一个长方体的棱长总和是48cm, 底面周长是18cm, 高是________cm; 一个长方体的棱长之和是104cm, 长7cm, 宽9cm, 高是________cm, 它的表面积是________cm , 体积是________cm 。
17、一个底面是正方形的长方体, 它的侧面展开后正好是一个边长为4dm的正方形, 这个长方体的体积是________dm , 表面积是________cm 。
18、一个长方体的纸盒长是10cm, 宽是8cm, 高是4cm, 最大的面的长是________cm, 宽是________cm,面积是________cm ; 最小的面的面积是________cm .这个长方体的体积是________cm ; 三个这样的长方体拼成一个大长方体, 长方体的表面积最大是________cm , 最小是________cm 。
19、一个长方体相交于一个顶点的三条棱分别长5cm、3cm、4cm, 这个长方体的所有棱长之和是________cm。体积是________
20、一张长方形铁皮, 四角剪去边长2cm的正方形, 宽剩下6cm, 做成一只容积为192cm 的无盖铁盒子, 原来这张铁皮的长是________cm, 做这只铁盒子至少需要铁皮________cm 。
21、一个立方体和一个长方体拼在一起成了一个新的长方体, 新长方体比原来长方体的表面积增加60cm , 这个立方体的表面积是________cm ; 从一根长方体木料上截下一段体积48dm 的长方体木块剩下的部分正好是一个棱长4dm的立方体木块, 原来这根木料的表面积是________dm 。
22、有一个立方体, 如果它的高增加3cm成为长方体, 这个长方体的表面积就比原来的立方体增加96cm , 原来这个立方体的体积是________cm 。
23、一只长方体水箱, 长1dm, 宽4.5cm, 水中浸没一只钢球, 水深为8.2cm, 如果把钢球从水中取出, 水面就下降0.2cm, 这只钢球重________克(1cm 钢重7.8克); 再往水箱里放入一石块, 这时水面离箱底14cm, 问石块的体积至少是________cm 。
24、如图是一个长3m、宽与高都是2m的长方体.将它挖掉一个棱长1m的小正方体后, 它的表面积是________m .
24题图 25题图 26题图 27题图
25、如图, 用64个小正方体拼成一个大正方体, 把它的表面全部涂成红色.
(1)没有涂到颜色的小正方体有________块. (2)一面涂色的小正方体有________块.
(3)两面涂色的小正方体有________块. (4)三面涂色的小正方体有________块.
变试题一:.把一个长9cm, 宽8cm, 高6cm的长方体表面全部涂上绿色, 然后把它切成棱长为1cm的小正方体.在这些小正方体中, 只有一面涂色的有________块, 只有两面涂色的有________块.
变试题二: 一个正方体, 表面涂上颜色, 切成125个棱长1cm的小正方体, 一面涂色的小正方体有________个; 两面涂色的小正方体有________个; 三面涂色的小正方体有________个; 没有涂色的小正方体有________个。
变式题三:将一块长为 5 dm、宽为 6dm、高为 1m的长方体木料,所有的面涂成红色,锯成棱长
是1dm的小正方体,三面涂色的有________个。
26、如图, 一个正方体的六个面分别编写号1, 2, 3, 4, 5, 6, 根据图中提供的三种摆放情况.请你判断:1和________相对, 2和________相对, 三个正方体朝左那一面的数字之和是________.
变试题:所示的是一个正方体包装盒的表面展开图, 各个面上标注的数字分别为1, 2, 3, 4, 5, 6。现将表面展开图复原为正方体包装盒, 则标注数字1和3的两个面是互相平行的, 请你写出另一组相互平行的面上所对应的数字:________。
27、如图的立体图形是用边长为1cm的小正方体积木叠成的.这个立体图形的表面积是________cm , 体积是________cm .
28、把棱长是1dm的正方体切成棱长是1cm的小正方体, 然后将这些小正方体拼成一个宽和高都是1cm的长方体, 这个长方体长是________cm, 体积是________cm , 表面积是________cm ; 如果把这些小正方体紧挨着排成一行, 长________m.
29、一个长方体长是1.6dm, 宽是0.4dm, 高是0.5dm.
(1)它最小面的面积是________.
(2)可以切成棱长0.2dm的正方体________个.
(3)如果用一根铁丝围这个长方体框架需要________m铁丝.
(4)如果用它切一个最大的正方体, 其棱长是________.围这个正方体的框架需要铁丝________m.
(5)如果它切成两个长方体, 表面积最大可以增加________cm , 最少可以增加________cm .
30、新定义运算:
规定“△”满足:8△3=8+9+10=27, 7△4=7+8+9+10=34, 6△5=6+7+8+9+10=40, 求1△10=________.
规定A*B=3A+4B, 已知7*x=45, 求x=________.
规定:A※B=(A+B)+A÷B, 请计算出:8※4=如果A※4=84, 则A= .
规定a*b=5×a﹣×b(其中a, b是自然数), 那么10*6=________, 6*10=________
二、选择题
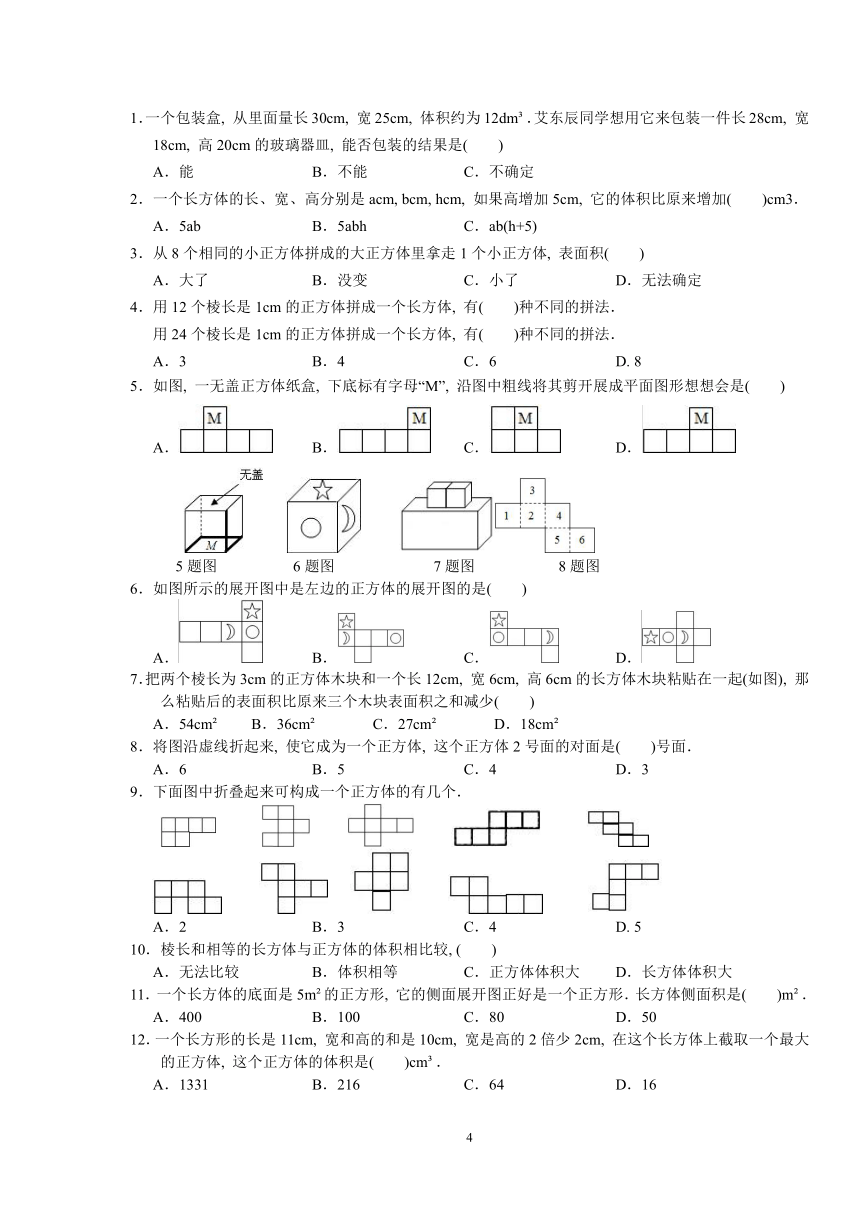
1.一个包装盒, 从里面量长30cm, 宽25cm, 体积约为12dm .艾东辰同学想用它来包装一件长28cm, 宽18cm, 高20cm的玻璃器皿, 能否包装的结果是( )
A.能 B.不能 C.不确定
2.一个长方体的长、宽、高分别是acm, bcm, hcm, 如果高增加5cm, 它的体积比原来增加( )cm3.
A.5ab B.5abh C.ab(h+5)
3.从8个相同的小正方体拼成的大正方体里拿走1个小正方体, 表面积( )
A.大了 B.没变 C.小了 D.无法确定
4.用12个棱长是1cm的正方体拼成一个长方体, 有( )种不同的拼法.
用24个棱长是1cm的正方体拼成一个长方体, 有( )种不同的拼法.
A.3 B.4 C.6 D. 8
5.如图, 一无盖正方体纸盒, 下底标有字母“M”, 沿图中粗线将其剪开展成平面图形想想会是( )
A. B. C. D.
5题图 6题图 7题图 8题图
6.如图所示的展开图中是左边的正方体的展开图的是( )
A. B. C. D.
7.把两个棱长为3cm的正方体木块和一个长12cm, 宽6cm, 高6cm的长方体木块粘贴在一起(如图), 那么粘贴后的表面积比原来三个木块表面积之和减少( )
A.54cm B.36cm C.27cm D.18cm
8.将图沿虚线折起来, 使它成为一个正方体, 这个正方体2号面的对面是( )号面.
A.6 B.5 C.4 D.3
9.下面图中折叠起来可构成一个正方体的有几个.
A.2 B.3 C.4 D. 5
10.棱长和相等的长方体与正方体的体积相比较, ( )
A.无法比较 B.体积相等 C.正方体体积大 D.长方体体积大
11.一个长方体的底面是5m 的正方形, 它的侧面展开图正好是一个正方形.长方体侧面积是( )m .
A.400 B.100 C.80 D.50
12.一个长方形的长是11cm, 宽和高的和是10cm, 宽是高的2倍少2cm, 在这个长方体上截取一个最大的正方体, 这个正方体的体积是( )cm .
A.1331 B.216 C.64 D.16
13.长方形的体积扩大9倍, 可能是( )
A.长方形的长、宽、高各扩大3倍. B.长方形的长扩大3倍, 宽和高不变.
C.长方形的长、宽各扩大3倍, 高缩小3倍. D.长方形的长不变, 宽和高各扩大3倍.
14.一个正方体棱长为acm, 如果它的棱长增加4cm, 所得到的正方体的体积比原正方体增加( )cm .
A.16 B.64 C.(a+3) ﹣a D.无法计算
15.下列说法中, 正确的有( )个。
(1)长方体中, 有时有两个相对的面是正方形。 (2)同一个正方体的六个面的面积都相等。
(3)长方体中有时四个面是完全一样的长方形。 (4)正方体棱长是6cm时, 表面积和体积就相等。
(5)正方体的棱长扩大3倍, 体积就扩大9倍。 (6)一瓶白酒有500L。
(7)长方体中的三条棱分别叫做长、宽、高. (8)求一个容器的容积, 就是求这个容器的体积.
(9) 体积相等的两个正方体, 表面积也一定相等。 (10) 棱长为1的无盖正方体铁箱, 表面积是5。
(11)一个长方体和一个正方体的底面周长和高都相等, 那么它们的体积也一定相等。
(12)一个长方体和一个正方体的表面积相等, 那么它们的体积也一定相等。
A. 4 B. 6 C. 7 D.8
三、计算题
(1)脱式计算(能简算的要用简便方法计算)
96.5×12.4﹣96.5×8 3.01×101﹣30.1×0.1 21.8×0.09+2.18×1.1
9×38.02+9×0.99×2 2.65×1.7+1.35×1.7﹣1.7 765×64×0.5×2.5×0.125
1+2+3+4+5+…+100 (0.125+1.25+12.5+125)×8 25×(0.32+0.32+0.32×2)
(14.7×0.4+4.3×0.4)×2.5 89.3×43+38×89.3+893×1.9 0.0495×2500+495×0.24+51×4.95
560×0.7-5.6÷0.2+56 ×3.5 9.9+99.9+999.9+9999.9+99999.9+0.5
(2)解方程.
25x﹣40×0.2=15 0.3x+1.5x=1.98 18﹣2(1.5x-5)=7
12.3x﹣7.5x=57.6 (3x﹣7)÷5=16 3(x﹣0.4)=0.18
4x﹣4×8=16 5(x+2.5)=21.5 (x﹣4)÷2=4.5
2.计算下面图形的体积和表面积.
四、解答题
1.把一个体积为1dm 的正方体切割成棱长为1cm的小正方体, 一共可以切成多少块 如果把这些小正方体摆成一排, 形成一个长方体, 这个长方体长多少m 这个长方体的表面积是多少dm
2.加工一个长方体铁皮油桶, 长2.5dm, 宽1.6dm, 高3dm, 至少要用多少dm 铁皮 如果每升汽油重0.72千克, 可装汽油多少千克
3.如图是一个横截面为正方形的长方体木料, 它的长是15dm, 沿虚线切开后表面积增加了32cm , 这根木料的体积是多少dm
4、学校举行运动会, 为造一个沙坑, 把1.6m 的黄沙铺在一个长4m、宽2m的长方体沙坑里, 铺平后沙子有多厚
5、某度假村建一个长方体游泳池, 长50m, 宽36m, 深2m.
①这个游泳池占地多少m
②在其底面和内壁抹一层水泥, 抹水泥的面是多少m
③在其内壁1.6m高处用红漆画一条水位线, 水位线全长多少m
④在安全范围内, 游泳池共可注水多少m
6、有一个完全封闭的长方体容器, 里面的长是20cm, 宽是10cm, 高是16cm.平放时水面高8cm(如图1), 如果把这个容器竖起来放(如图2), 水的高度会是多少cm
7、有一块正方形铁皮, 从四个顶点分别剪下一个边长2cm的正方形后, 所剩部分正好焊接成一个无盖的正方体铁皮盒。原来正方形铁皮的面积是多少cm
8、把一张长24cm、宽12cm的长方形铁皮, 你能把它剪成5块焊成一个底面是正方形的长方体的容器吗(不许浪费材料, 画出剪的图)
9、在一个长20m, 宽8m, 深1.5m的长方体蓄水池里面贴瓷砖, 瓷砖是边长为0.2m的正方形, 贴完共需瓷砖多少块
10、在一节长120cm, 宽和高都是10cm的通风管, 至少需要铁皮多少cm 做12节这样的通风管呢
11、一盒饼干长20cm, 宽15cm, 高30cm,在它的四周贴上商标纸, 这张商标纸的表面积是多少cm
12、一个长方体的无盖铁皮水桶, 长和宽都是2.5dm, 深6dm。做一对这样的水桶, 至少需要多少dm 铁皮
13、在一个长10m、宽3.5m的长方形客厅的地面上铺设2cm厚的木地板, 至少需要木材多少m 铺好要在地板上涂上油漆, 油漆面积是多少
14、在一个长方体蓄水池里放进一块长和宽都是5 cm的长方体铁块,如果把它全部放入水里,池里水面就上升 9cm,如果把水中的铁块露出 8 cm,这时池里的水面就下降4 cm.问:这个铁块的体积是多少cm
15、加、减、乘、除这四种运算的意义和运算法则我们都很熟悉.除了这四种运算之外, 我们还可以人为地规定一些其它运算, 并给出特定的运算规则, 这样的运算形式我们一般称之为定义新运算.它使用的是一些特殊的运算符号, 如*、△、▽、⊙等, 这与四则运算中的“+、﹣、×、÷”表示的意义是不同的, 其运算规则中运用的计算方法与我们所学的四则运算方法相同, 解题的关键是通过表达式寻找到运算规则.
如果2*3=2+3+4=9, 5*4=5+6+7+8=26, 那么:7*5=________, 8*2=________.
求:(1)1*(4*2)=________; (2)解方程:x*3=15.
16、有红、黄、白三种颜色的乒乓球,已知红、黄两种球平均11个;黄白两球平均8个;红白两球平均9个.三种球各多少个
17、某校参加六一杯小学数学竞赛,原定考场若干个。如果增加2个考场,每个考场正好坐24人;如
果减少2个考场,每个考场正好坐30人。参加这次竞赛的学生共有多少人
一、填空题
1、单位换算问题
2.1m =________dm ; 3.8L=________L________ml
4300cm =________dm ; 360ml=________L
9dm =________L; 8600cm =________dm
0.8dm =________cm =________mm ; 4.07m =________m ________dm
9.08dm =________L=________ml 0.08m =________L= ________ml
10.2L=________L________ml=________cm 9600cm =________dm =________L
9.1m =________m ________dm =________dm .
2、填上适当的单位
一间教室的占地面积48________. 一枝铅笔长大约15________.
火柴盒的体积大约是20________. 一瓶英雄牌墨水的容积大约20________.
小明每步的长度约是60________ 学校操场的占地面积大约是1000________.
一桶纯净水的体积是50________. 一节火车车厢的容积大约是40________.
小明身高是1.52________. 十枚一元硬币的体积是1.9________.
3、正方体是由________个完全相同的________围成的立体图形, 正方体有________条棱, 正方体有________个顶点。因为正方体是长、宽、高都________的长方体, 所以正方体是________的长方体。
4、正方体表面积是72dm , 占地面积是________dm ; 一根长96cm的铁丝围成一个正方体, 这个正方体的棱长是________cm, 这个正方体的体积是________dm ; 一个正方体的底面积是25dm , 它的表面积是________dm , 它的体积是________dm 。
5、相交于一个顶点的________条棱, 分别叫做长方体的________、________、________; 一个长方体的体积是90cm , 长6cm, 宽5cm, 高________cm, 表面积是________cm , 锯成最大的正方体, 最多可以锯成________个, 把它锯成棱长是3cm的小正方体, 可以锯成________个。
6、至少要________个小正方体才能拼成一个大正方体, 如果一个小正方体的棱长是5cm, 那么大正方体的表面积是________cm , 体积是________cm 。
变试题:如图是一个由棱长1cm的小正方体堆成的模型.
(1)这个模型的体积是________cm ; (2)它的占地面积是________cm ;
(3)从左面看到的图形的面积是________cm ; (4)照这样堆成5层, 需要________个小正方体.
(5)立体图形是由________个小正方体搭成的.至少还需要________个同样大小的小正方体, 才能搭成一个大正方体.
7、把三个棱长都是4cm的正方体拼成一个长方体, 它的表面积是________cm , 表面积减少了________cm , 它的体积是________cm ; 一个长方体正好分割成3个体积相等的立方体, 已知一个立方体的表面积是3cm , 原来长方体的表面积是________cm 。
8、一个棱长是5dm的正方体水池, 蓄水的水面低于池口2dm, 水的容量是________L.
挖一个长和宽都是5m的长方体菜窖, 要使菜窖的容积是50m , 应该挖________深.
9、用一根52cm长的铅丝, 正好可以焊成长6cm, 宽4cm, 高________cm的长方体教具, 用纸片把这个框架包起来, 需要纸片________cm 。
10、如果把长方体的长、宽、高都扩大3倍, 那么它的体积扩大________倍, 表面积扩大________倍, 棱长和扩大________倍。
11、一个正方体的棱长为A, 棱长之和是________, 棱长是4dm的正方体, 棱长总和是________dm, 表面积是________dm , 体积是________dm 。
12、一个长方体的长是1m4dm, 宽是5dm, 高是5 dm, 这个长方体有________个面是正方形, 每个面的面积是________dm ; 其余四个面是长方形的面积大小________, 每个面的面积是________dm ; 这个长方体的表面积是________dm , 体积是________dm 。
13、用几个体积是1cm 的正方体木块摆成一个物体, 从正面、侧面和上面看到的形状如图.这个物体的体积是________cm , 表面积是________cm .
变试题:用几个1cm 的正方体木块摆了一个物体.下面是从不同方向看到的图形.这个物体的体积是________cm .
14、一个正方体的棱长总和是72cm, 它的一个面是边长________cm的正方形, 它的表面积是________cm , 体积是________cm 。
15、至少需要________cm长的铁丝, 才能做一个底面周长是18cm, 高3cm的长方体框架。
16、一个长方体的棱长总和是48cm, 底面周长是18cm, 高是________cm; 一个长方体的棱长之和是104cm, 长7cm, 宽9cm, 高是________cm, 它的表面积是________cm , 体积是________cm 。
17、一个底面是正方形的长方体, 它的侧面展开后正好是一个边长为4dm的正方形, 这个长方体的体积是________dm , 表面积是________cm 。
18、一个长方体的纸盒长是10cm, 宽是8cm, 高是4cm, 最大的面的长是________cm, 宽是________cm,面积是________cm ; 最小的面的面积是________cm .这个长方体的体积是________cm ; 三个这样的长方体拼成一个大长方体, 长方体的表面积最大是________cm , 最小是________cm 。
19、一个长方体相交于一个顶点的三条棱分别长5cm、3cm、4cm, 这个长方体的所有棱长之和是________cm。体积是________
20、一张长方形铁皮, 四角剪去边长2cm的正方形, 宽剩下6cm, 做成一只容积为192cm 的无盖铁盒子, 原来这张铁皮的长是________cm, 做这只铁盒子至少需要铁皮________cm 。
21、一个立方体和一个长方体拼在一起成了一个新的长方体, 新长方体比原来长方体的表面积增加60cm , 这个立方体的表面积是________cm ; 从一根长方体木料上截下一段体积48dm 的长方体木块剩下的部分正好是一个棱长4dm的立方体木块, 原来这根木料的表面积是________dm 。
22、有一个立方体, 如果它的高增加3cm成为长方体, 这个长方体的表面积就比原来的立方体增加96cm , 原来这个立方体的体积是________cm 。
23、一只长方体水箱, 长1dm, 宽4.5cm, 水中浸没一只钢球, 水深为8.2cm, 如果把钢球从水中取出, 水面就下降0.2cm, 这只钢球重________克(1cm 钢重7.8克); 再往水箱里放入一石块, 这时水面离箱底14cm, 问石块的体积至少是________cm 。
24、如图是一个长3m、宽与高都是2m的长方体.将它挖掉一个棱长1m的小正方体后, 它的表面积是________m .
24题图 25题图 26题图 27题图
25、如图, 用64个小正方体拼成一个大正方体, 把它的表面全部涂成红色.
(1)没有涂到颜色的小正方体有________块. (2)一面涂色的小正方体有________块.
(3)两面涂色的小正方体有________块. (4)三面涂色的小正方体有________块.
变试题一:.把一个长9cm, 宽8cm, 高6cm的长方体表面全部涂上绿色, 然后把它切成棱长为1cm的小正方体.在这些小正方体中, 只有一面涂色的有________块, 只有两面涂色的有________块.
变试题二: 一个正方体, 表面涂上颜色, 切成125个棱长1cm的小正方体, 一面涂色的小正方体有________个; 两面涂色的小正方体有________个; 三面涂色的小正方体有________个; 没有涂色的小正方体有________个。
变式题三:将一块长为 5 dm、宽为 6dm、高为 1m的长方体木料,所有的面涂成红色,锯成棱长
是1dm的小正方体,三面涂色的有________个。
26、如图, 一个正方体的六个面分别编写号1, 2, 3, 4, 5, 6, 根据图中提供的三种摆放情况.请你判断:1和________相对, 2和________相对, 三个正方体朝左那一面的数字之和是________.
变试题:所示的是一个正方体包装盒的表面展开图, 各个面上标注的数字分别为1, 2, 3, 4, 5, 6。现将表面展开图复原为正方体包装盒, 则标注数字1和3的两个面是互相平行的, 请你写出另一组相互平行的面上所对应的数字:________。
27、如图的立体图形是用边长为1cm的小正方体积木叠成的.这个立体图形的表面积是________cm , 体积是________cm .
28、把棱长是1dm的正方体切成棱长是1cm的小正方体, 然后将这些小正方体拼成一个宽和高都是1cm的长方体, 这个长方体长是________cm, 体积是________cm , 表面积是________cm ; 如果把这些小正方体紧挨着排成一行, 长________m.
29、一个长方体长是1.6dm, 宽是0.4dm, 高是0.5dm.
(1)它最小面的面积是________.
(2)可以切成棱长0.2dm的正方体________个.
(3)如果用一根铁丝围这个长方体框架需要________m铁丝.
(4)如果用它切一个最大的正方体, 其棱长是________.围这个正方体的框架需要铁丝________m.
(5)如果它切成两个长方体, 表面积最大可以增加________cm , 最少可以增加________cm .
30、新定义运算:
规定“△”满足:8△3=8+9+10=27, 7△4=7+8+9+10=34, 6△5=6+7+8+9+10=40, 求1△10=________.
规定A*B=3A+4B, 已知7*x=45, 求x=________.
规定:A※B=(A+B)+A÷B, 请计算出:8※4=如果A※4=84, 则A= .
规定a*b=5×a﹣×b(其中a, b是自然数), 那么10*6=________, 6*10=________
二、选择题
1.一个包装盒, 从里面量长30cm, 宽25cm, 体积约为12dm .艾东辰同学想用它来包装一件长28cm, 宽18cm, 高20cm的玻璃器皿, 能否包装的结果是( )
A.能 B.不能 C.不确定
2.一个长方体的长、宽、高分别是acm, bcm, hcm, 如果高增加5cm, 它的体积比原来增加( )cm3.
A.5ab B.5abh C.ab(h+5)
3.从8个相同的小正方体拼成的大正方体里拿走1个小正方体, 表面积( )
A.大了 B.没变 C.小了 D.无法确定
4.用12个棱长是1cm的正方体拼成一个长方体, 有( )种不同的拼法.
用24个棱长是1cm的正方体拼成一个长方体, 有( )种不同的拼法.
A.3 B.4 C.6 D. 8
5.如图, 一无盖正方体纸盒, 下底标有字母“M”, 沿图中粗线将其剪开展成平面图形想想会是( )
A. B. C. D.
5题图 6题图 7题图 8题图
6.如图所示的展开图中是左边的正方体的展开图的是( )
A. B. C. D.
7.把两个棱长为3cm的正方体木块和一个长12cm, 宽6cm, 高6cm的长方体木块粘贴在一起(如图), 那么粘贴后的表面积比原来三个木块表面积之和减少( )
A.54cm B.36cm C.27cm D.18cm
8.将图沿虚线折起来, 使它成为一个正方体, 这个正方体2号面的对面是( )号面.
A.6 B.5 C.4 D.3
9.下面图中折叠起来可构成一个正方体的有几个.
A.2 B.3 C.4 D. 5
10.棱长和相等的长方体与正方体的体积相比较, ( )
A.无法比较 B.体积相等 C.正方体体积大 D.长方体体积大
11.一个长方体的底面是5m 的正方形, 它的侧面展开图正好是一个正方形.长方体侧面积是( )m .
A.400 B.100 C.80 D.50
12.一个长方形的长是11cm, 宽和高的和是10cm, 宽是高的2倍少2cm, 在这个长方体上截取一个最大的正方体, 这个正方体的体积是( )cm .
A.1331 B.216 C.64 D.16
13.长方形的体积扩大9倍, 可能是( )
A.长方形的长、宽、高各扩大3倍. B.长方形的长扩大3倍, 宽和高不变.
C.长方形的长、宽各扩大3倍, 高缩小3倍. D.长方形的长不变, 宽和高各扩大3倍.
14.一个正方体棱长为acm, 如果它的棱长增加4cm, 所得到的正方体的体积比原正方体增加( )cm .
A.16 B.64 C.(a+3) ﹣a D.无法计算
15.下列说法中, 正确的有( )个。
(1)长方体中, 有时有两个相对的面是正方形。 (2)同一个正方体的六个面的面积都相等。
(3)长方体中有时四个面是完全一样的长方形。 (4)正方体棱长是6cm时, 表面积和体积就相等。
(5)正方体的棱长扩大3倍, 体积就扩大9倍。 (6)一瓶白酒有500L。
(7)长方体中的三条棱分别叫做长、宽、高. (8)求一个容器的容积, 就是求这个容器的体积.
(9) 体积相等的两个正方体, 表面积也一定相等。 (10) 棱长为1的无盖正方体铁箱, 表面积是5。
(11)一个长方体和一个正方体的底面周长和高都相等, 那么它们的体积也一定相等。
(12)一个长方体和一个正方体的表面积相等, 那么它们的体积也一定相等。
A. 4 B. 6 C. 7 D.8
三、计算题
(1)脱式计算(能简算的要用简便方法计算)
96.5×12.4﹣96.5×8 3.01×101﹣30.1×0.1 21.8×0.09+2.18×1.1
9×38.02+9×0.99×2 2.65×1.7+1.35×1.7﹣1.7 765×64×0.5×2.5×0.125
1+2+3+4+5+…+100 (0.125+1.25+12.5+125)×8 25×(0.32+0.32+0.32×2)
(14.7×0.4+4.3×0.4)×2.5 89.3×43+38×89.3+893×1.9 0.0495×2500+495×0.24+51×4.95
560×0.7-5.6÷0.2+56 ×3.5 9.9+99.9+999.9+9999.9+99999.9+0.5
(2)解方程.
25x﹣40×0.2=15 0.3x+1.5x=1.98 18﹣2(1.5x-5)=7
12.3x﹣7.5x=57.6 (3x﹣7)÷5=16 3(x﹣0.4)=0.18
4x﹣4×8=16 5(x+2.5)=21.5 (x﹣4)÷2=4.5
2.计算下面图形的体积和表面积.
四、解答题
1.把一个体积为1dm 的正方体切割成棱长为1cm的小正方体, 一共可以切成多少块 如果把这些小正方体摆成一排, 形成一个长方体, 这个长方体长多少m 这个长方体的表面积是多少dm
2.加工一个长方体铁皮油桶, 长2.5dm, 宽1.6dm, 高3dm, 至少要用多少dm 铁皮 如果每升汽油重0.72千克, 可装汽油多少千克
3.如图是一个横截面为正方形的长方体木料, 它的长是15dm, 沿虚线切开后表面积增加了32cm , 这根木料的体积是多少dm
4、学校举行运动会, 为造一个沙坑, 把1.6m 的黄沙铺在一个长4m、宽2m的长方体沙坑里, 铺平后沙子有多厚
5、某度假村建一个长方体游泳池, 长50m, 宽36m, 深2m.
①这个游泳池占地多少m
②在其底面和内壁抹一层水泥, 抹水泥的面是多少m
③在其内壁1.6m高处用红漆画一条水位线, 水位线全长多少m
④在安全范围内, 游泳池共可注水多少m
6、有一个完全封闭的长方体容器, 里面的长是20cm, 宽是10cm, 高是16cm.平放时水面高8cm(如图1), 如果把这个容器竖起来放(如图2), 水的高度会是多少cm
7、有一块正方形铁皮, 从四个顶点分别剪下一个边长2cm的正方形后, 所剩部分正好焊接成一个无盖的正方体铁皮盒。原来正方形铁皮的面积是多少cm
8、把一张长24cm、宽12cm的长方形铁皮, 你能把它剪成5块焊成一个底面是正方形的长方体的容器吗(不许浪费材料, 画出剪的图)
9、在一个长20m, 宽8m, 深1.5m的长方体蓄水池里面贴瓷砖, 瓷砖是边长为0.2m的正方形, 贴完共需瓷砖多少块
10、在一节长120cm, 宽和高都是10cm的通风管, 至少需要铁皮多少cm 做12节这样的通风管呢
11、一盒饼干长20cm, 宽15cm, 高30cm,在它的四周贴上商标纸, 这张商标纸的表面积是多少cm
12、一个长方体的无盖铁皮水桶, 长和宽都是2.5dm, 深6dm。做一对这样的水桶, 至少需要多少dm 铁皮
13、在一个长10m、宽3.5m的长方形客厅的地面上铺设2cm厚的木地板, 至少需要木材多少m 铺好要在地板上涂上油漆, 油漆面积是多少
14、在一个长方体蓄水池里放进一块长和宽都是5 cm的长方体铁块,如果把它全部放入水里,池里水面就上升 9cm,如果把水中的铁块露出 8 cm,这时池里的水面就下降4 cm.问:这个铁块的体积是多少cm
15、加、减、乘、除这四种运算的意义和运算法则我们都很熟悉.除了这四种运算之外, 我们还可以人为地规定一些其它运算, 并给出特定的运算规则, 这样的运算形式我们一般称之为定义新运算.它使用的是一些特殊的运算符号, 如*、△、▽、⊙等, 这与四则运算中的“+、﹣、×、÷”表示的意义是不同的, 其运算规则中运用的计算方法与我们所学的四则运算方法相同, 解题的关键是通过表达式寻找到运算规则.
如果2*3=2+3+4=9, 5*4=5+6+7+8=26, 那么:7*5=________, 8*2=________.
求:(1)1*(4*2)=________; (2)解方程:x*3=15.
16、有红、黄、白三种颜色的乒乓球,已知红、黄两种球平均11个;黄白两球平均8个;红白两球平均9个.三种球各多少个
17、某校参加六一杯小学数学竞赛,原定考场若干个。如果增加2个考场,每个考场正好坐24人;如
果减少2个考场,每个考场正好坐30人。参加这次竞赛的学生共有多少人
