初中数学人教版八年级 第十二章 全等三角形 单元练习(无答案)
文档属性
| 名称 | 初中数学人教版八年级 第十二章 全等三角形 单元练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 323.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-12 00:00:00 | ||
图片预览



文档简介
初中数学人教版八年级全等三角形
一、单选题
1.下列选项中表示两个图形全等的是( )
A.形状相同的两个图形 B.周长相等的两个图形
C.面积相等的两个图形 D.能够完全重合的两个图形
2.如图所示,的度数是( )
A.44° B.55° C.66° D.77°
3.如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测得BC=5cm,BF=7cm,则EC长为( )
A.2cm B.3cm C.4cm D.5cm
4.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,DE⊥AC,垂足为点E,若BD=2,则DE的长为( )
A.3 B. C.2 D.6
5.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
A.65° B.55° C.45° D.35°
6.在△ABC中,AC=6,中线AD=5,则边AB的取值范围是( )
A.1<AB<11 B.4<AB<13 C.4<AB<16 D.11<AB<16
7.如图所示,在△ABC中,点O是∠BCA与∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,则点O到边BC的距离OD是( )
A.1 B.2 C.3 D.4
8.如图,在 格的正方形网格中,与△ABC有一条公共边且全等(不与△ABC重合)的格点三角形(顶点在格点上的三角形)共有( )
A.5个 B.6 个 C.7个 D.8 个
9.如图,在和中,,连接交于点,连接.下列结论:①;②;③平分;④平分.其中正确的个数为( ).
A.4 B.3 C.2 D.1
10.如图,在中,,平分交于点D,平分交于点E,,交于点F.则下列说法正确的有( )
①;②;③若,则;④.
A.1个 B.2个 C.3个 D.4个
二、填空题
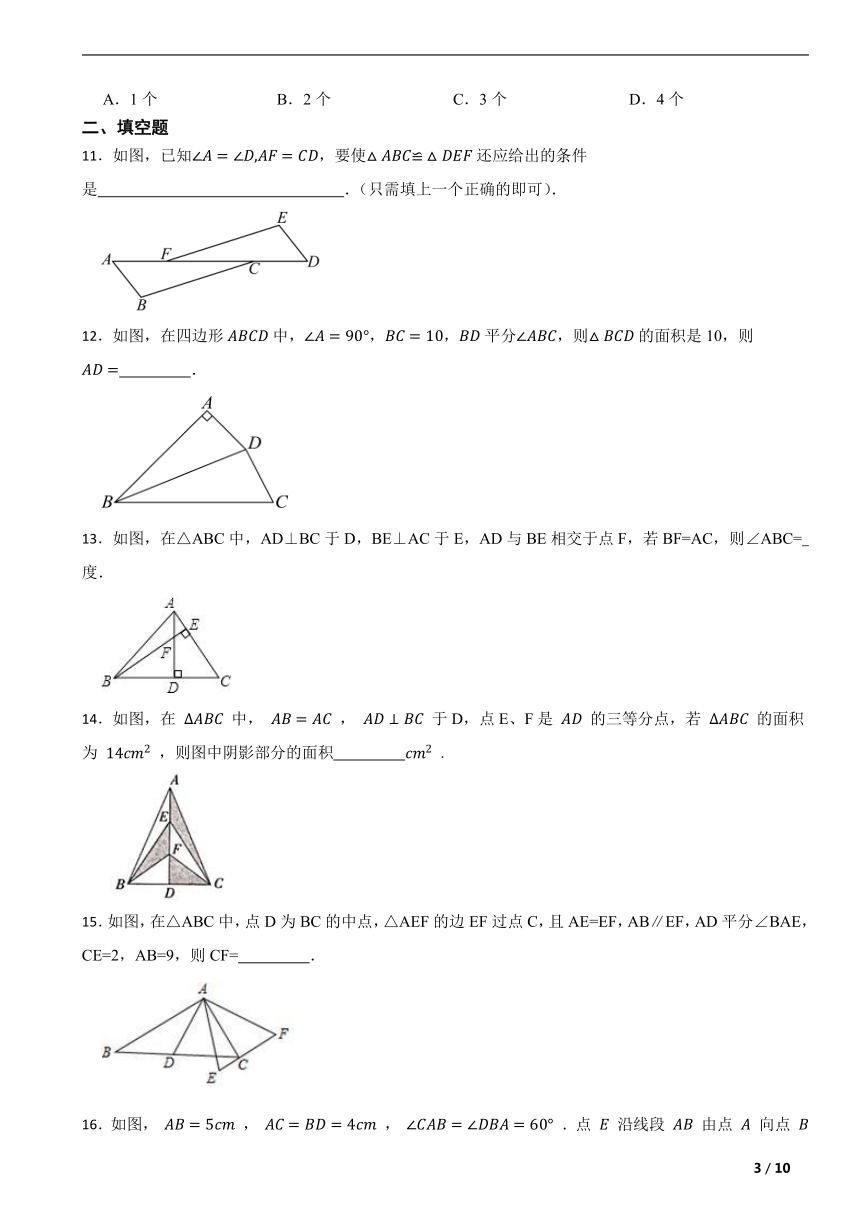
11.如图,已知,要使还应给出的条件是 .(只需填上一个正确的即可).
12.如图,在四边形中,,,平分,则的面积是10,则 .
13.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC= 度.
14.如图,在 中, , 于D,点E、F是 的三等分点,若 的面积为 ,则图中阴影部分的面积 .
15.如图,在△ABC中,点D为BC的中点,△AEF的边EF过点C,且AE=EF,AB∥EF,AD平分∠BAE,CE=2,AB=9,则CF= .
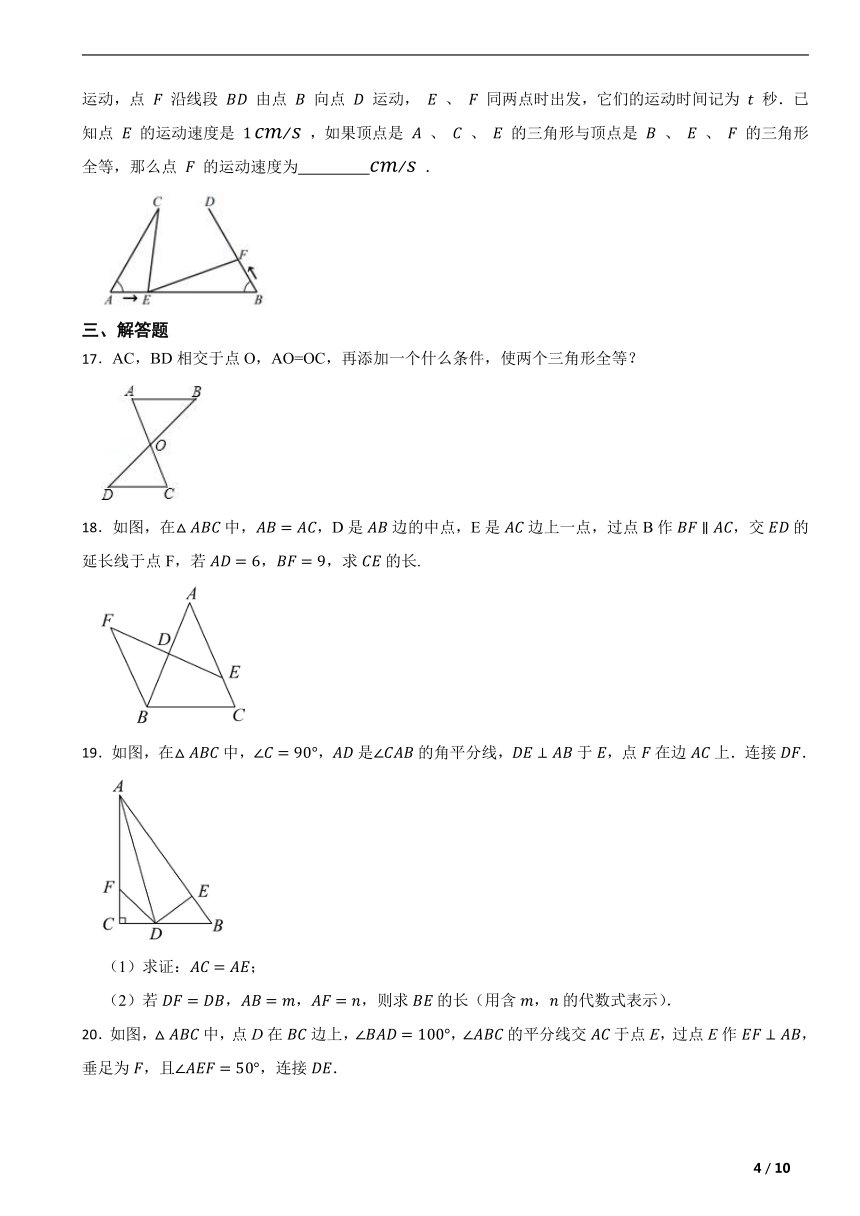
16.如图, , , .点 沿线段 由点 向点 运动,点 沿线段 由点 向点 运动, 、 同两点时出发,它们的运动时间记为 秒.已知点 的运动速度是 ,如果顶点是 、 、 的三角形与顶点是 、 、 的三角形全等,那么点 的运动速度为 .
三、解答题
17.AC,BD相交于点O,AO=OC,再添加一个什么条件,使两个三角形全等?
18.如图,在中,,D是边的中点,E是边上一点,过点B作,交的延长线于点F,若,,求的长.
19.如图,在中,,是的角平分线,于,点在边上.连接.
(1)求证:;
(2)若,,,则求的长(用含,的代数式表示).
20.如图,中,点D在边上,,的平分线交于点E,过点E作,垂足为,且,连接.
(1)求证:平分;
(2)若,求的面积.
21. 在△ABC中,AB<AC,AD为△ABC的角平分线,点E是BC边的中点.过点E作AD延长线的垂线,垂足为点G,交AC于点F,交AB的延长线于点H.
(1)求证:∠AHF=∠AFH;
(2)探究:在线段EH上是否能找到一点P,使得△BEP≌△CEF.如果能够,请找出并证明之;
(3)证明:BH=CF.
22.请阅读下列材料:
问题:在四边形ABCD中,M是BC边的中点,且∠AMD=90°
(1)如图1,若AB与CD不平行,试判断AB+CD与AD之间的数量关系;
小雪同学的思路是:延长DM至E使DM=ME,连接AE,BE,构造全等三角形,经过推理使问题得到解决请你参考小雪的思路,在图1中把图形补充完整,并直接写出上面问题AB+CD与AD之间的数量关系:
(2)如图2,若在原条件的基础上,增加AM平分∠BAD,(1)中结论还成立吗?若不成立,写出AB+CD与AD之间的数量关系,并证明.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】B
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】C
11.【答案】(答案不唯一)
12.【答案】2
13.【答案】45
14.【答案】7
15.【答案】5
16.【答案】1或
17.【答案】解:∵OA=OC,OB=OD,∠AOB=∠COD(对顶角相等),
∴△ABO≌△CDO(SAS);
∵OA=OC,∠A=∠C,∠AOB=∠COD(对顶角相等),
∴△ABO≌△CDO(ASA);
∵OA=OC,∠B=∠D,∠AOB=∠COD(对顶角相等),
∴△ABO≌△CDO(AAS);
∵AB∥DC,
∴∠A=∠C,
∵OA=OC,∠A=∠C,∠AOB=∠COD(对顶角相等),
∴△ABO≌△CDO(ASA).
故答案为BO=DO或∠A=∠C或∠B=∠D或AB∥DC.
18.【答案】解:∵
∴,
∵D为的中点,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴.
19.【答案】(1)证明:∵,,
∴,
∵是的角平分线,
∴,
在和中,
,
∴,
∴;
(2)解:由(1)可知,
∴,
在和中,
,
∴,
∴,
由(1)可知,
∵,
∴,
∵,
∴,
∵,,
∴.
20.【答案】(1)证明:如图,过点E作于G,于H,
∵,
∴,
∵,
∴,
∴,
∴为的平分线,
又,
∴,
∵是的平分线,
∴,
∴,
∴点E在的平分线上,
∴平分;
(2)解:设,则,
∴,即:,
解得,,
∴,
∴的面积为.
21.【答案】(1)证明:∵AD为△ABC的角平分线,
∴∠HAG=∠FAG,
∵FH⊥AD,
∴∠AGH=∠AGF=90°,
在△AHG和△AFG中,
,
∴△AHG≌△AFG(ASA),
∴∠AHF=∠AFH.
(2)解:在线段EH上能找到一点P,使得△BEP≌△CEF,理由如下:
作BP∥AC,交EH于点P,则△BEP≌△CEF,
证明:∵点E是BC边的中点,
∴BE=CE,
∵BP∥AC,
∴∠EBP=∠C,
在△BEP和△CEF中,
,
∴△BEP≌△CEF(ASA);
(3)证明:∵△BEP≌△CEF,
∴BP=CF,
∵BP∥AC,
∴∠BPH=∠AFH,
∵∠AHF=∠AFH,
∴∠BPH=∠AHF,
∴BH=BP,
∴BH=CF.
22.【答案】(1)解: AB与CD不平行
根据题意,延长DM使DM=EM,连接BE,AE,EC,BD
由于M是BC的中点,故BM=MC
∴四边形BECE是平行四边形
∴CD=BE
又 EM=DM,且∠AMD=90°
∴ 是等腰三角形
∴AD=AB
在 中,
(2)解:若在原条件的基础上,增加AM平分∠BAD
则(1)的结论不成立
关系为:
证明:由于M是BC的中点,故BM=MC
∴四边形BECE是平行四边形
∴CD=BE
又 EM=DM,且∠AMD=90°
∴ 是等腰三角形
∴AD=AE
又 AM平分∠BAD
∴点A.B.E必然共线
∴
1 / 1
一、单选题
1.下列选项中表示两个图形全等的是( )
A.形状相同的两个图形 B.周长相等的两个图形
C.面积相等的两个图形 D.能够完全重合的两个图形
2.如图所示,的度数是( )
A.44° B.55° C.66° D.77°
3.如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测得BC=5cm,BF=7cm,则EC长为( )
A.2cm B.3cm C.4cm D.5cm
4.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,DE⊥AC,垂足为点E,若BD=2,则DE的长为( )
A.3 B. C.2 D.6
5.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
A.65° B.55° C.45° D.35°
6.在△ABC中,AC=6,中线AD=5,则边AB的取值范围是( )
A.1<AB<11 B.4<AB<13 C.4<AB<16 D.11<AB<16
7.如图所示,在△ABC中,点O是∠BCA与∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,则点O到边BC的距离OD是( )
A.1 B.2 C.3 D.4
8.如图,在 格的正方形网格中,与△ABC有一条公共边且全等(不与△ABC重合)的格点三角形(顶点在格点上的三角形)共有( )
A.5个 B.6 个 C.7个 D.8 个
9.如图,在和中,,连接交于点,连接.下列结论:①;②;③平分;④平分.其中正确的个数为( ).
A.4 B.3 C.2 D.1
10.如图,在中,,平分交于点D,平分交于点E,,交于点F.则下列说法正确的有( )
①;②;③若,则;④.
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,已知,要使还应给出的条件是 .(只需填上一个正确的即可).
12.如图,在四边形中,,,平分,则的面积是10,则 .
13.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC= 度.
14.如图,在 中, , 于D,点E、F是 的三等分点,若 的面积为 ,则图中阴影部分的面积 .
15.如图,在△ABC中,点D为BC的中点,△AEF的边EF过点C,且AE=EF,AB∥EF,AD平分∠BAE,CE=2,AB=9,则CF= .
16.如图, , , .点 沿线段 由点 向点 运动,点 沿线段 由点 向点 运动, 、 同两点时出发,它们的运动时间记为 秒.已知点 的运动速度是 ,如果顶点是 、 、 的三角形与顶点是 、 、 的三角形全等,那么点 的运动速度为 .
三、解答题
17.AC,BD相交于点O,AO=OC,再添加一个什么条件,使两个三角形全等?
18.如图,在中,,D是边的中点,E是边上一点,过点B作,交的延长线于点F,若,,求的长.
19.如图,在中,,是的角平分线,于,点在边上.连接.
(1)求证:;
(2)若,,,则求的长(用含,的代数式表示).
20.如图,中,点D在边上,,的平分线交于点E,过点E作,垂足为,且,连接.
(1)求证:平分;
(2)若,求的面积.
21. 在△ABC中,AB<AC,AD为△ABC的角平分线,点E是BC边的中点.过点E作AD延长线的垂线,垂足为点G,交AC于点F,交AB的延长线于点H.
(1)求证:∠AHF=∠AFH;
(2)探究:在线段EH上是否能找到一点P,使得△BEP≌△CEF.如果能够,请找出并证明之;
(3)证明:BH=CF.
22.请阅读下列材料:
问题:在四边形ABCD中,M是BC边的中点,且∠AMD=90°
(1)如图1,若AB与CD不平行,试判断AB+CD与AD之间的数量关系;
小雪同学的思路是:延长DM至E使DM=ME,连接AE,BE,构造全等三角形,经过推理使问题得到解决请你参考小雪的思路,在图1中把图形补充完整,并直接写出上面问题AB+CD与AD之间的数量关系:
(2)如图2,若在原条件的基础上,增加AM平分∠BAD,(1)中结论还成立吗?若不成立,写出AB+CD与AD之间的数量关系,并证明.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】B
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】C
11.【答案】(答案不唯一)
12.【答案】2
13.【答案】45
14.【答案】7
15.【答案】5
16.【答案】1或
17.【答案】解:∵OA=OC,OB=OD,∠AOB=∠COD(对顶角相等),
∴△ABO≌△CDO(SAS);
∵OA=OC,∠A=∠C,∠AOB=∠COD(对顶角相等),
∴△ABO≌△CDO(ASA);
∵OA=OC,∠B=∠D,∠AOB=∠COD(对顶角相等),
∴△ABO≌△CDO(AAS);
∵AB∥DC,
∴∠A=∠C,
∵OA=OC,∠A=∠C,∠AOB=∠COD(对顶角相等),
∴△ABO≌△CDO(ASA).
故答案为BO=DO或∠A=∠C或∠B=∠D或AB∥DC.
18.【答案】解:∵
∴,
∵D为的中点,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴.
19.【答案】(1)证明:∵,,
∴,
∵是的角平分线,
∴,
在和中,
,
∴,
∴;
(2)解:由(1)可知,
∴,
在和中,
,
∴,
∴,
由(1)可知,
∵,
∴,
∵,
∴,
∵,,
∴.
20.【答案】(1)证明:如图,过点E作于G,于H,
∵,
∴,
∵,
∴,
∴,
∴为的平分线,
又,
∴,
∵是的平分线,
∴,
∴,
∴点E在的平分线上,
∴平分;
(2)解:设,则,
∴,即:,
解得,,
∴,
∴的面积为.
21.【答案】(1)证明:∵AD为△ABC的角平分线,
∴∠HAG=∠FAG,
∵FH⊥AD,
∴∠AGH=∠AGF=90°,
在△AHG和△AFG中,
,
∴△AHG≌△AFG(ASA),
∴∠AHF=∠AFH.
(2)解:在线段EH上能找到一点P,使得△BEP≌△CEF,理由如下:
作BP∥AC,交EH于点P,则△BEP≌△CEF,
证明:∵点E是BC边的中点,
∴BE=CE,
∵BP∥AC,
∴∠EBP=∠C,
在△BEP和△CEF中,
,
∴△BEP≌△CEF(ASA);
(3)证明:∵△BEP≌△CEF,
∴BP=CF,
∵BP∥AC,
∴∠BPH=∠AFH,
∵∠AHF=∠AFH,
∴∠BPH=∠AHF,
∴BH=BP,
∴BH=CF.
22.【答案】(1)解: AB与CD不平行
根据题意,延长DM使DM=EM,连接BE,AE,EC,BD
由于M是BC的中点,故BM=MC
∴四边形BECE是平行四边形
∴CD=BE
又 EM=DM,且∠AMD=90°
∴ 是等腰三角形
∴AD=AB
在 中,
(2)解:若在原条件的基础上,增加AM平分∠BAD
则(1)的结论不成立
关系为:
证明:由于M是BC的中点,故BM=MC
∴四边形BECE是平行四边形
∴CD=BE
又 EM=DM,且∠AMD=90°
∴ 是等腰三角形
∴AD=AE
又 AM平分∠BAD
∴点A.B.E必然共线
∴
1 / 1
