20204-2025学年北师大版九年级数学上册课件 1.1 菱形的性质与判定习题课件(第3课时)(21张PPT)
文档属性
| 名称 | 20204-2025学年北师大版九年级数学上册课件 1.1 菱形的性质与判定习题课件(第3课时)(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 517.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-12 15:07:39 | ||
图片预览




文档简介
(共21张PPT)
北师大版九年级数学上册课件
第一章 特殊平行四边形
1 菱形的性质与判定
第3课时
1.能灵活运用菱形的性质定理及判定定理解决一
些相关问题,并掌握菱形面积的求法。(重点、难点)
2.经历菱形性质定理及判定定理的应用过程,体会
数形结合、转化等思想方法。
学习目标
1.平行四边形的对边 ,对角 ,对角线 .
2.菱形具有 的一切性质.
3.菱形是 图形也是 图形.
4.菱形的四条边都 .
5.菱形的两条对角线互相 .
平行且相等
相等
互相平分
平行四边形
轴对称
中心对称
相等
垂直 且平分
复习引入
菱形的面积
一
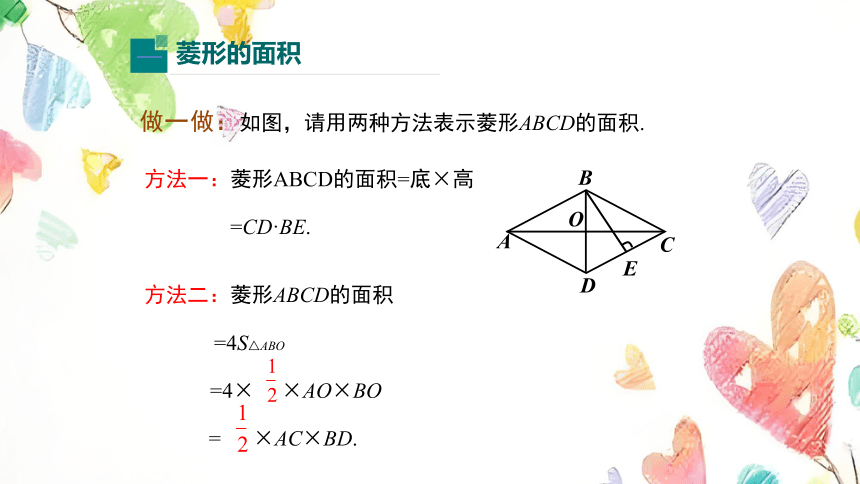
做一做:如图,请用两种方法表示菱形ABCD的面积.
方法一:菱形ABCD的面积=底×高
=CD·BE.
A
B
C
O
D
E
方法二:菱形ABCD的面积
=4S△ABO
=4× ×AO×BO
= ×AC×BD.
A
B
D
C
a
h
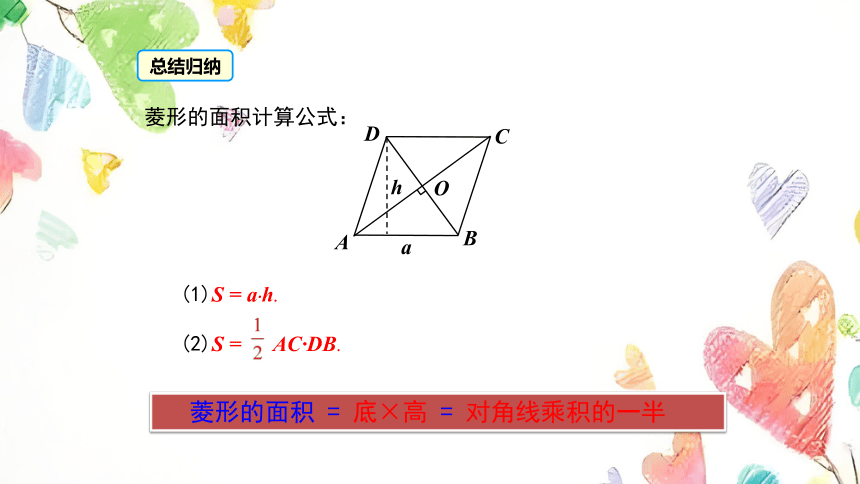
(1)S = a·h.
(2)S = AC·DB.
O
菱形的面积计算公式:
总结归纳
菱形的面积 = 底×高 = 对角线乘积的一半
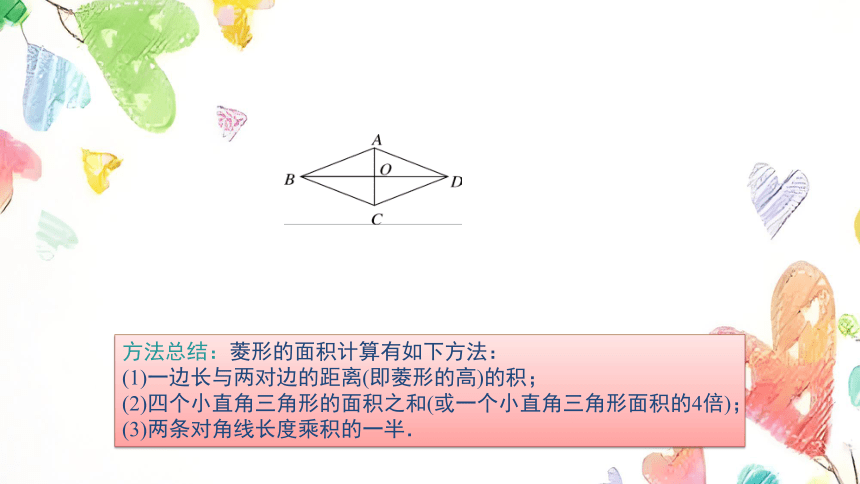
方法总结:菱形的面积计算有如下方法:
(1)一边长与两对边的距离(即菱形的高)的积;
(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍);
(3)两条对角线长度乘积的一半.
菱形的判定与性质的综合问题
二
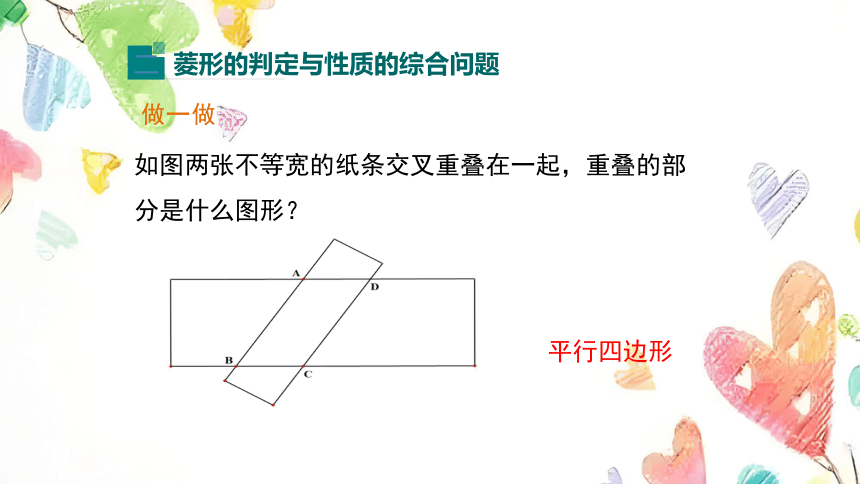
如图两张不等宽的纸条交叉重叠在一起,重叠的部分是什么图形?
做一做
平行四边形
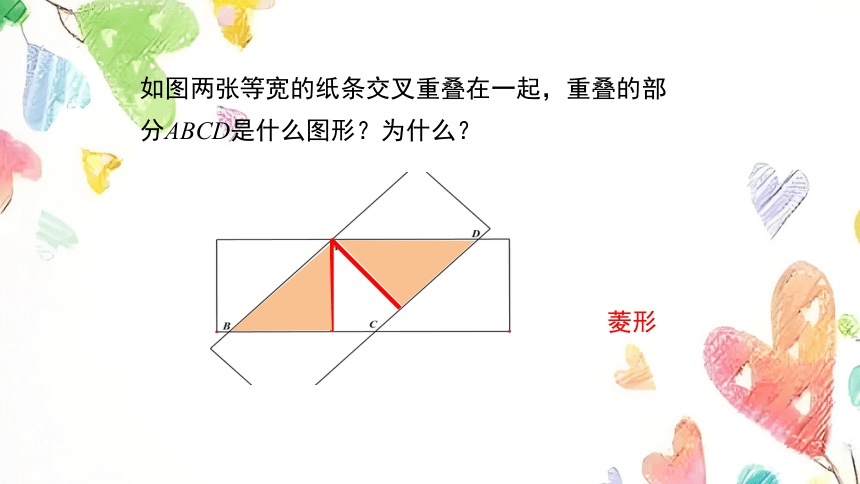
如图两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是什么图形?为什么?
菱形
方法总结:判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以尝试证出这个四边形是平行四边形,然后用定义法或判定定理1来证明菱形.
菱形的性质与判定的综合性问题
菱形的面积
有关计算
面积=底×高=两条对角线乘积的一半
若菱形的两条对角线的长分别是a,b,则菱形的面积等于 .
1. 下列关于某个四边形的三个结论:①对角线互相平分;②是一个菱形;③是一个平行四边形.下列推理过程正确的是( )
A. 由②推出③,由③推出①
B. 由①推出②,由②推出③
C. 由③推出①,由①推出②
D. 由①推出③,由③推出②
A
2. 如图,在菱形ABCD中,E,F,G,H分别是菱形四边的中
点,连接EG,FH,且EG,FH交于点O,则图中共有菱形( )
A. 4个B. 5个
C. 6个D. 7个
3. 若菱形的两条对角线长分别是16 cm和12 cm,则它的边长为 ,面积为 .
4. 如图,菱形ABCD的对角线的长分别为2和5,P是对角线
AC上任意一点(点P不与点A、C重合),且PE∥BC交AB于点
E,PF∥CD交AD于点F,则阴影部分的面积是 .
B
10 cm
96 cm2
2.5
5. 如图,在?ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,
F,且BE=DF.
(1)求证:?ABCD是菱形;
(2)若AB=5,AC=6,求?ABCD的面积.
(1)证明:∵四边形ABCD是平行四边形,∴∠B=∠D,
∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD=90°,
∵BE=DF,∴△AEB≌△AFD(SAS).
∴AB=AD,∴四边形ABCD是菱形.
(2)解:连接BD交AC于点O.
∵四边形ABCD是菱形,AC=6,∴AC⊥BD,
AO=OC=AC=×6=3,
∵AB=5,AO=3,
∴BO== =4,
∴BD=2BO=8,∴S平行四边形ABCD=×AC×BD=24.
【基础训练】
1. 如图,O既是AB的中点,又是CD的中点,并且AB⊥CD,连接AC,BC,AD,BD,则这四条线段的大小关系是( )
A. 全相等 B. 互不相等
C. 只有两条相等 D. 不能确定
A
2. 如图,将两根宽度都为1的纸条叠放在一起,如果∠DAB=45°,则四边形ABCD的面积为( )
A.1 B. C.2 D.
3. 如图,①以点A为圆心,半径为2 cm画弧,分别交∠MAN的两边AM,AN于点B,D;②以点B为圆心,AD长为半径画弧,再以点D为圆心,AB长为半径画弧,两弧交于点C;③分别连接BC,CD,AC.若∠MAN=60°,则∠ACB的大小为 .
C
30°
4. 如图,菱形ABCD的周长为12 cm,BC的垂直平分线EF经过点A,则对角线BD的长是 cm.
5. 如图所示,学校有一处花坛是由两个一样的菱形图案组成的,小颖沿其中一个的边缘走完一周用了24s,而她从A到B用相同的速度直线行走用了6s.求∠1的度数.
3
60°
【提升训练】
6. 如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B,D分别在平面直角坐标系的y轴,x轴的正半轴上滑动,连接OA,则OA的长的最小值是 .
7. 如图所示,AD∥FE,点B,C在AD上,∠1=∠2,BF=BC.
(1)求证:四边形BCEF是菱形;
(2)若AB=BC=CD,求证:△ACF≌△BDE.
5-5
证明:(1)∵AD∥FE,∴∠FEB=∠2.
∵∠1=∠2,∴∠FEB=∠1.∴EF=BF.
∵BF=BC,∴BC=EF.
又∵BC∥EF,∴四边形BCEF是平行四边形.
∵BF=BC,∴四边形BCEF是菱形.
(2)∵EF=BC,AB=BC=CD,AD∥EF,
∴四边形ABEF,CDEF均为平行四边形.
∴AF=BE,FC=ED.
∵AC=2BC=BD,∴△ACF≌△BDE(SSS).
【拓展训练】
8. 如图,在△ABC中,P是边AC上的一个动点,过点P作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:PE=PF;
(2)当点P在边AC上运动时,四边形BCFE可能是
菱形吗 请说明理由.
(1)证明:∵CE平分∠BCA,∴∠BCE=∠PCE.
∵MN∥BC,∴∠PEC=∠BCE. ∴∠PEC=∠PCE.∴PE=PC.
同理可证PC=PF.∴PE=PF.
(2)解:四边形BCFE不可能是菱形.理由如下:
若四边形BCFE为菱形,则BF⊥EC. 由(1),可得FC⊥EC.
∵在平面内过同一点F不可能有两条直线垂直于同一条直线,
∴BF⊥EC不能成立. ∴四边形BCFE不可能是菱形.
谢谢大家
北师大版九年级数学上册课件
第一章 特殊平行四边形
1 菱形的性质与判定
第3课时
1.能灵活运用菱形的性质定理及判定定理解决一
些相关问题,并掌握菱形面积的求法。(重点、难点)
2.经历菱形性质定理及判定定理的应用过程,体会
数形结合、转化等思想方法。
学习目标
1.平行四边形的对边 ,对角 ,对角线 .
2.菱形具有 的一切性质.
3.菱形是 图形也是 图形.
4.菱形的四条边都 .
5.菱形的两条对角线互相 .
平行且相等
相等
互相平分
平行四边形
轴对称
中心对称
相等
垂直 且平分
复习引入
菱形的面积
一
做一做:如图,请用两种方法表示菱形ABCD的面积.
方法一:菱形ABCD的面积=底×高
=CD·BE.
A
B
C
O
D
E
方法二:菱形ABCD的面积
=4S△ABO
=4× ×AO×BO
= ×AC×BD.
A
B
D
C
a
h
(1)S = a·h.
(2)S = AC·DB.
O
菱形的面积计算公式:
总结归纳
菱形的面积 = 底×高 = 对角线乘积的一半
方法总结:菱形的面积计算有如下方法:
(1)一边长与两对边的距离(即菱形的高)的积;
(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍);
(3)两条对角线长度乘积的一半.
菱形的判定与性质的综合问题
二
如图两张不等宽的纸条交叉重叠在一起,重叠的部分是什么图形?
做一做
平行四边形
如图两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是什么图形?为什么?
菱形
方法总结:判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以尝试证出这个四边形是平行四边形,然后用定义法或判定定理1来证明菱形.
菱形的性质与判定的综合性问题
菱形的面积
有关计算
面积=底×高=两条对角线乘积的一半
若菱形的两条对角线的长分别是a,b,则菱形的面积等于 .
1. 下列关于某个四边形的三个结论:①对角线互相平分;②是一个菱形;③是一个平行四边形.下列推理过程正确的是( )
A. 由②推出③,由③推出①
B. 由①推出②,由②推出③
C. 由③推出①,由①推出②
D. 由①推出③,由③推出②
A
2. 如图,在菱形ABCD中,E,F,G,H分别是菱形四边的中
点,连接EG,FH,且EG,FH交于点O,则图中共有菱形( )
A. 4个B. 5个
C. 6个D. 7个
3. 若菱形的两条对角线长分别是16 cm和12 cm,则它的边长为 ,面积为 .
4. 如图,菱形ABCD的对角线的长分别为2和5,P是对角线
AC上任意一点(点P不与点A、C重合),且PE∥BC交AB于点
E,PF∥CD交AD于点F,则阴影部分的面积是 .
B
10 cm
96 cm2
2.5
5. 如图,在?ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,
F,且BE=DF.
(1)求证:?ABCD是菱形;
(2)若AB=5,AC=6,求?ABCD的面积.
(1)证明:∵四边形ABCD是平行四边形,∴∠B=∠D,
∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD=90°,
∵BE=DF,∴△AEB≌△AFD(SAS).
∴AB=AD,∴四边形ABCD是菱形.
(2)解:连接BD交AC于点O.
∵四边形ABCD是菱形,AC=6,∴AC⊥BD,
AO=OC=AC=×6=3,
∵AB=5,AO=3,
∴BO== =4,
∴BD=2BO=8,∴S平行四边形ABCD=×AC×BD=24.
【基础训练】
1. 如图,O既是AB的中点,又是CD的中点,并且AB⊥CD,连接AC,BC,AD,BD,则这四条线段的大小关系是( )
A. 全相等 B. 互不相等
C. 只有两条相等 D. 不能确定
A
2. 如图,将两根宽度都为1的纸条叠放在一起,如果∠DAB=45°,则四边形ABCD的面积为( )
A.1 B. C.2 D.
3. 如图,①以点A为圆心,半径为2 cm画弧,分别交∠MAN的两边AM,AN于点B,D;②以点B为圆心,AD长为半径画弧,再以点D为圆心,AB长为半径画弧,两弧交于点C;③分别连接BC,CD,AC.若∠MAN=60°,则∠ACB的大小为 .
C
30°
4. 如图,菱形ABCD的周长为12 cm,BC的垂直平分线EF经过点A,则对角线BD的长是 cm.
5. 如图所示,学校有一处花坛是由两个一样的菱形图案组成的,小颖沿其中一个的边缘走完一周用了24s,而她从A到B用相同的速度直线行走用了6s.求∠1的度数.
3
60°
【提升训练】
6. 如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B,D分别在平面直角坐标系的y轴,x轴的正半轴上滑动,连接OA,则OA的长的最小值是 .
7. 如图所示,AD∥FE,点B,C在AD上,∠1=∠2,BF=BC.
(1)求证:四边形BCEF是菱形;
(2)若AB=BC=CD,求证:△ACF≌△BDE.
5-5
证明:(1)∵AD∥FE,∴∠FEB=∠2.
∵∠1=∠2,∴∠FEB=∠1.∴EF=BF.
∵BF=BC,∴BC=EF.
又∵BC∥EF,∴四边形BCEF是平行四边形.
∵BF=BC,∴四边形BCEF是菱形.
(2)∵EF=BC,AB=BC=CD,AD∥EF,
∴四边形ABEF,CDEF均为平行四边形.
∴AF=BE,FC=ED.
∵AC=2BC=BD,∴△ACF≌△BDE(SSS).
【拓展训练】
8. 如图,在△ABC中,P是边AC上的一个动点,过点P作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:PE=PF;
(2)当点P在边AC上运动时,四边形BCFE可能是
菱形吗 请说明理由.
(1)证明:∵CE平分∠BCA,∴∠BCE=∠PCE.
∵MN∥BC,∴∠PEC=∠BCE. ∴∠PEC=∠PCE.∴PE=PC.
同理可证PC=PF.∴PE=PF.
(2)解:四边形BCFE不可能是菱形.理由如下:
若四边形BCFE为菱形,则BF⊥EC. 由(1),可得FC⊥EC.
∵在平面内过同一点F不可能有两条直线垂直于同一条直线,
∴BF⊥EC不能成立. ∴四边形BCFE不可能是菱形.
谢谢大家
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
