2024年江苏省淮安市中考数学试题(PDF版,无答案)
文档属性
| 名称 | 2024年江苏省淮安市中考数学试题(PDF版,无答案) | 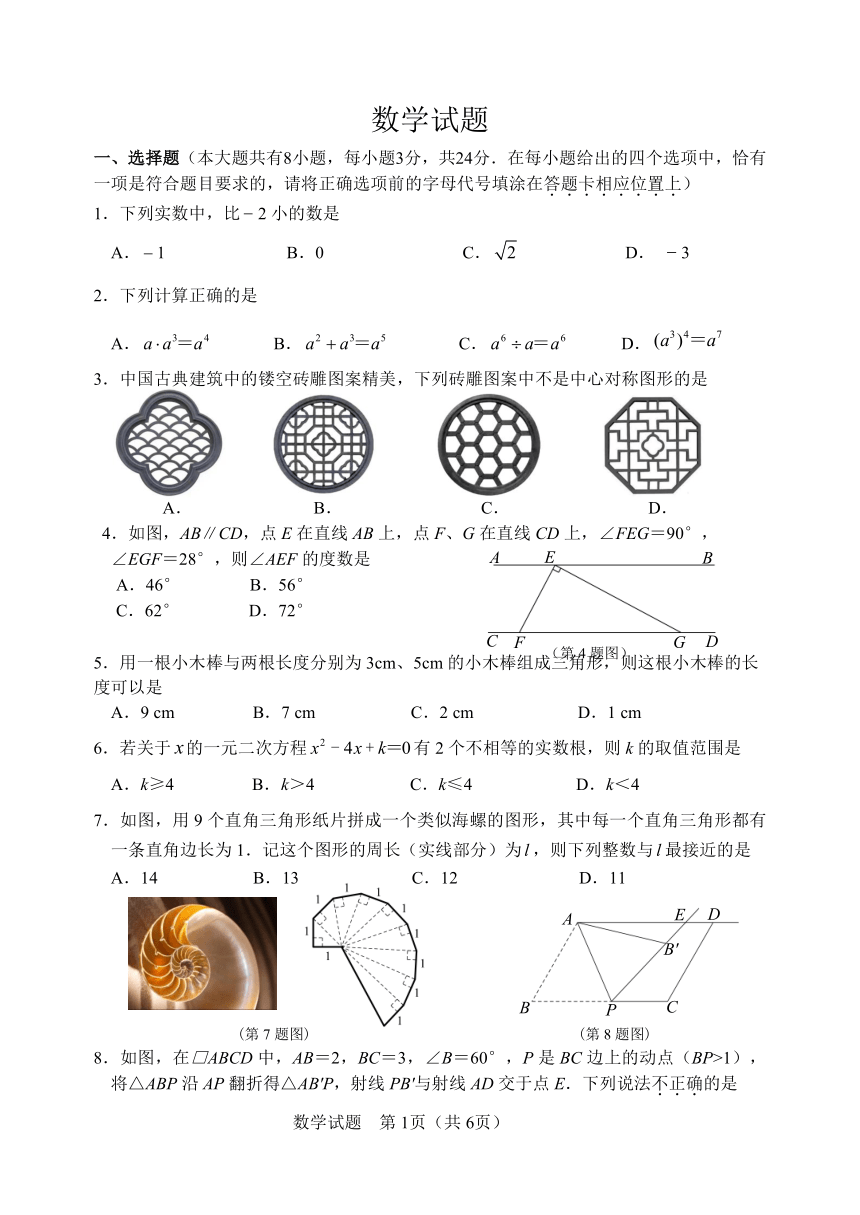 | |
| 格式 | |||
| 文件大小 | 680.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-12 15:52:39 | ||
图片预览



文档简介
数学试题
一、选择题(本大题共有8小题,每小题3分,共24分.在每小题给出的四个选项中,恰有
一项是符合题目要求的,请将正确选项前的字母代号填涂在答.题.卡.相.应.位.置.上.)
1.下列实数中,比 2小的数是
A. 1 B.0 C. 2 D. 3
2.下列计算正确的是
A. a a3=a4 B. a2 a3 3 4 7=a5 C. a6 a=a6 D. (a ) =a
3.中国古典建筑中的镂空砖雕图案精美,下列砖雕图案中不是中心对称图形的是
A. B. C. D.
4.如图,AB∥CD,点 E在直线 AB上,点 F、G在直线 CD上,∠FEG=90°,
∠EGF=28°,则∠AEF的度数是 A E B
A.46° B.56°
C.62° D.72°
C F G D
5.用一根小木棒与两根长度分别为 3cm、5cm (第 4题图)的小木棒组成三角形,则这根小木棒的长
度可以是
A.9 cm B.7 cm C.2 cm D.1 cm
6.若关于 x的一元二次方程 x2 - 4x + k=0有 2个不相等的实数根,则 k的取值范围是
A.k≥4 B.k>4 C.k≤4 D.k<4
7.如图,用 9个直角三角形纸片拼成一个类似海螺的图形,其中每一个直角三角形都有
一条直角边长为 1.记这个图形的周长(实线部分)为 l,则下列整数与 l最接近的是
A.14 B.13 C.12 D.11
A E D
B'
B P C
(第 7题图) (第 8题图)
8.如图,在□ABCD中,AB=2,BC=3,∠B=60°,P是 BC边上的动点(BP>1),
将△ABP沿 AP翻折得△AB'P,射线 PB'与射线 AD交于点 E.下列说法不.正.确.的是
数学试题 第 1页(共 6页)
{#{QQABQYwy1U4owgAgwgAgNIJYAACBTh5CbQQw0n2ooCAQAsQkBIGERAJCUYgguOAhUECAKIIOAAwAQiABJFABIAAA==}#}#}}
A.当 AB'⊥AB时,B'A=B'E
B.当点 B'落在 AD上时,四边形 ABPB'是菱形
C.在点 P运动的过程中,线段 AE的最小值为 2
D.连接 BB' 1,则四边形 ABPB'的面积始终等于 AP BB
2
第Ⅱ卷(非选择题共 126分)
二、填空题(本大题共有8小题,每小题3分,共24分.不需写出解答过程,请把答案直接
写在答.题.卡.相.应.位.置.上.)
9 1.计算: 8 = ▲ .
2
10.分解因式: a2 16= ▲ .
11.2024年 5月 3日嫦娥六号成功发射,它将在相距约 380000km的地月之间完成月壤样品
的“空中接力”.数据 380000用科学记数法表示为 ▲ .
12.一只不透明的袋中装有8个白球和若干个红球,这些球除颜色外都相同, A
搅匀后每次随机从袋中摸出一个球,记下颜色后放回袋中.通过大量重复摸
O
球试验后发现,摸到白球的频率是0.4,则袋中约有红球 ▲ 个.
13.如图, △ABC是⊙O的内接三角形,∠BAC=50°,⊙O半径为 3,则 B C
B C (第 13题图)的长为 ▲ .
14.一辆轿车从 A地驶向 B地,设出发 xh后,这辆轿车离 B地路程为 ykm,已知 y与 x
之间的函数表达式为 y=200–80x,则轿车从 A地到达 B地所用时间是 ▲ h.
15.某公园广场的地面由形状、大小完全相同的一种地砖密铺(无空隙、不重叠的拼接)而
成,铺设方式如图 1.图 2是其中一块地砖的示意图,AB=EF,CD=GH,BC=FG,BC∥FG,
AB∥CD∥GH∥EF,部分尺寸如图所示(单位:dm).结合图 1、图 2信息,可求得 BC的
长度是 ▲ dm. F E E D
3 Q
H C D 7 F C
3
G B
A 10 A P B
图 1 图 2
(第 15题图) (第 16题图)
16.如图,点 P是正六边形 ABCDEF的边 AB的中点,一束光线从点 P出发,照射到镜面
EF上的点 Q处,经反射后恰好经过顶点 C.已知正六边形的边长为 2,则 EQ= ▲ .
(第 8 题图)
三、解答题(本大题共有 11小题,共 102分.请在答.题.卡.指.定.区.域.内.作.答.,解答时应写
数学试题 第 2页(共 6页)
{#{QQABQYwy1U4owgAgwgAgNIJYAACBTh5CbQQw0n2ooCAQAsQkBIGERAJCUYgguOAhUECAKIIOAAwAQiABJFABIAAA==}#}#}}
出必要的文字说明、证明过程或演算步骤)
17.(本小题满分 10分)
(1)计算: tan 60 1 0 3 ;
(2 x x - 3)解不等式: ≥ + 2.
2 3
18 3 x 1.(本小题满分 8分)先化简,再求值: 1 2 ,其中 x= 3. x 2 x 4x 4
19.(本小题满分 8分)已知:如图,在矩形 ABCD中,点 E、F在 BD上,BE=DF.
求证:△ABE≌△CDF. A D
F
E
B C
(第 19 题图)
20.(本小题满分 8分)《张丘建算经》由北魏数学家张丘建所著,其中有这样一个问题:
“今有客不知其数.两人共盘,少两盘;三人共盘,长三盘.问客及盘各几何?”意思为:
“现有若干名客人.若 2个人共用 1个盘子,则少 2个盘子;若 3个人共用 1个盘子,则
多出来 3个盘子.问客人和盘子各有多少?”请你解答这个问题.
21.(本小题满分 8分)历史文化名城淮安有着丰富的旅游资源.小明计划假期来淮安游玩,
他打算从 3个人文景点(A.周恩来纪念馆;B.吴承恩故居;C.河下古镇)中随机选取一个,
再从 2个自然景点(D.金湖水上森林;E.铁山寺国家森林公园)中随机选取一个.
(1)小明从人文景点中选中河下古镇的概率是 ▲ ;
(2)用树状图或列表的方法求小明恰好选中周恩来纪念馆和铁山寺国家森林公园的概率.
22.(本小题满分 8分)张老师早上开车到学校上班有两条路线,路线一经城市高架,路
线二经市区道路.为了解上班路上所用时间,张老师记录了 20 个工作日的上班路上用时
其中 10个工作日走路线一,另外 10个工作日走路线二.根据记录数据绘制成如下统计图:
数学试题 第 3页(共 6页)
{#{QQABQYyw1U4owgAgwgAgNIJYAACBTh5CbQQw0n2ooCAQAsQkBIGERAJCUYgguOAhUECAKIIOAAwAQiABJFABIAAA==}#}#}}
时间/分钟
序号
(1)根据以上数据把表格补充完整:
平均数 中位数 众数 方差 极差
路线一 ▲ 18 ▲ 2.4 5
路线二 15.6 ▲ 11 18.04 ▲
(2)请你帮助张老师选择其中一种上班路线,并利用以上至少 2个统计量说明理由.
23.(本小题满分 8分)拉杆箱是外出旅行常用工具.某种拉杆箱示意图如下图所示(滚
轮忽略不计),箱体截面是矩形 BCDE,BC的长度为 60cm,两节可调节的拉杆长度相
等,且与 BC 在同一条直线上.如图 1,当拉杆伸出一节(AB)时,AC与地面夹角∠ACG
=53°;如图 2,当拉杆伸出两节(AM、MB)时,AC与地面夹角∠ACG=37°,两种
情况下拉杆把手 A点距离地面高度相同.求每节拉杆的长度.
(参考数据: sin53 4
3 4 3
, sin37 , tan53 , tan37 )
5 5 3 4
A
E A E
B M
B
D
D
G C G C
图 1 (第 23题图) 图 2
数学试题 第 4页(共 6页)
{#{QQABQYwy1U4owgAgwgAgNIJYAACBTh5CbQQw0n2ooCAQAsQkBIGERAJCUYgguOAhUECAKIIOAAwAQiABJFABIAAA==}#}#}}
24.(本小题满分 8分)如图,在平面直角坐标系中,一次函数 y=k1x +b的图像与 x轴、
y轴分别交于点 A、B,与反比例函数 y k= 2 (x 0)的图像交于点 C.已知点 A坐标为(–1,0),
x
点 C坐标为(1,3).
(1)求反比例函数及一次函数的表达式;
(2)点 D在线段 OB上,过点 D且平行于 x轴的直线交 AB于点 E,交反比例函数图像于
点 F.当 DO=2ED时,求点 F的坐标.
y
C
B
E D F
A O x
(第 24题图)
25.(本小题满分 10分)如图,在△ABC中,BA=BC,以 AB为直径作⊙O交 AC于点 D,
过点 D作 DE⊥BC,垂足为 E,延长 DE交 AB的延长线于点 F.
(1)求证:DF为⊙O的切线; F
(2)若 BE=1, BF=3,求 sinC的值.
B
E
O
A D C
(第 25题图)
26.(本小题满分 12分)二次函数 y ax2 bx c的图像经过点 A(0,8),顶点为 P.
(1)c= ▲ ;
1
(2)当 a= 时,
4
①若顶点 P到 x轴的距离为 10,则 b= ▲ ;
②直线 m过点(0,2b)且垂直于 y轴,顶点 P到直线 m的距离为 h.随着 b的增大,
h的值如何变化?请描述变化过程,并说明理由;
(3)若二次函数图像交 x轴于B、C两点,点B坐标为(8,0),且△ABC的面积不小于 20,
求 a的取值范围.
数学试题 第 5页(共 6页)
{#{QQABQYwy1U4owgAgwgAgNIJYAACBTh5CbQQw0n2ooCAQAsQkBIGERAJCUYgguOAhUECAKIIOAAwAQiABJFABIAAA==}#}#}}
27.(本小题满分 14分)综合与实践
【问题初探】(1)某兴趣小组探索这样一个问题:若 AD是△ABC的角平分线,则线段
AB、AC、BD、CD有何数量关系?下面是小智、小勇的部分思路和方法,请完成填空:
小智的思路和方法: 小勇的思路和方法:
如图 1,作 DM⊥AB,DN⊥AC,垂足分 如图 2,作 CE∥AB,交 AD的延长线于
别为 M、N. 点 E. A
∵AD平分∠BAC,DM⊥AB,DN⊥AC, ∵AD平分∠BAC,
∴ ▲ . A ∴∠BAD=∠CAD.
1 ∵CE∥AB,
∵ S ABD= AB DM,
B D C
2 ∴∠BAD=∠E.
M
1 N ∴∠CAD=∠E.S ACD= AC DN, E2 ∴ ▲ . 图 2
S ABD AB
B D C
∴ . 再通过证明△CDE∽△BDA得到比例式,=
S AC 图 1 ACD 从而推导出结论……
再用另一种方式表示△ABD与△ACD的
面积,即可推导出结论……
根据小智或小勇的方法,可以得到线段 AB、AC、BD、CD的数量关系是 ▲ .
【变式拓展】(2)小慧对问题作了进一步拓展:如图 3,在△ABC中,AB=AC,D是 BC
边上一点,∠BAD=45°,∠CAD=60°,求 BD的值.请你完成解答.
CD A
A
D E
B D C E F B C
图 3 图 4 图 5
【迁移应用】(3)请你借助以上结论或方法,用无刻度直尺和圆规在图 4的线段 EF上作
一点 P,使 EP 3FP.(要求:不写作法,保留作图痕迹)
【综合提升】(4)如图 5,在△ABC中,AB=5,AC=4, BAC= ( <90°),点 D
在 AC边上,CD=1,点 E在 BD的延长线上,连接 EC, BEC= ( < ),请直接写出
BD DE的值(用含 , 的式子表示).
数学试题 第 6页(共 6页)
{#{QQABQYwy1U4owgAgwgAgNIJYAACBTh5CbQQw0n2ooCAQAsQkBIGERAJCUYgguOAhUECAKIIOAAwAQiABJFABIAAA==}#}#}}
一、选择题(本大题共有8小题,每小题3分,共24分.在每小题给出的四个选项中,恰有
一项是符合题目要求的,请将正确选项前的字母代号填涂在答.题.卡.相.应.位.置.上.)
1.下列实数中,比 2小的数是
A. 1 B.0 C. 2 D. 3
2.下列计算正确的是
A. a a3=a4 B. a2 a3 3 4 7=a5 C. a6 a=a6 D. (a ) =a
3.中国古典建筑中的镂空砖雕图案精美,下列砖雕图案中不是中心对称图形的是
A. B. C. D.
4.如图,AB∥CD,点 E在直线 AB上,点 F、G在直线 CD上,∠FEG=90°,
∠EGF=28°,则∠AEF的度数是 A E B
A.46° B.56°
C.62° D.72°
C F G D
5.用一根小木棒与两根长度分别为 3cm、5cm (第 4题图)的小木棒组成三角形,则这根小木棒的长
度可以是
A.9 cm B.7 cm C.2 cm D.1 cm
6.若关于 x的一元二次方程 x2 - 4x + k=0有 2个不相等的实数根,则 k的取值范围是
A.k≥4 B.k>4 C.k≤4 D.k<4
7.如图,用 9个直角三角形纸片拼成一个类似海螺的图形,其中每一个直角三角形都有
一条直角边长为 1.记这个图形的周长(实线部分)为 l,则下列整数与 l最接近的是
A.14 B.13 C.12 D.11
A E D
B'
B P C
(第 7题图) (第 8题图)
8.如图,在□ABCD中,AB=2,BC=3,∠B=60°,P是 BC边上的动点(BP>1),
将△ABP沿 AP翻折得△AB'P,射线 PB'与射线 AD交于点 E.下列说法不.正.确.的是
数学试题 第 1页(共 6页)
{#{QQABQYwy1U4owgAgwgAgNIJYAACBTh5CbQQw0n2ooCAQAsQkBIGERAJCUYgguOAhUECAKIIOAAwAQiABJFABIAAA==}#}#}}
A.当 AB'⊥AB时,B'A=B'E
B.当点 B'落在 AD上时,四边形 ABPB'是菱形
C.在点 P运动的过程中,线段 AE的最小值为 2
D.连接 BB' 1,则四边形 ABPB'的面积始终等于 AP BB
2
第Ⅱ卷(非选择题共 126分)
二、填空题(本大题共有8小题,每小题3分,共24分.不需写出解答过程,请把答案直接
写在答.题.卡.相.应.位.置.上.)
9 1.计算: 8 = ▲ .
2
10.分解因式: a2 16= ▲ .
11.2024年 5月 3日嫦娥六号成功发射,它将在相距约 380000km的地月之间完成月壤样品
的“空中接力”.数据 380000用科学记数法表示为 ▲ .
12.一只不透明的袋中装有8个白球和若干个红球,这些球除颜色外都相同, A
搅匀后每次随机从袋中摸出一个球,记下颜色后放回袋中.通过大量重复摸
O
球试验后发现,摸到白球的频率是0.4,则袋中约有红球 ▲ 个.
13.如图, △ABC是⊙O的内接三角形,∠BAC=50°,⊙O半径为 3,则 B C
B C (第 13题图)的长为 ▲ .
14.一辆轿车从 A地驶向 B地,设出发 xh后,这辆轿车离 B地路程为 ykm,已知 y与 x
之间的函数表达式为 y=200–80x,则轿车从 A地到达 B地所用时间是 ▲ h.
15.某公园广场的地面由形状、大小完全相同的一种地砖密铺(无空隙、不重叠的拼接)而
成,铺设方式如图 1.图 2是其中一块地砖的示意图,AB=EF,CD=GH,BC=FG,BC∥FG,
AB∥CD∥GH∥EF,部分尺寸如图所示(单位:dm).结合图 1、图 2信息,可求得 BC的
长度是 ▲ dm. F E E D
3 Q
H C D 7 F C
3
G B
A 10 A P B
图 1 图 2
(第 15题图) (第 16题图)
16.如图,点 P是正六边形 ABCDEF的边 AB的中点,一束光线从点 P出发,照射到镜面
EF上的点 Q处,经反射后恰好经过顶点 C.已知正六边形的边长为 2,则 EQ= ▲ .
(第 8 题图)
三、解答题(本大题共有 11小题,共 102分.请在答.题.卡.指.定.区.域.内.作.答.,解答时应写
数学试题 第 2页(共 6页)
{#{QQABQYwy1U4owgAgwgAgNIJYAACBTh5CbQQw0n2ooCAQAsQkBIGERAJCUYgguOAhUECAKIIOAAwAQiABJFABIAAA==}#}#}}
出必要的文字说明、证明过程或演算步骤)
17.(本小题满分 10分)
(1)计算: tan 60 1 0 3 ;
(2 x x - 3)解不等式: ≥ + 2.
2 3
18 3 x 1.(本小题满分 8分)先化简,再求值: 1 2 ,其中 x= 3. x 2 x 4x 4
19.(本小题满分 8分)已知:如图,在矩形 ABCD中,点 E、F在 BD上,BE=DF.
求证:△ABE≌△CDF. A D
F
E
B C
(第 19 题图)
20.(本小题满分 8分)《张丘建算经》由北魏数学家张丘建所著,其中有这样一个问题:
“今有客不知其数.两人共盘,少两盘;三人共盘,长三盘.问客及盘各几何?”意思为:
“现有若干名客人.若 2个人共用 1个盘子,则少 2个盘子;若 3个人共用 1个盘子,则
多出来 3个盘子.问客人和盘子各有多少?”请你解答这个问题.
21.(本小题满分 8分)历史文化名城淮安有着丰富的旅游资源.小明计划假期来淮安游玩,
他打算从 3个人文景点(A.周恩来纪念馆;B.吴承恩故居;C.河下古镇)中随机选取一个,
再从 2个自然景点(D.金湖水上森林;E.铁山寺国家森林公园)中随机选取一个.
(1)小明从人文景点中选中河下古镇的概率是 ▲ ;
(2)用树状图或列表的方法求小明恰好选中周恩来纪念馆和铁山寺国家森林公园的概率.
22.(本小题满分 8分)张老师早上开车到学校上班有两条路线,路线一经城市高架,路
线二经市区道路.为了解上班路上所用时间,张老师记录了 20 个工作日的上班路上用时
其中 10个工作日走路线一,另外 10个工作日走路线二.根据记录数据绘制成如下统计图:
数学试题 第 3页(共 6页)
{#{QQABQYyw1U4owgAgwgAgNIJYAACBTh5CbQQw0n2ooCAQAsQkBIGERAJCUYgguOAhUECAKIIOAAwAQiABJFABIAAA==}#}#}}
时间/分钟
序号
(1)根据以上数据把表格补充完整:
平均数 中位数 众数 方差 极差
路线一 ▲ 18 ▲ 2.4 5
路线二 15.6 ▲ 11 18.04 ▲
(2)请你帮助张老师选择其中一种上班路线,并利用以上至少 2个统计量说明理由.
23.(本小题满分 8分)拉杆箱是外出旅行常用工具.某种拉杆箱示意图如下图所示(滚
轮忽略不计),箱体截面是矩形 BCDE,BC的长度为 60cm,两节可调节的拉杆长度相
等,且与 BC 在同一条直线上.如图 1,当拉杆伸出一节(AB)时,AC与地面夹角∠ACG
=53°;如图 2,当拉杆伸出两节(AM、MB)时,AC与地面夹角∠ACG=37°,两种
情况下拉杆把手 A点距离地面高度相同.求每节拉杆的长度.
(参考数据: sin53 4
3 4 3
, sin37 , tan53 , tan37 )
5 5 3 4
A
E A E
B M
B
D
D
G C G C
图 1 (第 23题图) 图 2
数学试题 第 4页(共 6页)
{#{QQABQYwy1U4owgAgwgAgNIJYAACBTh5CbQQw0n2ooCAQAsQkBIGERAJCUYgguOAhUECAKIIOAAwAQiABJFABIAAA==}#}#}}
24.(本小题满分 8分)如图,在平面直角坐标系中,一次函数 y=k1x +b的图像与 x轴、
y轴分别交于点 A、B,与反比例函数 y k= 2 (x 0)的图像交于点 C.已知点 A坐标为(–1,0),
x
点 C坐标为(1,3).
(1)求反比例函数及一次函数的表达式;
(2)点 D在线段 OB上,过点 D且平行于 x轴的直线交 AB于点 E,交反比例函数图像于
点 F.当 DO=2ED时,求点 F的坐标.
y
C
B
E D F
A O x
(第 24题图)
25.(本小题满分 10分)如图,在△ABC中,BA=BC,以 AB为直径作⊙O交 AC于点 D,
过点 D作 DE⊥BC,垂足为 E,延长 DE交 AB的延长线于点 F.
(1)求证:DF为⊙O的切线; F
(2)若 BE=1, BF=3,求 sinC的值.
B
E
O
A D C
(第 25题图)
26.(本小题满分 12分)二次函数 y ax2 bx c的图像经过点 A(0,8),顶点为 P.
(1)c= ▲ ;
1
(2)当 a= 时,
4
①若顶点 P到 x轴的距离为 10,则 b= ▲ ;
②直线 m过点(0,2b)且垂直于 y轴,顶点 P到直线 m的距离为 h.随着 b的增大,
h的值如何变化?请描述变化过程,并说明理由;
(3)若二次函数图像交 x轴于B、C两点,点B坐标为(8,0),且△ABC的面积不小于 20,
求 a的取值范围.
数学试题 第 5页(共 6页)
{#{QQABQYwy1U4owgAgwgAgNIJYAACBTh5CbQQw0n2ooCAQAsQkBIGERAJCUYgguOAhUECAKIIOAAwAQiABJFABIAAA==}#}#}}
27.(本小题满分 14分)综合与实践
【问题初探】(1)某兴趣小组探索这样一个问题:若 AD是△ABC的角平分线,则线段
AB、AC、BD、CD有何数量关系?下面是小智、小勇的部分思路和方法,请完成填空:
小智的思路和方法: 小勇的思路和方法:
如图 1,作 DM⊥AB,DN⊥AC,垂足分 如图 2,作 CE∥AB,交 AD的延长线于
别为 M、N. 点 E. A
∵AD平分∠BAC,DM⊥AB,DN⊥AC, ∵AD平分∠BAC,
∴ ▲ . A ∴∠BAD=∠CAD.
1 ∵CE∥AB,
∵ S ABD= AB DM,
B D C
2 ∴∠BAD=∠E.
M
1 N ∴∠CAD=∠E.S ACD= AC DN, E2 ∴ ▲ . 图 2
S ABD AB
B D C
∴ . 再通过证明△CDE∽△BDA得到比例式,=
S AC 图 1 ACD 从而推导出结论……
再用另一种方式表示△ABD与△ACD的
面积,即可推导出结论……
根据小智或小勇的方法,可以得到线段 AB、AC、BD、CD的数量关系是 ▲ .
【变式拓展】(2)小慧对问题作了进一步拓展:如图 3,在△ABC中,AB=AC,D是 BC
边上一点,∠BAD=45°,∠CAD=60°,求 BD的值.请你完成解答.
CD A
A
D E
B D C E F B C
图 3 图 4 图 5
【迁移应用】(3)请你借助以上结论或方法,用无刻度直尺和圆规在图 4的线段 EF上作
一点 P,使 EP 3FP.(要求:不写作法,保留作图痕迹)
【综合提升】(4)如图 5,在△ABC中,AB=5,AC=4, BAC= ( <90°),点 D
在 AC边上,CD=1,点 E在 BD的延长线上,连接 EC, BEC= ( < ),请直接写出
BD DE的值(用含 , 的式子表示).
数学试题 第 6页(共 6页)
{#{QQABQYwy1U4owgAgwgAgNIJYAACBTh5CbQQw0n2ooCAQAsQkBIGERAJCUYgguOAhUECAKIIOAAwAQiABJFABIAAA==}#}#}}
同课章节目录
