人教版八年级数学下册第十九章 一次函数 复习课(共30张PPT)
文档属性
| 名称 | 人教版八年级数学下册第十九章 一次函数 复习课(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-12 20:41:37 | ||
图片预览







文档简介
(共30张PPT)
一次函数复习课
在一个变化过程中,如果有两个变量
x与y,并且对于x的每一个确定的值,y都有唯 一确定的值与其对应,那么我们就说x是自变量 ,y是x的函数。
一、函数的概念:
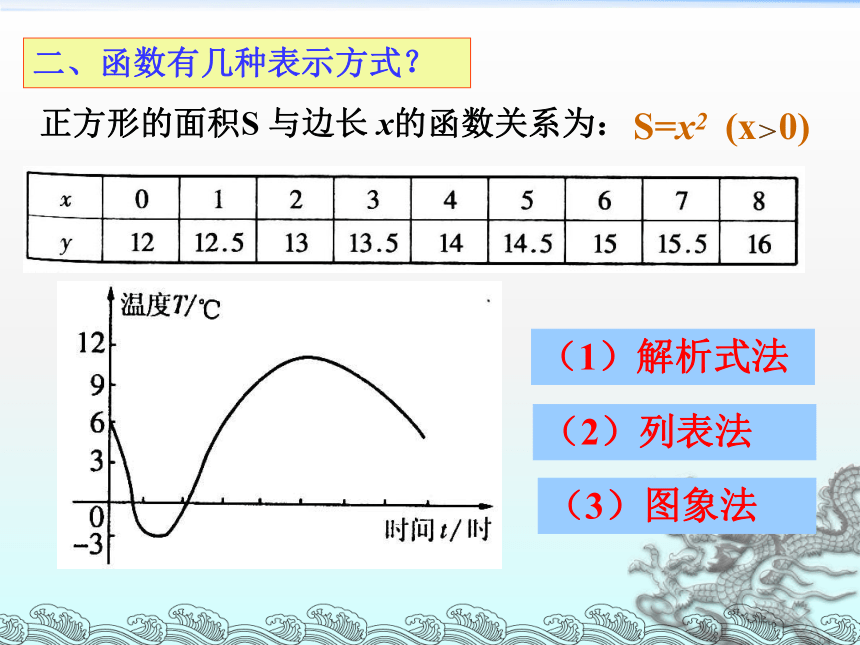
(1)解析式法
(2)列表法
(3)图象法
正方形的面积S 与边长 x的函数关系为:
S=x2
(x>0)
二、函数有几种表示方式?
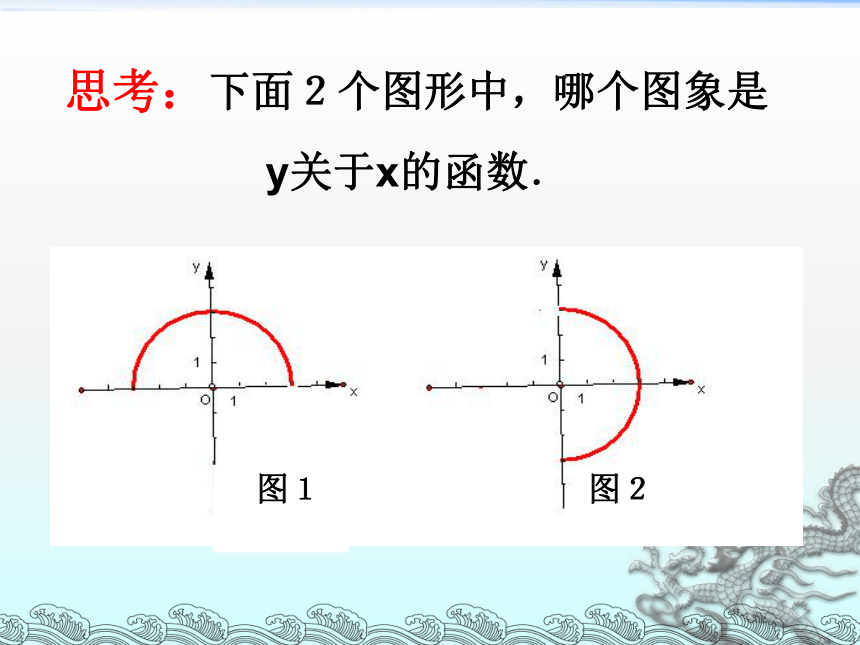
思考:下面2个图形中,哪个图象是
y关于x的函数.
图1
图2
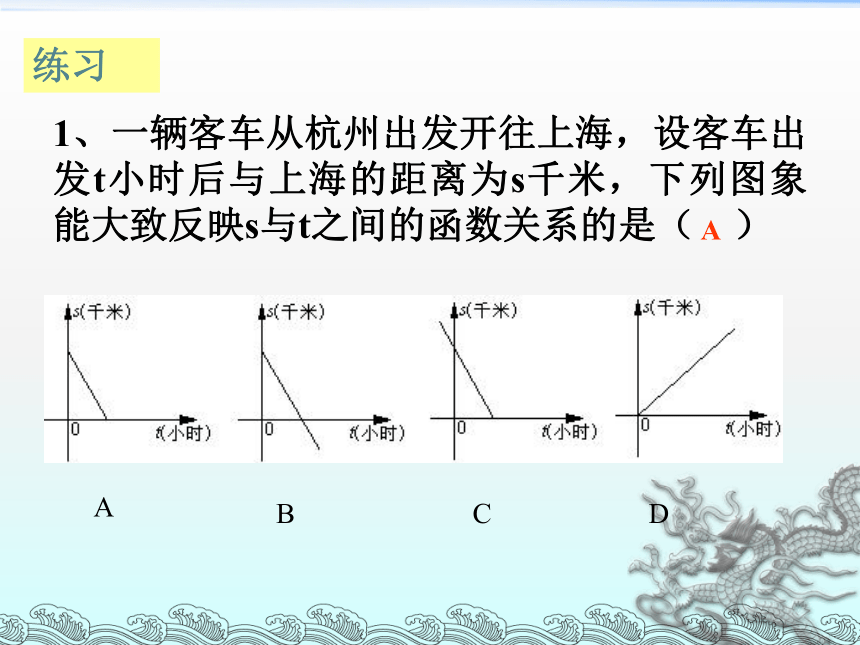
1、一辆客车从杭州出发开往上海,设客车出发t小时后与上海的距离为s千米,下列图象能大致反映s与t之间的函数关系的是( )
A
B
C
D
A
练习
2.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车。车修好后,因怕耽误上课,他比修车前加快了骑车速度匀速行驶。下面是行驶路程s(米)关于时间t(分)的函数图像,那么符合这个同学行驶情况的图像大致是 ( )
A B C D
C
求出下列函数中自变量的取值范围
三、自变量的取值范围
分式的分母不为0
被开方数(式)为非负数
与实际问题有关系的,应使实际问题有意义
x 0 0.5 1 1.5 2 2.5 3
s 0
0.25
1
2.25
4
6.25
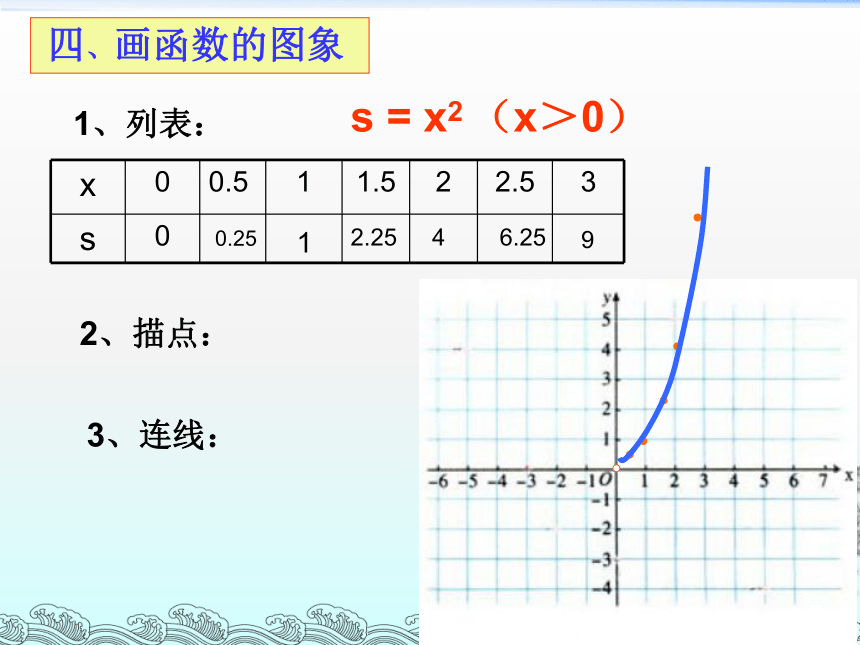
9
1、列表:
2、描点:
3、连线:
四、画函数的图象
s = x2 (x>0)
一次函数的概念:函数y=_______
(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
kx +b
≠0
=0
≠0
思 考
kx
y=k xn +b为一次函数的条件是什么
五、正比例函数与一次函数的概念:
2:函数y=(m +2)x+( -4)为正比例
函数,则m为何值
1.下列函数中,哪些是一次函数
m =2
答:
(1)是 (2)不是 (3)是 (4)不是
练习
k>0
图象过一、三象限和原点
k<0
b=0
b>0
图象过一、二、三象限
b<0
图象过一、三、四象限
b=0
图象过二、四象限和原点
b>0
图象过一、二 、四象限
b<0
图象过二、三 、四象限
y随x的增大而增大
y随x的增大而减少
.
b
.
b
.
b
.
b
.
b
.
b
六、一次函数与正比例函数的图象与性质
x
y
o
x
y
o
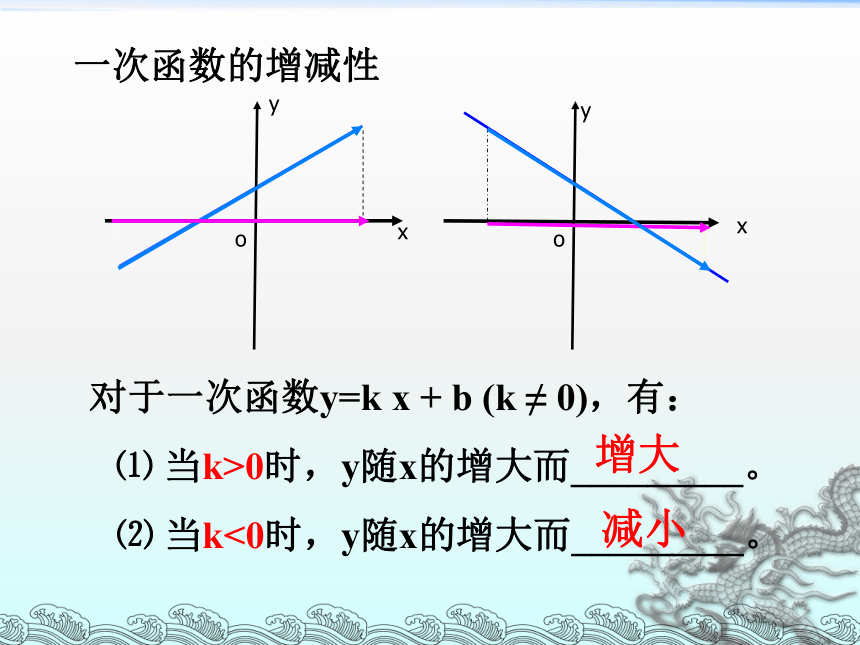
一次函数的增减性
对于一次函数y=k x + b (k ≠ 0),有:
⑴ 当k>0时,y随x的增大而_________。
⑵ 当k<0时,y随x的增大而_________。
增大
减小
1. 填空题:
有下列函数:① , ② ,
③ , ④ 。其中过原点的直
线是_____;函数y随x的增大而增大的是________;函数y随x的增大而减小的是______;图象在第一、二、三象限的是_____。
练习
x
y
2
=
②
①、②、③
④
③
2.根据下列一次函数y=kx+b(k ≠ 0)的草图回 答出各图中k、b的符号:
k__0,b__0 k__0,b__0 k__0,b__0 k__0,b__0
<
>
<
>
>
>
<
<
3、直线y=kx+b经过一、二、四象限,则
K 0, b 0.
<
>
此时,直线y=bx+k的图象只能是( )
D
4、设点P(0,m),Q(n,2)都在函数y=x+b的图象上,求m+n的值
5、y=-x+2与x轴交点坐标( ),
y轴交点坐标( )
0,2
2,0
6、已知一次函数y=(m+2)x+(m-3), 当m分别取
什么值时,(1)y随x值的增大而减小
(2)图象过原点
(3)图象与y轴的交点x在轴的下方
(4)图象不经过第二象限?
解: 根据题意,得:
∵y随x值的增大而减小
∴m+2﹤0
∴m ﹤-2
(3) ∵图象与y轴的交点
在x轴的下方
∴m-3﹤0
∴m﹤3
(4)∵图象不经过第二象限
怎样画一次函数y=kx+b的图象?
1、两点法
y=x+1
2、平移法
七、求函数解析式的方法:
先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法, --待定系数法
例1、如图,直线a是一次函数y=kx+b的图象,
求其解析式
点评:求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。
y
-2
-1
x
o
a
解:由图象知直线过(-2,0),(0,-1)两点
把两点的坐标分别代入y=kx+b,得:
-2k+b=0
b=-1
解得:k= - 0.5,b=-1
∴其函数解析式为y= - 0.5x-1
例2、已知y与x-1成正比例,x=8时,y=6,写出y与x之间函数关系式,并分别求出x=4时y的值和y =-3时x的值。
解:由 y与x-1成正比例可设y=k(x-1)
∵ 当x=8时,y=6
∴7k=6 ∴
∴ y与x之间函数关系式是:
例3、若函数y=kx+b的图象平行于y= -2x的图象且经过点(0,4), 则直线y=kx+b与两坐标轴围成的三角形的面积是:
解:∵y=kx+b图象与y= - 2x图象平行
∴k=-2
∵图像经过点(0,4)
∴b=4
∴此函数的解析式为y= - 2x+4
∵函数y= - 2x+4与两坐标轴的交点为
(0,4)和(2,0)
1、已知直线y=kx+b平行与直线y=-2x,且与y轴交于点(0,-2),则k=___,b=___.
此时,直线y=kx+b可以由直线y=-2x经过怎样平移得到?
-2
-2
练习:
2、若一次函数y=x+b的图象过点A(1,-1),则b=__________。
3、根据如图所示的条件,求直线的表达式。
-2
沿y轴向下平移2个单位
y=2x
4、柴油机在工作时油箱中的余油量Q(千克)与工作时间t(小时)成一次函数关系,当工作开始时油箱中有油40千克,工作3.5小时后,油箱中余油22.5千克
(1)写出余油量Q与时间t的函数关系式.
解:(1)设所求函数关系式为:Q=kt+b。
把t=0,Q=40;t=3.5,Q=22.5分别代入上式,得
解得
解析式为:Q=-5t+40
(0≤t≤8)
4、柴油机在工作时油箱中的余油量Q(千克)与工作时间t(小时)成一次函数关系,当工作开始时油箱中有油40千克,工作3.5小时后,油箱中余油22.5千克
(1)写出余油量Q与时间t的函数关系式.
(2)取t=0,得Q=40;取t=8,得Q=0描出点A(0,40),B(8,0)。然后连成线段AB即是所求的图形。
注意:(1)求出函数关系式时,必须找出自变量的取值范围。
(2)画函数图象时,应根据函数自变量的取值范围来确定图象的范围。
图象是包括
两端点的线段
.
20
40
8
0
t
Q
.
A
B
(2)画出这个函数的图象。
Q=-5t+40
(0≤t≤8)
5、某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(1)服药后______时,血
液中含药量最高,达到每
毫升_______毫克,接着逐
步衰弱。
(2)服药5时,血液中含药
量为每毫升____毫克。
x/时
y/毫克
6
3
2
5
O
2
6
3
(3)当x≤2时y与x之间的函数关系式是___________。
(4)当x≥2时y与x之间的函数关系式是___________。
(5)如果每毫升血液中含
药量3毫克或3毫克以上时,
治疗疾病最有效,那么这
个有效时间是___时。
x/时
y/毫克
6
3
2
5
O
y=3x
y=-x+8
4
1.在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间 x(h)之间的关系如图所示.
挑战自我
(1)甲、乙两根蜡烛燃烧前的高度分别是_________,从点燃到燃尽所用的时间分别是__________;
30cm,25cm
2h , 2.5h
(2)当x=___时,甲、乙两根蜡烛在燃烧过程中的高度相等.当x 时,
1h
甲蜡烛比乙蜡烛高,当x 时,甲蜡烛比乙蜡烛低。
013.如图,表示甲骑电动自行车和乙驾驶汽车均行驶90km过程中,行驶的路程y与经过的时间x之间的函数关系.请根据图象填空: 出发的早,早了 小时, 先到达,先到 小时,电动自行车的速度为 km/h,汽车的速度为 km/h.
电动自行车
2
汽车
2
18
90
2.函数 的图像与x轴交点A 的坐标为_____,与y轴交点B的坐标为_____,△AOB的面积为__.
(0,4)
(-6,0)
12
第3题图
(1)l1对应的表达是 ,l2对应的表达式是 。
( 2)当销售量为2吨时,销售收入= 元,销售成本= 元。
(3)当销售量为6吨时,销售收入
= 元,销售成本= 元。
(4)当销售量等于 吨时,销售收入等于销售成本。
(5)当销售量 吨时,该公司盈利(收入大于成本)。
当销售 吨时,该公司亏损(收入小于成本)。
4、如图所示l1反映了该公司产品的销售成本与销售量的关系, l2反映了某公司产品的销售收入与销售量的关系。根据图意填空:
Y=500x+2000
Y=1000x
2000
3000
4
大于4
小于4
6000
5000
5.小聪上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中。小聪离家的路程s(km)和所经过的时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:
(1)小聪去超市途中的速度是多少?回家途中的速度是多少?
0
(2)小聪在超市逗留了多少时间?
(3)用恰当的方式表示路程s与时间t之间的关系。
(4)小聪在来去途中,离家1km处的时间是几时几分?
一次函数复习课
在一个变化过程中,如果有两个变量
x与y,并且对于x的每一个确定的值,y都有唯 一确定的值与其对应,那么我们就说x是自变量 ,y是x的函数。
一、函数的概念:
(1)解析式法
(2)列表法
(3)图象法
正方形的面积S 与边长 x的函数关系为:
S=x2
(x>0)
二、函数有几种表示方式?
思考:下面2个图形中,哪个图象是
y关于x的函数.
图1
图2
1、一辆客车从杭州出发开往上海,设客车出发t小时后与上海的距离为s千米,下列图象能大致反映s与t之间的函数关系的是( )
A
B
C
D
A
练习
2.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车。车修好后,因怕耽误上课,他比修车前加快了骑车速度匀速行驶。下面是行驶路程s(米)关于时间t(分)的函数图像,那么符合这个同学行驶情况的图像大致是 ( )
A B C D
C
求出下列函数中自变量的取值范围
三、自变量的取值范围
分式的分母不为0
被开方数(式)为非负数
与实际问题有关系的,应使实际问题有意义
x 0 0.5 1 1.5 2 2.5 3
s 0
0.25
1
2.25
4
6.25
9
1、列表:
2、描点:
3、连线:
四、画函数的图象
s = x2 (x>0)
一次函数的概念:函数y=_______
(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
kx +b
≠0
=0
≠0
思 考
kx
y=k xn +b为一次函数的条件是什么
五、正比例函数与一次函数的概念:
2:函数y=(m +2)x+( -4)为正比例
函数,则m为何值
1.下列函数中,哪些是一次函数
m =2
答:
(1)是 (2)不是 (3)是 (4)不是
练习
k>0
图象过一、三象限和原点
k<0
b=0
b>0
图象过一、二、三象限
b<0
图象过一、三、四象限
b=0
图象过二、四象限和原点
b>0
图象过一、二 、四象限
b<0
图象过二、三 、四象限
y随x的增大而增大
y随x的增大而减少
.
b
.
b
.
b
.
b
.
b
.
b
六、一次函数与正比例函数的图象与性质
x
y
o
x
y
o
一次函数的增减性
对于一次函数y=k x + b (k ≠ 0),有:
⑴ 当k>0时,y随x的增大而_________。
⑵ 当k<0时,y随x的增大而_________。
增大
减小
1. 填空题:
有下列函数:① , ② ,
③ , ④ 。其中过原点的直
线是_____;函数y随x的增大而增大的是________;函数y随x的增大而减小的是______;图象在第一、二、三象限的是_____。
练习
x
y
2
=
②
①、②、③
④
③
2.根据下列一次函数y=kx+b(k ≠ 0)的草图回 答出各图中k、b的符号:
k__0,b__0 k__0,b__0 k__0,b__0 k__0,b__0
<
>
<
>
>
>
<
<
3、直线y=kx+b经过一、二、四象限,则
K 0, b 0.
<
>
此时,直线y=bx+k的图象只能是( )
D
4、设点P(0,m),Q(n,2)都在函数y=x+b的图象上,求m+n的值
5、y=-x+2与x轴交点坐标( ),
y轴交点坐标( )
0,2
2,0
6、已知一次函数y=(m+2)x+(m-3), 当m分别取
什么值时,(1)y随x值的增大而减小
(2)图象过原点
(3)图象与y轴的交点x在轴的下方
(4)图象不经过第二象限?
解: 根据题意,得:
∵y随x值的增大而减小
∴m+2﹤0
∴m ﹤-2
(3) ∵图象与y轴的交点
在x轴的下方
∴m-3﹤0
∴m﹤3
(4)∵图象不经过第二象限
怎样画一次函数y=kx+b的图象?
1、两点法
y=x+1
2、平移法
七、求函数解析式的方法:
先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法, --待定系数法
例1、如图,直线a是一次函数y=kx+b的图象,
求其解析式
点评:求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。
y
-2
-1
x
o
a
解:由图象知直线过(-2,0),(0,-1)两点
把两点的坐标分别代入y=kx+b,得:
-2k+b=0
b=-1
解得:k= - 0.5,b=-1
∴其函数解析式为y= - 0.5x-1
例2、已知y与x-1成正比例,x=8时,y=6,写出y与x之间函数关系式,并分别求出x=4时y的值和y =-3时x的值。
解:由 y与x-1成正比例可设y=k(x-1)
∵ 当x=8时,y=6
∴7k=6 ∴
∴ y与x之间函数关系式是:
例3、若函数y=kx+b的图象平行于y= -2x的图象且经过点(0,4), 则直线y=kx+b与两坐标轴围成的三角形的面积是:
解:∵y=kx+b图象与y= - 2x图象平行
∴k=-2
∵图像经过点(0,4)
∴b=4
∴此函数的解析式为y= - 2x+4
∵函数y= - 2x+4与两坐标轴的交点为
(0,4)和(2,0)
1、已知直线y=kx+b平行与直线y=-2x,且与y轴交于点(0,-2),则k=___,b=___.
此时,直线y=kx+b可以由直线y=-2x经过怎样平移得到?
-2
-2
练习:
2、若一次函数y=x+b的图象过点A(1,-1),则b=__________。
3、根据如图所示的条件,求直线的表达式。
-2
沿y轴向下平移2个单位
y=2x
4、柴油机在工作时油箱中的余油量Q(千克)与工作时间t(小时)成一次函数关系,当工作开始时油箱中有油40千克,工作3.5小时后,油箱中余油22.5千克
(1)写出余油量Q与时间t的函数关系式.
解:(1)设所求函数关系式为:Q=kt+b。
把t=0,Q=40;t=3.5,Q=22.5分别代入上式,得
解得
解析式为:Q=-5t+40
(0≤t≤8)
4、柴油机在工作时油箱中的余油量Q(千克)与工作时间t(小时)成一次函数关系,当工作开始时油箱中有油40千克,工作3.5小时后,油箱中余油22.5千克
(1)写出余油量Q与时间t的函数关系式.
(2)取t=0,得Q=40;取t=8,得Q=0描出点A(0,40),B(8,0)。然后连成线段AB即是所求的图形。
注意:(1)求出函数关系式时,必须找出自变量的取值范围。
(2)画函数图象时,应根据函数自变量的取值范围来确定图象的范围。
图象是包括
两端点的线段
.
20
40
8
0
t
Q
.
A
B
(2)画出这个函数的图象。
Q=-5t+40
(0≤t≤8)
5、某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(1)服药后______时,血
液中含药量最高,达到每
毫升_______毫克,接着逐
步衰弱。
(2)服药5时,血液中含药
量为每毫升____毫克。
x/时
y/毫克
6
3
2
5
O
2
6
3
(3)当x≤2时y与x之间的函数关系式是___________。
(4)当x≥2时y与x之间的函数关系式是___________。
(5)如果每毫升血液中含
药量3毫克或3毫克以上时,
治疗疾病最有效,那么这
个有效时间是___时。
x/时
y/毫克
6
3
2
5
O
y=3x
y=-x+8
4
1.在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间 x(h)之间的关系如图所示.
挑战自我
(1)甲、乙两根蜡烛燃烧前的高度分别是_________,从点燃到燃尽所用的时间分别是__________;
30cm,25cm
2h , 2.5h
(2)当x=___时,甲、乙两根蜡烛在燃烧过程中的高度相等.当x 时,
1h
甲蜡烛比乙蜡烛高,当x 时,甲蜡烛比乙蜡烛低。
0
电动自行车
2
汽车
2
18
90
2.函数 的图像与x轴交点A 的坐标为_____,与y轴交点B的坐标为_____,△AOB的面积为__.
(0,4)
(-6,0)
12
第3题图
(1)l1对应的表达是 ,l2对应的表达式是 。
( 2)当销售量为2吨时,销售收入= 元,销售成本= 元。
(3)当销售量为6吨时,销售收入
= 元,销售成本= 元。
(4)当销售量等于 吨时,销售收入等于销售成本。
(5)当销售量 吨时,该公司盈利(收入大于成本)。
当销售 吨时,该公司亏损(收入小于成本)。
4、如图所示l1反映了该公司产品的销售成本与销售量的关系, l2反映了某公司产品的销售收入与销售量的关系。根据图意填空:
Y=500x+2000
Y=1000x
2000
3000
4
大于4
小于4
6000
5000
5.小聪上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中。小聪离家的路程s(km)和所经过的时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:
(1)小聪去超市途中的速度是多少?回家途中的速度是多少?
0
(2)小聪在超市逗留了多少时间?
(3)用恰当的方式表示路程s与时间t之间的关系。
(4)小聪在来去途中,离家1km处的时间是几时几分?
