2.2.1直线的点斜式方程 课件(共16张PPT)
文档属性
| 名称 | 2.2.1直线的点斜式方程 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-12 16:54:16 | ||
图片预览




文档简介
(共16张PPT)
2.2.1 直线的点斜式方程
第二章 直线与圆的方程
教学目标
1.能根据确定直线位置的几何要素,探索直线的点斜式方程
2.掌握直线方程的点斜式和斜截式,并会熟练应用
3.了解截距的概念,了解直线的斜截式方程与一次函数的关系
4.会用直线的点斜式方程和斜截式方程解决直线的平行与垂直问题
问题与例题
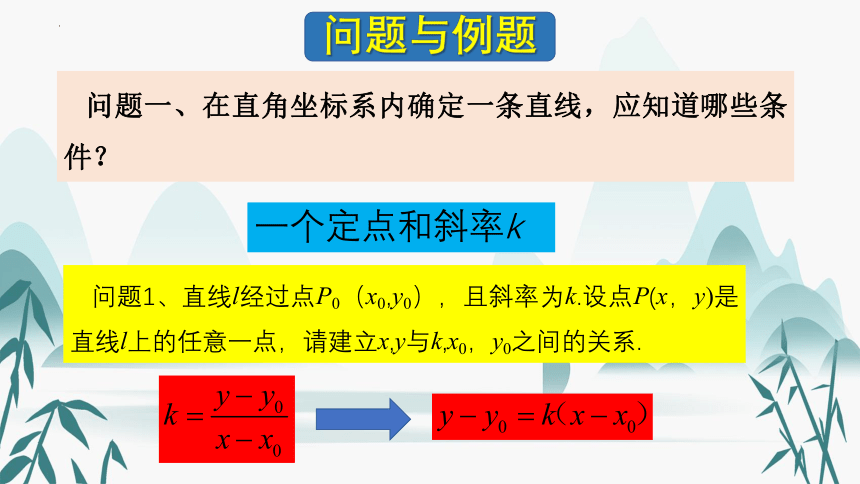
问题一、在直角坐标系内确定一条直线,应知道哪些条件?
问题1、直线l经过点P0(x0,y0),且斜率为k.设点P(x,y)是直线l上的任意一点,请建立x,y与k,x0,y0之间的关系.
一个定点和斜率k
问题2、过点P0(x0,y0),斜率是k的直线l上的点,其坐标都满足方程吗?坐标满足方程的点都在经过P0(x0,y0),斜率为k的直线上吗?
(1)直线l上每一个点的坐标(x,y)都满足关系式y-y0=k(x-x0);
(2)若点P1(x1,y1)的坐标x1,y1满足关系式y-y0=k(x-x0),则
y1-y0=k(x1-x0)
当x1=x0时,y1=y0,这时点P1与P0重合,显然有点P1在直线l上;
当x1≠x0时,有 ,这表明P、P1、P0重合在一条直线上;
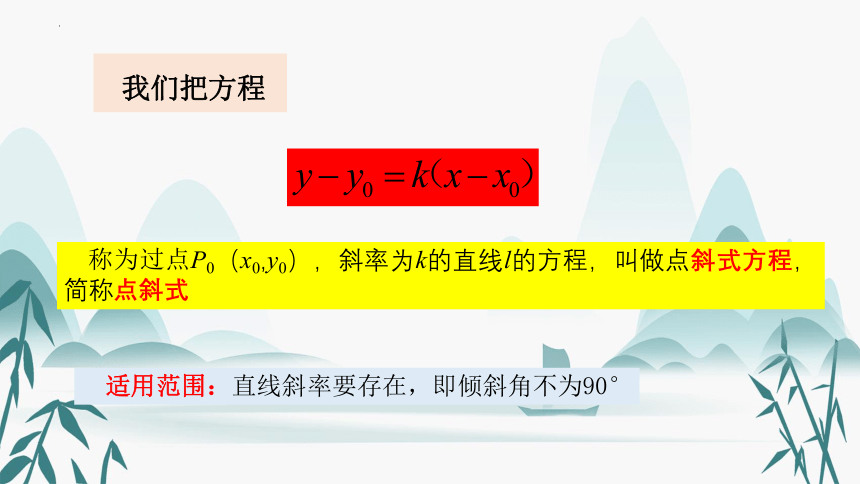
我们把方程
称为过点P0(x0,y0),斜率为k的直线l的方程,叫做点斜式方程,简称点斜式
适用范围:直线斜率要存在,即倾斜角不为90°
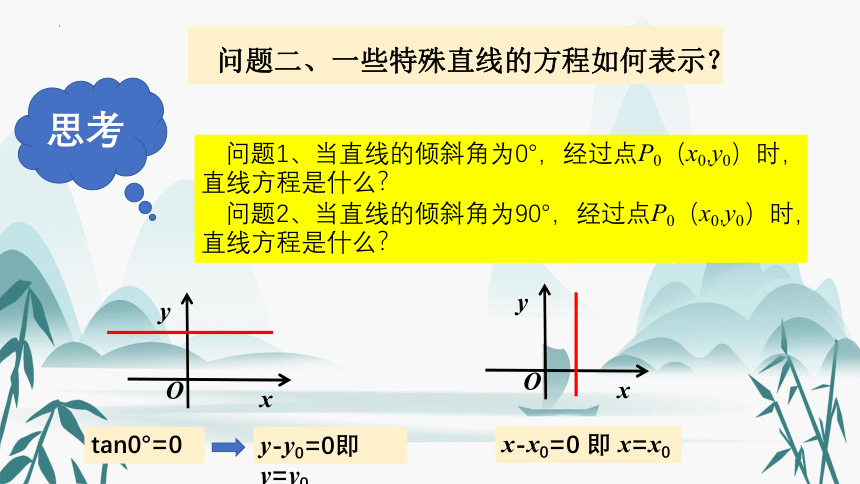
问题二、一些特殊直线的方程如何表示?
问题1、当直线的倾斜角为0°,经过点P0(x0,y0)时,直线方程是什么?
问题2、当直线的倾斜角为90°,经过点P0(x0,y0)时,直线方程是什么?
思考
x
y
O
x
y
O
tan0°=0
y-y0=0即y=y0
x-x0=0 即 x=x0
例题1、直线l经过点p(-2,3),且倾斜角α=45°,求直线l的点斜式方程,并画出直线l。
解:直线的斜率k=tan45°=1
将点P与k带入方程得:
y-3=x+2
x
y
O
变式练习
写出下列直线的点斜式方程
(1)经过点A(3,-1),斜率是;
(2)经过点,倾斜角是30°;
(3)经过点C(0,3),倾斜角是0°
由点斜式方程得:
问题三、已知直线l的斜率为k,且与y轴的交点为(0,b),求直线l的方程。
即:
斜截式
直线l在y轴上的截距
截距是距离吗?
不是,截距可正、可负、可为0
例2、一条直线经过点P1(0,3),斜率为2,求这条直线的方程.
解:由直线的斜截式得
y=2x+3
1、在例1中,若将“斜率为2”改为“倾斜角为45°”,求这条直线的方程;
2、在例1中,若将直线的倾斜角改为90°,这条直线的方程是什么?
3、方程 表示过点 、斜率是 、倾斜角是 、在y轴上的截距是 的直线.
变式练习
例题4、已知直线l1:y=k1x+b1,l2:y=k2x+b2,试讨论:
(1)l1∥l2的条件是什么?
(2)l1⊥l2的条件是什么?
判断下列各直线是否平行或垂直
变式练习
课堂小结
1.本节课我们学过那些知识点;
2.直线方程的点斜式、斜截式的形式特点和适用范围是什么?
3.求一条直线的方程,要知道多少个条件?
课后作业
教材P61 练习
谢谢!
2.2.1 直线的点斜式方程
第二章 直线与圆的方程
教学目标
1.能根据确定直线位置的几何要素,探索直线的点斜式方程
2.掌握直线方程的点斜式和斜截式,并会熟练应用
3.了解截距的概念,了解直线的斜截式方程与一次函数的关系
4.会用直线的点斜式方程和斜截式方程解决直线的平行与垂直问题
问题与例题
问题一、在直角坐标系内确定一条直线,应知道哪些条件?
问题1、直线l经过点P0(x0,y0),且斜率为k.设点P(x,y)是直线l上的任意一点,请建立x,y与k,x0,y0之间的关系.
一个定点和斜率k
问题2、过点P0(x0,y0),斜率是k的直线l上的点,其坐标都满足方程吗?坐标满足方程的点都在经过P0(x0,y0),斜率为k的直线上吗?
(1)直线l上每一个点的坐标(x,y)都满足关系式y-y0=k(x-x0);
(2)若点P1(x1,y1)的坐标x1,y1满足关系式y-y0=k(x-x0),则
y1-y0=k(x1-x0)
当x1=x0时,y1=y0,这时点P1与P0重合,显然有点P1在直线l上;
当x1≠x0时,有 ,这表明P、P1、P0重合在一条直线上;
我们把方程
称为过点P0(x0,y0),斜率为k的直线l的方程,叫做点斜式方程,简称点斜式
适用范围:直线斜率要存在,即倾斜角不为90°
问题二、一些特殊直线的方程如何表示?
问题1、当直线的倾斜角为0°,经过点P0(x0,y0)时,直线方程是什么?
问题2、当直线的倾斜角为90°,经过点P0(x0,y0)时,直线方程是什么?
思考
x
y
O
x
y
O
tan0°=0
y-y0=0即y=y0
x-x0=0 即 x=x0
例题1、直线l经过点p(-2,3),且倾斜角α=45°,求直线l的点斜式方程,并画出直线l。
解:直线的斜率k=tan45°=1
将点P与k带入方程得:
y-3=x+2
x
y
O
变式练习
写出下列直线的点斜式方程
(1)经过点A(3,-1),斜率是;
(2)经过点,倾斜角是30°;
(3)经过点C(0,3),倾斜角是0°
由点斜式方程得:
问题三、已知直线l的斜率为k,且与y轴的交点为(0,b),求直线l的方程。
即:
斜截式
直线l在y轴上的截距
截距是距离吗?
不是,截距可正、可负、可为0
例2、一条直线经过点P1(0,3),斜率为2,求这条直线的方程.
解:由直线的斜截式得
y=2x+3
1、在例1中,若将“斜率为2”改为“倾斜角为45°”,求这条直线的方程;
2、在例1中,若将直线的倾斜角改为90°,这条直线的方程是什么?
3、方程 表示过点 、斜率是 、倾斜角是 、在y轴上的截距是 的直线.
变式练习
例题4、已知直线l1:y=k1x+b1,l2:y=k2x+b2,试讨论:
(1)l1∥l2的条件是什么?
(2)l1⊥l2的条件是什么?
判断下列各直线是否平行或垂直
变式练习
课堂小结
1.本节课我们学过那些知识点;
2.直线方程的点斜式、斜截式的形式特点和适用范围是什么?
3.求一条直线的方程,要知道多少个条件?
课后作业
教材P61 练习
谢谢!
