人教版数学九年级上册22.1.2二次函数y=ax2的图象和性质 课件(共18张PPT)
文档属性
| 名称 | 人教版数学九年级上册22.1.2二次函数y=ax2的图象和性质 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-13 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
22.1.2二次函数y=ax2的图象和性质
(第一课时)
九年级 上册
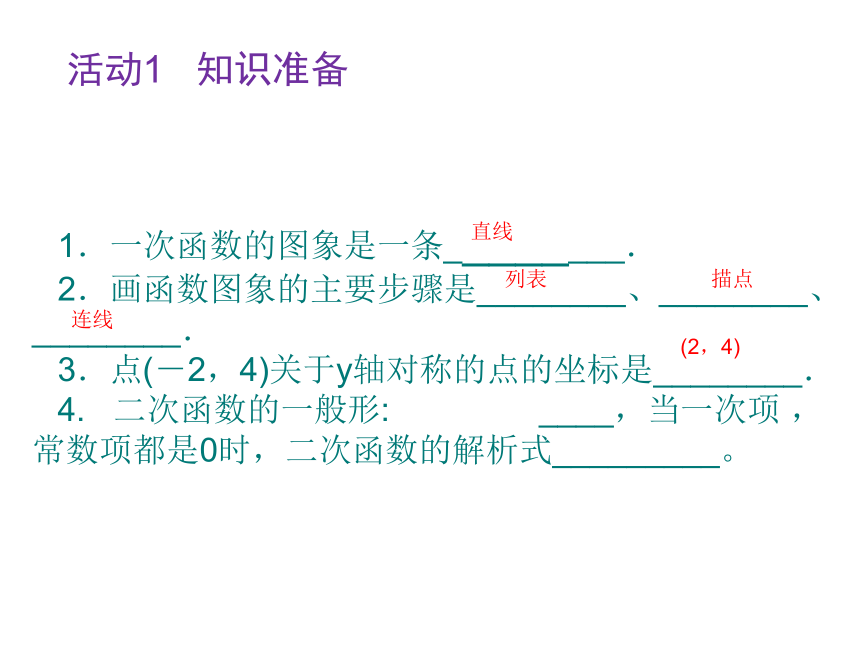
活动1 知识准备
1.一次函数的图象是一条________.
2.画函数图象的主要步骤是________、________、 ________.
3.点(-2,4)关于y轴对称的点的坐标是________.
4. 二次函数的一般形: ____,当一次项 ,常数项都是0时,二次函数的解析式_________。
直线
列表
描点
连线
(2,4)
数形结合,直观感受
观察y=x2,选择适当的x值,并计算相应的y值,完成下表:
用描点法画二次函数y=x2的图象
x
y=x2
x … -3 -2 -1 0 1 2 3 …
y=x2
x
y=x2 … 9 4 1 0 1 4 9 …
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
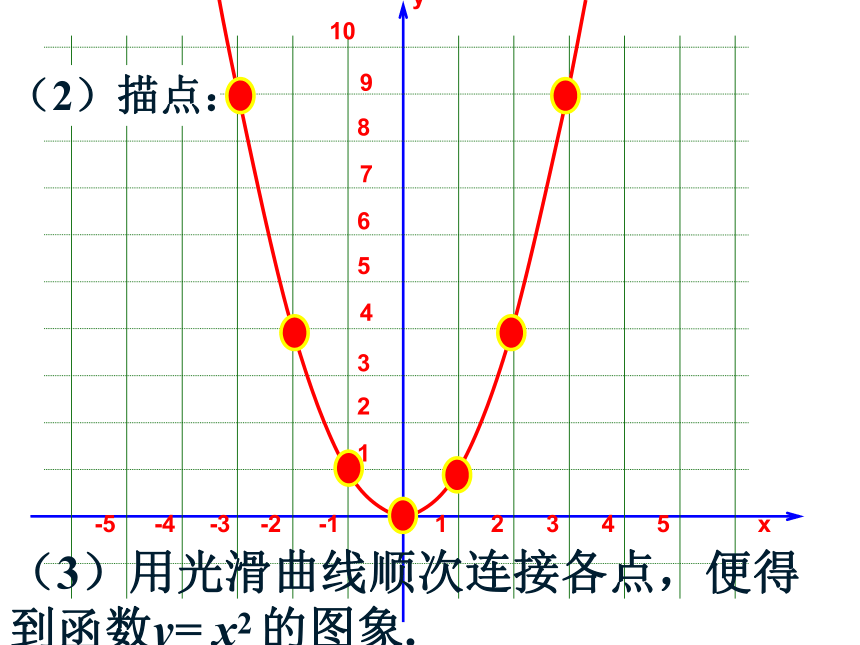
(2)描点:
(3)用光滑曲线顺次连接各点,便得到函数y= x2 的图象.
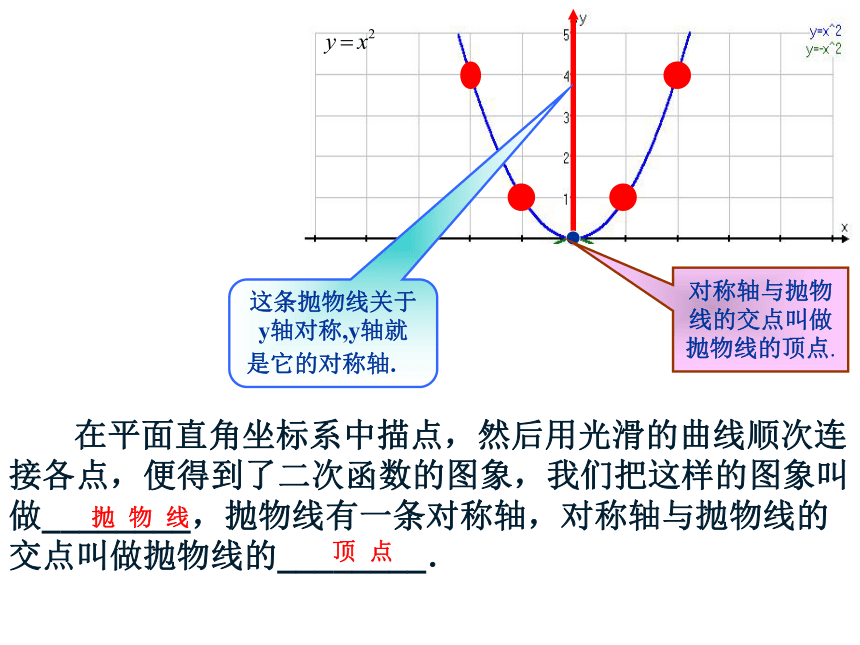
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴与抛物
线的交点叫做
抛物线的顶点.
在平面直角坐标系中描点,然后用光滑的曲线顺次连接各点,便得到了二次函数的图象,我们把这样的图象叫做________,抛物线有一条对称轴,对称轴与抛物线的交点叫做抛物线的________.
抛 物 线
顶 点
22.1.2 二次函数y=ax 的图象和性质
2
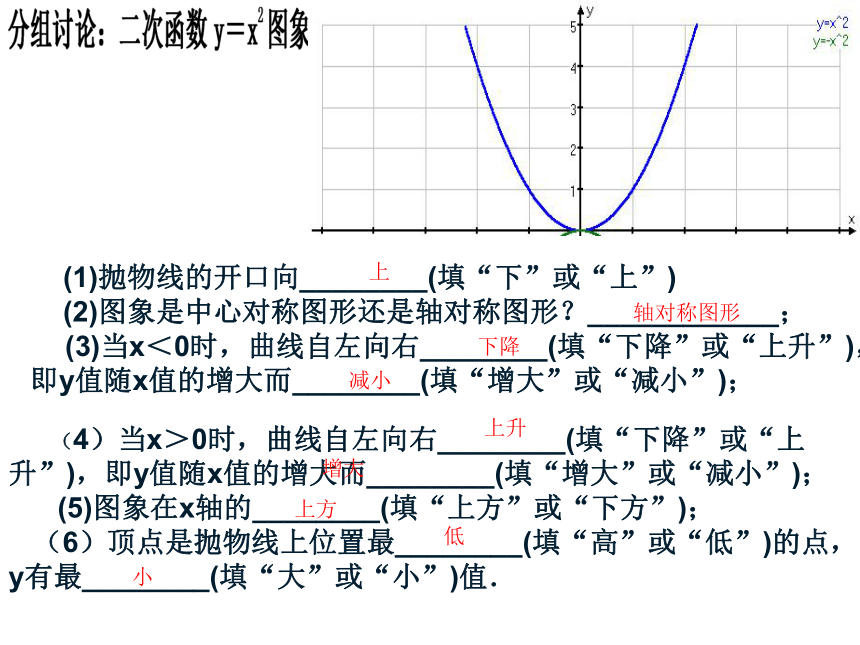
(1)抛物线的开口向________(填“下”或“上”)
(2)图象是中心对称图形还是轴对称图形?____________;
(3)当x<0时,曲线自左向右________(填“下降”或“上升”), 即y值随x值的增大而________(填“增大”或“减小”);
上
轴对称图形
下降
减小
(4)当x>0时,曲线自左向右________(填“下降”或“上升”),即y值随x值的增大而________(填“增大”或“减小”);
(5)图象在x轴的________(填“上方”或“下方”);
(6)顶点是抛物线上位置最________(填“高”或“低”)的点,y有最________(填“大”或“小”)值.
上升
增大
上方
低
小
x … -4 -3 -2 -1 0 1 2 3 4 …
y= x2
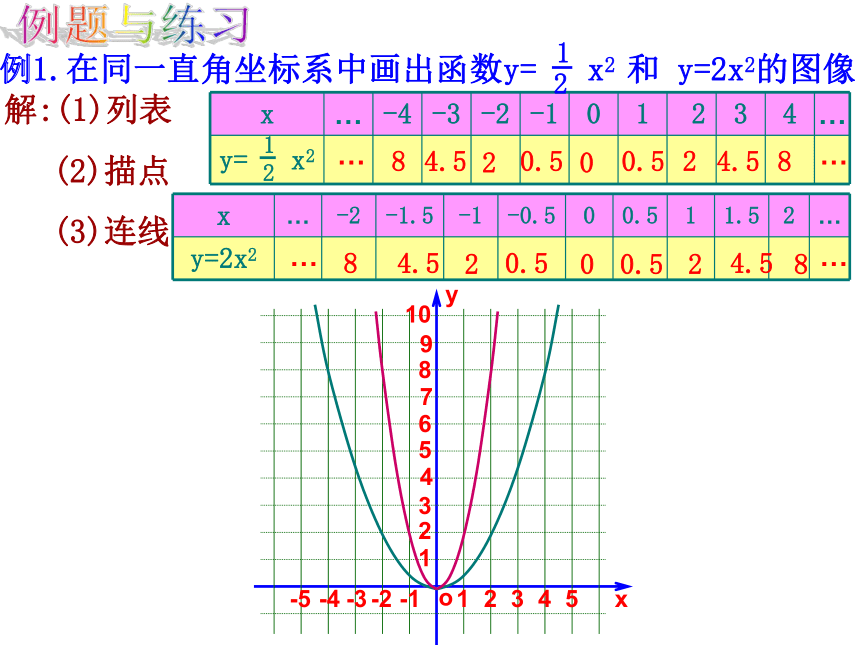
例1.在同一直角坐标系中画出函数y= x2 和 y=2x2的图像
解:(1)列表
(2)描点
(3)连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
1
2
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=2x2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
1
2
共同点:
不同点:
开口向上,顶点是原点,顶点是抛物线的最低点,对称轴是y轴,
除顶点外,图像都在x轴上方
开口大小不同
函数y= x2,y=2x2的图像与函数y=x2的图像相比,有什么共同点和不同点
1
2
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y=x2
y= 2x2
y= 0.5x2
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
在同一直角坐标系中画出函数y=- x2和y=-2x2的图像
1
2
y=- x2
1
2
y=-2x2
x
…
-4
-3
-2
-1
0
1
2
3
4
…
y=- x2
…
…
0
-2
-2
-8
-8
x
…
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
…
y=-2x2
…
…
0
-2
-2
-8
-8
函数y=- x2,y=-2x2的图像与y=-x2的图像相比,有什么共同点和不同点
1
2
共同点:
不同点:
开口向下,顶点是原点,对称轴是y轴,顶点是抛物线的最高点
除顶点外,图像都在x轴下方
开口大小不同
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
y=- x2
1
2
y=-2x2
y=-x2
A的取值
顶点坐标
对称轴
位置
开口方向
增减性
最值
a>0
a<0
(0,0)
(0,0)
Y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,y有最小值为0.
当x=0时, y有最大值为0.
当x<0时,y随着x的增大而减小.
在当x>0时, y随着x的增大而增大.
当x<0时,y随着x的增大而增大.
在x>0时, y随着x的增大而减小.
二次函数y=ax2的性质
︱a︱的越大,开口越小。
开口大小
说出下列抛物线的开口方向、对称轴和顶点:
(1) ;
(2) ;
(3) ;
(4) .
1.巩固练习
开口向上、y 轴、原点.
开口向下、y 轴、原点.
开口向上、y 轴、原点.
开口向下、y 轴、原点.
2.在同一坐标系中,图象与 的图象
关于 轴对称的函数为( ).
(A)
(B)
(C)
(D)
C
巩固练习
巩固练习
2.抛物线
共有的性质是( ).
(A)开口向上
(B)对称轴是y轴
(C)都有最高点
(D)y随x的增大而增大
B
3.若点 在抛物线 上则
点A关于y轴对称点的坐标是( ).
(A)(2,4) (B)(-2,4)
(C)(2,-4) (D)(-2,-4)
B
巩固练习
对自己说,你有什么收获
对同学说,你有什么温馨提示
教科书习题 22.1 第 3,4 题.
5.布置作业
结束寄语
只有不断地思考,才会有新的发现;只有量的变化,才会有质的进步.
下课了!
22.1.2二次函数y=ax2的图象和性质
(第一课时)
九年级 上册
活动1 知识准备
1.一次函数的图象是一条________.
2.画函数图象的主要步骤是________、________、 ________.
3.点(-2,4)关于y轴对称的点的坐标是________.
4. 二次函数的一般形: ____,当一次项 ,常数项都是0时,二次函数的解析式_________。
直线
列表
描点
连线
(2,4)
数形结合,直观感受
观察y=x2,选择适当的x值,并计算相应的y值,完成下表:
用描点法画二次函数y=x2的图象
x
y=x2
x … -3 -2 -1 0 1 2 3 …
y=x2
x
y=x2 … 9 4 1 0 1 4 9 …
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
(2)描点:
(3)用光滑曲线顺次连接各点,便得到函数y= x2 的图象.
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴与抛物
线的交点叫做
抛物线的顶点.
在平面直角坐标系中描点,然后用光滑的曲线顺次连接各点,便得到了二次函数的图象,我们把这样的图象叫做________,抛物线有一条对称轴,对称轴与抛物线的交点叫做抛物线的________.
抛 物 线
顶 点
22.1.2 二次函数y=ax 的图象和性质
2
(1)抛物线的开口向________(填“下”或“上”)
(2)图象是中心对称图形还是轴对称图形?____________;
(3)当x<0时,曲线自左向右________(填“下降”或“上升”), 即y值随x值的增大而________(填“增大”或“减小”);
上
轴对称图形
下降
减小
(4)当x>0时,曲线自左向右________(填“下降”或“上升”),即y值随x值的增大而________(填“增大”或“减小”);
(5)图象在x轴的________(填“上方”或“下方”);
(6)顶点是抛物线上位置最________(填“高”或“低”)的点,y有最________(填“大”或“小”)值.
上升
增大
上方
低
小
x … -4 -3 -2 -1 0 1 2 3 4 …
y= x2
例1.在同一直角坐标系中画出函数y= x2 和 y=2x2的图像
解:(1)列表
(2)描点
(3)连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
1
2
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=2x2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
1
2
共同点:
不同点:
开口向上,顶点是原点,顶点是抛物线的最低点,对称轴是y轴,
除顶点外,图像都在x轴上方
开口大小不同
函数y= x2,y=2x2的图像与函数y=x2的图像相比,有什么共同点和不同点
1
2
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y=x2
y= 2x2
y= 0.5x2
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
在同一直角坐标系中画出函数y=- x2和y=-2x2的图像
1
2
y=- x2
1
2
y=-2x2
x
…
-4
-3
-2
-1
0
1
2
3
4
…
y=- x2
…
…
0
-2
-2
-8
-8
x
…
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
…
y=-2x2
…
…
0
-2
-2
-8
-8
函数y=- x2,y=-2x2的图像与y=-x2的图像相比,有什么共同点和不同点
1
2
共同点:
不同点:
开口向下,顶点是原点,对称轴是y轴,顶点是抛物线的最高点
除顶点外,图像都在x轴下方
开口大小不同
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
y=- x2
1
2
y=-2x2
y=-x2
A的取值
顶点坐标
对称轴
位置
开口方向
增减性
最值
a>0
a<0
(0,0)
(0,0)
Y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,y有最小值为0.
当x=0时, y有最大值为0.
当x<0时,y随着x的增大而减小.
在当x>0时, y随着x的增大而增大.
当x<0时,y随着x的增大而增大.
在x>0时, y随着x的增大而减小.
二次函数y=ax2的性质
︱a︱的越大,开口越小。
开口大小
说出下列抛物线的开口方向、对称轴和顶点:
(1) ;
(2) ;
(3) ;
(4) .
1.巩固练习
开口向上、y 轴、原点.
开口向下、y 轴、原点.
开口向上、y 轴、原点.
开口向下、y 轴、原点.
2.在同一坐标系中,图象与 的图象
关于 轴对称的函数为( ).
(A)
(B)
(C)
(D)
C
巩固练习
巩固练习
2.抛物线
共有的性质是( ).
(A)开口向上
(B)对称轴是y轴
(C)都有最高点
(D)y随x的增大而增大
B
3.若点 在抛物线 上则
点A关于y轴对称点的坐标是( ).
(A)(2,4) (B)(-2,4)
(C)(2,-4) (D)(-2,-4)
B
巩固练习
对自己说,你有什么收获
对同学说,你有什么温馨提示
教科书习题 22.1 第 3,4 题.
5.布置作业
结束寄语
只有不断地思考,才会有新的发现;只有量的变化,才会有质的进步.
下课了!
同课章节目录
