12.1 全等三角形课件
图片预览



文档简介
(共24张PPT)
探索三角形
全等的条件(1)
2 019
回顾知识
01.全等三角形的概念
02.全等三角形的性质
A
B
C
D
E
F
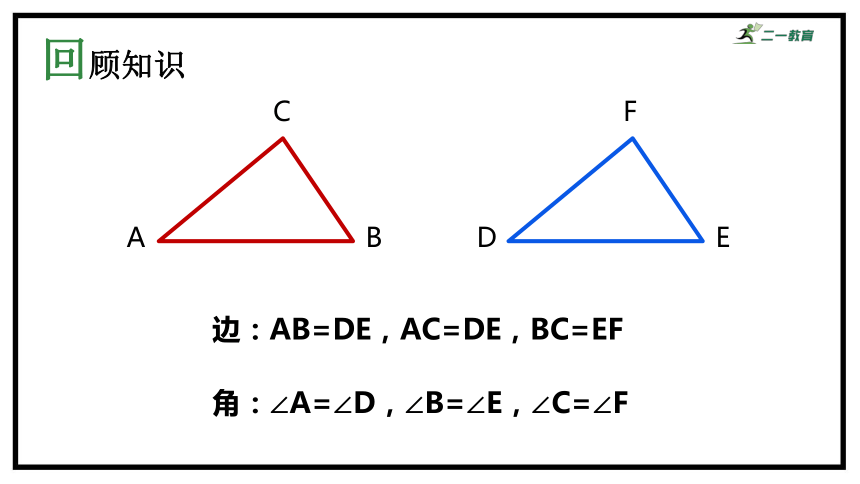
回顾知识
A
B
C
D
E
F
边:AB=DE,AC=DE,BC=EF
角:∠A=∠D,∠B=∠E,∠C=∠F
想一想
为班级文化建设,装饰教室,现在需要每人做一面三角形的彩旗,你需要知道几个与边或角有关的条件才能做出一个和它全等的彩旗呢?
②掌握利用“边边边”作为条件判定三角形全等的方法,能进行简单推理。
①经历探索三角形全等条件的过程,体会利用操作、归纳、获得数学结论的过程;
学习目标
③了解三角形的稳定性及其在生活中的应用。
想一想
为班级文化建设,装饰教室,现在需要每人做一面三角形的彩旗,你需要知道几个与边或角有关的条件才能做出一个和它全等的彩旗呢?
探索新知
探索新知
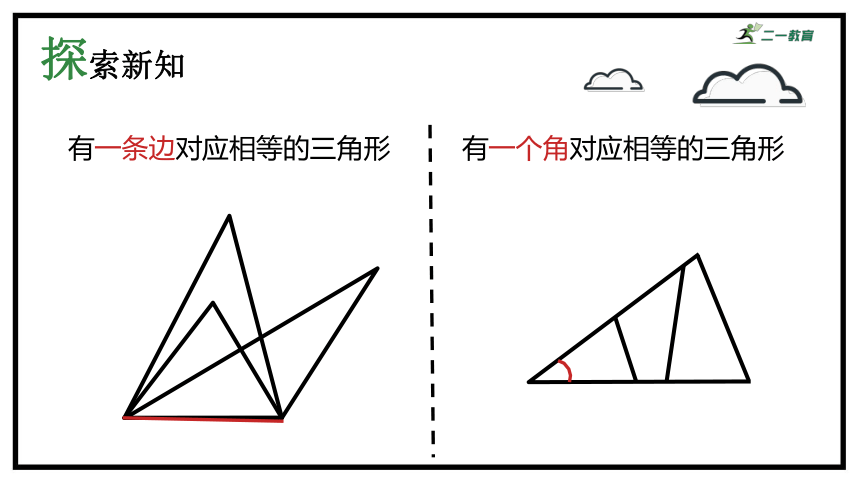
有一条边对应相等的三角形
有一个角对应相等的三角形
探索新知
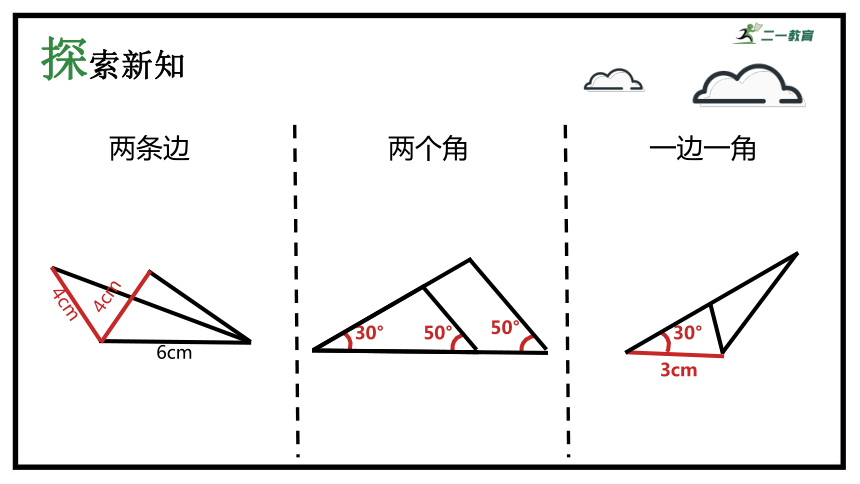
两条边
两个角
50°
30°
6cm
4cm
4cm
50°
一边一角
30°
3cm
探索新知
1、三个角
60°
90°
30°
60°
90°
不一定全等
不一定全等
探索新知
2、三条边
小 游 戏 —— 拼三角形
探索新知
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
A
B
C
A'
B'
C'
2、三条边
探索新知
A
B
C
用符号语言表示:
A'
B'
C'
在△ABC和△A'B'C'中
AC=A'C'
AB=A'B'
BC=B'C'
∴△ABC≌△A'B'C'(SSS)
例题解析
A
B
C
D
如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
归 纳
①写出在哪两个三角形中
②摆出三个条件用大括号括起来
③写出全等结论
三角形全等书写三步骤:
课堂练习
A
B
C
D
如图,AB=CD,AD=BC,则∠A与∠C相等吗?为什么?
A
B
C
D
课堂练习
A
B
C
D
E
如图,已知AB=AC,AE=AD,BD=CE,试说明△ABE≌△ACD.
解: BD=CE(已知)
BD-ED=CE-ED(等式的基本性质)
即BE=CD.
在△ABE和△ACD中,
AB=AC(已知)
AE=AD(已知)
BE=CD(已证)
△ABE≌△ACD(SSS)
练一练
如图,AB=CD,BF=DE,E,F是AC上两点,且AE=CF.请你判断BF与DE的位置关系,并说明理由.
取出三根硬纸条钉成一个三角形,你能拉动其中两边,使这个三角形的形状发生变化吗?
取出四根硬纸条钉成一个四边形,拉动其中两边,这个四边形的形状改变了吗?钉成 一个五边形,又会怎么样?
上面的现象说明了什么?
三角形具有稳定性
三角形具有稳定性
课堂小结
(4)题目中“边”相等这个条件的给出(直接、间接)
(1)只给出一个条件或两个条件时,都不能保证两个三角形全等.
(2)三个内角对应相等的两个三角形不一 定全等.
(3)边边边公理:三边对应相等的两个三角形全等,简写为“边边
边”或“SSS”.
(5)三角形具有稳定性。
2 019
谢谢!
探索三角形
全等的条件(1)
2 019
回顾知识
01.全等三角形的概念
02.全等三角形的性质
A
B
C
D
E
F
回顾知识
A
B
C
D
E
F
边:AB=DE,AC=DE,BC=EF
角:∠A=∠D,∠B=∠E,∠C=∠F
想一想
为班级文化建设,装饰教室,现在需要每人做一面三角形的彩旗,你需要知道几个与边或角有关的条件才能做出一个和它全等的彩旗呢?
②掌握利用“边边边”作为条件判定三角形全等的方法,能进行简单推理。
①经历探索三角形全等条件的过程,体会利用操作、归纳、获得数学结论的过程;
学习目标
③了解三角形的稳定性及其在生活中的应用。
想一想
为班级文化建设,装饰教室,现在需要每人做一面三角形的彩旗,你需要知道几个与边或角有关的条件才能做出一个和它全等的彩旗呢?
探索新知
探索新知
有一条边对应相等的三角形
有一个角对应相等的三角形
探索新知
两条边
两个角
50°
30°
6cm
4cm
4cm
50°
一边一角
30°
3cm
探索新知
1、三个角
60°
90°
30°
60°
90°
不一定全等
不一定全等
探索新知
2、三条边
小 游 戏 —— 拼三角形
探索新知
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
A
B
C
A'
B'
C'
2、三条边
探索新知
A
B
C
用符号语言表示:
A'
B'
C'
在△ABC和△A'B'C'中
AC=A'C'
AB=A'B'
BC=B'C'
∴△ABC≌△A'B'C'(SSS)
例题解析
A
B
C
D
如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
归 纳
①写出在哪两个三角形中
②摆出三个条件用大括号括起来
③写出全等结论
三角形全等书写三步骤:
课堂练习
A
B
C
D
如图,AB=CD,AD=BC,则∠A与∠C相等吗?为什么?
A
B
C
D
课堂练习
A
B
C
D
E
如图,已知AB=AC,AE=AD,BD=CE,试说明△ABE≌△ACD.
解: BD=CE(已知)
BD-ED=CE-ED(等式的基本性质)
即BE=CD.
在△ABE和△ACD中,
AB=AC(已知)
AE=AD(已知)
BE=CD(已证)
△ABE≌△ACD(SSS)
练一练
如图,AB=CD,BF=DE,E,F是AC上两点,且AE=CF.请你判断BF与DE的位置关系,并说明理由.
取出三根硬纸条钉成一个三角形,你能拉动其中两边,使这个三角形的形状发生变化吗?
取出四根硬纸条钉成一个四边形,拉动其中两边,这个四边形的形状改变了吗?钉成 一个五边形,又会怎么样?
上面的现象说明了什么?
三角形具有稳定性
三角形具有稳定性
课堂小结
(4)题目中“边”相等这个条件的给出(直接、间接)
(1)只给出一个条件或两个条件时,都不能保证两个三角形全等.
(2)三个内角对应相等的两个三角形不一 定全等.
(3)边边边公理:三边对应相等的两个三角形全等,简写为“边边
边”或“SSS”.
(5)三角形具有稳定性。
2 019
谢谢!
