湘教版数学八年级下册 说课课件:2.4《三角形的中位线》(共20张PPT)
文档属性
| 名称 | 湘教版数学八年级下册 说课课件:2.4《三角形的中位线》(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 549.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-26 00:00:00 | ||
图片预览






文档简介
课件20张PPT。 三角形的中位线1、教材的地位和作用2、教材的重点、难点[重点]探索三角形中位线性质的过程,体会转化思想 [难点]利用中心对称性质研究得到三角形中位线的性质。 本节教材是在学生学地了三角形,平行四边形内容之后作为
三角形和四边形知识的应用和深化,是三角形的一个重要性质定
理,在证明两直线平行和论证线段倍分关系时常常要用到,它起
到承上启下的作用。通过学习,使学生再次体会数学来源于生活,
提高学生学习数的兴趣,都是极其重要的。1、知识技能:2、过程方法:3、情感态度与价值观:(1)了解三角形中位线的概念,探索并掌握三角形中位线的性质。
(2)能应用三角形中位线的性质解决有关的推理与计算问题。经历探索三角形中位线性质的过程,体会转化的思想方法,进一
步发展学生操作、观察、归纳、推理能力;让学生接触并解决一些
现实生活中的问题逐步培养学生的应用能力和创新意识。通过真实的、贴近学生生活的素材和适当的问题情境,激发学生学
习数学的热情和兴趣;通过对三角形中位线的研究,体验数学活动
充满探索性和创造性,在操作活动中,培养学生的合作精神。 教法: “启发、探究”
通过设置情境、操作实验、猜想论证等数学活动过程,让学生主动参与到知识的建构过程中去,充分发挥学生的主体作用,教学中突出数学思想的指导作用,以有效化解教学难点。
学法: “自主探索、合作交流”
利用学生的好奇心设疑、解疑,让学生在动手实践、自主探索与合作交流的中主动获取知识,这样做,不仅切合学生的实际、符合学生的认知规律,而且注重了学生思维的发展和能力的培养,真正做到以学生为学习的主体.
创设情境 建模 探究、应用、拓展数学化:
构建立中位线概念、
探索中位线定理数学现实:
贴近生活的实际背景 再创造:
中位线定理的证明
及其应用创设情境 导入新课回顾定义引出新知
实践探索感受特征课后作业巩固加深发散练习拓展提高回顾小结整体感知
(一)创设情境 导入新课1、你见过如图1的木制屋顶架吗? 图1 MN为横梁,它上面A、B间距离是确定的,等于房子宽度,根据它的长度和相应的规定,确定了斜梁PA(PB)与竖梁PQ的长度,为了防止斜梁被屋顶上所盖瓦的重量压垮,还要在它的中点C(E)安上支柱CD(EF),那么CD(EF)的长度与PQ的长度有什么关系呢?为什么?P2、如图2,E、F分别是AB、AC的中点,
那么EF与BC在数量和位置上各有什么关系?为解决这类问题,本节课我们一起来共同探究:三角形的中位线 图21、三角形的中线的定义:2、三角形的中位线的定义:(二)回顾定义,引出新知三角形的中位线有什么性质?如图,EF是△ABC的一条中位线.量一量EF,BC的长是多少?你能作出什么猜测?ABCEF你能从图中猜测EF ∥BC 吗?三角形的中位线等于第三边的一半EF ∥BC上述这些猜测正确吗?(三)实践探索,感受特征设点F的像点是点H,由于F是AC的中点,因此H是BD的中点. 连结AD,DB,由于EA=EB,ED=EC,因此四边形ADBC是平行四边形,(对角线互相平分的四边形是平行四边形)把△ABC绕点E旋转180°,则点A的像点是点B,点B的像点是点A,点C的像点是D,从而线段AC的像是线段BD.ABCFHDE 因此四边形FHBC是平行四边形(一组对边平行且相等的四边形是平行四边形)从而HF∥BC,HF=BC,由于EF=EH,因此从而AC∥DB,AC=DB,于是FC∥HB,且三角形的中位线平行于第三边,并且等于第三边的一半.例3:如图,顺次连结四边形ABCD各边中点E,F,H,M,得到的四边形EFHM是平行四边形吗?为什么?连结AC于是EF∥MH,且EF=MH所以四边形EFHM是平行四边形.解ABCDEFHM由于EF是△ABC的一条中位线,因此EF∥AC,且由于MH是△DAC的一条中位线,因此MH∥AC,且1.在例3中,设四边形ABCD的两条对角线AC,BD的长分别为5cm,4.4cm,E,F,H,M分别是边AB,BC,CD,DA的中点,求四边形 EFHM的周长.解:根据三角形中位线定理:∴平行 四边形MEFH的周长是(四)发散练习,拓展提高2. 已知△ABC的各边长长度分别为3cm,3.4cm,4cm,求连结各边中点所成△DEF的周长.△DEF的周长=DE+DF+EF解:答: △DEF的周长是5.2(cm)3.如图,△ABC的边BC,CA,AB的中点分别是D,E,F
(1)四边形AFDE是平行四边形吗?为什么?
(2)四边形AFDE的周长等于AB+AC吗?为什么?ABCEFD(1) 四边形AFDE是平行四边形∵ DE和DF是△ABC的中位线∴ DE∥AB DF∥AC∴四边形AFDE是平行四边形(2) AFDE的周长等于AB+AC四边形AFDE的周长本课小结 1.理解三角形中位线的概念:连接三角形两边中点的线段叫做三角形的中位线。
2.掌握三角形中位线的性质:三角形的中位线平行于第三边,并且等于它的一半。
3.能应用三角形中位线的性质解决有关计算或说理等问题。(五)回顾小结,整体感知检 测1.已知三角形的3条中位线分别是3 ,4 ,6 ,则这个三角
形的周长是 2.如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N 是边AB 的中点,问△MPN 是什么三角形?为什么?26解:是等腰三角形理由如下:∵点P与点M分别是BD与DC中点∴PM是△BCD的中位线∴PM= BC(六)课后作业,巩固加深3.已知,如图 ,在三角形ABC中,AE=EC,
AD⊥BC,EF ⊥BC,BE=2EF,问AD与BE相等吗?为什么?4.如图,在△ABC中,点D在BC上,且CD=AC,CE⊥AD
垂足为E,点F是AB的中点。
求证:EF∥BC
三角形和四边形知识的应用和深化,是三角形的一个重要性质定
理,在证明两直线平行和论证线段倍分关系时常常要用到,它起
到承上启下的作用。通过学习,使学生再次体会数学来源于生活,
提高学生学习数的兴趣,都是极其重要的。1、知识技能:2、过程方法:3、情感态度与价值观:(1)了解三角形中位线的概念,探索并掌握三角形中位线的性质。
(2)能应用三角形中位线的性质解决有关的推理与计算问题。经历探索三角形中位线性质的过程,体会转化的思想方法,进一
步发展学生操作、观察、归纳、推理能力;让学生接触并解决一些
现实生活中的问题逐步培养学生的应用能力和创新意识。通过真实的、贴近学生生活的素材和适当的问题情境,激发学生学
习数学的热情和兴趣;通过对三角形中位线的研究,体验数学活动
充满探索性和创造性,在操作活动中,培养学生的合作精神。 教法: “启发、探究”
通过设置情境、操作实验、猜想论证等数学活动过程,让学生主动参与到知识的建构过程中去,充分发挥学生的主体作用,教学中突出数学思想的指导作用,以有效化解教学难点。
学法: “自主探索、合作交流”
利用学生的好奇心设疑、解疑,让学生在动手实践、自主探索与合作交流的中主动获取知识,这样做,不仅切合学生的实际、符合学生的认知规律,而且注重了学生思维的发展和能力的培养,真正做到以学生为学习的主体.
创设情境 建模 探究、应用、拓展数学化:
构建立中位线概念、
探索中位线定理数学现实:
贴近生活的实际背景 再创造:
中位线定理的证明
及其应用创设情境 导入新课回顾定义引出新知
实践探索感受特征课后作业巩固加深发散练习拓展提高回顾小结整体感知
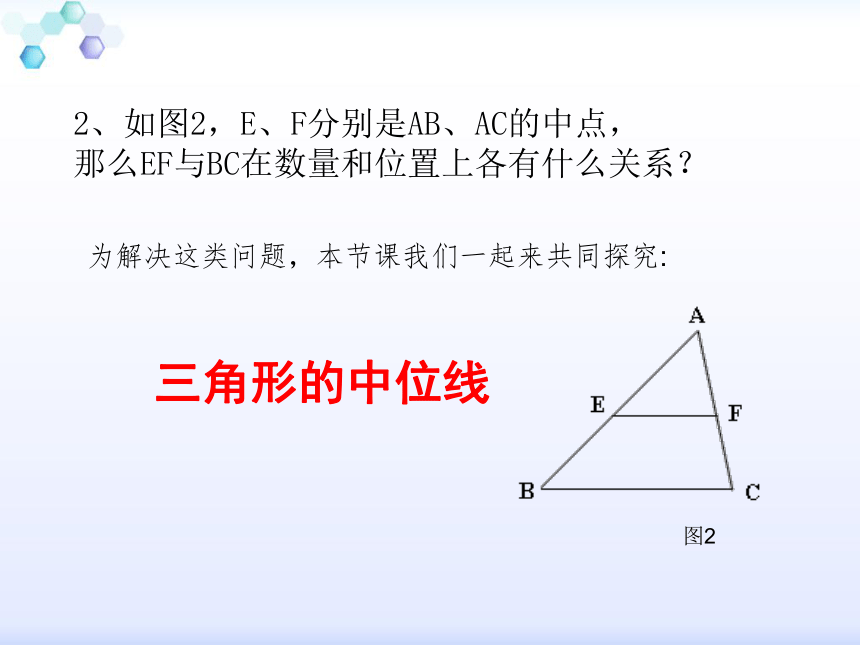
(一)创设情境 导入新课1、你见过如图1的木制屋顶架吗? 图1 MN为横梁,它上面A、B间距离是确定的,等于房子宽度,根据它的长度和相应的规定,确定了斜梁PA(PB)与竖梁PQ的长度,为了防止斜梁被屋顶上所盖瓦的重量压垮,还要在它的中点C(E)安上支柱CD(EF),那么CD(EF)的长度与PQ的长度有什么关系呢?为什么?P2、如图2,E、F分别是AB、AC的中点,
那么EF与BC在数量和位置上各有什么关系?为解决这类问题,本节课我们一起来共同探究:三角形的中位线 图21、三角形的中线的定义:2、三角形的中位线的定义:(二)回顾定义,引出新知三角形的中位线有什么性质?如图,EF是△ABC的一条中位线.量一量EF,BC的长是多少?你能作出什么猜测?ABCEF你能从图中猜测EF ∥BC 吗?三角形的中位线等于第三边的一半EF ∥BC上述这些猜测正确吗?(三)实践探索,感受特征设点F的像点是点H,由于F是AC的中点,因此H是BD的中点. 连结AD,DB,由于EA=EB,ED=EC,因此四边形ADBC是平行四边形,(对角线互相平分的四边形是平行四边形)把△ABC绕点E旋转180°,则点A的像点是点B,点B的像点是点A,点C的像点是D,从而线段AC的像是线段BD.ABCFHDE 因此四边形FHBC是平行四边形(一组对边平行且相等的四边形是平行四边形)从而HF∥BC,HF=BC,由于EF=EH,因此从而AC∥DB,AC=DB,于是FC∥HB,且三角形的中位线平行于第三边,并且等于第三边的一半.例3:如图,顺次连结四边形ABCD各边中点E,F,H,M,得到的四边形EFHM是平行四边形吗?为什么?连结AC于是EF∥MH,且EF=MH所以四边形EFHM是平行四边形.解ABCDEFHM由于EF是△ABC的一条中位线,因此EF∥AC,且由于MH是△DAC的一条中位线,因此MH∥AC,且1.在例3中,设四边形ABCD的两条对角线AC,BD的长分别为5cm,4.4cm,E,F,H,M分别是边AB,BC,CD,DA的中点,求四边形 EFHM的周长.解:根据三角形中位线定理:∴平行 四边形MEFH的周长是(四)发散练习,拓展提高2. 已知△ABC的各边长长度分别为3cm,3.4cm,4cm,求连结各边中点所成△DEF的周长.△DEF的周长=DE+DF+EF解:答: △DEF的周长是5.2(cm)3.如图,△ABC的边BC,CA,AB的中点分别是D,E,F
(1)四边形AFDE是平行四边形吗?为什么?
(2)四边形AFDE的周长等于AB+AC吗?为什么?ABCEFD(1) 四边形AFDE是平行四边形∵ DE和DF是△ABC的中位线∴ DE∥AB DF∥AC∴四边形AFDE是平行四边形(2) AFDE的周长等于AB+AC四边形AFDE的周长本课小结 1.理解三角形中位线的概念:连接三角形两边中点的线段叫做三角形的中位线。
2.掌握三角形中位线的性质:三角形的中位线平行于第三边,并且等于它的一半。
3.能应用三角形中位线的性质解决有关计算或说理等问题。(五)回顾小结,整体感知检 测1.已知三角形的3条中位线分别是3 ,4 ,6 ,则这个三角
形的周长是 2.如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N 是边AB 的中点,问△MPN 是什么三角形?为什么?26解:是等腰三角形理由如下:∵点P与点M分别是BD与DC中点∴PM是△BCD的中位线∴PM= BC(六)课后作业,巩固加深3.已知,如图 ,在三角形ABC中,AE=EC,
AD⊥BC,EF ⊥BC,BE=2EF,问AD与BE相等吗?为什么?4.如图,在△ABC中,点D在BC上,且CD=AC,CE⊥AD
垂足为E,点F是AB的中点。
求证:EF∥BC
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
