1.3.1正方形的性质课件(35张PPT) 2023-2024学年北师大版九年级数学上册
文档属性
| 名称 | 1.3.1正方形的性质课件(35张PPT) 2023-2024学年北师大版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-13 14:34:20 | ||
图片预览


文档简介
(共35张PPT)
1.3 正方形的性质与判定
第1课时 正方形的性质
第一章 特殊的平行四边形
创设情境,导入新课
生活中的正方形
好
好
学
习
天
天
向
上
像矩形
十
年
树
木
百
年
树
人
像菱形
矩形
前面我们已经学过了,平行四边形,矩形,菱形,想一想,矩形是由什么图形怎样变化而来?
平行四边形
菱形
邻边相等
菱形是由什么图形怎样变化而来?
问题1:矩形怎样变化后就成了正方形呢
你有什么发现?
正方形的性质
1
矩 形
〃
〃
正方形
一组邻边相等
问题2:菱形怎样变化后就成了正方形呢
你有什么发现?
正方形
一个角是90°
探究新知,经历过程
图中的四边形都是特殊的平行四边形. 观察这些特殊的平行四边形,你能发现它们有什么样的共同特征?
你能总结出正方形的定义吗?
正方形定义:
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
(1)正方形是矩形吗?是菱形吗?
(2)你认为正方形具有哪些性质?与同伴交流.
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.它具有矩形与菱形以及平行四边形的所有性质.
总结
议一议
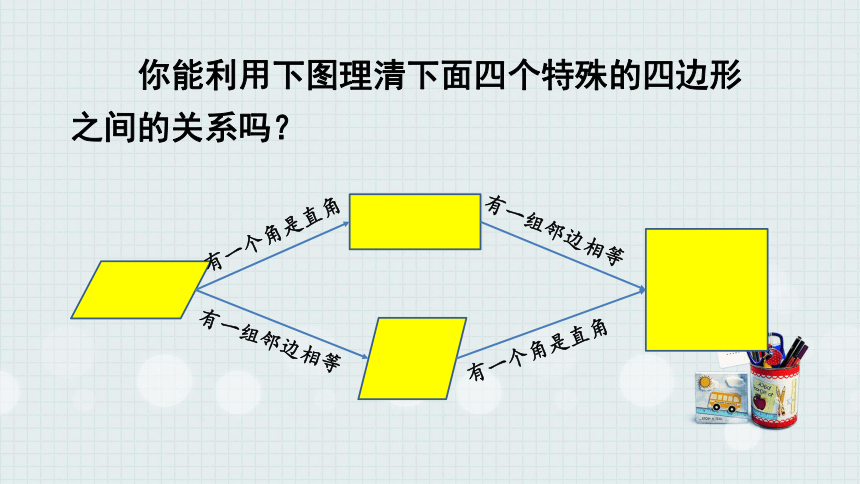
你能利用下图理清下面四个特殊的四边形之间的关系吗?
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
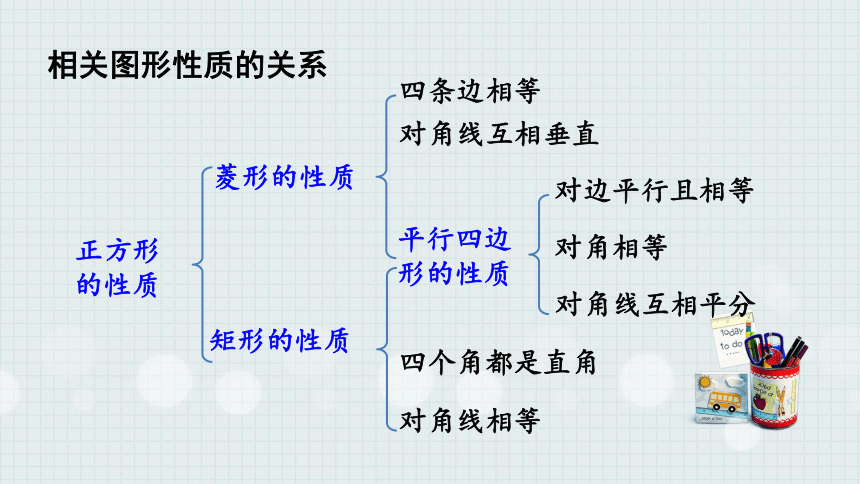
相关图形性质的关系
平行四边形的性质
对边平行且相等
对角相等
对角线互相平分
菱形的性质
四条边相等
对角线互相垂直
四个角都是直角
对角线相等
矩形的性质
正方形的性质
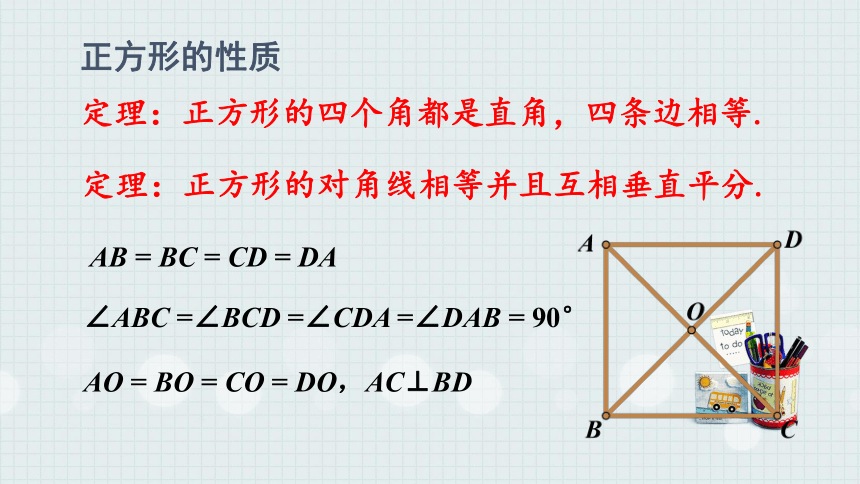
正方形的性质
定理:正方形的四个角都是直角,四条边相等.
定理:正方形的对角线相等并且互相垂直平分.
AB = BC = CD = DA
∠ABC =∠BCD =∠CDA =∠DAB = 90°
AO = BO = CO = DO,AC⊥BD
证明:∵ 四边形 ABCD 是正方形.
∴∠A = 90°,AB = AD (正方形的定义).
又∵ 正方形是平行四边形,
∴ 正方形是矩形 (矩形的定义),
正方形是菱形 (菱形的定义).
∴∠A =∠B =∠C =∠D = 90°,
AB = BC = CD = AD.
(1) 已知:如图,四边形 ABCD 是正方形.
求证:正方形 ABCD 四边相等,四个角都是直角.
A
B
C
D
证一证
(2) 已知:如图,四边形 ABCD 是正方形. 对角线 AC、BD 相交于点 O. 求证:AO = BO = CO = DO,AC⊥BD.
A
B
C
D
O
证明:∵ 正方形 ABCD 是矩形,
∴ AO = BO = CO = DO.
∵ 正方形 ABCD 是菱形,
∴ AC⊥BD.
平行四边形、矩形、菱形、正方形之间的关系:
四边形
平行四边形
菱形
矩形
正方形
韦恩图:
归纳总结
定理 正方形的四个角都是直角,四条边相等.
定理 正方形的对角线相等且互相垂直平分.
正方形的性质
根据图形所具有的性质,在下表相应的空格中打“√”.
判一判
性质\图形 平行四边形 矩形 菱形 正方形
边 对边平行且相等
四边相等
角 四个角都是直角
对角线 对角线相互平分
对角线相互垂直
对角线相等
每条对角线平分一组对角
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
想一想
正方形是不是轴对称图形?
如果是,那么对称轴有几条?
正方形既是轴对称图形,又是中心对称图形.
对称性: ,
对称轴: .
轴对称图形
4 条
例1 如图,在正方形 ABCD 中,E 为 CD 上一点,F 为 BC 边延长线上一点,且 CE = CF. BE 与 DF 之间有怎样的关系?请说明理由.
解:BE = DF,且 BE⊥DF. 理由如下:
①∵ 四边形 ABCD 是正方形.
∴ BC = DC,∠BCE = 90°,
∴∠DCF = 180° -∠BCE =180° - 90° = 90°.
∴∠BCE =∠DCF.
又∵ CE = CF,
A
B
D
C
F
E
∴ △BCE≌△DCF (SAS).
∴ BE = DF.
A
B
D
F
E
② 延长 BE 交 DF 于点 M.
∵△BCE≌△DCF,
∴∠CBE =∠CDF.
∵∠DCF = 90°,
∴∠CDF +∠F = 90°.
∴∠CBE +∠F = 90°.
∴∠BMF = 90°,∴ BE⊥DF.
综和①②可知,BE = DF,且 BE⊥DF.
C
M
例2 如图,在正方形 ABCD 中,△BEC 是等边三角形,
求证: ∠EAD =∠EDA = 15°.
证明:∵ △BEC 是等边三角形,
∴ BE = CE = BC,∠EBC =∠ECB = 60°.
∵ 四边形 ABCD 是正方形,
∴ AB = BC = CD,∠ABC =∠DCB = 90°.
∴ AB = BE = CE = CD, ∠ABE =∠DCE = 30°.
∴△ABE,△DCE 是等腰三角形.
∴∠BAE =∠BEA =∠CDE =∠CED = 75°.
∴∠EAD =∠EDA = 90°-75° = 15°.
四边形 ABCD 是正方形,以正方形 ABCD 的一边为边作等边△ADE,求∠BEC 的大小.(分类讨论)
解:当点 E 在正方形 ABCD 外部时,如图①,AB=AE,∠BAE=90°+60°=150°.
∴∠AEB=15°.
同理可得∠DEC=15°.
∴∠BEC=60°-15°-15°=30°;
【变式题1】
当点 E 在正方形 ABCD 内部时,如图②,
AB=AE,∠BAE=90°-60°=30°,
∴∠AEB=75°.
同理可得∠DEC=75°.
∴∠BEC=360°-75°-75°-60°=150°.
综上所述,∠BEC 的大小为 30° 或 150°.
易错提醒:因为等边△ADE 与正方形 ABCD 有一条公共边,所以它们的边相等.本题分点 E 在正方形的外部和在正方形的内部两种情况.
【变式题2】 如图,在正方形 ABCD 内有一点 P 满足 AP = AB,PB = PC,连接 AC、PD.
(1)求证:△APB≌△DPC;
证明:∵ 四边形 ABCD 是正方形,
∴∠ABC =∠DCB = 90°.
∵ PB = PC,
∴∠PBC =∠PCB.
∴∠ABC -∠PBC =∠DCB -∠PCB,
即∠ABP =∠DCP.
又∵ AB = DC,PB = PC,
∴△APB≌△DPC.
证明:∵ 四边形 ABCD 是正方形,
∴∠BAC =∠DAC = 45°.
∵△APB≌△DPC,∴ AP = DP.
又∵AP = AB = AD,
∴ DP = AP = AD,
即 △APD 是等边三角形.
∴∠DAP = 60°.
∴∠PAC =∠DAP -∠DAC = 15°,
∠BAP =∠DAB -∠DAP = 30°.
∴∠BAP = 2∠PAC.
(2)求证:∠BAP = 2∠PAC.
2. 一个正方形的对角线长为 2 cm,则它的面积是( )
A. 2 cm2 B. 4 cm2 C. 6 cm2 D. 8 cm2
A
1. 平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
A
3. 在正方形 ABCD 中,∠ADB = °,∠DAC = °, ∠BOC = °.
4. 在正方形 ABCD 中,E 是对角线 AC 上一点,且 AE = AB,则∠EBC 的度数是 .
A
D
B
C
O
A
D
B
C
O
E
45
90
22.5°
第3题图
第4题图
45
1. 四个角都是直角
2. 四条边都相等
3. 对角线相等且互相垂直平分
正方形的性质
性质
定义
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
如图,在正方形 ABCD 中,对角线 AC 与 BD 相交于点 O,图中有多少个等腰三角形?它们分别是?(列出来)
【选自教材P21 随堂练习】
巩固练习,深化提高
解:图中共有 8 个等腰三角形.
△OAB、△OBC、△OCD、△ODA、△ABC、△BCD、△CDA、△DAB
2. 如图,在正方形 ABCD 中,点 F 为对角线 AC 上一点,
连接 BF, DF。你能找出图中的全等三角形吗?选择其
中一对进行证明.
解:图中的全等三角形共有 3 对,
分别是 △ADC 与 △ABC(SAS),
△FCD与 △FCB(SAS),
△FAD 与 △FAB(SAS).
【选自教材P21 随堂练习】
2. 如图,在正方形 ABCD 中,点 F 为对角线 AC 上一点,
连接 BF, DF。你能找出图中的全等三角形吗?选择其
中一对进行证明.
选择△FAD≌△FAB 证明,过程如下:
∵正方形 ABCD,
∴AD = AB,∠DAF =∠BAF,
又∵AF = AF,
∴△FAD≌△FAB.
【选自教材P21 随堂练习】
【选自教材P22 习题1.7 第1题】
3. 对角线长为 2 cm 的正方形,边长是多少?
解:∵ABCD 是正方形,
∴AB = BC,∠B = 90°
△ABC是等腰直角三角形,
AB2 + BC2 = AC2 = 4,
∴AB =
【选自教材P22 习题1.7 第2题】
4. 如图,四边形 ABCD 是正方形,△CBE 是等边三角形,
求∠AEB 的度数.
证明: ∵△BEC 是等边三角形,
∴BE = EC = BC = AB,
∴△ABE 是等腰三角形,
∴ ∠ABE = 90°-60° = 30 °
∴∠AEB = = 75 °
【选自教材P22 习题1.7 第3题】
5. 如图,A,B,C,D 四家工厂分别坐落在正方形城镇的四
个角上.仓库 P 和 Q 分别位于 AD 和 DC 上,且 PD = QC.
证明两条直路 BP = AQ 且 BP⊥AQ.
证明: 如图, AQ 与 BP 交于点 O.
在正方形 ABCD 中,
∵PD = QC, ∴DQ = AP .
又∵AB = AD ,∠D =∠PAB = 90°,
∴△ABP ≌△DAQ(SAS).
∴BP =AQ,∠DAQ=∠ABP .
∵∠ABP +∠APB= 90°=∠DAQ+∠APB.
∴∠AOP =90°.∴BP =AQ 且 BP ⊥ AQ.
6. 在一个正方形的花坛上,欲修建两条直的小路,使得两条
直的小路将花坛分成大小、形状完全相同的四部分(不考
虑道路的宽度).你有几种方法?画出图
【选自教材P22 习题1.7 第4题】
课堂小结
这节课你们都学会了哪些知识?
正方形的定义
正方形的性质
正方形的对角线相等并且互相垂直平分.
有一组邻边相等,并且有一个角是直角的平行四边形,叫做正方形.
正方形的四个角都是直角,四条边相等.
1.3 正方形的性质与判定
第1课时 正方形的性质
第一章 特殊的平行四边形
创设情境,导入新课
生活中的正方形
好
好
学
习
天
天
向
上
像矩形
十
年
树
木
百
年
树
人
像菱形
矩形
前面我们已经学过了,平行四边形,矩形,菱形,想一想,矩形是由什么图形怎样变化而来?
平行四边形
菱形
邻边相等
菱形是由什么图形怎样变化而来?
问题1:矩形怎样变化后就成了正方形呢
你有什么发现?
正方形的性质
1
矩 形
〃
〃
正方形
一组邻边相等
问题2:菱形怎样变化后就成了正方形呢
你有什么发现?
正方形
一个角是90°
探究新知,经历过程
图中的四边形都是特殊的平行四边形. 观察这些特殊的平行四边形,你能发现它们有什么样的共同特征?
你能总结出正方形的定义吗?
正方形定义:
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
(1)正方形是矩形吗?是菱形吗?
(2)你认为正方形具有哪些性质?与同伴交流.
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.它具有矩形与菱形以及平行四边形的所有性质.
总结
议一议
你能利用下图理清下面四个特殊的四边形之间的关系吗?
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
相关图形性质的关系
平行四边形的性质
对边平行且相等
对角相等
对角线互相平分
菱形的性质
四条边相等
对角线互相垂直
四个角都是直角
对角线相等
矩形的性质
正方形的性质
正方形的性质
定理:正方形的四个角都是直角,四条边相等.
定理:正方形的对角线相等并且互相垂直平分.
AB = BC = CD = DA
∠ABC =∠BCD =∠CDA =∠DAB = 90°
AO = BO = CO = DO,AC⊥BD
证明:∵ 四边形 ABCD 是正方形.
∴∠A = 90°,AB = AD (正方形的定义).
又∵ 正方形是平行四边形,
∴ 正方形是矩形 (矩形的定义),
正方形是菱形 (菱形的定义).
∴∠A =∠B =∠C =∠D = 90°,
AB = BC = CD = AD.
(1) 已知:如图,四边形 ABCD 是正方形.
求证:正方形 ABCD 四边相等,四个角都是直角.
A
B
C
D
证一证
(2) 已知:如图,四边形 ABCD 是正方形. 对角线 AC、BD 相交于点 O. 求证:AO = BO = CO = DO,AC⊥BD.
A
B
C
D
O
证明:∵ 正方形 ABCD 是矩形,
∴ AO = BO = CO = DO.
∵ 正方形 ABCD 是菱形,
∴ AC⊥BD.
平行四边形、矩形、菱形、正方形之间的关系:
四边形
平行四边形
菱形
矩形
正方形
韦恩图:
归纳总结
定理 正方形的四个角都是直角,四条边相等.
定理 正方形的对角线相等且互相垂直平分.
正方形的性质
根据图形所具有的性质,在下表相应的空格中打“√”.
判一判
性质\图形 平行四边形 矩形 菱形 正方形
边 对边平行且相等
四边相等
角 四个角都是直角
对角线 对角线相互平分
对角线相互垂直
对角线相等
每条对角线平分一组对角
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
想一想
正方形是不是轴对称图形?
如果是,那么对称轴有几条?
正方形既是轴对称图形,又是中心对称图形.
对称性: ,
对称轴: .
轴对称图形
4 条
例1 如图,在正方形 ABCD 中,E 为 CD 上一点,F 为 BC 边延长线上一点,且 CE = CF. BE 与 DF 之间有怎样的关系?请说明理由.
解:BE = DF,且 BE⊥DF. 理由如下:
①∵ 四边形 ABCD 是正方形.
∴ BC = DC,∠BCE = 90°,
∴∠DCF = 180° -∠BCE =180° - 90° = 90°.
∴∠BCE =∠DCF.
又∵ CE = CF,
A
B
D
C
F
E
∴ △BCE≌△DCF (SAS).
∴ BE = DF.
A
B
D
F
E
② 延长 BE 交 DF 于点 M.
∵△BCE≌△DCF,
∴∠CBE =∠CDF.
∵∠DCF = 90°,
∴∠CDF +∠F = 90°.
∴∠CBE +∠F = 90°.
∴∠BMF = 90°,∴ BE⊥DF.
综和①②可知,BE = DF,且 BE⊥DF.
C
M
例2 如图,在正方形 ABCD 中,△BEC 是等边三角形,
求证: ∠EAD =∠EDA = 15°.
证明:∵ △BEC 是等边三角形,
∴ BE = CE = BC,∠EBC =∠ECB = 60°.
∵ 四边形 ABCD 是正方形,
∴ AB = BC = CD,∠ABC =∠DCB = 90°.
∴ AB = BE = CE = CD, ∠ABE =∠DCE = 30°.
∴△ABE,△DCE 是等腰三角形.
∴∠BAE =∠BEA =∠CDE =∠CED = 75°.
∴∠EAD =∠EDA = 90°-75° = 15°.
四边形 ABCD 是正方形,以正方形 ABCD 的一边为边作等边△ADE,求∠BEC 的大小.(分类讨论)
解:当点 E 在正方形 ABCD 外部时,如图①,AB=AE,∠BAE=90°+60°=150°.
∴∠AEB=15°.
同理可得∠DEC=15°.
∴∠BEC=60°-15°-15°=30°;
【变式题1】
当点 E 在正方形 ABCD 内部时,如图②,
AB=AE,∠BAE=90°-60°=30°,
∴∠AEB=75°.
同理可得∠DEC=75°.
∴∠BEC=360°-75°-75°-60°=150°.
综上所述,∠BEC 的大小为 30° 或 150°.
易错提醒:因为等边△ADE 与正方形 ABCD 有一条公共边,所以它们的边相等.本题分点 E 在正方形的外部和在正方形的内部两种情况.
【变式题2】 如图,在正方形 ABCD 内有一点 P 满足 AP = AB,PB = PC,连接 AC、PD.
(1)求证:△APB≌△DPC;
证明:∵ 四边形 ABCD 是正方形,
∴∠ABC =∠DCB = 90°.
∵ PB = PC,
∴∠PBC =∠PCB.
∴∠ABC -∠PBC =∠DCB -∠PCB,
即∠ABP =∠DCP.
又∵ AB = DC,PB = PC,
∴△APB≌△DPC.
证明:∵ 四边形 ABCD 是正方形,
∴∠BAC =∠DAC = 45°.
∵△APB≌△DPC,∴ AP = DP.
又∵AP = AB = AD,
∴ DP = AP = AD,
即 △APD 是等边三角形.
∴∠DAP = 60°.
∴∠PAC =∠DAP -∠DAC = 15°,
∠BAP =∠DAB -∠DAP = 30°.
∴∠BAP = 2∠PAC.
(2)求证:∠BAP = 2∠PAC.
2. 一个正方形的对角线长为 2 cm,则它的面积是( )
A. 2 cm2 B. 4 cm2 C. 6 cm2 D. 8 cm2
A
1. 平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
A
3. 在正方形 ABCD 中,∠ADB = °,∠DAC = °, ∠BOC = °.
4. 在正方形 ABCD 中,E 是对角线 AC 上一点,且 AE = AB,则∠EBC 的度数是 .
A
D
B
C
O
A
D
B
C
O
E
45
90
22.5°
第3题图
第4题图
45
1. 四个角都是直角
2. 四条边都相等
3. 对角线相等且互相垂直平分
正方形的性质
性质
定义
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
如图,在正方形 ABCD 中,对角线 AC 与 BD 相交于点 O,图中有多少个等腰三角形?它们分别是?(列出来)
【选自教材P21 随堂练习】
巩固练习,深化提高
解:图中共有 8 个等腰三角形.
△OAB、△OBC、△OCD、△ODA、△ABC、△BCD、△CDA、△DAB
2. 如图,在正方形 ABCD 中,点 F 为对角线 AC 上一点,
连接 BF, DF。你能找出图中的全等三角形吗?选择其
中一对进行证明.
解:图中的全等三角形共有 3 对,
分别是 △ADC 与 △ABC(SAS),
△FCD与 △FCB(SAS),
△FAD 与 △FAB(SAS).
【选自教材P21 随堂练习】
2. 如图,在正方形 ABCD 中,点 F 为对角线 AC 上一点,
连接 BF, DF。你能找出图中的全等三角形吗?选择其
中一对进行证明.
选择△FAD≌△FAB 证明,过程如下:
∵正方形 ABCD,
∴AD = AB,∠DAF =∠BAF,
又∵AF = AF,
∴△FAD≌△FAB.
【选自教材P21 随堂练习】
【选自教材P22 习题1.7 第1题】
3. 对角线长为 2 cm 的正方形,边长是多少?
解:∵ABCD 是正方形,
∴AB = BC,∠B = 90°
△ABC是等腰直角三角形,
AB2 + BC2 = AC2 = 4,
∴AB =
【选自教材P22 习题1.7 第2题】
4. 如图,四边形 ABCD 是正方形,△CBE 是等边三角形,
求∠AEB 的度数.
证明: ∵△BEC 是等边三角形,
∴BE = EC = BC = AB,
∴△ABE 是等腰三角形,
∴ ∠ABE = 90°-60° = 30 °
∴∠AEB = = 75 °
【选自教材P22 习题1.7 第3题】
5. 如图,A,B,C,D 四家工厂分别坐落在正方形城镇的四
个角上.仓库 P 和 Q 分别位于 AD 和 DC 上,且 PD = QC.
证明两条直路 BP = AQ 且 BP⊥AQ.
证明: 如图, AQ 与 BP 交于点 O.
在正方形 ABCD 中,
∵PD = QC, ∴DQ = AP .
又∵AB = AD ,∠D =∠PAB = 90°,
∴△ABP ≌△DAQ(SAS).
∴BP =AQ,∠DAQ=∠ABP .
∵∠ABP +∠APB= 90°=∠DAQ+∠APB.
∴∠AOP =90°.∴BP =AQ 且 BP ⊥ AQ.
6. 在一个正方形的花坛上,欲修建两条直的小路,使得两条
直的小路将花坛分成大小、形状完全相同的四部分(不考
虑道路的宽度).你有几种方法?画出图
【选自教材P22 习题1.7 第4题】
课堂小结
这节课你们都学会了哪些知识?
正方形的定义
正方形的性质
正方形的对角线相等并且互相垂直平分.
有一组邻边相等,并且有一个角是直角的平行四边形,叫做正方形.
正方形的四个角都是直角,四条边相等.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
