2024-2025学年湖北省武汉市汉阳一中、江夏一中高二(上)8月月考数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年湖北省武汉市汉阳一中、江夏一中高二(上)8月月考数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 143.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-13 00:00:00 | ||
图片预览




文档简介
2024-2025学年湖北省武汉市汉阳一中、江夏一中高二(上)8月月考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在空间直角坐标系中,为直线的一个方向向量,为平面的一个法向量,且,则( )
A. B. C. D.
2.已知直线,与平面,,,能使的充分条件是( )
A. ,, B. ,
C. , D. ,,
3.已知事件,互斥,它们都不发生的概率为,且,则( )
A. B. C. D.
4.已知甲袋中有个白球、个红球,乙袋中有个白球、个红球,各个球的大小与质地相同.现从甲、乙两袋中依次不放回地各取个球,若从甲袋中取出的个球的颜色不相同与从乙袋中取出的个球的颜色不相同的概率相等,则( )
A. B. C. 或 D. 或
5.水平放置的,用斜二测画法作出的直观图是如图所示的,其中,,则绕所在直线旋转一周后形成的几何体的表面积为( )
A. B.
C. D.
6.已知矩形中,是边的中点和交于点,将沿折起,在翻折过程中当与垂直时,异面直线和所成角的余弦值为( )
A. B. C. D.
7.已知是棱长为的正方体的一条体对角线,空间一点满足,是正方体的一条棱,则的最小值为( )
A. B. C. D.
8.在四棱锥中,,,,且,,则直线与平面所成角的正弦值的最大值为( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.设,为古典概率模型中的两个随机事件,以下命题正确的为( )
A. 若,,则当且仅当时,、是互斥事件
B. 若,,则是必然事件
C. 若,,则时,是独立事件
D. 若,,且,则,是独立事件
10.从某小区抽取户居民用户进行月用电量调查,发现他们的用电量都在之间,进行适当分组后每组为左闭右开区间,画出频率分布直方图如图所示,记直方图中六个小矩形的面积从左到右依次为,则( )
A. 的值为
B. 这户居民该月用电量的中位数为
C. 用电量落在区间内的户数为
D. 这户居民该月的平均用电量为
11.已知正方体的棱长为,点满足,其中,,点、分别是、的中点,下列选项不正确的是( )
A. 当时,的面积为定值
B. 当时,三棱锥的体积为定值
C. 存在使得与平面所成的角为
D. 当时,存在点,使得平面
三、填空题:本题共3小题,每小题5分,共15分。
12.一组数据:,,,,,,,,,,,,,的众数为,第三四分位数为,则 ______.
13.分制乒乓球比赛,每赢一球得分,当某局打成:后,每球交换发球权,先多得分的一方获胜,该局比赛结束甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为,乙发球时乙得分的概率为,各球的结果相互独立在某局打成:后,甲先发球,则甲以:获胜的概率为______.
14.已知三棱锥中,顶点在底面的射影恰好是内切圆的圆心,底面的最短边长为若三个侧面面积分别为,,,则顶点到底面的距离为______;三棱锥的外接球的表面积为______.
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,已知甲每轮猜对的概率为,乙每轮猜对的概率为在每轮活动中,甲和乙猜对与否互不影响,各轮结果也互不影响求:
甲在两轮活动中恰好猜对一个成语的概率;
“星队”在两轮活动中猜对个成语的概率.
16.本小题分
如图,平面,,,,,,.
求证:平面;
求直线与平面所成角的正弦值;
求二面角的正弦值.
17.本小题分
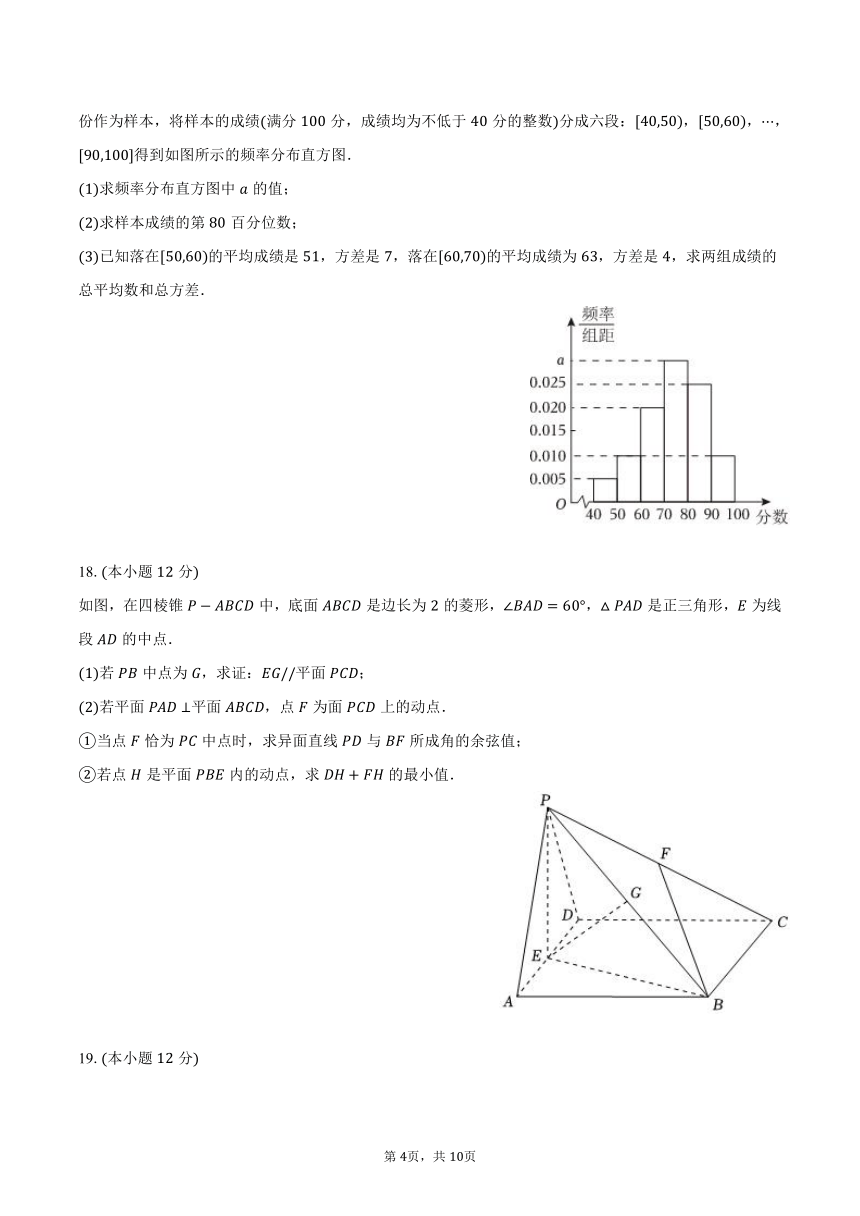
某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取份作为样本,将样本的成绩满分分,成绩均为不低于分的整数分成六段:,,,得到如图所示的频率分布直方图.
求频率分布直方图中的值;
求样本成绩的第百分位数;
已知落在的平均成绩是,方差是,落在的平均成绩为,方差是,求两组成绩的总平均数和总方差.
18.本小题分
如图,在四棱锥中,底面是边长为的菱形,,是正三角形,为线段的中点.
若中点为,求证:平面;
若平面平面,点为面上的动点.
当点恰为中点时,求异面直线与所成角的余弦值;
若点是平面内的动点,求的最小值.
19.本小题分
随着科技的发展,互联网也随之成熟,网络安全也涉及到一个国家经济,金融,政治等安全为提高中学生的网络安全意识和信息技术能力,某中学组织了一次信息技术创新比赛,参赛选手两人为一组,需要在规定时间内独自对两份不同的加密文件进行解密,每份文件只有一次解密机会已知甲每次解开密码的概率为,乙每次解开密码的概率为,每次是否解开密码也互不影响设甲成功解密一份文件,甲成功解密两份文件,乙成功解密一份文件,乙成功解密两份文件
Ⅰ已知概率,,
(ⅰ)求,的值.
(ⅱ)求甲、乙两次解密过程中一共解开密码三次的概率.
Ⅱ若,求甲、乙两次解密过程中一共解开密码三次的概率最小值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:根据题意,设表示甲两轮猜对个成语的事件,
甲每轮猜对的概率为,则猜错的概率为,
则.
设,分别表示甲两轮猜对个,个成语的事件,,分别表示乙两轮猜对个,个成语的事件,
.
设“两轮活动星队猜对个成语”,则,且与互斥,与,与分别相互独立,
所以.
因此,“星队”在两轮活动中猜对个成语的概率是.
16.解:因为,平面,平面,
所以平面,同理可知平面,
因为,所以平面平面,
因为平面,
所以平面;
建立如图所示的空间直角坐标系,
则,,,
得,,
设,
为平面的法向量,则,
不妨令,则,
设直线与平面所成角为,
所以,
所以直线与平面所成角的正弦值为;
设为平面的法向量,
则,即,
不妨令,可得,
所以,
所以二面角的正弦值为.
17.解:每组小矩形的面积之和为,
,
.
成绩落在内的频率为,
成绩落在内的频率为,
第百分位数落在内,
设第百分位数为,则,
解得,
即第百分位数为.
由图可知,成绩在的人数为,
成绩在的人数为,
故两组成绩的总平均数为,
总方差为.
18.解:证明:取中点,连接,
为线段的中点,,,
,,,,
四边形为平行四边形,
,平面,平面,
平面.
取的中点,连接,,
为中点,,,
就是异面直线和所成的角或所成角的补角,
平面平面,
平面平面,,平面,
平面,平面,
,菱形的边长为,,
与、是全等的正三角形,
、分别为、的中点,
,
在中,,
在中,,
,
在中,.
,,,平面,
平面,又为线段的中点,
,
,
要使最小只需最短即可,即为点到面的距离,
在中,,,
,
在中,,
,
,
解得,
的最小值为.
19.解:Ⅰ由题知:根据独立事件的概率乘法公式知,
,
解得:,;
由知:,,
设“甲、乙两次解密过程中一共解开密码三次”,
则,与互斥,与,与分别相互独立,
所以,
因此,甲,乙两次解密过程中一共解开密码三次的概率为.
Ⅱ由题知:,,
,,,,
设“甲、乙两次解密过程中一共解开密码三次”,
则,与互斥,与,与分别相互独立,
所以
,
,
,当且仅当时等号成立,
,
即甲、乙两次解密过程中一共解开密码三次的概率最小值为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在空间直角坐标系中,为直线的一个方向向量,为平面的一个法向量,且,则( )
A. B. C. D.
2.已知直线,与平面,,,能使的充分条件是( )
A. ,, B. ,
C. , D. ,,
3.已知事件,互斥,它们都不发生的概率为,且,则( )
A. B. C. D.
4.已知甲袋中有个白球、个红球,乙袋中有个白球、个红球,各个球的大小与质地相同.现从甲、乙两袋中依次不放回地各取个球,若从甲袋中取出的个球的颜色不相同与从乙袋中取出的个球的颜色不相同的概率相等,则( )
A. B. C. 或 D. 或
5.水平放置的,用斜二测画法作出的直观图是如图所示的,其中,,则绕所在直线旋转一周后形成的几何体的表面积为( )
A. B.
C. D.
6.已知矩形中,是边的中点和交于点,将沿折起,在翻折过程中当与垂直时,异面直线和所成角的余弦值为( )
A. B. C. D.
7.已知是棱长为的正方体的一条体对角线,空间一点满足,是正方体的一条棱,则的最小值为( )
A. B. C. D.
8.在四棱锥中,,,,且,,则直线与平面所成角的正弦值的最大值为( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.设,为古典概率模型中的两个随机事件,以下命题正确的为( )
A. 若,,则当且仅当时,、是互斥事件
B. 若,,则是必然事件
C. 若,,则时,是独立事件
D. 若,,且,则,是独立事件
10.从某小区抽取户居民用户进行月用电量调查,发现他们的用电量都在之间,进行适当分组后每组为左闭右开区间,画出频率分布直方图如图所示,记直方图中六个小矩形的面积从左到右依次为,则( )
A. 的值为
B. 这户居民该月用电量的中位数为
C. 用电量落在区间内的户数为
D. 这户居民该月的平均用电量为
11.已知正方体的棱长为,点满足,其中,,点、分别是、的中点,下列选项不正确的是( )
A. 当时,的面积为定值
B. 当时,三棱锥的体积为定值
C. 存在使得与平面所成的角为
D. 当时,存在点,使得平面
三、填空题:本题共3小题,每小题5分,共15分。
12.一组数据:,,,,,,,,,,,,,的众数为,第三四分位数为,则 ______.
13.分制乒乓球比赛,每赢一球得分,当某局打成:后,每球交换发球权,先多得分的一方获胜,该局比赛结束甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为,乙发球时乙得分的概率为,各球的结果相互独立在某局打成:后,甲先发球,则甲以:获胜的概率为______.
14.已知三棱锥中,顶点在底面的射影恰好是内切圆的圆心,底面的最短边长为若三个侧面面积分别为,,,则顶点到底面的距离为______;三棱锥的外接球的表面积为______.
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,已知甲每轮猜对的概率为,乙每轮猜对的概率为在每轮活动中,甲和乙猜对与否互不影响,各轮结果也互不影响求:
甲在两轮活动中恰好猜对一个成语的概率;
“星队”在两轮活动中猜对个成语的概率.
16.本小题分
如图,平面,,,,,,.
求证:平面;
求直线与平面所成角的正弦值;
求二面角的正弦值.
17.本小题分
某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取份作为样本,将样本的成绩满分分,成绩均为不低于分的整数分成六段:,,,得到如图所示的频率分布直方图.
求频率分布直方图中的值;
求样本成绩的第百分位数;
已知落在的平均成绩是,方差是,落在的平均成绩为,方差是,求两组成绩的总平均数和总方差.
18.本小题分
如图,在四棱锥中,底面是边长为的菱形,,是正三角形,为线段的中点.
若中点为,求证:平面;
若平面平面,点为面上的动点.
当点恰为中点时,求异面直线与所成角的余弦值;
若点是平面内的动点,求的最小值.
19.本小题分
随着科技的发展,互联网也随之成熟,网络安全也涉及到一个国家经济,金融,政治等安全为提高中学生的网络安全意识和信息技术能力,某中学组织了一次信息技术创新比赛,参赛选手两人为一组,需要在规定时间内独自对两份不同的加密文件进行解密,每份文件只有一次解密机会已知甲每次解开密码的概率为,乙每次解开密码的概率为,每次是否解开密码也互不影响设甲成功解密一份文件,甲成功解密两份文件,乙成功解密一份文件,乙成功解密两份文件
Ⅰ已知概率,,
(ⅰ)求,的值.
(ⅱ)求甲、乙两次解密过程中一共解开密码三次的概率.
Ⅱ若,求甲、乙两次解密过程中一共解开密码三次的概率最小值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:根据题意,设表示甲两轮猜对个成语的事件,
甲每轮猜对的概率为,则猜错的概率为,
则.
设,分别表示甲两轮猜对个,个成语的事件,,分别表示乙两轮猜对个,个成语的事件,
.
设“两轮活动星队猜对个成语”,则,且与互斥,与,与分别相互独立,
所以.
因此,“星队”在两轮活动中猜对个成语的概率是.
16.解:因为,平面,平面,
所以平面,同理可知平面,
因为,所以平面平面,
因为平面,
所以平面;
建立如图所示的空间直角坐标系,
则,,,
得,,
设,
为平面的法向量,则,
不妨令,则,
设直线与平面所成角为,
所以,
所以直线与平面所成角的正弦值为;
设为平面的法向量,
则,即,
不妨令,可得,
所以,
所以二面角的正弦值为.
17.解:每组小矩形的面积之和为,
,
.
成绩落在内的频率为,
成绩落在内的频率为,
第百分位数落在内,
设第百分位数为,则,
解得,
即第百分位数为.
由图可知,成绩在的人数为,
成绩在的人数为,
故两组成绩的总平均数为,
总方差为.
18.解:证明:取中点,连接,
为线段的中点,,,
,,,,
四边形为平行四边形,
,平面,平面,
平面.
取的中点,连接,,
为中点,,,
就是异面直线和所成的角或所成角的补角,
平面平面,
平面平面,,平面,
平面,平面,
,菱形的边长为,,
与、是全等的正三角形,
、分别为、的中点,
,
在中,,
在中,,
,
在中,.
,,,平面,
平面,又为线段的中点,
,
,
要使最小只需最短即可,即为点到面的距离,
在中,,,
,
在中,,
,
,
解得,
的最小值为.
19.解:Ⅰ由题知:根据独立事件的概率乘法公式知,
,
解得:,;
由知:,,
设“甲、乙两次解密过程中一共解开密码三次”,
则,与互斥,与,与分别相互独立,
所以,
因此,甲,乙两次解密过程中一共解开密码三次的概率为.
Ⅱ由题知:,,
,,,,
设“甲、乙两次解密过程中一共解开密码三次”,
则,与互斥,与,与分别相互独立,
所以
,
,
,当且仅当时等号成立,
,
即甲、乙两次解密过程中一共解开密码三次的概率最小值为.
第1页,共1页
同课章节目录
