6.4数据的离散程度——八年级数学北师大版(2012)上册课时优化训练(含详解)
文档属性
| 名称 | 6.4数据的离散程度——八年级数学北师大版(2012)上册课时优化训练(含详解) |  | |
| 格式 | doc | ||
| 文件大小 | 464.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-13 20:46:17 | ||
图片预览



文档简介
6.4数据的离散程度——八年级数学北师大版(2012)上册课时优化训练
1.有31位学生参加学校举行的“最强大脑”智力游戏比赛,比赛结束后根据每个学生的最后得分计算出中位数、平均数、众数和方差,如果去掉一个最高分和一个最低分,则一定不发生变化的是( )
A.中位数 B.平均数 C.众数 D.方差
2.袁隆平院士被誉为“世界杂交水稻之父”,他研究的水稻,不仅高产,而且抗倒伏.在某次实验中,他的团队对甲、乙两种水稻品种进行产量稳定实验,各选取了8块条件相同的试验田,同时播种并核定亩产,结果甲、乙两种水稻的平均产量均为1200千克/亩,方差为,.为保证产量稳定,适合推广的品种为( )
A.甲 B.乙 C.甲、乙均可 D.无法确定
3.某校举行“遵守交通安全,从我做起”演讲比赛,5位评委给选手甲的评分如下:90,90,93,92,90,则这组数据的众数和方差分别是( )
A.93,1.6 B.90,1.6 C.93,1 D.90,1
4.校园歌手赛中,7位评委打分得到了一组数据,为了比赛更加公平,这组数据要去掉一个最高分和一个最低分得到一组新数据,那么对比原数据,下列结论一定正确的是( )
A.新数据的中位数一定不变 B.新数据的平均数一定变大
C.新数据的方差一定变小 D.新数据的众数一定不变
5.为了解“睡眠管理”落实情况,某初中学校随机调查50名学生每天平均睡眠时间(时间均保留整数),将样本数据绘制成统计图(如图),其中有两个数据被遮盖关于睡眠时间的统计量中,与被遮盖的数据无关的是( )
A.平均数 B.中位数 C.众数 D.方差
6.一位射击运动员在一次训练效果测试中射击了10次,成绩如图所示,对于这10次射击的成绩有如下结论,其中不正确的是( )
A.众数是8 B.中位数是8 C.平均数是8 D.方差是1
7.甲、乙两名技工每天的基本工作量都是做10件产品,质检部将他们一周的优等品件数绘制如图的折线统计图,根据统计图中的数据,下列说法正确的是( )
A.甲、乙的优等品件数的平均数相同
B.甲、乙的优等品件数的中位数相同
C.甲的优等品件数的众数小于乙的众数
D.甲的优等品件数的方差大于乙的方差
8.小庆、小铁、小娜、小萌四名同学均从1,2,3,4,5,6这六个数字中选出四个数字,玩猜数游戏.下列选项中,能确定该同学选出的四个数字含有1的是( )
A.小庆选出四个数字的方差等于 B.小铁选出四个数字的方差等于
C.小娜选出四个数字的平均数等于 D.小萌选出四个数字的极差等于4
9.校运会上,七、八、九年级同学分别组建了红、黄、蓝三支仪仗队,各队队员身高()的平均数()与方差()如表所示,则三支仪仗队中身高最整齐的______.
红队 黄队 蓝队
165 168 170
12.75 8.8 10.45
10.某校五个绿化小组一天的植树的棵数如下:10,10,12,x,8.已知这组数据的平均数是10,那么这组数据的方差是___________.
11.甲乙两班举行一分钟跳绳比赛,参赛学生每分钟跳绳次数的统计结果如表:
班级 参加人数 中位数 方差 平均数
甲 45 109 181 110
乙 45 111 108 110
某同学分析如表后得到如下结论:①甲,乙两班学生平均成绩相同;②乙班优秀人数多于甲班优秀人数(每分钟跳绳次为优秀);③甲班成绩的波动比乙班大,则正确结论的序号是______.
12.若一组数据,,,…,的平均数为4,方差为2,则,,,…,的方差为__________.
13.在一次体操比赛中,6个裁判员对某一运动员的打分数据(动作完成分)如下:
9.68.88.88.98.68.7
对打分数据有以下两种处理方式:
方式一:不去掉任何数据,用6个原始数据进行统计:
平均分 中位数 方差
8.9 a 0.107
方式二:去掉一个最高分和一个最低分,用剩余的4个数据进行统计:
平均分 中位数 方差
b 8.8 c
(1)______,______,______;
(2)你认为把哪种方式统计出的平均分作为该运动员的最终得分更合理?写出你的判定并说明理由.
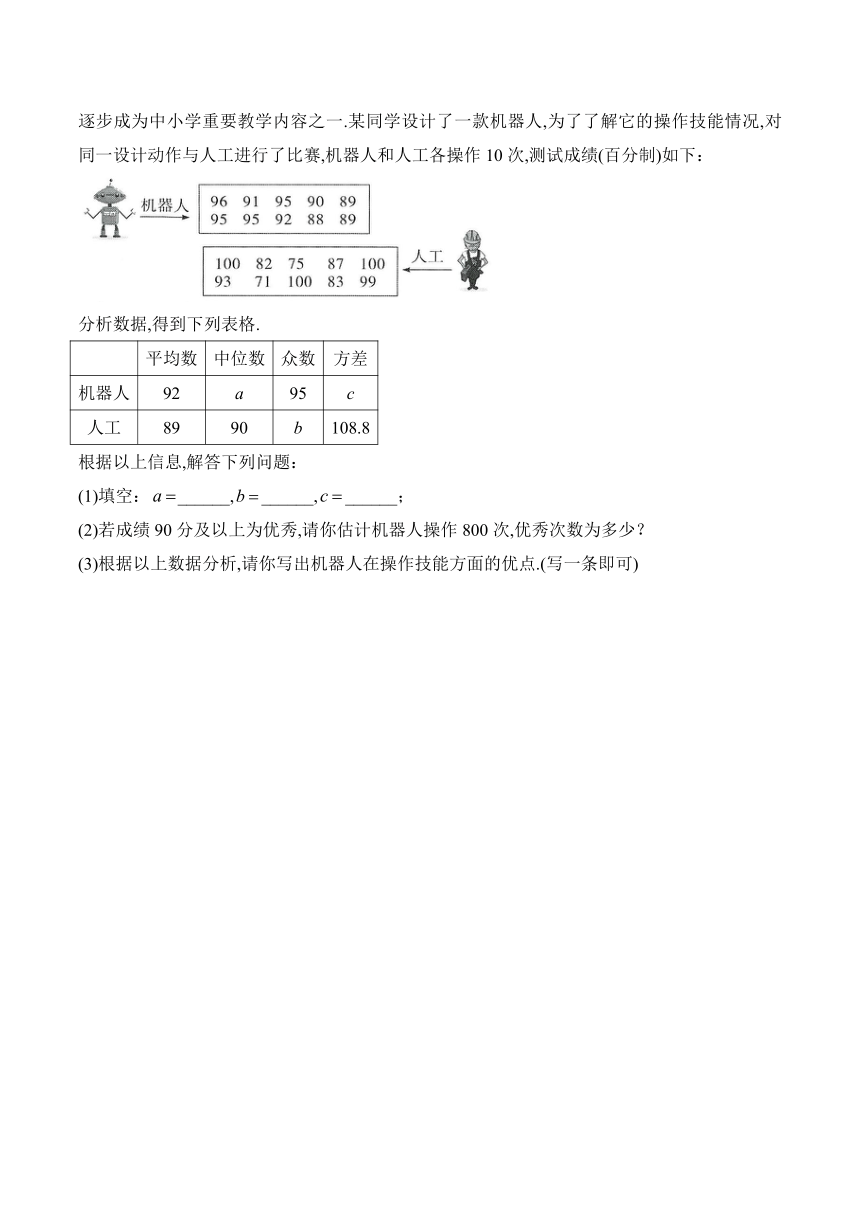
14.当前各国都高度重视人工智能并视其为提升国家竞争力的重要力量,随着人工智能与各个垂直领域的不断深入融合,普通公民也越来越需要具备人工智能的基本知识和应用能力,人工智能逐步成为中小学重要教学内容之一.某同学设计了一款机器人,为了了解它的操作技能情况,对同一设计动作与人工进行了比赛,机器人和人工各操作10次,测试成绩(百分制)如下:
分析数据,得到下列表格.
平均数 中位数 众数 方差
机器人 92 a 95 c
人工 89 90 b 108.8
根据以上信息,解答下列问题:
(1)填空:______,______,______;
(2)若成绩90分及以上为优秀,请你估计机器人操作800次,优秀次数为多少?
(3)根据以上数据分析,请你写出机器人在操作技能方面的优点.(写一条即可)
答案以及解析
1.答案:A
解析:由中位数的定义可知,去掉一个最高分和一个最低分对中位数没有影响,
所以中位数一定不发生变化,
故选:A.
2.答案:A
解析:,,
,
为保证产量稳定,适合推广的品种为甲,
故选:A.
3.答案:B
解析:90出现3次,出现次数最多,则众数为90,
平均数为
∴方差为
故选:B.
4.答案:A
解析:统计每位选手得分时,会去掉一个最高分和一个最低分,这样做不会对数据的中间的数产生影响,即中位数.故新数据的中位数一定不变
故选:A.
5.答案:B
解析:根据题意可得,计算平均数、方差需要全部数据,故A、D不符合题意;
∵,
∴无法确定众数分布在哪一组,故C不符合题意;
从统计图可得:前三组的数据共有,
共有50名学生,中位数为第25与26位的平均数,
∴已知的数据中中位数确定,且不受后面数据的影响,
故选:B.
6.答案:D
解析:由题意得:这10次成绩的环数为:6,7,7,8,8,8,8,9,9,10(已按照从小到大的顺序排列);
所以这10个数据的众数是8环,中位数是8环,平均数环,
方差环.
所以在以上4个选项中,D选项是错误的.
故选:D.
7.答案:C
解析:A、,,故该选项错误,不符合题意;
B、甲优等品件数的中位数为:7,乙优等品件数的中位数为:9,故该选项错误,不符合题意;
C、甲的优等品件数的众数为8和7,乙的优等品件数的众数为9,故该选项正确,符合题意;
D、,,故该选项错误,不符合题意;
故选:C.
8.答案:A
解析:A、假设选出的数据没有1,则选出的数据为2,3,5,6时,方差最大,此时,方差为;当数据为1,2,5,6时,,,故该选项符合题意;
B、当该同学选出的四个数字为2,3,5,6时,,,故该选项不符合题意;
C、当该同学选出的四个数字为2,3,4,5时,,故该选项不符合题意;
D、当选出的数据为2,4,5,6或2,3,4,6时,极差也是4,故该选项不符合题意;
故选:A.
9.答案:黄队
解析:由表知:黄队身高的方差最小,
所以三支仪仗队中身高最整齐的黄队,
故答案为:黄队.
10.答案:1.6
解析:试题:∵数据10,10,12,x,8的平均数是10,
∴,解得.
∴这组数据的方差是.
故答案为:1.6
11.答案:①②③
解析:甲、乙两班的平均数都是110,故①正确,
∵甲班的中位数是109,乙班的中位数是111,乙班中位数比甲班的大,
∴乙班优秀的人数多于甲班优秀的人数,故②正确,
∵甲班的方差大于乙班的方差,
∴甲班的波动情况大,故③正确;
综上所述,①②③都正确,
故答案为①②③
12.答案:8
解析:∵一组数据,,,…,的平均数为4,方差为2,
∴,
∴,
则,,,…,的平均数为
则,,,…,的方差为
,
故答案为:8.
13.答案:(1)8.8,8.8,0.005
(2)答案不唯一,理由见解析
解析:(1)将数据排序得:8.68.78.88.88.99.6
则位于中间的数为:8.8,8.8,
中位数
平均数
方差
故答案为:8.8,8.8;0.005;
(2)答案不唯一,
参考答案一:方式二更合理.
理由:方式二去掉了最高分和最低分,减少了极端分值对平均分的影响,比方式一更合理.
参考答案二:方式一更合理.
理由:方式一没有去掉任何数据,用6个原始数据计算平均分,能全面反映所有评委的打分结果,比方式二更合理.
14.答案:(1)91.5;100;8.2
(2)估计机器人操作800次,优秀次数约为560(次)
(3)见解析
解析:(1)把机器人数据从小到大排列,排在中间的两个数分别是91和92,故中位数
;
在人工数据中,100出现的次数最多,故众数
;
;
(2)(次)
答:估计机器人操作800次,优秀次数约为560(次);
(3)机器人的样本数据的平均数高于人工,方差较小,可以推断其优势在于操作技能水平较高的同时还能保持稳定.
1.有31位学生参加学校举行的“最强大脑”智力游戏比赛,比赛结束后根据每个学生的最后得分计算出中位数、平均数、众数和方差,如果去掉一个最高分和一个最低分,则一定不发生变化的是( )
A.中位数 B.平均数 C.众数 D.方差
2.袁隆平院士被誉为“世界杂交水稻之父”,他研究的水稻,不仅高产,而且抗倒伏.在某次实验中,他的团队对甲、乙两种水稻品种进行产量稳定实验,各选取了8块条件相同的试验田,同时播种并核定亩产,结果甲、乙两种水稻的平均产量均为1200千克/亩,方差为,.为保证产量稳定,适合推广的品种为( )
A.甲 B.乙 C.甲、乙均可 D.无法确定
3.某校举行“遵守交通安全,从我做起”演讲比赛,5位评委给选手甲的评分如下:90,90,93,92,90,则这组数据的众数和方差分别是( )
A.93,1.6 B.90,1.6 C.93,1 D.90,1
4.校园歌手赛中,7位评委打分得到了一组数据,为了比赛更加公平,这组数据要去掉一个最高分和一个最低分得到一组新数据,那么对比原数据,下列结论一定正确的是( )
A.新数据的中位数一定不变 B.新数据的平均数一定变大
C.新数据的方差一定变小 D.新数据的众数一定不变
5.为了解“睡眠管理”落实情况,某初中学校随机调查50名学生每天平均睡眠时间(时间均保留整数),将样本数据绘制成统计图(如图),其中有两个数据被遮盖关于睡眠时间的统计量中,与被遮盖的数据无关的是( )
A.平均数 B.中位数 C.众数 D.方差
6.一位射击运动员在一次训练效果测试中射击了10次,成绩如图所示,对于这10次射击的成绩有如下结论,其中不正确的是( )
A.众数是8 B.中位数是8 C.平均数是8 D.方差是1
7.甲、乙两名技工每天的基本工作量都是做10件产品,质检部将他们一周的优等品件数绘制如图的折线统计图,根据统计图中的数据,下列说法正确的是( )
A.甲、乙的优等品件数的平均数相同
B.甲、乙的优等品件数的中位数相同
C.甲的优等品件数的众数小于乙的众数
D.甲的优等品件数的方差大于乙的方差
8.小庆、小铁、小娜、小萌四名同学均从1,2,3,4,5,6这六个数字中选出四个数字,玩猜数游戏.下列选项中,能确定该同学选出的四个数字含有1的是( )
A.小庆选出四个数字的方差等于 B.小铁选出四个数字的方差等于
C.小娜选出四个数字的平均数等于 D.小萌选出四个数字的极差等于4
9.校运会上,七、八、九年级同学分别组建了红、黄、蓝三支仪仗队,各队队员身高()的平均数()与方差()如表所示,则三支仪仗队中身高最整齐的______.
红队 黄队 蓝队
165 168 170
12.75 8.8 10.45
10.某校五个绿化小组一天的植树的棵数如下:10,10,12,x,8.已知这组数据的平均数是10,那么这组数据的方差是___________.
11.甲乙两班举行一分钟跳绳比赛,参赛学生每分钟跳绳次数的统计结果如表:
班级 参加人数 中位数 方差 平均数
甲 45 109 181 110
乙 45 111 108 110
某同学分析如表后得到如下结论:①甲,乙两班学生平均成绩相同;②乙班优秀人数多于甲班优秀人数(每分钟跳绳次为优秀);③甲班成绩的波动比乙班大,则正确结论的序号是______.
12.若一组数据,,,…,的平均数为4,方差为2,则,,,…,的方差为__________.
13.在一次体操比赛中,6个裁判员对某一运动员的打分数据(动作完成分)如下:
9.68.88.88.98.68.7
对打分数据有以下两种处理方式:
方式一:不去掉任何数据,用6个原始数据进行统计:
平均分 中位数 方差
8.9 a 0.107
方式二:去掉一个最高分和一个最低分,用剩余的4个数据进行统计:
平均分 中位数 方差
b 8.8 c
(1)______,______,______;
(2)你认为把哪种方式统计出的平均分作为该运动员的最终得分更合理?写出你的判定并说明理由.
14.当前各国都高度重视人工智能并视其为提升国家竞争力的重要力量,随着人工智能与各个垂直领域的不断深入融合,普通公民也越来越需要具备人工智能的基本知识和应用能力,人工智能逐步成为中小学重要教学内容之一.某同学设计了一款机器人,为了了解它的操作技能情况,对同一设计动作与人工进行了比赛,机器人和人工各操作10次,测试成绩(百分制)如下:
分析数据,得到下列表格.
平均数 中位数 众数 方差
机器人 92 a 95 c
人工 89 90 b 108.8
根据以上信息,解答下列问题:
(1)填空:______,______,______;
(2)若成绩90分及以上为优秀,请你估计机器人操作800次,优秀次数为多少?
(3)根据以上数据分析,请你写出机器人在操作技能方面的优点.(写一条即可)
答案以及解析
1.答案:A
解析:由中位数的定义可知,去掉一个最高分和一个最低分对中位数没有影响,
所以中位数一定不发生变化,
故选:A.
2.答案:A
解析:,,
,
为保证产量稳定,适合推广的品种为甲,
故选:A.
3.答案:B
解析:90出现3次,出现次数最多,则众数为90,
平均数为
∴方差为
故选:B.
4.答案:A
解析:统计每位选手得分时,会去掉一个最高分和一个最低分,这样做不会对数据的中间的数产生影响,即中位数.故新数据的中位数一定不变
故选:A.
5.答案:B
解析:根据题意可得,计算平均数、方差需要全部数据,故A、D不符合题意;
∵,
∴无法确定众数分布在哪一组,故C不符合题意;
从统计图可得:前三组的数据共有,
共有50名学生,中位数为第25与26位的平均数,
∴已知的数据中中位数确定,且不受后面数据的影响,
故选:B.
6.答案:D
解析:由题意得:这10次成绩的环数为:6,7,7,8,8,8,8,9,9,10(已按照从小到大的顺序排列);
所以这10个数据的众数是8环,中位数是8环,平均数环,
方差环.
所以在以上4个选项中,D选项是错误的.
故选:D.
7.答案:C
解析:A、,,故该选项错误,不符合题意;
B、甲优等品件数的中位数为:7,乙优等品件数的中位数为:9,故该选项错误,不符合题意;
C、甲的优等品件数的众数为8和7,乙的优等品件数的众数为9,故该选项正确,符合题意;
D、,,故该选项错误,不符合题意;
故选:C.
8.答案:A
解析:A、假设选出的数据没有1,则选出的数据为2,3,5,6时,方差最大,此时,方差为;当数据为1,2,5,6时,,,故该选项符合题意;
B、当该同学选出的四个数字为2,3,5,6时,,,故该选项不符合题意;
C、当该同学选出的四个数字为2,3,4,5时,,故该选项不符合题意;
D、当选出的数据为2,4,5,6或2,3,4,6时,极差也是4,故该选项不符合题意;
故选:A.
9.答案:黄队
解析:由表知:黄队身高的方差最小,
所以三支仪仗队中身高最整齐的黄队,
故答案为:黄队.
10.答案:1.6
解析:试题:∵数据10,10,12,x,8的平均数是10,
∴,解得.
∴这组数据的方差是.
故答案为:1.6
11.答案:①②③
解析:甲、乙两班的平均数都是110,故①正确,
∵甲班的中位数是109,乙班的中位数是111,乙班中位数比甲班的大,
∴乙班优秀的人数多于甲班优秀的人数,故②正确,
∵甲班的方差大于乙班的方差,
∴甲班的波动情况大,故③正确;
综上所述,①②③都正确,
故答案为①②③
12.答案:8
解析:∵一组数据,,,…,的平均数为4,方差为2,
∴,
∴,
则,,,…,的平均数为
则,,,…,的方差为
,
故答案为:8.
13.答案:(1)8.8,8.8,0.005
(2)答案不唯一,理由见解析
解析:(1)将数据排序得:8.68.78.88.88.99.6
则位于中间的数为:8.8,8.8,
中位数
平均数
方差
故答案为:8.8,8.8;0.005;
(2)答案不唯一,
参考答案一:方式二更合理.
理由:方式二去掉了最高分和最低分,减少了极端分值对平均分的影响,比方式一更合理.
参考答案二:方式一更合理.
理由:方式一没有去掉任何数据,用6个原始数据计算平均分,能全面反映所有评委的打分结果,比方式二更合理.
14.答案:(1)91.5;100;8.2
(2)估计机器人操作800次,优秀次数约为560(次)
(3)见解析
解析:(1)把机器人数据从小到大排列,排在中间的两个数分别是91和92,故中位数
;
在人工数据中,100出现的次数最多,故众数
;
;
(2)(次)
答:估计机器人操作800次,优秀次数约为560(次);
(3)机器人的样本数据的平均数高于人工,方差较小,可以推断其优势在于操作技能水平较高的同时还能保持稳定.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
