22.1一元二次方程(同步课件)-九年级数学上册同步精品课堂(华东师大版)
文档属性
| 名称 | 22.1一元二次方程(同步课件)-九年级数学上册同步精品课堂(华东师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-18 09:45:45 | ||
图片预览








文档简介
(共29张PPT)
22.1 一元二次方程
数学(华东师大版)
九年级 上册
第22章 一元二次方程
学习目标
1.了解一元二次方程的概念;
2.掌握一元二次方程的一般形式ax2+bx+c=0(a, b, c为常数,a≠0)
3.能根据具体问题的数量关系,建立一元二次方程的模型;
温故知新
一元一次方程
未知量
未知量的最高次幂
一个未知量
未知量的最高次幂是1
【提示】
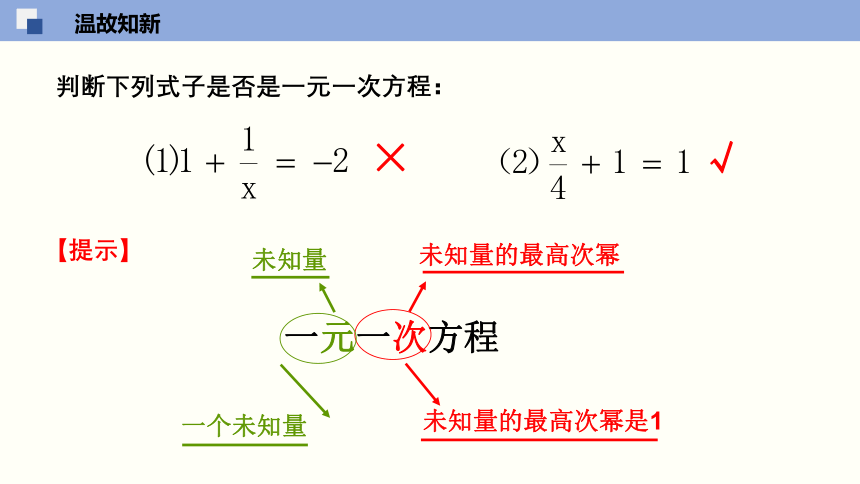
判断下列式子是否是一元一次方程:
×
√
导入新课
绿苑小区规划设计时,准备在每两幢楼房之间,设置一块面积为900平方米的长方形绿地,并且长比宽多10米,那么绿地的长和宽各为多少?
讲授新课
知识点一 一元二次方程的概念
问题1:请通过类比一元一次方程一般形式(ax + b = 0),对下面所得方程进行整理.
(1) x2 = 64 ; (2)x(x + 10) = 1200.
(1) x2 – 64 = 0 ;
(2) x2 + 10x – 1200 = 0.
问题2:上述两个方程有什么共同特点?
1.只含有一个未知数; 2.未知数的最高次数是2;
3.整式方程.
讲授新课
只含有一个未知数x的整式方程,并且都可以化为ax2+bx+c=0(a,b,c为常数, a≠0)的形式,这样的方程叫做一元二次方程.
ax2+bx +c = 0(a , b , c为常数, a≠0)
ax2 称为二次项, a 称为二次项系数.
bx 称为一次项, b 称为一次项系数.
c 称为常数项.
※一元二次方程的概念
※一元二次方程的一般形式
讲授新课
思考 为什么一般形式中ax2+bx+c=0要限制a≠0,b、c 可以为零吗?
当 a = 0 时
bx+c = 0
当 a ≠ 0 , b = 0时 ,
ax2+c = 0
当 a ≠ 0 , c = 0时 ,
ax2+bx = 0
当 a ≠ 0 ,b = c =0时 ,
ax2 = 0
总结:只要满足a ≠ 0 ,b , c 可以为任意实数.
讲授新课
判断下列方程是否为一元二次方程.
(1) 1-x3=0
(2) 2(x2-1)=3y
(3) y(y-3)=-4
(4) (x+1)(x-2)=x2
(5) 3x2=
(6) ax2+bx+c=0(a、b、c为常数)
否
否
是
否
否
a ≠ 0
否
讲授新课
典例精析
【例1】下列选项中,关于x的一元二次方程的是( )
C
不是整式方程
含两个未知数
化简整理成x2-3x+2=0
少了限制条件a≠0
【点睛】判断一个方程是不是一元二次方程,首先看是不是整式方程;如是再进一步化简整理后再作判断.
讲授新课
练一练
1、如果方程(m-3)·xm2-7-x+3=0 是关于x的一元二次方程,那么m 的值为( )
A. ±3 B. 3
C. -3 D. 以上都不对
C
讲授新课
2、关于x的方程(k - 3) x2 +2x - 1=0,当k 时,是一元二次方程.
3、关于x的方程(k2 - 1) x2 +2 (k - 1) x + 2k + 2 = 0,当k 时,是一元二次方程.当k 时,是一元一次方程.
≠3
≠±1
=-1
讲授新课
方 程 一般形式 二次项系数 一次项系数 常数项
x(19-2x)=24
x2=2
x2+(x-1 )2 =25
x2-2=0
试一试:
1
0
-2
2x2-19x+24=0
2
-19
24
2x2-2x-24=0
2
-2
-24
讲授新课
4、a为何值时,下列方程为一元二次方程?
(1)ax2-x=2x2
(2) (a-1)x |a|+1 -2x-7=0.
解:(1)将方程式转化为一般形式,得(a-2)x2-x=0,
∴当a-2≠0,即a≠2时,原方程是一元二次方程;
(2)由+1 =2,且a-1≠0得,
当a=-1时,原方程是一元二次方程.
讲授新课
【例2】将方程3x(x-1)=5(x+2)化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数.
解:
去括号,得
3x2-3x=5x+10.
移项、合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
二次项是3x2,系数是3;一次项是-8x,系数是-8;常数项是-10.
讲授新课
1.若关于x的方程(m-2)x2+mx-3=0是一元二次方程,则m的取值范围是( )
A.m≠2 B.m=2 C.m>2 D.m≠0
A
2、如果方程(m-2)xm2-2-mx+3=0是关于x的一元二次方程,那么m的值为_________.
-2
讲授新课
3. 把下列方程化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.
(1) x2-x=2;
(2) 4x+1=x2;
解:(1)将方程化成一般形式,得x2-x-2=0,
二次项系数、一次项系数和常数项分别是1、-1、-2.
(2)将方程转化成一般形式,得x2-4x-1=0,
二次项系数、一次项系数和常数项分别是1、-4、-1.
讲授新课
知识点二 建立一元二次方程的模型
用方程描述下列问题中的数量关系:
(1)一张面积是240 cm2的长方形彩纸,长比宽多8cm,设它的宽为xcm,可得方程_______________.
x(8+x)=240
(2)一枚圆形古钱币的中间是一个边长为1cm 的正方形孔,已知正方形面积是圆面积的 ,设圆的半径为xcm,可得方程___________.
πx2=9
讲授新课
(3)两个连续奇数的积为323,设其中的一个奇数为x,可得方程__________________________.
x(x+2)=323或x(x-2)=323
(4)某工厂经过两年时间将某种产品的产量从每年14 400台提高到16 900台,设平均每年增长的百分率为x,可得方程______________________.
14 400(1+x)2=16 900
讲授新课
典例精析
【例3】观察下面等式:
102 + 112 + 122 = 132 + 142
你还能找到其他的五个连续整数,使前三个数的平方和等于后两个数的平方和吗?
解:如果设五个连续整数中的第一个数为x,那么后面四个数依次可表示为: , , , .
根据题意,可得方程:
x+1
x+2
x+3
x+4
x2 + (x + 1)2 + (x + 2)2 = (x + 3)2 + (x + 4)2.
x2 - 8x - 20=0(一般式).
讲授新课
练一练
解:由勾股定理可知,滑动前梯子底端距墙 m.
如果设梯子底端滑动x m ,那么滑动后梯子底端距墙 m ,
根据题意,可得方程:
1、如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
6
x+6
72 + (x + 6)2 = 102.
x2 + 12 x - 15 = 0(一般式).
10m
8m
1m
xm
当堂检测
1. 下列哪些是一元二次方程?
(1)3x+2=5x-2
(2)x2=0
(3)(x+3)(2x-4)=x2
(4)3y2=(3y+1)(y-2)
(5)x2=x3+x2-1
(6)3x2=5x-1
当堂检测
2.填空:
方程 一般形式 二次项系数 一次项系数 常数项
-2
1
3
1
3
-5
4
0
-5
3
-2
当堂检测
3.将一元二次方程
A. B.
C. D.
C
当堂检测
4. 一元二次方程
A. 2,5,6 B. 5,2,6
C. 2,5,-6 D. 5,2,-6
C
当堂检测
5.已知关于x的一元二次方程(m-3)x2+m2x=9x+5化为一般形式后不含一次项,则m的值为 ( )
A. 0 B. ±3 C. 3 D. -3
D
当堂检测
6.如图,有一面积为600m2的长方形鸡场,鸡场的一边靠墙 (墙长35m) ,另三边用竹篱笆围成,其中一边开有1m的门,竹篱笆的总长为69m.设鸡场垂直于墙的一边为xm,则列方程正确的是( )
A.x(69+1-2x)=600 B.x(69-1-2x)=600
C.x(69-2x)=600 D.x(35+1-2x)=600
A
当堂检测
7. 已知关于x的方程(m-1)+(m-2)x-1=0,回答下面的问题:
(1) 若方程是一元二次方程,求m的值.
解:(1)根据题意,得m2+1=2,且m-1≠0,解得m=-1.
(2)若方程是一元一次方程,则m的值是否存在?若存在,请求出m的值,并求出方程的解.
解:(2) 存在 有两种情况:
① 当满足m2+1=1,且(m-1)+(m-2)≠0时,解得m=0,
则方程变为-3x-1=0,解得x=-;
② 当满足m-1=0,且m-2≠0时,解得m=1,
则方程变为-x-1=0,解得x=-1
课堂小结
一元二次方程
只含有一个未知数x的整式方程,并且都可以
化为ax2+bx+c=0(a,b,c为常数,a≠0)的形式.
概念
一般式:ax2+bx+c=0(a , b , c为常数, a≠0)
ax2 称为二次项,a 称为二次项系数.
bx 称为一次项,b 称为一次项系数.
c 称为常数项.
建立一元二次方程模型
谢 谢~
22.1 一元二次方程
数学(华东师大版)
九年级 上册
第22章 一元二次方程
学习目标
1.了解一元二次方程的概念;
2.掌握一元二次方程的一般形式ax2+bx+c=0(a, b, c为常数,a≠0)
3.能根据具体问题的数量关系,建立一元二次方程的模型;
温故知新
一元一次方程
未知量
未知量的最高次幂
一个未知量
未知量的最高次幂是1
【提示】
判断下列式子是否是一元一次方程:
×
√
导入新课
绿苑小区规划设计时,准备在每两幢楼房之间,设置一块面积为900平方米的长方形绿地,并且长比宽多10米,那么绿地的长和宽各为多少?
讲授新课
知识点一 一元二次方程的概念
问题1:请通过类比一元一次方程一般形式(ax + b = 0),对下面所得方程进行整理.
(1) x2 = 64 ; (2)x(x + 10) = 1200.
(1) x2 – 64 = 0 ;
(2) x2 + 10x – 1200 = 0.
问题2:上述两个方程有什么共同特点?
1.只含有一个未知数; 2.未知数的最高次数是2;
3.整式方程.
讲授新课
只含有一个未知数x的整式方程,并且都可以化为ax2+bx+c=0(a,b,c为常数, a≠0)的形式,这样的方程叫做一元二次方程.
ax2+bx +c = 0(a , b , c为常数, a≠0)
ax2 称为二次项, a 称为二次项系数.
bx 称为一次项, b 称为一次项系数.
c 称为常数项.
※一元二次方程的概念
※一元二次方程的一般形式
讲授新课
思考 为什么一般形式中ax2+bx+c=0要限制a≠0,b、c 可以为零吗?
当 a = 0 时
bx+c = 0
当 a ≠ 0 , b = 0时 ,
ax2+c = 0
当 a ≠ 0 , c = 0时 ,
ax2+bx = 0
当 a ≠ 0 ,b = c =0时 ,
ax2 = 0
总结:只要满足a ≠ 0 ,b , c 可以为任意实数.
讲授新课
判断下列方程是否为一元二次方程.
(1) 1-x3=0
(2) 2(x2-1)=3y
(3) y(y-3)=-4
(4) (x+1)(x-2)=x2
(5) 3x2=
(6) ax2+bx+c=0(a、b、c为常数)
否
否
是
否
否
a ≠ 0
否
讲授新课
典例精析
【例1】下列选项中,关于x的一元二次方程的是( )
C
不是整式方程
含两个未知数
化简整理成x2-3x+2=0
少了限制条件a≠0
【点睛】判断一个方程是不是一元二次方程,首先看是不是整式方程;如是再进一步化简整理后再作判断.
讲授新课
练一练
1、如果方程(m-3)·xm2-7-x+3=0 是关于x的一元二次方程,那么m 的值为( )
A. ±3 B. 3
C. -3 D. 以上都不对
C
讲授新课
2、关于x的方程(k - 3) x2 +2x - 1=0,当k 时,是一元二次方程.
3、关于x的方程(k2 - 1) x2 +2 (k - 1) x + 2k + 2 = 0,当k 时,是一元二次方程.当k 时,是一元一次方程.
≠3
≠±1
=-1
讲授新课
方 程 一般形式 二次项系数 一次项系数 常数项
x(19-2x)=24
x2=2
x2+(x-1 )2 =25
x2-2=0
试一试:
1
0
-2
2x2-19x+24=0
2
-19
24
2x2-2x-24=0
2
-2
-24
讲授新课
4、a为何值时,下列方程为一元二次方程?
(1)ax2-x=2x2
(2) (a-1)x |a|+1 -2x-7=0.
解:(1)将方程式转化为一般形式,得(a-2)x2-x=0,
∴当a-2≠0,即a≠2时,原方程是一元二次方程;
(2)由+1 =2,且a-1≠0得,
当a=-1时,原方程是一元二次方程.
讲授新课
【例2】将方程3x(x-1)=5(x+2)化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数.
解:
去括号,得
3x2-3x=5x+10.
移项、合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
二次项是3x2,系数是3;一次项是-8x,系数是-8;常数项是-10.
讲授新课
1.若关于x的方程(m-2)x2+mx-3=0是一元二次方程,则m的取值范围是( )
A.m≠2 B.m=2 C.m>2 D.m≠0
A
2、如果方程(m-2)xm2-2-mx+3=0是关于x的一元二次方程,那么m的值为_________.
-2
讲授新课
3. 把下列方程化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.
(1) x2-x=2;
(2) 4x+1=x2;
解:(1)将方程化成一般形式,得x2-x-2=0,
二次项系数、一次项系数和常数项分别是1、-1、-2.
(2)将方程转化成一般形式,得x2-4x-1=0,
二次项系数、一次项系数和常数项分别是1、-4、-1.
讲授新课
知识点二 建立一元二次方程的模型
用方程描述下列问题中的数量关系:
(1)一张面积是240 cm2的长方形彩纸,长比宽多8cm,设它的宽为xcm,可得方程_______________.
x(8+x)=240
(2)一枚圆形古钱币的中间是一个边长为1cm 的正方形孔,已知正方形面积是圆面积的 ,设圆的半径为xcm,可得方程___________.
πx2=9
讲授新课
(3)两个连续奇数的积为323,设其中的一个奇数为x,可得方程__________________________.
x(x+2)=323或x(x-2)=323
(4)某工厂经过两年时间将某种产品的产量从每年14 400台提高到16 900台,设平均每年增长的百分率为x,可得方程______________________.
14 400(1+x)2=16 900
讲授新课
典例精析
【例3】观察下面等式:
102 + 112 + 122 = 132 + 142
你还能找到其他的五个连续整数,使前三个数的平方和等于后两个数的平方和吗?
解:如果设五个连续整数中的第一个数为x,那么后面四个数依次可表示为: , , , .
根据题意,可得方程:
x+1
x+2
x+3
x+4
x2 + (x + 1)2 + (x + 2)2 = (x + 3)2 + (x + 4)2.
x2 - 8x - 20=0(一般式).
讲授新课
练一练
解:由勾股定理可知,滑动前梯子底端距墙 m.
如果设梯子底端滑动x m ,那么滑动后梯子底端距墙 m ,
根据题意,可得方程:
1、如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
6
x+6
72 + (x + 6)2 = 102.
x2 + 12 x - 15 = 0(一般式).
10m
8m
1m
xm
当堂检测
1. 下列哪些是一元二次方程?
(1)3x+2=5x-2
(2)x2=0
(3)(x+3)(2x-4)=x2
(4)3y2=(3y+1)(y-2)
(5)x2=x3+x2-1
(6)3x2=5x-1
当堂检测
2.填空:
方程 一般形式 二次项系数 一次项系数 常数项
-2
1
3
1
3
-5
4
0
-5
3
-2
当堂检测
3.将一元二次方程
A. B.
C. D.
C
当堂检测
4. 一元二次方程
A. 2,5,6 B. 5,2,6
C. 2,5,-6 D. 5,2,-6
C
当堂检测
5.已知关于x的一元二次方程(m-3)x2+m2x=9x+5化为一般形式后不含一次项,则m的值为 ( )
A. 0 B. ±3 C. 3 D. -3
D
当堂检测
6.如图,有一面积为600m2的长方形鸡场,鸡场的一边靠墙 (墙长35m) ,另三边用竹篱笆围成,其中一边开有1m的门,竹篱笆的总长为69m.设鸡场垂直于墙的一边为xm,则列方程正确的是( )
A.x(69+1-2x)=600 B.x(69-1-2x)=600
C.x(69-2x)=600 D.x(35+1-2x)=600
A
当堂检测
7. 已知关于x的方程(m-1)+(m-2)x-1=0,回答下面的问题:
(1) 若方程是一元二次方程,求m的值.
解:(1)根据题意,得m2+1=2,且m-1≠0,解得m=-1.
(2)若方程是一元一次方程,则m的值是否存在?若存在,请求出m的值,并求出方程的解.
解:(2) 存在 有两种情况:
① 当满足m2+1=1,且(m-1)+(m-2)≠0时,解得m=0,
则方程变为-3x-1=0,解得x=-;
② 当满足m-1=0,且m-2≠0时,解得m=1,
则方程变为-x-1=0,解得x=-1
课堂小结
一元二次方程
只含有一个未知数x的整式方程,并且都可以
化为ax2+bx+c=0(a,b,c为常数,a≠0)的形式.
概念
一般式:ax2+bx+c=0(a , b , c为常数, a≠0)
ax2 称为二次项,a 称为二次项系数.
bx 称为一次项,b 称为一次项系数.
c 称为常数项.
建立一元二次方程模型
谢 谢~
