鲁教版五四学制:2024-2025年七年级第一学期上册数学1.3探索三角形全等的条件(4)学案和答案
文档属性
| 名称 | 鲁教版五四学制:2024-2025年七年级第一学期上册数学1.3探索三角形全等的条件(4)学案和答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 421.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-15 17:42:08 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024--2025学年度七年级数学上册学案
1.3探索三角形全等的条件(4)
【学习目标】
1.掌握判定三角形全等“边边边”“角角边”“角角边““边角边”的条件并能应用;
2.学会利用全等三角形的方法证明线段(或角)相等.
【自主学习】
预习课本27-28页,思考并完成下列问题.
1. 叫全等三角形.
2.全等三角形的性质:
3.判定三角形全等的方法有: , , 和 .
(
第1题图
)【典型例题】
知识点一 三角形全等判定方法的合理选用
1.如图,M是AB的中点,MC=MD,∠1=∠2,判定△AMC≌△BMD
的方法是 ;若M是AB的中点,∠C=∠D,∠1=∠2,判定
△AMC≌△BMD的方法是 ;若M是AB的中点,∠A=∠B,
∠1=∠2,判定△AMC≌△BMD的方法是
知识点二 三角形全等的应用
2.一块三角形玻璃被小红碰碎成四块,如图,小红只带其中的两块去玻璃店,买了一块和以前一样的玻璃,你认为她带哪两块去玻璃店了( )
A.带其中的任意两块 B.带1,4或3,4就可以了
C.带1,4或2,4就可以了 D.带1,4或2,4或3,4均可
【巩固训练】
1.如图1,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件( )
A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD
2.如图2,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是( )
A.AB∥CD B.AD∥BC C.∠A=∠C D.∠ABC=∠CDA
(
第1题图
第2题图
) (
第1题图
第2题图
)3.如图,CA平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为______.
(
第3题图
)
(
第
4题图
)4.如图,在△ABC中,D、E分别在BC、AC边上。且∠ADE=∠B=∠C,AD=DE
求证:△ADB≌△DEC
(
第4题图
)
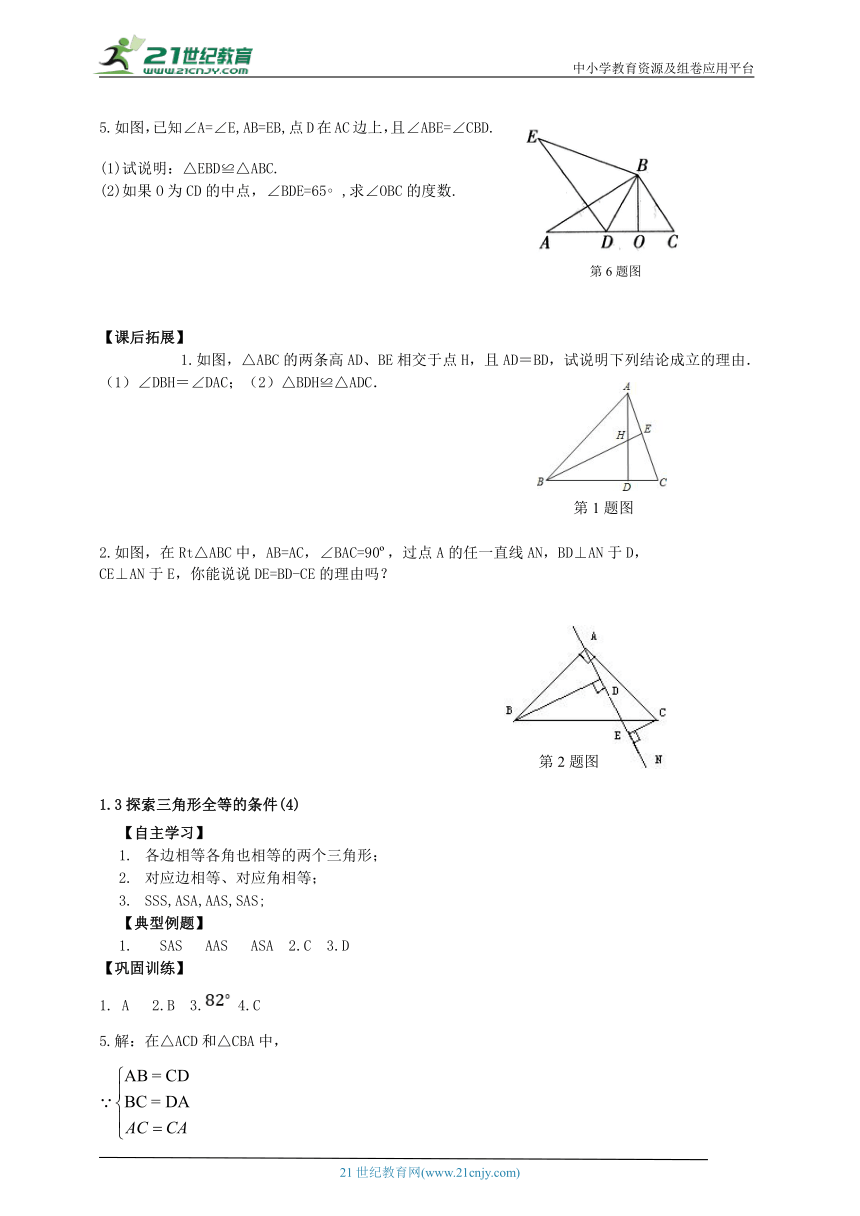
5.如图,已知∠A=∠E,AB=EB,点D在AC边上,且∠ABE=∠CBD.
(1)试说明:△EBD≌△ABC.
(2)如果O为CD的中点,∠BDE=65 ,求∠OBC的度数.
(
第6题图
)
【课后拓展】
1.如图,△ABC的两条高AD、BE相交于点H,且AD=BD,试说明下列结论成立的理由.
(
第1题图
)(1)∠DBH=∠DAC;(2)△BDH≌△ADC.
2.如图,在Rt△ABC中,AB=AC,∠BAC=90 ,过点A的任一直线AN,BD⊥AN于D,
CE⊥AN于E,你能说说DE=BD-CE的理由吗?
(
第2题图
)
1.3探索三角形全等的条件(4)
【自主学习】
各边相等各角也相等的两个三角形;
对应边相等、对应角相等;
SSS,ASA,AAS,SAS;
【典型例题】
SAS AAS ASA 2.C 3.D
【巩固训练】
A 2.B 3. 4.C
5.解:在△ACD和△CBA中,
∴△ACD≌△CAB(SSS)
∴∠CAD=∠ACB,
在△ADE和△BCF中,
∴△ADE≌△CBF(SAS)
∴BF=DE
5.解析(1)证明:
因为 ∠ABE=∠CBD,
所以∠ABE+∠ABD=∠CBD+∠ABD
即∠EBD=∠ABC.
在 △和△中,
所以△EBD≌△ABC(ASA)
因为△EBD≌△ABC,
所以BD=BC,∠BDE=∠C
因为∠BDE=65°,
所以∠65°
因为O为CD的中点,所以DO=CO
在△BOD和△BOC中
所以△BOD≌△BOCOO
所以∠BOD=∠BOC
所以∠BOC=90°
所以∠OBC=180°-∠C-∠BOC=25 °
【课后拓展】
1.证明:(1)∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BEC=90°,
∵∠C=∠C,
∴∠DBH=∠DAC;
(2)∵AD⊥BC
∴∠ADB=∠ADC
在△BDH与△ADC中,
∴△BDH≌△ADC.
解:∵BD⊥AN,CE⊥AN,
∴∠ADB=∠AEC=90 ,
∵∠ABD+∠BAD=90 =∠BAD+∠CAE
∴∠ABD=∠CAE
在△ABD和△CAE中,
∴△ABD=△CAE
∴AD=CE,BD=AE,
∴DE=AE-AD=BD-CE
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024--2025学年度七年级数学上册学案
1.3探索三角形全等的条件(4)
【学习目标】
1.掌握判定三角形全等“边边边”“角角边”“角角边““边角边”的条件并能应用;
2.学会利用全等三角形的方法证明线段(或角)相等.
【自主学习】
预习课本27-28页,思考并完成下列问题.
1. 叫全等三角形.
2.全等三角形的性质:
3.判定三角形全等的方法有: , , 和 .
(
第1题图
)【典型例题】
知识点一 三角形全等判定方法的合理选用
1.如图,M是AB的中点,MC=MD,∠1=∠2,判定△AMC≌△BMD
的方法是 ;若M是AB的中点,∠C=∠D,∠1=∠2,判定
△AMC≌△BMD的方法是 ;若M是AB的中点,∠A=∠B,
∠1=∠2,判定△AMC≌△BMD的方法是
知识点二 三角形全等的应用
2.一块三角形玻璃被小红碰碎成四块,如图,小红只带其中的两块去玻璃店,买了一块和以前一样的玻璃,你认为她带哪两块去玻璃店了( )
A.带其中的任意两块 B.带1,4或3,4就可以了
C.带1,4或2,4就可以了 D.带1,4或2,4或3,4均可
【巩固训练】
1.如图1,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件( )
A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD
2.如图2,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是( )
A.AB∥CD B.AD∥BC C.∠A=∠C D.∠ABC=∠CDA
(
第1题图
第2题图
) (
第1题图
第2题图
)3.如图,CA平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为______.
(
第3题图
)
(
第
4题图
)4.如图,在△ABC中,D、E分别在BC、AC边上。且∠ADE=∠B=∠C,AD=DE
求证:△ADB≌△DEC
(
第4题图
)
5.如图,已知∠A=∠E,AB=EB,点D在AC边上,且∠ABE=∠CBD.
(1)试说明:△EBD≌△ABC.
(2)如果O为CD的中点,∠BDE=65 ,求∠OBC的度数.
(
第6题图
)
【课后拓展】
1.如图,△ABC的两条高AD、BE相交于点H,且AD=BD,试说明下列结论成立的理由.
(
第1题图
)(1)∠DBH=∠DAC;(2)△BDH≌△ADC.
2.如图,在Rt△ABC中,AB=AC,∠BAC=90 ,过点A的任一直线AN,BD⊥AN于D,
CE⊥AN于E,你能说说DE=BD-CE的理由吗?
(
第2题图
)
1.3探索三角形全等的条件(4)
【自主学习】
各边相等各角也相等的两个三角形;
对应边相等、对应角相等;
SSS,ASA,AAS,SAS;
【典型例题】
SAS AAS ASA 2.C 3.D
【巩固训练】
A 2.B 3. 4.C
5.解:在△ACD和△CBA中,
∴△ACD≌△CAB(SSS)
∴∠CAD=∠ACB,
在△ADE和△BCF中,
∴△ADE≌△CBF(SAS)
∴BF=DE
5.解析(1)证明:
因为 ∠ABE=∠CBD,
所以∠ABE+∠ABD=∠CBD+∠ABD
即∠EBD=∠ABC.
在 △和△中,
所以△EBD≌△ABC(ASA)
因为△EBD≌△ABC,
所以BD=BC,∠BDE=∠C
因为∠BDE=65°,
所以∠65°
因为O为CD的中点,所以DO=CO
在△BOD和△BOC中
所以△BOD≌△BOCOO
所以∠BOD=∠BOC
所以∠BOC=90°
所以∠OBC=180°-∠C-∠BOC=25 °
【课后拓展】
1.证明:(1)∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BEC=90°,
∵∠C=∠C,
∴∠DBH=∠DAC;
(2)∵AD⊥BC
∴∠ADB=∠ADC
在△BDH与△ADC中,
∴△BDH≌△ADC.
解:∵BD⊥AN,CE⊥AN,
∴∠ADB=∠AEC=90 ,
∵∠ABD+∠BAD=90 =∠BAD+∠CAE
∴∠ABD=∠CAE
在△ABD和△CAE中,
∴△ABD=△CAE
∴AD=CE,BD=AE,
∴DE=AE-AD=BD-CE
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
