等腰三角形课件
图片预览







文档简介
课件21张PPT。北京五塔寺西安半坡博物馆等腰三角形西演中学 张忠朝学习目标:
1、了解等腰三角形的相关概念,掌握等腰三角形的性质。
2、能运用等腰三角形的性质
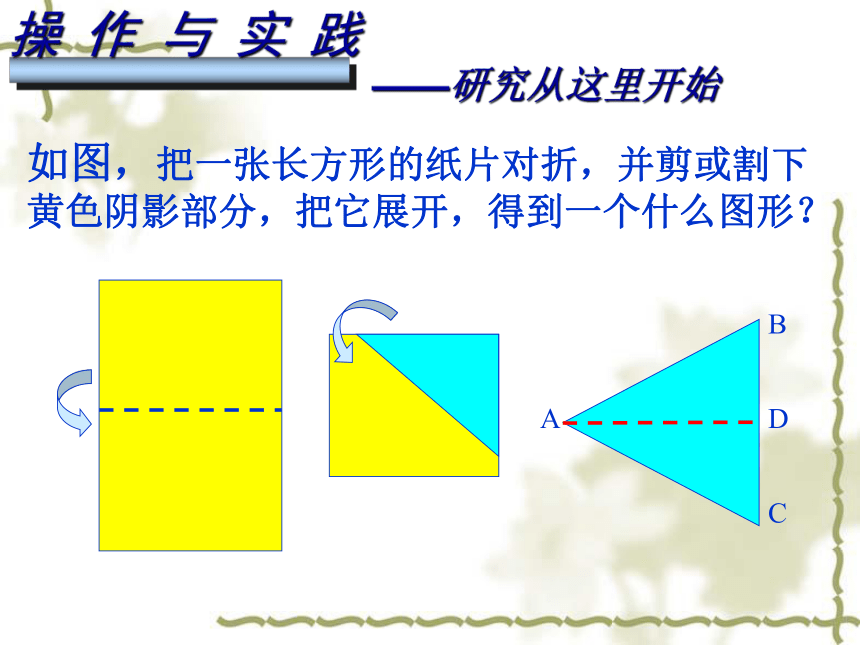
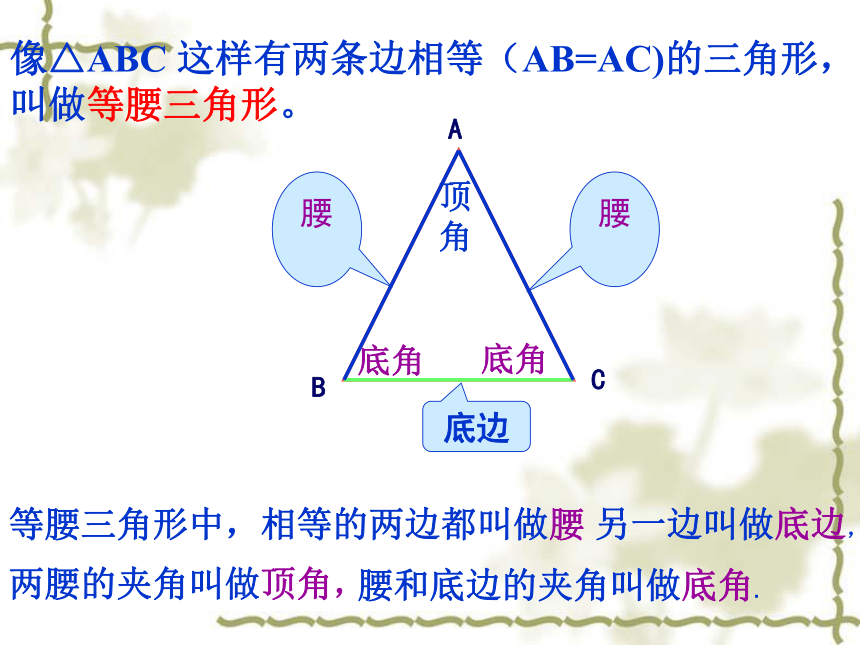
进行证明和计算。? 操 作 与 实 践——研究从这里开始底边底角底角顶角像△ABC 这样有两条边相等(AB=AC)的三角形,
叫做等腰三角形。等腰三角形中,相等的两边都叫做腰另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
1、上面剪出的等腰三角形
是轴对称图形吗?观 察 与 猜 想——问题源于猜想思考2、把剪出的等腰三角形
ABC沿折痕对折,找
出其中重合的角和线段。你能发现等腰三角形的性质吗?说一说你的猜想。性质1 等腰三角形的两个底角相等(等边对等角) 性质2 等腰三角形顶角平分线、底边上的中线、
底边上的高重合 (三线合一) AB、ACAD、ADBD、CD∠BAD 、∠CAD∠C ∠B∠ADC、 ∠ADB你发现什么了?性质1:等腰三角形的两个底角相等——寻找理论的支撑 探 索 与 证 明思考:性质1中的题设和结论
分别是什么?题设: 一个三角形是等腰
三角形结论: 它的两个底角相等思考:怎样用数学符号表示已知和证?已知:在△ABC中,AB=AC
求证: ∠B = ∠CD作△ABC的中线AD,交底边BC于D。探究:已知AB=AC怎样证明∠B = ∠C ?——寻找理论的支撑 探 索 与 证 明D┌作△ABC的高AD,垂直底边BC于D。D12作顶角的平分线AD.已知:如图,△ABC中 AB=AC求证:∠B=∠CD由以上证明过程,你还会得到什么结论?∠BAD=∠CAD ∠ADB=∠ADC=90°以上结论又说明了什么?证明:作底边BC边上的中线AD ∴△ACD≌△ABD(SSS)∴∠B = ∠C 在△BAD和△CAD中(已知)(公共边)(辅助线作法)(全等三角形对应角相等)⒈等腰三角形一个底角为75°,它的另外两个角为_______
⒉等腰三角形一个角为70°,它的另外两个角为___________________
⒊等腰三角形一个角为110°,它的另外两个角为________ 75°30°70°40°或55°55°35°35°巩固练习学以致用——从理论到实践( 1)∵AD⊥BC,
∴∠ BAD = ∠____ CD = ___ (2)∵AD是中线,
∴ AD ⊥___ ,∠BAD =∠____(3)∵AD是角平分线,
∴ AD ⊥___ , BD =___CADBDBCBCCADCD问题:根据等腰三角形性质定理2在△ABC 中, 当AB=AC 时, 学以致用——从理论到实践关于建筑的问题已知:如图,房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC, 求顶架上∠B、∠C、∠BAD、∠CAD的度数.解:在△ABC中,∵AB=AC(已知)∴∠B=∠C(等边对等角)∴∠B=∠C= (180°-∠A=40°(三角形内角和定理)又∵AD⊥BC(已知)∴∠BAD=∠CAD(等腰 三角形顶角的平分线与底边上
的高互相重合)∴∠BAD=∠CAD=50°学以致用——从理论到实践关于撑伞的数学问题已知:如图,AB=AC,DB=DC问:AD与BC有什么关系?猜想:AD垂直平分BC证明:
∵AB=AC,BD=CD,AD=CD∴△ABD≌△ACD(SSS)∴∠BAD=∠CAD∴AD垂直平分BC学以致用——从理论到实践回 顾 与 反 思这节课我们研究了哪些问题?
我们在研究这些问题时,经历了怎样的过程?
通过这个研究过程,你有什么感受和体会? ——让我们的认识升华已有知识作业:
1.必做 习题12.3 第1、4、6题
2.选做 ①习题12.3第8题
②探究得到等腰三角形的其 它方法,思考其中还有那些相等的线段。谢谢大家!
1、了解等腰三角形的相关概念,掌握等腰三角形的性质。
2、能运用等腰三角形的性质
进行证明和计算。? 操 作 与 实 践——研究从这里开始底边底角底角顶角像△ABC 这样有两条边相等(AB=AC)的三角形,
叫做等腰三角形。等腰三角形中,相等的两边都叫做腰另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
1、上面剪出的等腰三角形
是轴对称图形吗?观 察 与 猜 想——问题源于猜想思考2、把剪出的等腰三角形
ABC沿折痕对折,找
出其中重合的角和线段。你能发现等腰三角形的性质吗?说一说你的猜想。性质1 等腰三角形的两个底角相等(等边对等角) 性质2 等腰三角形顶角平分线、底边上的中线、
底边上的高重合 (三线合一) AB、ACAD、ADBD、CD∠BAD 、∠CAD∠C ∠B∠ADC、 ∠ADB你发现什么了?性质1:等腰三角形的两个底角相等——寻找理论的支撑 探 索 与 证 明思考:性质1中的题设和结论
分别是什么?题设: 一个三角形是等腰
三角形结论: 它的两个底角相等思考:怎样用数学符号表示已知和证?已知:在△ABC中,AB=AC
求证: ∠B = ∠CD作△ABC的中线AD,交底边BC于D。探究:已知AB=AC怎样证明∠B = ∠C ?——寻找理论的支撑 探 索 与 证 明D┌作△ABC的高AD,垂直底边BC于D。D12作顶角的平分线AD.已知:如图,△ABC中 AB=AC求证:∠B=∠CD由以上证明过程,你还会得到什么结论?∠BAD=∠CAD ∠ADB=∠ADC=90°以上结论又说明了什么?证明:作底边BC边上的中线AD ∴△ACD≌△ABD(SSS)∴∠B = ∠C 在△BAD和△CAD中(已知)(公共边)(辅助线作法)(全等三角形对应角相等)⒈等腰三角形一个底角为75°,它的另外两个角为_______
⒉等腰三角形一个角为70°,它的另外两个角为___________________
⒊等腰三角形一个角为110°,它的另外两个角为________ 75°30°70°40°或55°55°35°35°巩固练习学以致用——从理论到实践( 1)∵AD⊥BC,
∴∠ BAD = ∠____ CD = ___ (2)∵AD是中线,
∴ AD ⊥___ ,∠BAD =∠____(3)∵AD是角平分线,
∴ AD ⊥___ , BD =___CADBDBCBCCADCD问题:根据等腰三角形性质定理2在△ABC 中, 当AB=AC 时, 学以致用——从理论到实践关于建筑的问题已知:如图,房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC, 求顶架上∠B、∠C、∠BAD、∠CAD的度数.解:在△ABC中,∵AB=AC(已知)∴∠B=∠C(等边对等角)∴∠B=∠C= (180°-∠A=40°(三角形内角和定理)又∵AD⊥BC(已知)∴∠BAD=∠CAD(等腰 三角形顶角的平分线与底边上
的高互相重合)∴∠BAD=∠CAD=50°学以致用——从理论到实践关于撑伞的数学问题已知:如图,AB=AC,DB=DC问:AD与BC有什么关系?猜想:AD垂直平分BC证明:
∵AB=AC,BD=CD,AD=CD∴△ABD≌△ACD(SSS)∴∠BAD=∠CAD∴AD垂直平分BC学以致用——从理论到实践回 顾 与 反 思这节课我们研究了哪些问题?
我们在研究这些问题时,经历了怎样的过程?
通过这个研究过程,你有什么感受和体会? ——让我们的认识升华已有知识作业:
1.必做 习题12.3 第1、4、6题
2.选做 ①习题12.3第8题
②探究得到等腰三角形的其 它方法,思考其中还有那些相等的线段。谢谢大家!
