初中数学人教版十一章-十三章 单元测试(含答案)
文档属性
| 名称 | 初中数学人教版十一章-十三章 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 676.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-14 16:47:22 | ||
图片预览

文档简介
初中数学人教版十一章-十三章
一、单选题
1.一个n边形的每个外角都是45°,则这个n边形的内角和是( )
A.1080° B.540° C.2700° D.2160°
2.如图,点、、、在同一条直线上,且,下列判断错误的是 ( )
A. B. C. D.
3.如果一个正多边形的一个外角是,则这个正多边形是正( )边形
A.六 B.八 C.十 D.十二
4.如图,在中,,,的中垂线交于点D,交于点E,下述结论中正确的是( )
A.点D是线段的中点 B.
C.的周长等于 D.平分
5.如图,将纸片绕点C顺时针旋转得到,连接,若,则的度数为( )
A. B. C. D.
6.、、是某三角形三边的长,则等于( )
A. B. C. D.
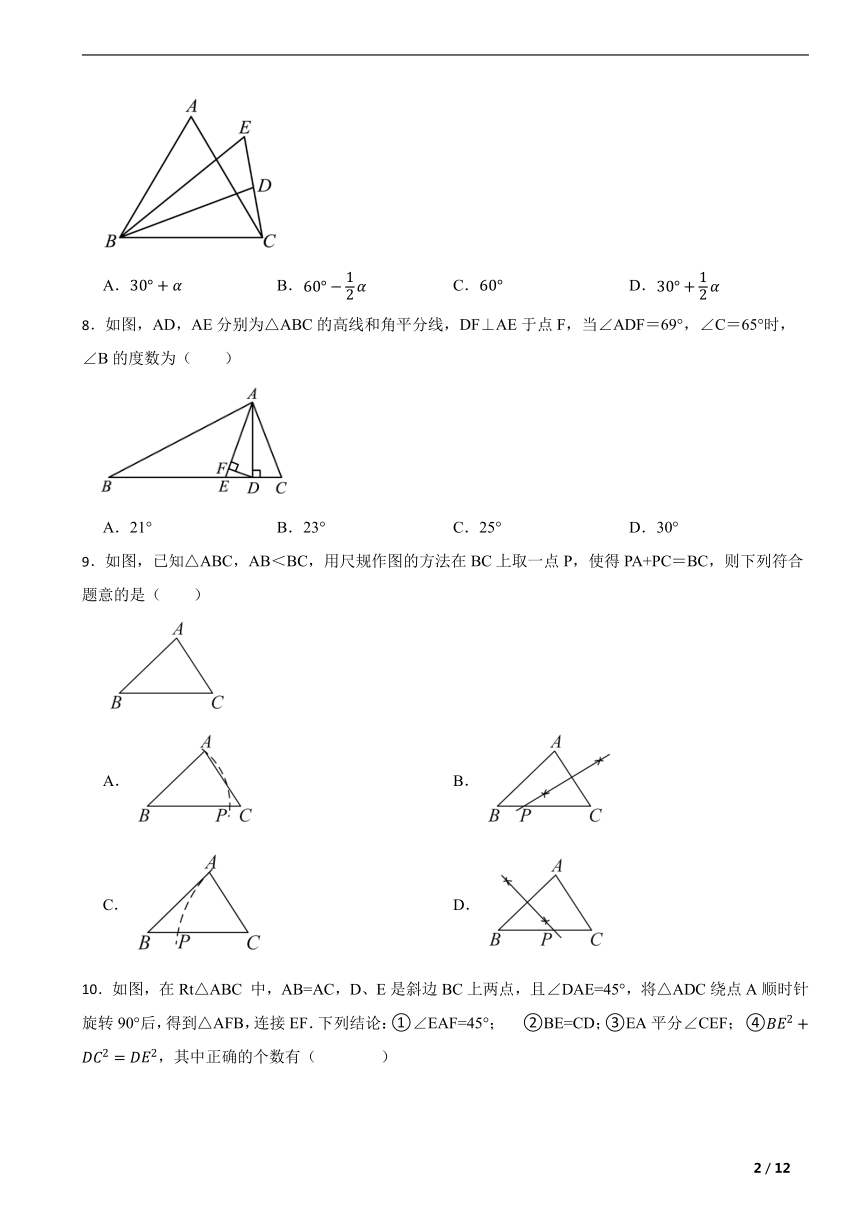
7.如图,在等边中,点在边上方,满足,的角平分线交的延长线于点,若,则的度数为( )
A. B. C. D.
8.如图,AD,AE分别为△ABC的高线和角平分线,DF⊥AE于点F,当∠ADF=69°,∠C=65°时,∠B的度数为( )
A.21° B.23° C.25° D.30°
9.如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列符合题意的是( )
A. B.
C. D.
10.如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF.下列结论:①∠EAF=45°; ②BE=CD;③EA平分∠CEF; ④,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
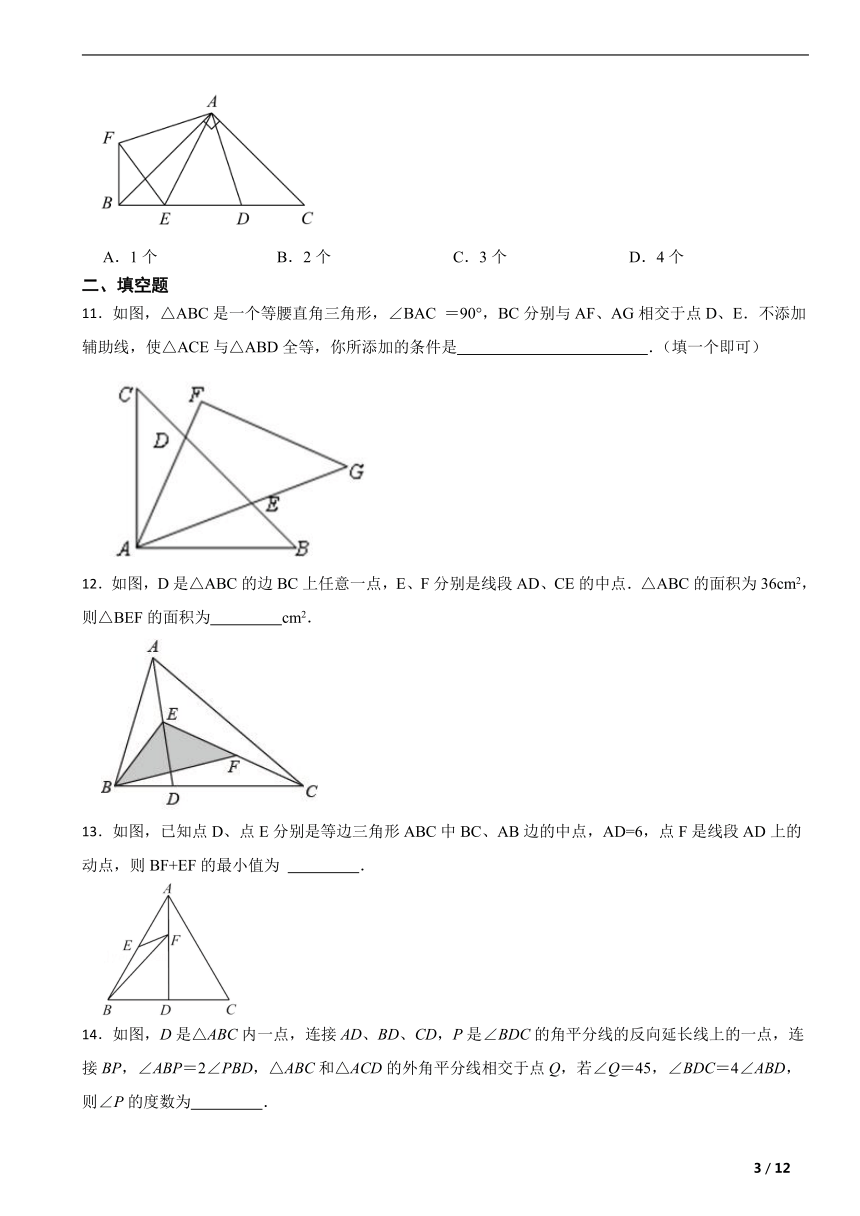
11.如图,△ABC是一个等腰直角三角形,∠BAC =90°,BC分别与AF、AG相交于点D、E.不添加辅助线,使△ACE与△ABD全等,你所添加的条件是 .(填一个即可)
12.如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点.△ABC的面积为36cm2,则△BEF的面积为 cm2.
13.如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=6,点F是线段AD上的动点,则BF+EF的最小值为 .
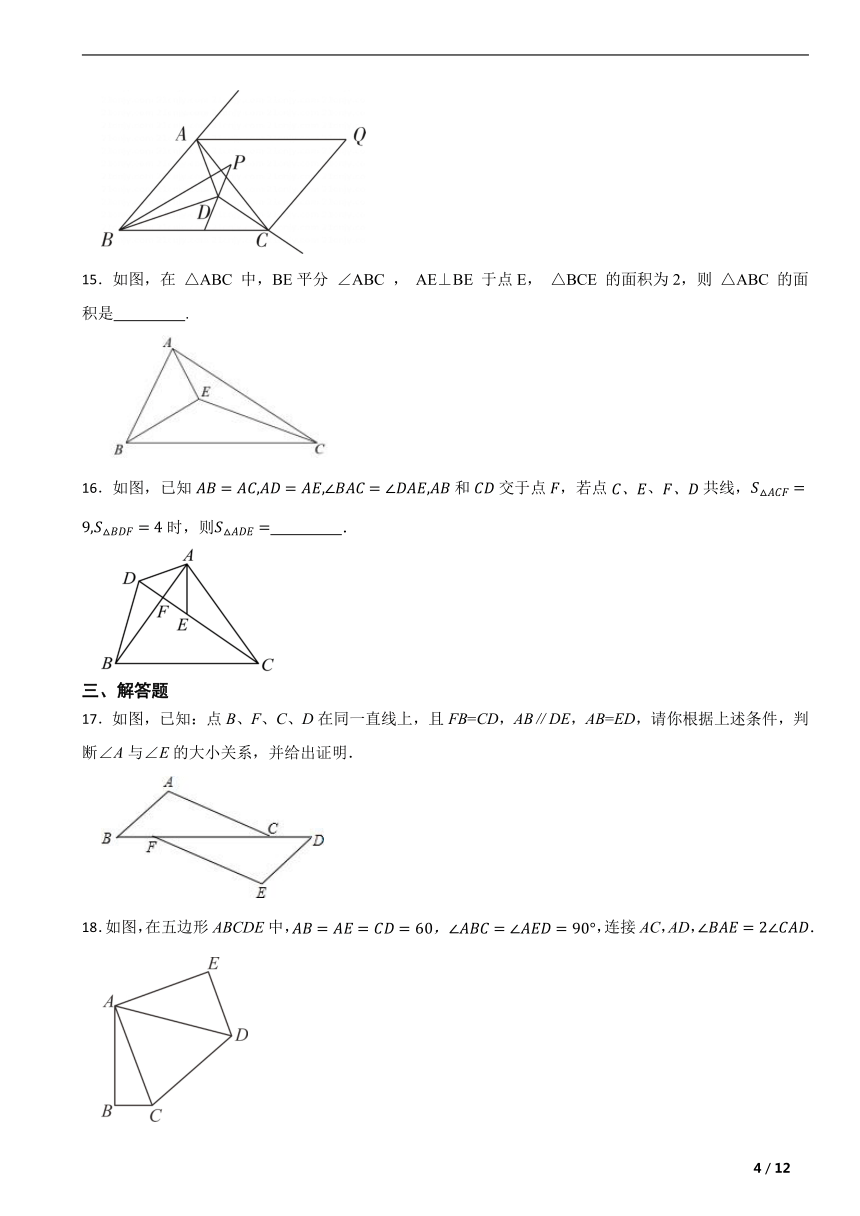
14.如图,D是△ABC内一点,连接AD、BD、CD,P是∠BDC的角平分线的反向延长线上的一点,连接BP,∠ABP=2∠PBD,△ABC和△ACD的外角平分线相交于点Q,若∠Q=45,∠BDC=4∠ABD,则∠P的度数为 .
15.如图,在 △ABC 中,BE平分 ∠ABC , AE⊥BE 于点E, △BCE 的面积为2,则 △ABC 的面积是 .
16.如图,已知和交于点,若点、共线,时,则 .
三、解答题
17.如图,已知:点B、F、C、D在同一直线上,且FB=CD,AB∥DE,AB=ED,请你根据上述条件,判断∠A与∠E的大小关系,并给出证明.
18.如图,在五边形ABCDE中,,连接AC,AD,.
(1)已知,则 .
(2)求五边形ABCDE的周长.
【注:五边形的周长指组成五边形的所有边的和】
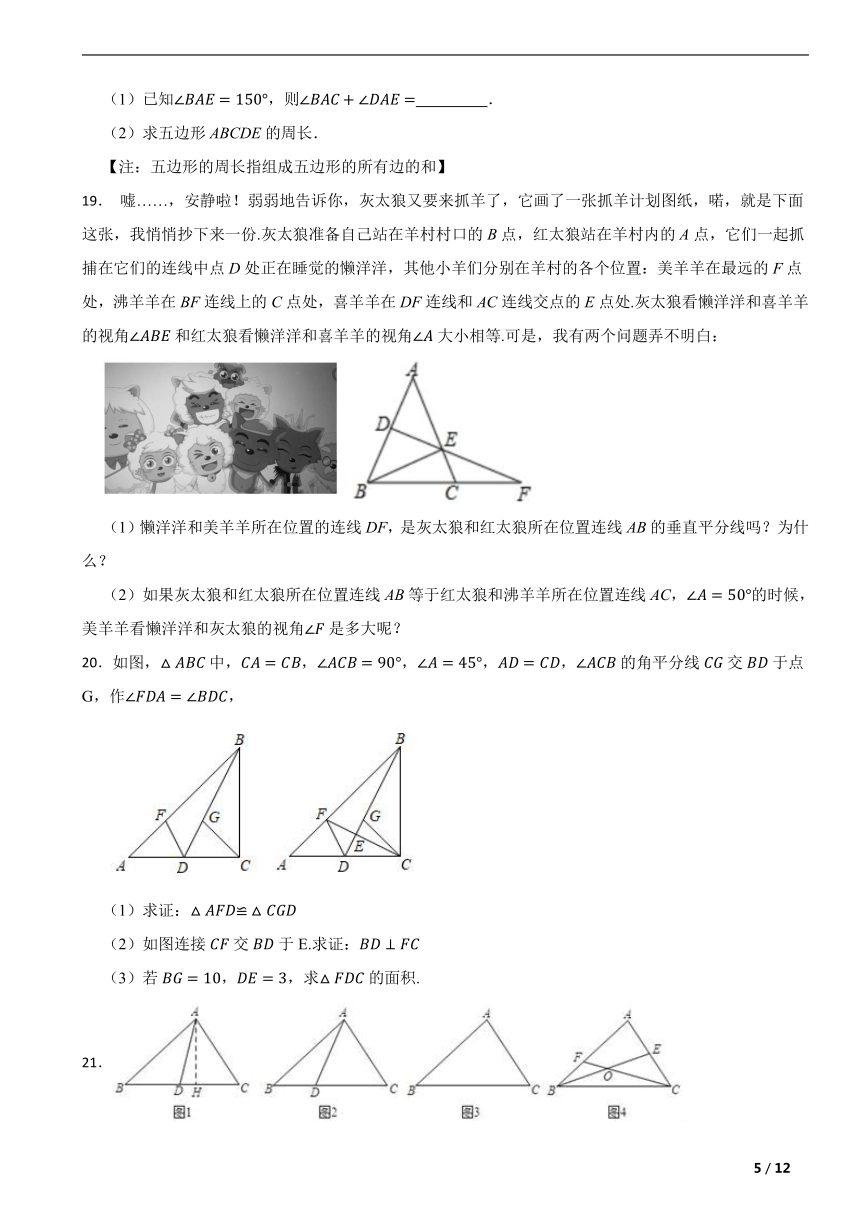
19. 嘘……,安静啦!弱弱地告诉你,灰太狼又要来抓羊了,它画了一张抓羊计划图纸,喏,就是下面这张,我悄悄抄下来一份.灰太狼准备自己站在羊村村口的B点,红太狼站在羊村内的A点,它们一起抓捕在它们的连线中点D处正在睡觉的懒洋洋,其他小羊们分别在羊村的各个位置:美羊羊在最远的F点处,沸羊羊在BF连线上的C点处,喜羊羊在DF连线和AC连线交点的E点处.灰太狼看懒洋洋和喜羊羊的视角和红太狼看懒洋洋和喜羊羊的视角大小相等.可是,我有两个问题弄不明白:
(1)懒洋洋和美羊羊所在位置的连线DF,是灰太狼和红太狼所在位置连线AB的垂直平分线吗?为什么?
(2)如果灰太狼和红太狼所在位置连线AB等于红太狼和沸羊羊所在位置连线AC,的时候,美羊羊看懒洋洋和灰太狼的视角是多大呢?
20.如图,中,,,,,的角平分线交于点G,作,
(1)求证:
(2)如图连接交于E.求证:
(3)若,,求的面积.
21.
(1)(阅读理解)
如图(1),AD是△ABC的中线,作△ABC的高AH.
∵AD是△ABC的中线
∴BD=CD
∵S△ABD= BD AH,S△ACD= CD AH
∴S△ABD S△ACD(填:<或>或=)
(2)(结论拓展)
△ABC中,D是BC边上一点,若 ,则 =
(3)(结论应用)
如图(3),请你将△ABC分成4个面积相等的三角形(画出分割线即可)
如图(4),BE是△ABC的中线,F是AB边上一点,连接CF交BE于点O,若 ,则 的值是多少.说明你的理由
22.如图,在△ABC中,AB=BC,∠ABC=90°,D是边AC上一点,连接DB,过点C作CE⊥BD交BD于点E.
(1)如图1,若∠DBC=4∠DCE,求∠DCE的度数;
(2)如图2,在EC上截取EF=EB.连接AF交BD于点G,求证:CF=2EG;
(3)如图3,若, 点D为线段AC上一点,点M是直线BC上一动点,连接MD,将线段MD绕点D顺时针旋转90°得到线段M′D,点P是线段BC的中点,点Q是线段BD上一个动点,连接PQ,M′Q,当PQ+M′Q最小时,请直接写PQ的长度.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】D
10.【答案】C
11.【答案】CD=BE(答案不唯一)
12.【答案】9
13.【答案】6
14.【答案】50
15.【答案】4
16.【答案】5
17.【答案】解:结论:∠A=∠E.
理由:∵AB∥DE,
∴∠B=∠D,
∵BF=CD,
∴BC=DF,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SAS),
∴∠A=∠E
18.【答案】(1)75°
(2)解:将△ABC绕点A逆时针旋转,使点B与点E重合,点C落在点F处;
∴AF=AC,∠B=∠AEF=90°,∠BAC=∠EAF,BC=EF
∵∠AED=90°,∴∠AEF+∠AED=180°,
∴D、E、F在同一条直线上,
∵∠BAE=∠BAC+∠CAD+ ∠DAE=2∠CAD.∴∠BAC+∠DAE=∠CAD
∴∠EAF+∠DAE=∠CAD
∴∠DAF=∠CAD
∵AD=AD,∴△CAD≌△FAD,
∴DF=CD,∵DF=DE+EF,∴CD=DE+BC
∴五边形ABCDE的周长=AB+BC+CD+DE+AE=4AB=240
19.【答案】(1)解:是,理由:因为,所以,
因为D是AB中点,所以,
所以ED是AB的垂直平分线,
由题分析可知D,E,F在同一直线上,即可证明.
(2)解:
20.【答案】(1)证明:∵,的角平分线交于点G,,
∴,
在和中,
,
∴;
(2)证明:∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∴;
(3)解:∵,,
∴,
∵,,
∴.
21.【答案】(1)=
(2)
(3)解:如下图:
将△ABC的面积四等分的方法如图所示,(方法见图中说明)
如图4,结论: =3;
理由是:如图4,连接AO,
∵BE是△ABC的中线,
∴S△ABE=S△CBE,S△AOE=S△COE,
∴S△ABO=S△CBO,
∵ ,
∴ ,
设S△BFO=x,则S△AFO=2x,S△CBO=3x,
,
.
故答案为3.
22.【答案】(1)解:∵AB=BC,∠ABC=90°,
∴∠A=∠ACB=45°,
设∠DCE=α,则∠DBC=4α, ∠BCE=∠ACB-∠DCE=45°-α,
∵CE⊥BD,
∴∠BEC=∠BED=90°,
∴∠DBC+∠BCE=90°,
∴45°-α+4α=90°,
∴α=15°,
∴∠BCE=45°-α=30°,
∴∠DCE=45°-30°=15°;
(2)证明:方法一:如图,
作AH⊥BD,交BD的延长线于点H,
∴∠H=∠BEC=90°,
∴∠BCE+∠CBE=90°,
∵∠ABC=90°,
∴∠ABH+∠CBE=90°,
∴∠BCE=∠ABH,
∵AB=BC,
∴△ABH≌△BCE(AAS),
∴BE=AH,BH=CF,
∵EF=EB,
∴AH=EF,
∵∠H=∠FEG=90°,∠AGH=∠FGE,
∴△AGH≌△FGE(AAS),
∴GH=GE,
∴EH=2EG,
∵BH=CE,BE=EF,
∴CF=EH=2EG,
方法二:如图,
连接BF,延长FE至H,连接AH, BH,
∵CE⊥BD,
∴BH=BF,
∴∠BFE=∠BHF,
∵BE=EF,∠CEB=90°,
∴∠BFE=∠EBF=45°,
∴∠HBF=90°,
∴∠HBF=∠ABC=90°,
∴∠ABH=∠BCF,
∵AB=BC,
∴△ABH≌△CBF(SAS),
∴AH=CF,∠AHB=∠CBF=180°-∠BFE=135°,
∴∠AHF=∠AHB-∠BHF=135°-45°=90°,
∴∠AHF=∠CED=90°,
∴EG∥AH,
∴AH=2EG,
∴CF=2EG;
(3)解:
1 / 1
一、单选题
1.一个n边形的每个外角都是45°,则这个n边形的内角和是( )
A.1080° B.540° C.2700° D.2160°
2.如图,点、、、在同一条直线上,且,下列判断错误的是 ( )
A. B. C. D.
3.如果一个正多边形的一个外角是,则这个正多边形是正( )边形
A.六 B.八 C.十 D.十二
4.如图,在中,,,的中垂线交于点D,交于点E,下述结论中正确的是( )
A.点D是线段的中点 B.
C.的周长等于 D.平分
5.如图,将纸片绕点C顺时针旋转得到,连接,若,则的度数为( )
A. B. C. D.
6.、、是某三角形三边的长,则等于( )
A. B. C. D.
7.如图,在等边中,点在边上方,满足,的角平分线交的延长线于点,若,则的度数为( )
A. B. C. D.
8.如图,AD,AE分别为△ABC的高线和角平分线,DF⊥AE于点F,当∠ADF=69°,∠C=65°时,∠B的度数为( )
A.21° B.23° C.25° D.30°
9.如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列符合题意的是( )
A. B.
C. D.
10.如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF.下列结论:①∠EAF=45°; ②BE=CD;③EA平分∠CEF; ④,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,△ABC是一个等腰直角三角形,∠BAC =90°,BC分别与AF、AG相交于点D、E.不添加辅助线,使△ACE与△ABD全等,你所添加的条件是 .(填一个即可)
12.如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点.△ABC的面积为36cm2,则△BEF的面积为 cm2.
13.如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=6,点F是线段AD上的动点,则BF+EF的最小值为 .
14.如图,D是△ABC内一点,连接AD、BD、CD,P是∠BDC的角平分线的反向延长线上的一点,连接BP,∠ABP=2∠PBD,△ABC和△ACD的外角平分线相交于点Q,若∠Q=45,∠BDC=4∠ABD,则∠P的度数为 .
15.如图,在 △ABC 中,BE平分 ∠ABC , AE⊥BE 于点E, △BCE 的面积为2,则 △ABC 的面积是 .
16.如图,已知和交于点,若点、共线,时,则 .
三、解答题
17.如图,已知:点B、F、C、D在同一直线上,且FB=CD,AB∥DE,AB=ED,请你根据上述条件,判断∠A与∠E的大小关系,并给出证明.
18.如图,在五边形ABCDE中,,连接AC,AD,.
(1)已知,则 .
(2)求五边形ABCDE的周长.
【注:五边形的周长指组成五边形的所有边的和】
19. 嘘……,安静啦!弱弱地告诉你,灰太狼又要来抓羊了,它画了一张抓羊计划图纸,喏,就是下面这张,我悄悄抄下来一份.灰太狼准备自己站在羊村村口的B点,红太狼站在羊村内的A点,它们一起抓捕在它们的连线中点D处正在睡觉的懒洋洋,其他小羊们分别在羊村的各个位置:美羊羊在最远的F点处,沸羊羊在BF连线上的C点处,喜羊羊在DF连线和AC连线交点的E点处.灰太狼看懒洋洋和喜羊羊的视角和红太狼看懒洋洋和喜羊羊的视角大小相等.可是,我有两个问题弄不明白:
(1)懒洋洋和美羊羊所在位置的连线DF,是灰太狼和红太狼所在位置连线AB的垂直平分线吗?为什么?
(2)如果灰太狼和红太狼所在位置连线AB等于红太狼和沸羊羊所在位置连线AC,的时候,美羊羊看懒洋洋和灰太狼的视角是多大呢?
20.如图,中,,,,,的角平分线交于点G,作,
(1)求证:
(2)如图连接交于E.求证:
(3)若,,求的面积.
21.
(1)(阅读理解)
如图(1),AD是△ABC的中线,作△ABC的高AH.
∵AD是△ABC的中线
∴BD=CD
∵S△ABD= BD AH,S△ACD= CD AH
∴S△ABD S△ACD(填:<或>或=)
(2)(结论拓展)
△ABC中,D是BC边上一点,若 ,则 =
(3)(结论应用)
如图(3),请你将△ABC分成4个面积相等的三角形(画出分割线即可)
如图(4),BE是△ABC的中线,F是AB边上一点,连接CF交BE于点O,若 ,则 的值是多少.说明你的理由
22.如图,在△ABC中,AB=BC,∠ABC=90°,D是边AC上一点,连接DB,过点C作CE⊥BD交BD于点E.
(1)如图1,若∠DBC=4∠DCE,求∠DCE的度数;
(2)如图2,在EC上截取EF=EB.连接AF交BD于点G,求证:CF=2EG;
(3)如图3,若, 点D为线段AC上一点,点M是直线BC上一动点,连接MD,将线段MD绕点D顺时针旋转90°得到线段M′D,点P是线段BC的中点,点Q是线段BD上一个动点,连接PQ,M′Q,当PQ+M′Q最小时,请直接写PQ的长度.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】D
10.【答案】C
11.【答案】CD=BE(答案不唯一)
12.【答案】9
13.【答案】6
14.【答案】50
15.【答案】4
16.【答案】5
17.【答案】解:结论:∠A=∠E.
理由:∵AB∥DE,
∴∠B=∠D,
∵BF=CD,
∴BC=DF,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SAS),
∴∠A=∠E
18.【答案】(1)75°
(2)解:将△ABC绕点A逆时针旋转,使点B与点E重合,点C落在点F处;
∴AF=AC,∠B=∠AEF=90°,∠BAC=∠EAF,BC=EF
∵∠AED=90°,∴∠AEF+∠AED=180°,
∴D、E、F在同一条直线上,
∵∠BAE=∠BAC+∠CAD+ ∠DAE=2∠CAD.∴∠BAC+∠DAE=∠CAD
∴∠EAF+∠DAE=∠CAD
∴∠DAF=∠CAD
∵AD=AD,∴△CAD≌△FAD,
∴DF=CD,∵DF=DE+EF,∴CD=DE+BC
∴五边形ABCDE的周长=AB+BC+CD+DE+AE=4AB=240
19.【答案】(1)解:是,理由:因为,所以,
因为D是AB中点,所以,
所以ED是AB的垂直平分线,
由题分析可知D,E,F在同一直线上,即可证明.
(2)解:
20.【答案】(1)证明:∵,的角平分线交于点G,,
∴,
在和中,
,
∴;
(2)证明:∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∴;
(3)解:∵,,
∴,
∵,,
∴.
21.【答案】(1)=
(2)
(3)解:如下图:
将△ABC的面积四等分的方法如图所示,(方法见图中说明)
如图4,结论: =3;
理由是:如图4,连接AO,
∵BE是△ABC的中线,
∴S△ABE=S△CBE,S△AOE=S△COE,
∴S△ABO=S△CBO,
∵ ,
∴ ,
设S△BFO=x,则S△AFO=2x,S△CBO=3x,
,
.
故答案为3.
22.【答案】(1)解:∵AB=BC,∠ABC=90°,
∴∠A=∠ACB=45°,
设∠DCE=α,则∠DBC=4α, ∠BCE=∠ACB-∠DCE=45°-α,
∵CE⊥BD,
∴∠BEC=∠BED=90°,
∴∠DBC+∠BCE=90°,
∴45°-α+4α=90°,
∴α=15°,
∴∠BCE=45°-α=30°,
∴∠DCE=45°-30°=15°;
(2)证明:方法一:如图,
作AH⊥BD,交BD的延长线于点H,
∴∠H=∠BEC=90°,
∴∠BCE+∠CBE=90°,
∵∠ABC=90°,
∴∠ABH+∠CBE=90°,
∴∠BCE=∠ABH,
∵AB=BC,
∴△ABH≌△BCE(AAS),
∴BE=AH,BH=CF,
∵EF=EB,
∴AH=EF,
∵∠H=∠FEG=90°,∠AGH=∠FGE,
∴△AGH≌△FGE(AAS),
∴GH=GE,
∴EH=2EG,
∵BH=CE,BE=EF,
∴CF=EH=2EG,
方法二:如图,
连接BF,延长FE至H,连接AH, BH,
∵CE⊥BD,
∴BH=BF,
∴∠BFE=∠BHF,
∵BE=EF,∠CEB=90°,
∴∠BFE=∠EBF=45°,
∴∠HBF=90°,
∴∠HBF=∠ABC=90°,
∴∠ABH=∠BCF,
∵AB=BC,
∴△ABH≌△CBF(SAS),
∴AH=CF,∠AHB=∠CBF=180°-∠BFE=135°,
∴∠AHF=∠AHB-∠BHF=135°-45°=90°,
∴∠AHF=∠CED=90°,
∴EG∥AH,
∴AH=2EG,
∴CF=2EG;
(3)解:
1 / 1
